Дерево Фенвика. Дерево отрезков и динамическое программирование для RMQ.

Дерево фенвика

На практике часто возникают задачи, в которых приходится работать с динамически изменяющимися данными. Дерево Фенвика является структурой данных, позволяющей достаточно эффективно выдавать ответы на запросы о частичных суммах на различных отрезках массива,

элементы которого могут меняться в процессе работы.

Пусть задан массив A из N чисел: A0, A1,..., AN−1. Дерево Фенвика — это структура данных, позволяющая выполнять две операции:

• rsq(i, j) — выдать сумму элементов массива A с i-го по j-й вклю-

чительно (rsq является сокращением от range sum query);

• update(k, d) — прибавить к k-му элементу массива A некоторое

число d.

Дерево Фенвика позволяет существенно сократить это время, поскольку выполняет каждую из указанных операций за время O(log N).

Описание структуры

На практике дерево Фенвика представляет собой массив B из N чисел: B0, B1,..., BN−1, в k-м элементекоторого хранится сумма элементов массива A с f(k)-го по k-й: Bk = сумма от f(k) до kиз A_i, где f(k) = k&(k + 1). Под & имеется ввиду операция побитового И.

Рассмотрим двоичное представление

k... 0111... 1

k+1... 1000... 0

&&

f(k)... 0000... 0

 

Рассмотрим, как с помощью дерева Фенвика реализуются операции ответа на запрос rsq(i, j) о частичной сумме элементов массива A с i-го по j-й и запрос update(k, d) прибавления к k-му элементу массива A числа d.

 

Ответ на запрос о частичной сумме элементов массива A rsq(i, j)

Заметим, что rsq(i, j) = rsq(0, j) − rsq(0, i − 1) (для i = 0 положим rsq(0, −1) = 0). Таким образом, для ответа на запрос rsq(i, j) достаточно научиться отвечать на запрос вида rsq(0, k), который для краткости обозначим rsq(k). Ответ на запрос rsq(k) вычисляется следующим образом:

rsq(k) = Bk + Bf(k)−1 + Bf(f(k)−1)−1 +... + Bf(f(...f(k)−1...)−1)−1 (1)

Перепишем эту формулу в виде

rsq(k) = Bk0+ Bk1+ Bk2 +... + Bkn— суммирование начинается с Bk, а индекс каждого следующего слагаемого получается из индекса предыдущего по формуле:

k_i+1 = f(k_i) − 1 = (k_i&(k_i + 1)) − 1, г де k₀ = k. Суммирование заканчи-

вается, когда ki становится меньше 0, то есть k_m+1 = f(k_m) − 1 < 0. Та-

кой момент наступает, поскольку каждый следующий индекс строго меньше предыдущего.

 

k0 14 11102

f(k0) 14 11102

k1 13 11012

f(k1) 12 11002

k2 11 10012

f(k2) 8 10002

k3 7 01112

f(k3) 0 0002

 

Количество слагаемых равно количеству единичных битов в числе f(k) плюс один. Переход к каждому следующему индексу «выбивает» ровно по одному единичному биту из числа f(ki). А поскольку в худшем случае количество единичных бит в f(k) может быть порядкаO(log N), то и ответ на запрос rsq(k) в худшем случае требует порядкаO(log N) времени.

 

Изменение k-го элемента массива A — update(k, d)

При изменении k-г оэлемента массива A необходимо соответствующим образом изменить элементы массива B, в определении которых частичные суммы содержат элемент Ak. То есть для выполнения операцииupdate(k, d) (прибавления к k-му элементу массива A числа d) нужно прибавить d к тем элементам Bj массива B, для которых f(j) <= k <=j (т.е. те элементы массива B, где лежит значение A[k]). Утверждается, что все такие j, и только они, являются элементами последовательности k0, k1, k2,..., km, где k0 = k, ki+1 = ki |(ki + 1), km+1 = km |(km + 1) > N − 1. Под | имеется в виду операция побитового ИЛИ.

Сначала покажем, что указанная

k_i... 0111... 1

k_i+1... 1000... 0

| |

k_i+1... 1111... 1

последовательность строго возрастает, и ее длина составляет порядка O(log N) в худшем случае. Для этого рассмотрим двоичное представление числа ki. Число ki+1 получается из ki заменой младшего нулевого бита на единичный. Таким образом, ki+1 > ki, а длина последовательности m заведомо не превосходит количества бит в двоичном представлении числа N.

 

В силу того, что длина последовательности ki составляет O(log N) в худшем случае, время работы процедуры update(k, d), составляет O(log N).

 

Дерево отрезков

Эта структура весьма полезна в случаях, когда необходимо часто искать значение какой-то функции на отрезках линейного массива и иметь возможность быстро изменять значения группы подряд идущих элементов.
Типичный пример задачи на дерево отрезков:
Есть линейный массив, изначально заполненный некоторыми данными. Далее приходят 2 типа запросов:
1й тип — найти значение максимального элемента на отрезке массива [a..b].
2й тип — заменить iй элемент массива на x.
Возможен запрос «добавить х ко всем элементам на отрезке [a..b]», но в данной статье я его не рассматриваю.
С помощью дерева отрезков можно искать не только максимум чисел, но и любую функцию, удовлетворяющую свойству ассоциативности.

Это ограничение связано с тем, что используется предпросчет значений для некоторых отрезков.
Так же можно искать, например, не значения, а порядковые номера элементов.
Желательно, что бы функция имела «нейтральный» аргумент, который не оказывает влияния на результат. Например, для суммы это число 0: (a + 0 = a), а для максимума это бесконечность: max(a, -inf) = a.
Итак, поехали.
Самый простой (и медленный) способ решать представленную выше задачу, это завести линейный массив, и покорно делать то, что от нас хотят.
при такой реализации время нахождения ответа на запрос имеет порядок О(n). в среднем, придется пройтись по половине массива что бы найти максимум. Хотя есть и положительные моменты — изменение значения какого-либо элемента требует O(1) времени. Этот алгоритм можно ускорить в 2 раза, если выполнить небольшой предпросчет: для каждой пары элементов найдем значение максимального из них, и запишем в другой массив. Тогда при поиске максимума на отрезке, для каждой пары элементов уже известно значение большего, и сравнивать придется только с ним.остается только аккуратно проверить граничные элементы, так как граница запрашиваемого отрезка не обязательно четная.
Понятно, что над этими массивами можно ввести еще один, что бы поиск был еще в 2 раза быстрее, а над ним еще один… и так до тех пор, пока самый верхний массив не будет состоять из одного элемента. Как не трудно догадаться, значение единственного элемента в самом верхнем массиве – это значение максимального элемента.

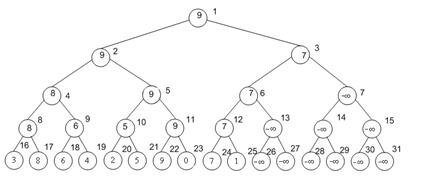
Некоторые пояснения: число рядом с вершиной дерева — это положение этой вершины в реальном массиве. При такой реализации хранения дерева очень удобно искать предка и потомков вершины: предок вершины i имеет номер i/2, а потомки номера i*2 и i*2+1. Из рисунка видно, что необходимо, что бы длинна массива была степенью двойки. Если это не так, то массив можно в конце дополнить нейтральными элементами. Расход памяти на хранение структуры от 2n до 4n, (n — количество элементов).
Алгоритм поиска «сверху» (есть еще и «снизу») весьма прост и в понимании и в реализации (хотя тех, кто не знаком с рекурсией, это всё может озадачить).
Алгоритм таков:
Начинаем опрос с вершины 1 (самая верхняя).
1.пусть текущая вершина знает максимум на промежутке l..r.
«пересекаются области [a..b] и [l..r]?»
возможные варианты:
a. вообще не пересекаются.
что бы не влиять на результат вычисления, вернем нейтральный элемент (-бесконечность).
b. область [l..r] полностью лежит внутри [a..b].
вернуть предпросчитанное значение в текущей вершине.
с. другой вариант перекрытия областей.
спросить то же самое у детей текущей вершины и вычислить максимум среди них (смотрите код, если непонятно).
Как видно, алгоритм короткий, но рекурсивный. Временная сложность O(logN), что намного луче, чем О(N).например, при массиве длинной 10^9 элементов, необходимо примерно 32 сравнения.
Изменить число в этой структуре еще проще — надо пройти по всем вершинам от заданной (n-1+k) до 1й, и если значение в текущей меньше чем новое, то заменить его. Это так же занимает O(log N) времени.

Range Minimum Query (RMQ)

Запрос минимума на отрезке

Вход: массив чисел, два числа (начало и конец отрезка в массиве)

Выход: минимальное значение на данном отрезке
Алгоритм:
Динамика (дерево отрезков)
1. Дополняем исходный массив до степени двойки бесконечно большими элементами.
2. Строим дерево отрезков (двоичное дерево: листья - значения элементов массива; вершины - минимум из дочерних листьев)
3. (Фундаментальный отрезок - такой отрезок, что существует вершина в дереве, которой он соответсвует) Заведем два указателя l и r, и установим указывающими на концы исходного отрезка (если l (r) указывает на правый (левый) дочерний элемент, то эта вершина принадлежит разбиению на фундоментальные отрезки) сдвигаем указатели на уровень вверх.повторяем до тех пор пока указатели не совпадут.
Находя очередной фундоментальные отрезок, сравниваем его значение с имеющимся минимум, при необходимости обновляем минимум.
Оценка: препроцессинг O(n); запрос O(logn).

Степень двойки (Sparse Table)
Sparse Table, или разреженная таблица

 

Sparse Table – это таблица ST[][] такая, что ST[k][i] есть минимум на полуинтервале [A[i], A[i+2^k]). Иными словами, она содержит минимумы на всех отрезках, длина которых есть степень двойки.

Насчитаем массив ST[k][i] следующим образом. Понятно, что ST[0] просто и есть наш массив A. Далее воспользуемся понятным свойством:

ST[k][i] = min(ST[k-1][i], ST[k-1][i + 2^k — 1]). Благодаря нему мы можем сначала посчитать ST[1], потом ST[2] и т. д.

Заметим, что в нашей таблице O(nlogn) элементов, потому что номера уровней должны быть не больше logn, т. к. при больших значениях k длина полуинтервала становится больше длины всего массива и хранить соответствующие значения бессмысленно. И на каждом уровне O(n) элементов.

А теперь главный вопрос: зачем мы всё это считали? Заметим, что любой отрезок массива разбивается на два перекрывающихся подотрезка длиною в степень двойки.

 

 

Получаем простую формулу для вычисления RMQ(i, j). Если k = log(j – i + 1), то RMQ(i, j) = min(ST(i, k), ST(j – 2k + 1, k)). Тем самым, получаем алгоритм за (O(nlogn), O(1)). Ура!

 

…почти получаем. Как мы логарифм считать собрались за O(1)? Проще всего его тоже предподсчитать для всех значений, не превосходящих n. Понятно, что асимптотика препроцессинга от этого не изменится.
Оценка: препроцессинг O(nlogn);
запрос O(1).