Амортизационная стоимость (анализ)
Амортизационный анализ — метод подсчета времени, требуемого для выполнения последовательности операций над структурой данных. При этом время усредняется по всем выполняемым операциям, и анализируется средняя производительность операций в худшем случае.
Такой анализ чаще всего используется, чтобы показать, что даже если некоторые из операций последовательности являются дорогостоящими, то при усреднении по всем операциям средняя их стоимость будет небольшой за счёт низкой частоты встречаемости. Это оценка среднего времени выполнения операций для худшего случая.
Средняя амортизационная стоимость операций — величина  , находящаяся по формуле:
, находящаяся по формуле: 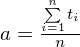 , где
, где 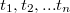 - время выполнения операций
- время выполнения операций 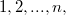 совершённых над структурой данных.
совершённых над структурой данных.
Амортизационный анализ использует следующие методы:
1. Метод усреднения (метод группового анализа).
2. Метод потенциалов.
3. Метод предоплаты (метод бухгалтерского учета).
Метод усреднения
В методе усреднения амортизационная стоимость операций определяется напрямую по формуле, указанной выше: суммарная стоимость всех операций алгоритма делится на их количество.
Пример
Рассмотрим стек с операцией 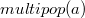 — извлечение из стека
— извлечение из стека  элементов. В худшем случае она работает за
элементов. В худшем случае она работает за 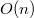 времени, если удаляются все элементы массива. Однако прежде чем удалить элемент, его нужно добавить в стек. Итак, если в стеке было не более
времени, если удаляются все элементы массива. Однако прежде чем удалить элемент, его нужно добавить в стек. Итак, если в стеке было не более 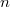 элементов, то в худшем случае с каждым из них могли быть произведены 2 операции - добавление в стек и извлечение из него. Например, если было
элементов, то в худшем случае с каждым из них могли быть произведены 2 операции - добавление в стек и извлечение из него. Например, если было 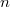 операций
операций  - добавление в стек, стоимость каждой
- добавление в стек, стоимость каждой  , и одна операция
, и одна операция 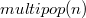 , то суммарное время всех операций —
, то суммарное время всех операций — 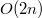 , всего операций
, всего операций 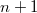 , а значит, амортизационная стоимость операции —
, а значит, амортизационная стоимость операции —  .
.
Метод предоплаты
Представим, что использование определенного количества времени равносильно использованию определенного количества монет (плата за выполнение каждой операции). В методе предоплаты каждому типу операций присваивается своя учётная стоимость. Эта стоимость может быть больше фактической, в таком случае лишние монеты используются как резерв для выполнения других операций в будущем, а может быть меньше, тогда гарантируется, что текущего накопленного резерва достаточно для выполнения операции.
Мы должны выбирать учетные стоимости так, чтобы сумма фактических стоимостей не превосходила суммы учетных стоимостей, то есть, чтобы резерв оставался неотрицательным в любой момент работы.
Пример
Опять же рассмотрим стек с операцией 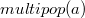 . При выполнении операции
. При выполнении операции  будем использовать две монеты — одну для самой операции, а вторую — в качестве резерва. Тогда для операций
будем использовать две монеты — одну для самой операции, а вторую — в качестве резерва. Тогда для операций 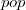 и
и 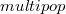 учётную стоимость можно принять равной нулю и использовать для удаления элемента монету, оставшуюся после операции
учётную стоимость можно принять равной нулю и использовать для удаления элемента монету, оставшуюся после операции  .
.
Таким образом, для каждой операции требуется  монет, а значит, cредняя амортизационная стоимость операций
монет, а значит, cредняя амортизационная стоимость операций 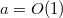 .
.
Метод потенциалов
Обобщение метода предоплаты. Самый точный
Введём для каждого состояния структуры данных величину 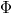 — потенциал (функция из множества состояний структуры в действительные числа). Изначально потенциал равен
— потенциал (функция из множества состояний структуры в действительные числа). Изначально потенциал равен 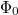 , а после выполнения
, а после выполнения  -ой операции —
-ой операции — 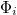 . Стоимость
. Стоимость  -ой операции обозначим
-ой операции обозначим 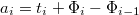 . Если удалось придумать такую Ф, что Ф(Dn)>= Ф(D0), то суммарная учетная стоимость даст верхнюю оценку для реальной стоимости nопераций.
. Если удалось придумать такую Ф, что Ф(Dn)>= Ф(D0), то суммарная учетная стоимость даст верхнюю оценку для реальной стоимости nопераций.
Сумма ai>= сумма ti
Пример
В качестве примера вновь рассмотрим стек с операцией 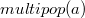 . Пусть потенциал — это количество элементов в стеке. Тогда:
. Пусть потенциал — это количество элементов в стеке. Тогда:
1.1) 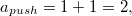 т. к. время выполнения операции
т. к. время выполнения операции  — 1, и изменение потенциала — тоже 1.
— 1, и изменение потенциала — тоже 1.
1.2) 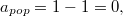 т. к. время выполнения операции
т. к. время выполнения операции 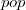 — 1, а изменение потенциала — -1.
— 1, а изменение потенциала — -1.
1.3) 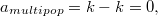 т. к. время выполнения операции
т. к. время выполнения операции  — k, а изменение потенциала — -k.
— k, а изменение потенциала — -k.
Коль скоро учетная стоимость каждой операции не превосходит 2, стоимость последовательности nопераций, начинающихся с пустого стека – есть O(n).
Фибоначчиева Куча
Фибоначчиево дерево — биномиальное дерево, где у каждой вершины удалено не более одного ребенка.
Порядок фибоначчиева дерева — порядок соответствующего биномиального дерева, из которого оно получено.
Степень вершины — количество дочерних узлов данной вершины.
Фибоначчиева куча — набор фибоначчиевых деревьев, корни которых объединены в неупорядоченный циклический двусвязный список. В отличие от биномиальной кучи, степени корней не обязаны быть попарно различными. Суть дерева в том, что любая операция, которая не требует удаления элемента из кучи, происходит за константу. Удаление же происходит примерно за O (log(n)) 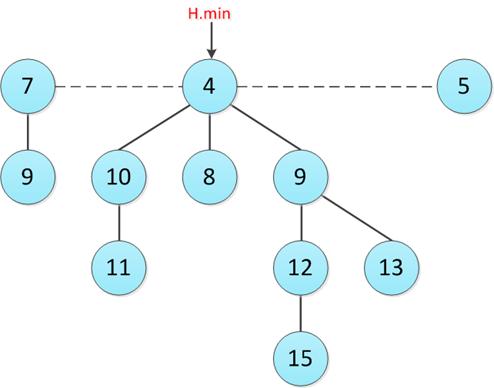
Пример Фибоначчиево дерева.
Структура
· Каждый узел  в куче
в куче 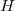 содержит следующие указатели и поля:
содержит следующие указатели и поля:  — поле, в котором хранится ключ;
— поле, в котором хранится ключ; 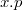 — указатель на родительский узел;
— указатель на родительский узел; 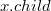 — указатель на один из дочерних узлов (левый);
— указатель на один из дочерних узлов (левый); 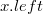 — указатель на левый сестринский узел;
— указатель на левый сестринский узел; 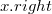 — указатель на правый сестринский узел;
— указатель на правый сестринский узел; 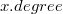 — поле, в котором хранится количество дочерних узлов;
— поле, в котором хранится количество дочерних узлов; 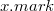 — логическое значение, которое показывает, удаляли ли мы дочерние узлы данной вершины.
— логическое значение, которое показывает, удаляли ли мы дочерние узлы данной вершины.
· Дочерние узлы  объединены при помощи указателей
объединены при помощи указателей 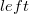 и
и 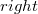 в циклический двусвязный список.
в циклический двусвязный список.
· Корни всех деревьев в 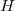 связаны при помощи указателей
связаны при помощи указателей 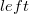 и
и 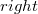 в циклический двусвязный список корней.
в циклический двусвязный список корней.
· Порядок узлов – любой (в циклическом списке)
· Обращение к 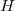 выполняется посредством указателя
выполняется посредством указателя 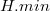 на корень дерева с минимальным ключом. Этот узел называется минимальным узлом
на корень дерева с минимальным ключом. Этот узел называется минимальным узлом 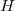 .
.
· Текущее количество узлов в 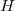 хранится в
хранится в 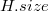 .
.
· Максимальная степень 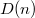 произвольной вершины в фибоначчиевой куче с
произвольной вершины в фибоначчиевой куче с 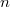 вершинами равна
вершинами равна 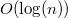
Циклический двусвязный список обладает двумя преимуществами для использования в фибоначчиевых кучах. Во-первых, удаление элемента из такого списка выполняется за время  . Во-вторых, если имеется два таких списка, их легко объединить в один за время
. Во-вторых, если имеется два таких списка, их легко объединить в один за время 
Вводим потенциал:
Ф(Н) = t(H) + 2m(H), где t(H) – число деревьев в корневом списке кучи, а m(H) – количество отмеченных вершин (mark ==true)
Ф(H) >= 0 è удовлетворяет условию использования потенциала. Если H – пустая куча, то == 0
Основные операции:
| операция
| Ci - реальная стоимость
| Фi – Ф(i-1)
|
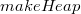
| 
|
|
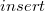
| 
|
|
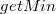
| 
|
|
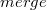
| 
|
|
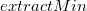
| 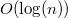
| D(n)+1+2m(H)
|
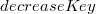
| 
|
|
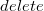
| 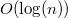
|
|
MakeHeap
Создается новый пустой корневой список, в 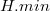 устанавливается значение
устанавливается значение 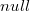 . Реальное время работы —
. Реальное время работы —  .
.
insert
Вставка элемента в фибоначчиеву кучу также тривиальна: создается новая куча из одного элемента и сливается с текущей. Реальное время работы составляет  .
.
GetMin
Возвращает указатель 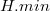 . Реальное время работы —
. Реальное время работы —  .
.
Merge
Слияние двух фибоначчиевых куч происходит просто: объединяем списки этих куч в один, релаксируем минимум. Реальное время работы —  .
.
Ф(H) – (Ф(Н1) + Ф(Н2)) = t(H) – t(H1) – t(H2) + 2(m(H) – m(H1) – m(H2)) = 0
ExtractMin
Первая рассматриваемая операция, в ходе которой меняется структура кучи. Здесь используется вспомогательная процедура 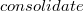 . Возьмем указатель на
. Возьмем указатель на 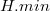 , удалим эту вершину. Ее поддеревья (их не более, чем
, удалим эту вершину. Ее поддеревья (их не более, чем 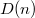 , где
, где 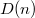 — максимальная степень вершины в куче) объединим с корневым списком. Теперь вызываем процедуру
— максимальная степень вершины в куче) объединим с корневым списком. Теперь вызываем процедуру 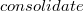 . После этой операции в списке корней остается не более чем
. После этой операции в списке корней остается не более чем 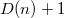 узлов, среди которых нужно найти минимальный.
узлов, среди которых нужно найти минимальный.
z = min(H)
if (z!= null)
then
for каждый ребенок x вершины z
do добавить x в корневой список H
p[x] = null
удалить z из корневого списка H
if (z == right[z])
then min(H) = null
else
min(H) = right[z]
Consolidate(H)
Returnz;
Consolidate
Данная процедура принимает кучу и преобразует ее таким образом, что в корневом списке остается не более 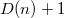 вершин.
вершин.
Для этого возьмем массив списков указателей на корни деревьев 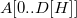 , где
, где 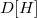 — максимальная степень вершины в текущем корневом списке.
— максимальная степень вершины в текущем корневом списке.
Затем происходит процесс, аналогичный слиянию биномиальных куч: добавляем поочередно каждый корень, смотря на его степень. Пусть она равна 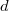 . Если в соответствующей ячейке
. Если в соответствующей ячейке  еще нету вершины, записываем текущую вершину туда. Иначе подвешиваем одно дерево к другому, и пытаемся также добавить дерево, степень корня которого уже равна
еще нету вершины, записываем текущую вершину туда. Иначе подвешиваем одно дерево к другому, и пытаемся также добавить дерево, степень корня которого уже равна 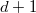 . Продолжаем, пока не найдем свободную ячейку.Когда подсоединяем x к y, убираем пометку с x
. Продолжаем, пока не найдем свободную ячейку.Когда подсоединяем x к y, убираем пометку с x
Учетная стоимость 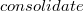 равна
равна 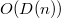 .
.
Иначе говоря:
Еслиx->degree =d
Если A[d] == null, то A[d] = x
Иначе, если A[d] == y, то z = Link(x,y) – y станет сыном x, A[d] == null, аналогично далее. Когда подсоединяем x к y, убираем пометку с x
Учетная стоимость 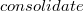 равна
равна 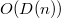 . Докажем это вместе с ExtractMin:
. Докажем это вместе с ExtractMin:
Нужно O(D(n)) действий, чтобы поместить детей удаляемой вершины в корень. Затем начальный и конечный этапы consolidate (создать массив Aи, находя минимум, поместить деревья в корень) тоже за O(D(n)). Остальная часть consolidate – за O(D(n)) + O(число вызовов Link). Но при каждом вызове Link – длина корневого списка уменьшается на 1, а число отмеченных вершин может только уменьшиться. Так что умножим потенциал на подходящую константу общая сложность – O(D(n))
DecreaseKey
Основная идея: хотим, чтобы учетная стоимость данной операции была 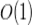 . Было бы хорошо, чтобы вершина не всплывала до корня, и тогда дерево не придется сильно перестраивать. Для этого при удобном случае будем вырезать поддерево полностью и перемещать его в корневой список. Итак, сам алгоритм:
. Было бы хорошо, чтобы вершина не всплывала до корня, и тогда дерево не придется сильно перестраивать. Для этого при удобном случае будем вырезать поддерево полностью и перемещать его в корневой список. Итак, сам алгоритм:
1. Проверяем, если новое значение ключа все же не меньше значения ключа родителя, то все хорошо, и мы выходим.
2. Иначе, вырезаем дерево с текущей вершиной в корневой список, и производим каскадное вырезание родителя.
If (k > key[x])
Error
Key[x] = k
y = p[x]
if (y!= null && key[x] < key[y])
cut(H,x,y)
CascadingCut(H,y)
If (key[x] <key[min(H)])
Min(H) = x
Cut
При вырезании вершины мы удаляем ее из списка детей своего родителя, уменьшаем степень ее родителя (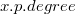 ), добавляем вершину в корневой список H и снимаем пометку с текущей вершины (
), добавляем вершину в корневой список H и снимаем пометку с текущей вершины (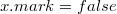 ).
).
CascadingCut
Перед вызовом каскадного вырезания нам известно, удаляли ли ребенка у этой вершины. Если у вершины до этого не удаляли дочерний узел (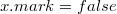 ), то мы помечаем эту вершину (
), то мы помечаем эту вершину (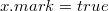 ) и прекращаем выполнение операции. В противном случае применяем операцию
) и прекращаем выполнение операции. В противном случае применяем операцию 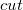 для текущей вершины и запускаем каскадное вырезание от родителя – для поддержки инварианта из определения фибоначчиева дерева
для текущей вершины и запускаем каскадное вырезание от родителя – для поддержки инварианта из определения фибоначчиева дерева
z = p[y]
if (z!= null)
if (mark[y] == false)
mark[y] = true
else
cut(H,y,z)
CascadingCut(H,z)
Время работы
Докажем, что амортизированное время работы операции 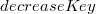 есть
есть  . Поскольку в процедуре нет циклов, ее время работы определяется лишь количеством рекурсивных вызовов каскадного вырезания.
. Поскольку в процедуре нет циклов, ее время работы определяется лишь количеством рекурсивных вызовов каскадного вырезания.
Пусть мы вызвали процедуру каскадного вырезания 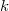 раз. Так как реальное время работы операции
раз. Так как реальное время работы операции 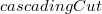 без учета рекурсии составляет
без учета рекурсии составляет  , то реальное время работы операции
, то реальное время работы операции 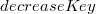 —
— 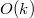 .
.
Рассмотрим, как изменится потенциал в результате выполнения данной операции. Пусть 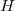 — фибоначчиева куча до вызова
— фибоначчиева куча до вызова 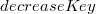 . Тогда после
. Тогда после 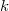 рекурсивных вызовов операции
рекурсивных вызовов операции 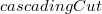 вершин с пометкой
вершин с пометкой 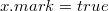 стало как минимум на
стало как минимум на 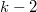 меньше, потому что каждый вызов каскадного вырезания, за исключением последнего, уменьшает количество помеченных вершин на одну, и в результате последнего вызова одну вершину мы можем пометить. В корневом списке прибавилось
меньше, потому что каждый вызов каскадного вырезания, за исключением последнего, уменьшает количество помеченных вершин на одну, и в результате последнего вызова одну вершину мы можем пометить. В корневом списке прибавилось 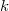 новых деревьев (
новых деревьев (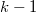 дерево за счет каскадного вырезания и еще одно из-за самого первого вызова операции
дерево за счет каскадного вырезания и еще одно из-за самого первого вызова операции 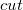 ).
).
В итоге, изменение потенциала составляет: 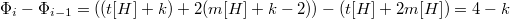 . Следовательно, амортизированная стоимость не превышает
. Следовательно, амортизированная стоимость не превышает 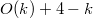 . Но поскольку мы можем соответствующим образом масштабировать единицы потенциала, то амортизированная стоимость операции
. Но поскольку мы можем соответствующим образом масштабировать единицы потенциала, то амортизированная стоимость операции 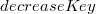 равна
равна  .
.
Delete
Удаление вершины реализуется через уменьшение ее ключа до 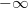 и последующим извлечением минимума. Амортизированное время работы:
и последующим извлечением минимума. Амортизированное время работы: 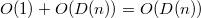 .
.
Поскольку ранее мы показали, что 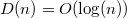 , то соответствующие оценки доказаны.
, то соответствующие оценки доказаны.
| Лемма:
|
Для всех целых 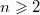
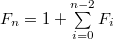 , где , где 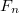 — — 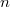 -ое число Фибоначчи, определяемое формулой: -ое число Фибоначчи, определяемое формулой:
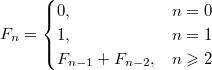
|
| Доказательство:
|
Докажем лемму по индукции:
при 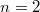
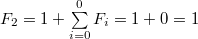 , что действительно верно.
По индукции предполагаем, что , что действительно верно.
По индукции предполагаем, что 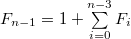 . Тогда . Тогда
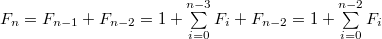 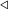
|
| Лемма:
|
Фибоначчиево дерево порядка 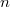 содержит не менее содержит не менее 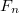 вершин. вершин.
|
| Доказательство:
|
Докажем это утверждение по индукции. Пусть 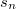 — минимальный размер фибоначчиева дерева порядка n.
При — минимальный размер фибоначчиева дерева порядка n.
При 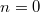
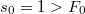 .
При .
При 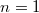
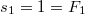 . (Можем удалить 1 ребенка)
Предположим по индукции, что для всех . (Можем удалить 1 ребенка)
Предположим по индукции, что для всех 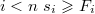 . Пусть в нашем дереве удалено поддерево порядка . Пусть в нашем дереве удалено поддерево порядка 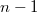 (худший). Тогда (худший). Тогда
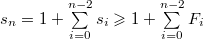 Но по предыдущей лемме
Но по предыдущей лемме 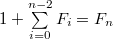 . Следовательно, . Следовательно, 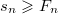 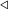
|
| Лемма:
|
Максимальная степень 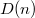 произвольной вершины в фибоначчиевой куче с произвольной вершины в фибоначчиевой куче с 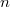 вершинами равна вершинами равна 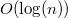
|
| Доказательство:
|
Пусть  — произвольная вершина в фибоначчиевой куче с — произвольная вершина в фибоначчиевой куче с 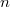 вершинами, и пусть вершинами, и пусть 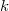 — степень вершины — степень вершины  . Тогда по доказанному выше в дереве, корень которого . Тогда по доказанному выше в дереве, корень которого  , содержится не менее , содержится не менее 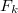 вершин, что в свою очередь по лемме равно вершин, что в свою очередь по лемме равно 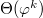 - доказывалось на лекции как очевидное - доказывалось на лекции как очевидное 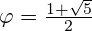 . То есть . То есть
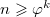 (выполнено для поддерева ведь, значит это верно)
Логарифмируя по основанию (выполнено для поддерева ведь, значит это верно)
Логарифмируя по основанию 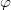 , получаем , получаем
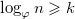 Таким образом, максимальная степень
Таким образом, максимальная степень 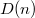 произвольной вершины равна произвольной вершины равна 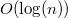 . . 
|



 , находящаяся по формуле:
, находящаяся по формуле: 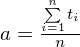 , где
, где 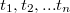 - время выполнения операций
- время выполнения операций 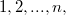 совершённых над структурой данных.
совершённых над структурой данных.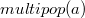 — извлечение из стека
— извлечение из стека 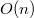 времени, если удаляются все элементы массива. Однако прежде чем удалить элемент, его нужно добавить в стек. Итак, если в стеке было не более
времени, если удаляются все элементы массива. Однако прежде чем удалить элемент, его нужно добавить в стек. Итак, если в стеке было не более 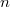 элементов, то в худшем случае с каждым из них могли быть произведены 2 операции - добавление в стек и извлечение из него. Например, если было
элементов, то в худшем случае с каждым из них могли быть произведены 2 операции - добавление в стек и извлечение из него. Например, если было  - добавление в стек, стоимость каждой
- добавление в стек, стоимость каждой  , и одна операция
, и одна операция 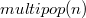 , то суммарное время всех операций —
, то суммарное время всех операций — 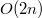 , всего операций
, всего операций 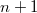 , а значит, амортизационная стоимость операции —
, а значит, амортизационная стоимость операции — 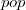 и
и 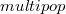 учётную стоимость можно принять равной нулю и использовать для удаления элемента монету, оставшуюся после операции
учётную стоимость можно принять равной нулю и использовать для удаления элемента монету, оставшуюся после операции 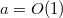 .
.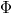 — потенциал (функция из множества состояний структуры в действительные числа). Изначально потенциал равен
— потенциал (функция из множества состояний структуры в действительные числа). Изначально потенциал равен 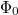 , а после выполнения
, а после выполнения  -ой операции —
-ой операции — 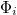 . Стоимость
. Стоимость 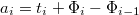 . Если удалось придумать такую Ф, что Ф(Dn)>= Ф(D0), то суммарная учетная стоимость даст верхнюю оценку для реальной стоимости nопераций.
. Если удалось придумать такую Ф, что Ф(Dn)>= Ф(D0), то суммарная учетная стоимость даст верхнюю оценку для реальной стоимости nопераций.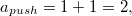 т. к. время выполнения операции
т. к. время выполнения операции 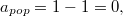 т. к. время выполнения операции
т. к. время выполнения операции 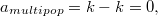 т. к. время выполнения операции
т. к. время выполнения операции  — k, а изменение потенциала — -k.
— k, а изменение потенциала — -k.
 в куче
в куче 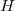 содержит следующие указатели и поля:
содержит следующие указатели и поля:  — поле, в котором хранится ключ;
— поле, в котором хранится ключ; 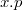 — указатель на родительский узел;
— указатель на родительский узел; 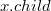 — указатель на один из дочерних узлов (левый);
— указатель на один из дочерних узлов (левый); 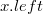 — указатель на левый сестринский узел;
— указатель на левый сестринский узел; 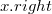 — указатель на правый сестринский узел;
— указатель на правый сестринский узел; 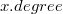 — поле, в котором хранится количество дочерних узлов;
— поле, в котором хранится количество дочерних узлов; 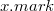 — логическое значение, которое показывает, удаляли ли мы дочерние узлы данной вершины.
— логическое значение, которое показывает, удаляли ли мы дочерние узлы данной вершины.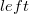 и
и 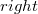 в циклический двусвязный список.
в циклический двусвязный список.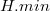 на корень дерева с минимальным ключом. Этот узел называется минимальным узлом
на корень дерева с минимальным ключом. Этот узел называется минимальным узлом 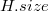 .
.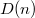 произвольной вершины в фибоначчиевой куче с
произвольной вершины в фибоначчиевой куче с 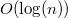
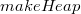
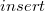
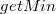
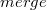
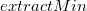
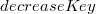
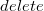
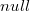 . Реальное время работы —
. Реальное время работы — 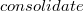 . Возьмем указатель на
. Возьмем указатель на 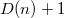 узлов, среди которых нужно найти минимальный.
узлов, среди которых нужно найти минимальный.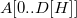 , где
, где 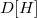 — максимальная степень вершины в текущем корневом списке.
— максимальная степень вершины в текущем корневом списке.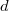 . Если в соответствующей ячейке
. Если в соответствующей ячейке  еще нету вершины, записываем текущую вершину туда. Иначе подвешиваем одно дерево к другому, и пытаемся также добавить дерево, степень корня которого уже равна
еще нету вершины, записываем текущую вершину туда. Иначе подвешиваем одно дерево к другому, и пытаемся также добавить дерево, степень корня которого уже равна 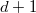 . Продолжаем, пока не найдем свободную ячейку.Когда подсоединяем x к y, убираем пометку с x
. Продолжаем, пока не найдем свободную ячейку.Когда подсоединяем x к y, убираем пометку с x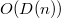 .
.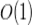 . Было бы хорошо, чтобы вершина не всплывала до корня, и тогда дерево не придется сильно перестраивать. Для этого при удобном случае будем вырезать поддерево полностью и перемещать его в корневой список. Итак, сам алгоритм:
. Было бы хорошо, чтобы вершина не всплывала до корня, и тогда дерево не придется сильно перестраивать. Для этого при удобном случае будем вырезать поддерево полностью и перемещать его в корневой список. Итак, сам алгоритм: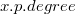 ), добавляем вершину в корневой список H и снимаем пометку с текущей вершины (
), добавляем вершину в корневой список H и снимаем пометку с текущей вершины (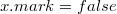 ).
).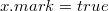 ) и прекращаем выполнение операции. В противном случае применяем операцию
) и прекращаем выполнение операции. В противном случае применяем операцию 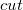 для текущей вершины и запускаем каскадное вырезание от родителя – для поддержки инварианта из определения фибоначчиева дерева
для текущей вершины и запускаем каскадное вырезание от родителя – для поддержки инварианта из определения фибоначчиева дерева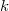 раз. Так как реальное время работы операции
раз. Так как реальное время работы операции 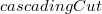 без учета рекурсии составляет
без учета рекурсии составляет 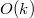 .
.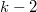 меньше, потому что каждый вызов каскадного вырезания, за исключением последнего, уменьшает количество помеченных вершин на одну, и в результате последнего вызова одну вершину мы можем пометить. В корневом списке прибавилось
меньше, потому что каждый вызов каскадного вырезания, за исключением последнего, уменьшает количество помеченных вершин на одну, и в результате последнего вызова одну вершину мы можем пометить. В корневом списке прибавилось 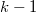 дерево за счет каскадного вырезания и еще одно из-за самого первого вызова операции
дерево за счет каскадного вырезания и еще одно из-за самого первого вызова операции 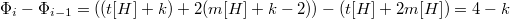 . Следовательно, амортизированная стоимость не превышает
. Следовательно, амортизированная стоимость не превышает 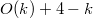 . Но поскольку мы можем соответствующим образом масштабировать единицы потенциала, то амортизированная стоимость операции
. Но поскольку мы можем соответствующим образом масштабировать единицы потенциала, то амортизированная стоимость операции 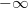 и последующим извлечением минимума. Амортизированное время работы:
и последующим извлечением минимума. Амортизированное время работы: 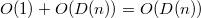 .
.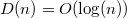 , то соответствующие оценки доказаны.
, то соответствующие оценки доказаны.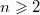
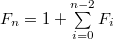 , где
, где 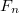 —
— 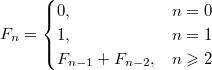
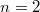
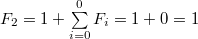 , что действительно верно.
По индукции предполагаем, что
, что действительно верно.
По индукции предполагаем, что 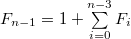 . Тогда
. Тогда
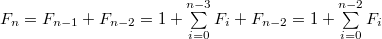
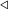
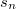 — минимальный размер фибоначчиева дерева порядка n.
При
— минимальный размер фибоначчиева дерева порядка n.
При 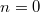
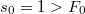 .
При
.
При 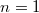
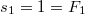 . (Можем удалить 1 ребенка)
Предположим по индукции, что для всех
. (Можем удалить 1 ребенка)
Предположим по индукции, что для всех 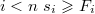 . Пусть в нашем дереве удалено поддерево порядка
. Пусть в нашем дереве удалено поддерево порядка 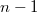 (худший). Тогда
(худший). Тогда
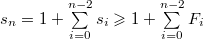 Но по предыдущей лемме
Но по предыдущей лемме 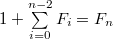 . Следовательно,
. Следовательно, 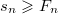
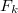 вершин, что в свою очередь по лемме равно
вершин, что в свою очередь по лемме равно 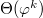 - доказывалось на лекции как очевидное
- доказывалось на лекции как очевидное 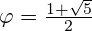 . То есть
. То есть
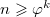 (выполнено для поддерева ведь, значит это верно)
Логарифмируя по основанию
(выполнено для поддерева ведь, значит это верно)
Логарифмируя по основанию 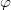 , получаем
, получаем
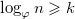 Таким образом, максимальная степень
Таким образом, максимальная степень 

