Производная и ее приложения
Ростов-на-Дону
1997 г.
Производная и ее приложения.
Формулы дифференцирования.
Справочный материал.
Пусть функция y=f(x) определена на промежутке Х. Если аргумент изменяется от фиксированного значения х до нового значения 
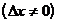 , то значение функции изменяется от
, то значение функции изменяется от 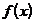 до
до 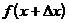 .
.
Дифференциальным отношением называется отношение приращения функции к приращению аргумента
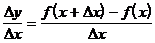
Это отношение измеряет среднюю скорость изменения функции y=f(x).
Производной функции y=f(x) в некоторой точке x называется предел отношения приращения функции к приращению аргумента при 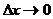 (если этот предел существует)
(если этот предел существует)
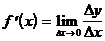 ,
,
а сам процесс нахождения производной - дифференцированием.
Производную обозначают символами

Таблица производных элементарных функций.
1. 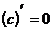
2. 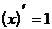
3. 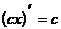
4. 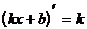
5. 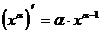
6. 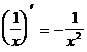
7. 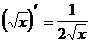
8. 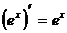
9. 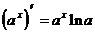
10. 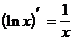
11. 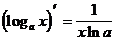
12. 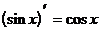
13. 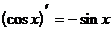
14. 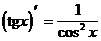
15. 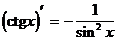
16. 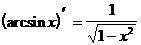
17. 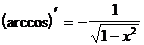
18. 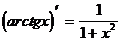
19. 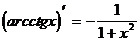
Пример 1. Вычислить производные:
1) 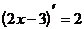 (формула 4)
(формула 4)
2) 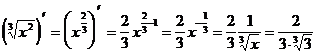 (формула 5)
(формула 5)
3) 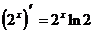 (формула 9)
(формула 9)
4) 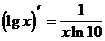 (формула 11)
(формула 11)
Производная суммы.
Производная суммы двух дифференцируемых в точке x функций u(x) и v(x) существует в этой точке и вычисляется по формуле:
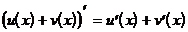
или короче
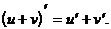 (1)
(1)
Пример 2. Вычислить производные:
1. 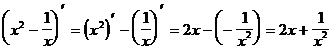
2. 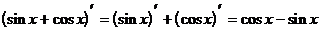
3. 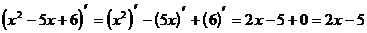
4. 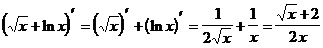
5. 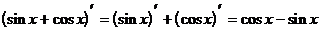
Производная произведения.
Производная произведения двух дифференцируемых в точке x функций u(x) и v(x) существует в этой точке и вычисляется по формуле:
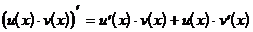
или короче
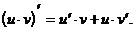 (2)
(2)
Если функция u=u(x) дифференцируема в точке х, а С – постоянная, то функция Cu дифференцируема в этой точке и
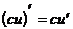 (3)
(3)
или короче: постоянный множитель можно выносить за знак производной.
Пример 3. Найти 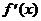 :
: 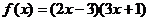 .
.
Решение. 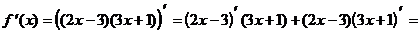
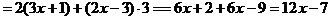 .
.
Была использована формула 4: 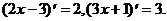
Производная частного.
Производная частного двух дифференцируемых в точке x функций u(x) и v(x) при условии, что функция v(x) не равна нулю в этой точке, существует в этой точке и вычисляется по формуле:
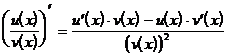
или короче
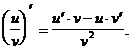 (4)
(4)
Пример 4. Найти значение производной функции 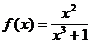 в точке х = 1:
в точке х = 1:
Решение.
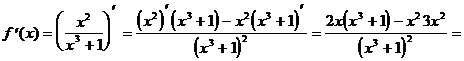

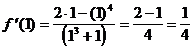
Ответ: 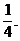
Понятие сложной функции.
Пример 5. Пусть требуется вычислить значение функции  в некоторой фиксированной точке x. Для этого нужно:
в некоторой фиксированной точке x. Для этого нужно:
1) вычислить 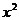 ;
;
2) найти значение синуса при полученном значении 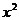 .
.
Иными словами, сначала надо найти значение функции 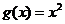 , а затем
, а затем 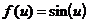 , аргумент u (u =g(x))в этом случае называют промежуточным, а x – независимой переменной.
, аргумент u (u =g(x))в этом случае называют промежуточным, а x – независимой переменной.
Пусть функция u=g(x) определена на некотором множестве X, а функция y=f(u) – на множестве значений функции u=g(x), тогда на множестве X определена функция y=f(g(x)), называемая сложной функцией.
Пример 6. Рассмотрим функцию 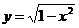 . Чтобы найти значение этой функции в фиксированной точке х, нужно сначала найти значение функции g(x) = 1 - x2, а потом найти значение
. Чтобы найти значение этой функции в фиксированной точке х, нужно сначала найти значение функции g(x) = 1 - x2, а потом найти значение 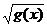 . В этом примере
. В этом примере 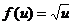 , где u = 1 - x 2.
, где u = 1 - x 2.
Пример 7. Составить сложную функцию 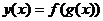 , если
, если 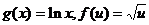 .
.
Решение. 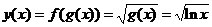 .
.
Задачи раздела I.
1. Найти производную функции в точке x0:
1) 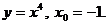
2) 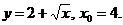
3) 
4) 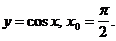
5) 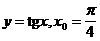
6) 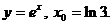
7) 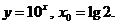
8) 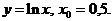
9) 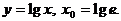
2. Найти производную функции, предварительно приведя ее к виду kxm(mÎZ).
1) 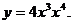 3)
3) 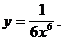
2) 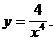 4)
4) 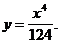
3. Приведя функцию к к виду kxa(aÎQ) найти ее производную.
1) 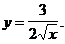
2) 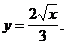
3) 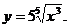
4) 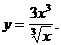
5) 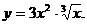
4. Используя формулу производной от суммы найти производную функции:
1) 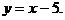
2) 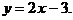
3) 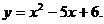
4) 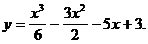
5) 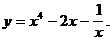
6) 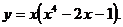
7) 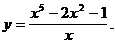
5. Используя формулы производной произведения или частного, найти производную функции:
1) 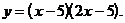
2) 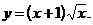
3) 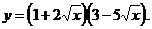
4) 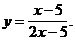
5) 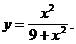
6) 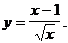
6. Используя правило дифференцирования сложной функции, найти производную функции:
1) 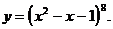
2) 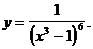
3) 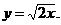
4) 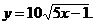
5) 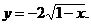
6) 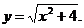
7) 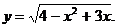
Задачи раздела II.
1. Найти производную функции в точке x0:
1) 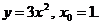
2) 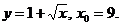
3) 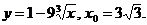
4) 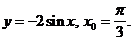
5) 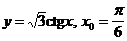
6) 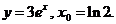
7) 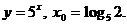
8) 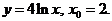
9) 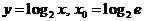
2. Найти производную функции, предварительно приведя ее к виду kxm(mÎZ).
1) 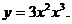
2) 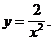
3) 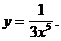
4) 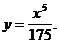
3. Приведя функцию к к виду kxa(aÎQ) найти ее производную.
1) 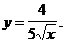
2) 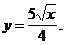
3) 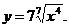
4) 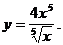
5) 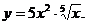
4. Используя формулу производной от суммы найти производную функции:
1) 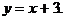
2) 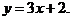
3) 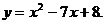
4) 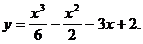
5) 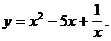
6) 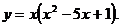
7) 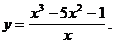
5. Используя формулы производной произведения или частного, найти производную функции:
1) 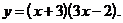
2) 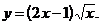
3) 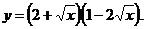
4) 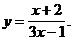
5) 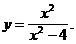
6) 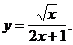
6. Используя правило дифференцирования сложной функции, найти производную функции:
1) 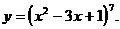
2) 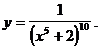
3) 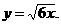
4) 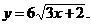
5) 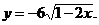
6) 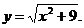
7) 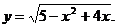
Решение задач раздела I.
1.
1) 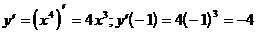
2) 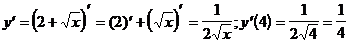
3) 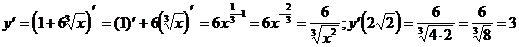
4) 
5) 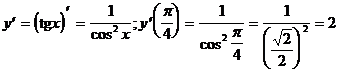
6) 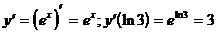
7) 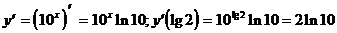
8) 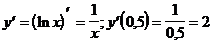
9) 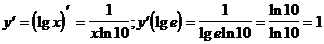
2.
10) 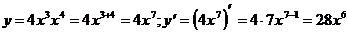
11) 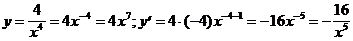
12) 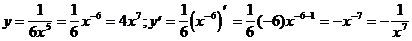
13) 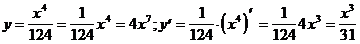
3.
1) 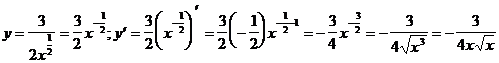
2) 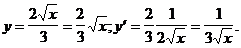
3) 
4) 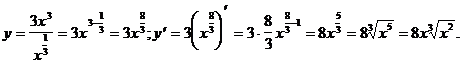
5) 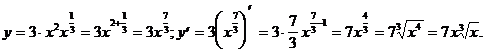
4.
1) 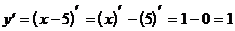
2) 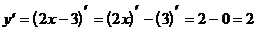
3) 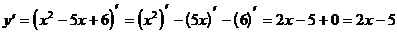
4) 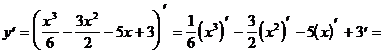
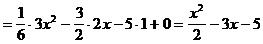
5) 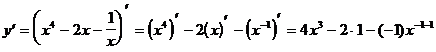
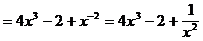
6) 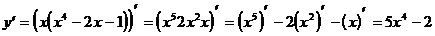
7) 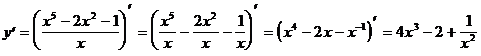
5.
1) 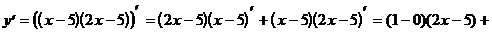
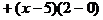
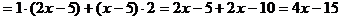
2) 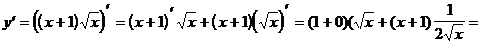
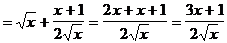
3) 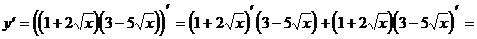
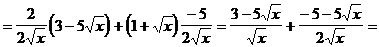
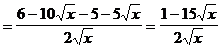
4) 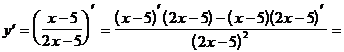
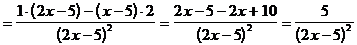
5) 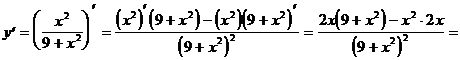
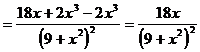
6) 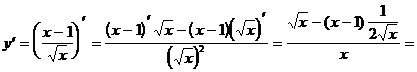
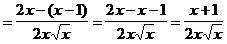
6.
1) 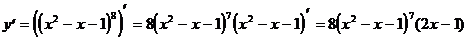
2) 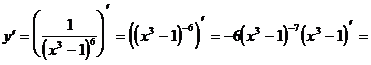

3) 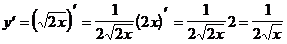
4) 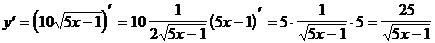
5) 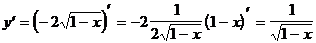
6) 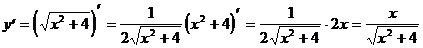
7) 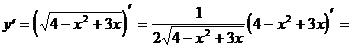
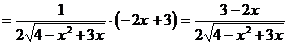
Ответы к задачам раздела II.
1.
1) 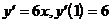 ;
;
2) 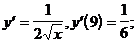
3) 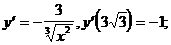
4) 
5) 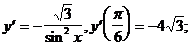
6) 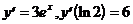 ;
;
7) 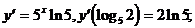
8) 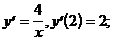
9) 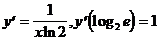 .
.
2.
1) 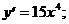 2)
2) 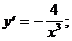 3)
3) 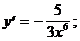 4)
4) 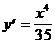 .
.
3.
1) 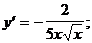 2)
2) 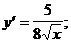 3)
3) 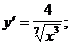 4)
4) 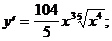 5)
5) 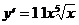 .
.
4.
1) 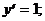
2) 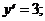
3) 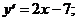
4) 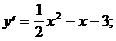
5) 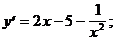
6) 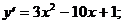
7) 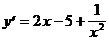 .
.
5.
1) 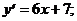
1) 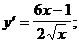
2) 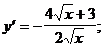
3) 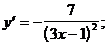
4) 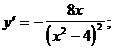
5) 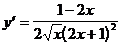 .
.
6.
1) 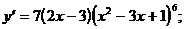
2) 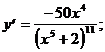
3) 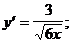
4) 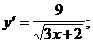
5) 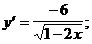
6) 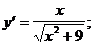
7) 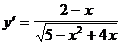 .
.
Справочной материал.
1. Те точки из области определения функции (О.О.Ф.), в которых 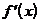 обращается в нуль или не существует, называются критическими точками этой функции.
обращается в нуль или не существует, называются критическими точками этой функции.
Исследование функции на монотонность основано на следующих двух утверждениях.
2. Необходимое условие монотонности. Если функция 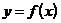 дифференцируема на промежутке (a;b) и возрастает (убывает) на нем, то ее производная
дифференцируема на промежутке (a;b) и возрастает (убывает) на нем, то ее производная 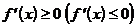 во всех точках этого промежутка.
во всех точках этого промежутка.
3. Достаточное условие монотонности. Если функция 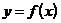 дифференцируема на промежутке (a;b) и во всех точках этого промежутка ее производная
дифференцируема на промежутке (a;b) и во всех точках этого промежутка ее производная 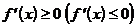 , то функция возрастает (убывает) на этом промежутке.
, то функция возрастает (убывает) на этом промежутке.
Справочный материал.
1. Точка x=x0 из области определения функции f(x) называется точкой минимума (максимума) этой функции, если у этой точки существует окрестность такая, что для всех x¹x0 из этой окрестности выполняется неравенство 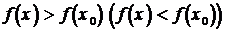 .
.
2. Точки максимума 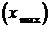 и минимума
и минимума 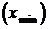 функции объединяются общим термином – точки экстремума.
функции объединяются общим термином – точки экстремума.
3. Значения функции в точке экстремума называются соответственно максимумом 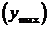 и минимумом
и минимумом 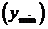 функции (или экстремумами самой функции).
функции (или экстремумами самой функции).
4. Функция y = f(x), график которой расположен на рис.1, в точках x1 и x3 имеет минимумы 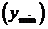 , а в точках x2 и x4 – максимумы
, а в точках x2 и x4 – максимумы 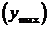 . Точки a и b не считаются точками экстремума функции f(x), т.к. у этих точек нет окрестности, целиком входящей в область определения функции.
. Точки a и b не считаются точками экстремума функции f(x), т.к. у этих точек нет окрестности, целиком входящей в область определения функции.
5. Исследование функции на экстремум основано на следующих двух утверждениях:
а). Необходимое условие экстремума. Если точка x0 является точкой экстремума функции y = f(x), то производная в этой точке равна нулю: 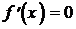 .
.
б). Достаточные условие экстремума.
Если в окрестности точки x0 производная меняет знак с плюса на минус, то x0 есть точка максимума.
Если в окрестности точки x0 производная меняет знак с минуса на плюс, то x0 есть точка минимума.
Справочный материал.
1. Наибольшим (наименьшим) значением функции y= f(x) на промежутке X называется такое число M(m), что существует такая точка x0, принадлежащая этому промежутку, что 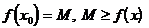
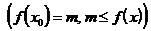 для всех x из этого промежутка.
для всех x из этого промежутка.
2. Наибольшее и наименьшее значения функции на промежутке X дифференцируемая функция f(x) может принимать либо на концах промежутка (если это числа), либо в критических точках, лежащих внутри промежутка.
3. На рис.1 функция y = f(x) достигает наибольшее значение на отрезке [ a;b ] в точке x=a и наименьшее значение в точке x=b:
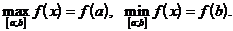
На интервале (a;b) в этом случае функция не достигает ни наименьшего ни наибольшего значений.
4. Если дифференцируемая функция f(x) на промежутке X имеет единственную точку экстремума и в этот экстремум – максимум (минимум), то в этой точке достигается наибольшее (наименьшее) значение функции.
5. На рис.1 функция y=f(x) на отрезке [x1;x3] в точке x=x2 имеет единственный максимум:
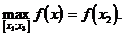
Функция y=f(x) на отрезке [x2;x4] в точке x=x3 имеет единственный минимум:
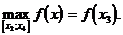
Задачи раздела I.
1. Найти производную функции в точке x0:
1) 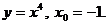
2) 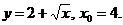
3) 
4) 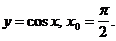
5) 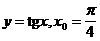
6) 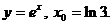
7) 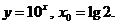
8) 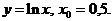
9) 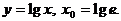
2. Найти производную функции, предварительно приведя ее к виду kxm(mÎZ).
1) 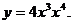 3)
3) 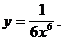
2) 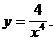 4)
4) 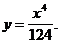
3. Приведя функцию к к виду kxa(aÎQ) найти ее производную.
1) 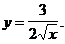
2) 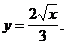
3) 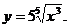
4) 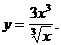
5) 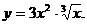
4. Используя формулу производной от суммы найти производную функции:
1) 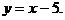
2) 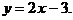
3) 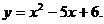
4) 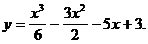
5) 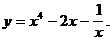
6) 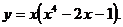
7) 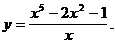
5. Используя формулы производной произведения или частного, найти производную функции:
1) 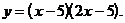
2) 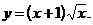
3) 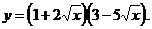
4) 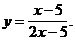
5) 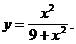
6) 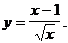
6. Используя правило дифференцирования сложной функции, найти производную функции:
1) 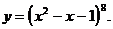
2) 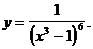
3) 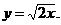
4) 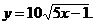
5) 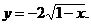
6) 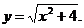
7) 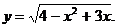
7. Найти критические точки функции:
1) 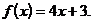
2) 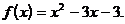
3) 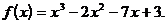
4) 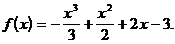
5) 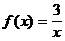
6) 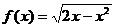
8. Найти промежутки возрастания и убывания функции:
1) 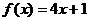
2) 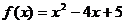
3) 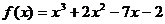
4) 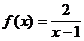
5) 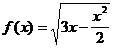
9. Найти точки экстремума и экстремумы функции.
1) 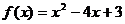
2) 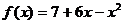
3) 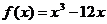
4) 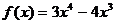
5) 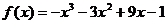
6) 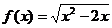
10. Найти наибольшее и наименьшее значения функции на промежутке.
1) 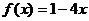 на [-3; 2]
на [-3; 2]
2) 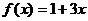 на [-2; 3)
на [-2; 3)
3) 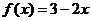 на (-1; 2]
на (-1; 2]
4) 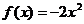 на [-2; 1]
на [-2; 1]
5) 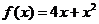 на [-1; 0]
на [-1; 0]
6) 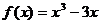 на [0; 3]
на [0; 3]
11. Периметр прямоугольника равен 40. Найти его стороны, при которых его площадь будет наибольшей.
Задачи раздела II.
1. Найти производную функции в точке x0:
1) 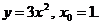
2) 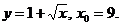
3) 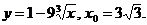
4) 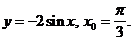
5) 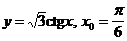
6) 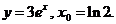
7) 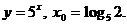
8) 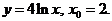
9) 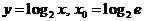
2. Найти производную функции, предварительно приведя ее к виду kxm(mÎZ).
1) 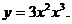
2) 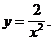
3) 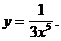
4) 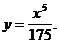
3. Приведя функцию к к виду kxa(aÎQ) найти ее производную.
1) 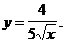
2) 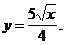
3) 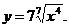
4) 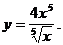
5) 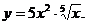
4. Используя формулу производной от суммы найти производную функции:
1) 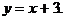
2) 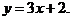
3) 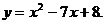
4) 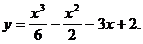
5) 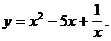
6) 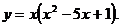
7) 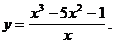
5. Используя формулы производной произведения или частного, найти производную функции:
1) 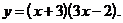
2) 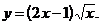
3) 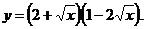
4) 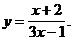
5) 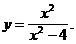
6) 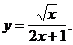
6. Используя правило дифференцирования сложной функции, найти производную функции:
1) 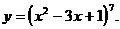
2) 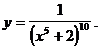
3) 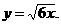
4) 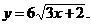
5) 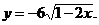
6) 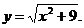
7) 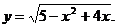
7. Найти критические точки функции:
1) 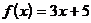
2) 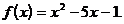
3) 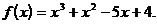
4) 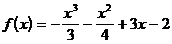
5) 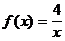
6) 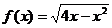
8. Найти промежутки возрастания и убывания функции:
1) 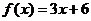
2) 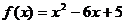
3) 
4) 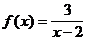
5) 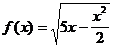
9. Найти точки экстремума и экстремумы функции.
1) 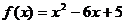
2) 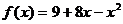
3) 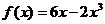
4) 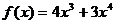
5) 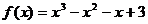
6) 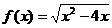
10. Найти наибольшее и наименьшее значения функции на промежутке.
1) 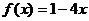 на [-3; 2]
на [-3; 2]
2) 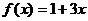 на [-2; 3)
на [-2; 3)
3) 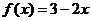 на (-1; 2]
на (-1; 2]
4) 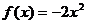 на [-2; 1]
на [-2; 1]
5) 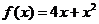 на [-1; 0]
на [-1; 0]
6) 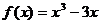 на [0; 3]
на [0; 3]
Решение задач раздела I.
1.
1) 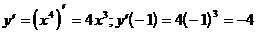
2) 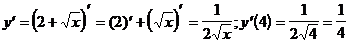
3) 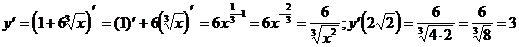
4) 
5) 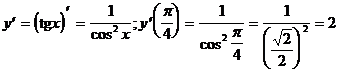
6) 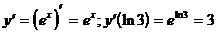
7) 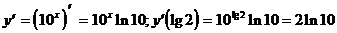
8) 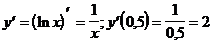
9) 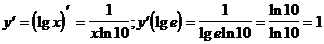
2.
10) 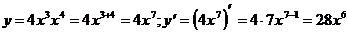
11) 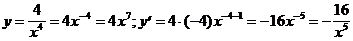
12) 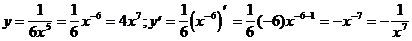
13) 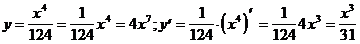
3.
1) 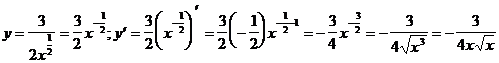
2) 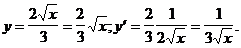
3) 
4) 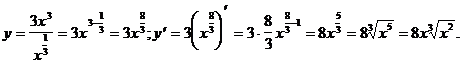
5) 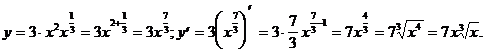
4.
1) 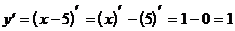
2) 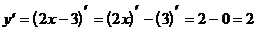
3) 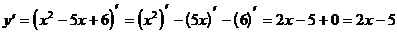
4) 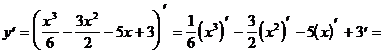
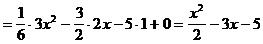
5) 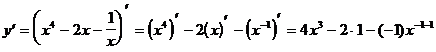
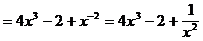
6) 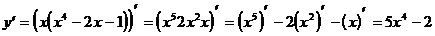
7) 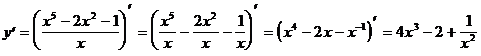
5.
1) 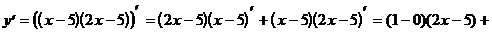
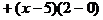
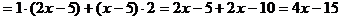
2) 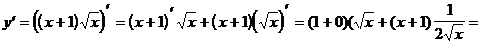
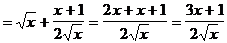
3) 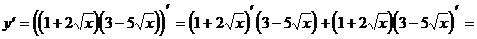
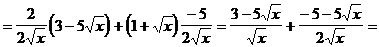
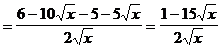
4) 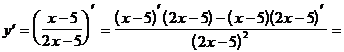
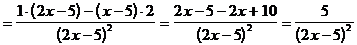
5) 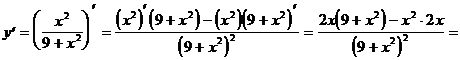
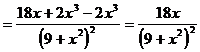
6) 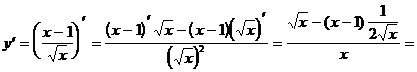
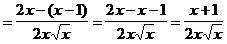
6.
1) 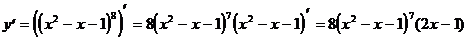
2) 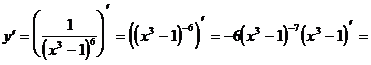

3) 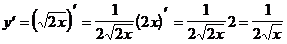
4) 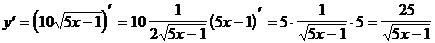
5) 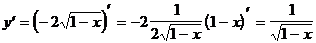
6) 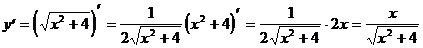
7) 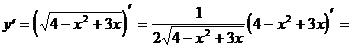
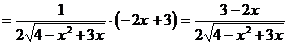
7.
1) О.О.Ф. xÎR; 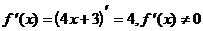 для всех x Î R. Ответ: критических точек нет.
для всех x Î R. Ответ: критических точек нет.
2) О.О.Ф. xÎR; 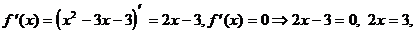
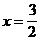 Î О.О.Ф.
Î О.О.Ф.
Ответ: 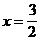 .
.
3) О.О.Ф. xÎR; 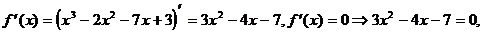 D = 16 + 84 = 100>0;
D = 16 + 84 = 100>0; 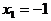 Î О.О.Ф.,
Î О.О.Ф., 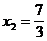 Î О.О.Ф. Ответ:
Î О.О.Ф. Ответ: 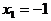 ,
, 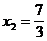
4) О.О.Ф. xÎR; 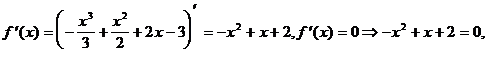
D = 1+8=9>0; 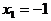 Î О.О.Ф.,
Î О.О.Ф., 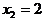 Î О.О.Ф. Ответ:
Î О.О.Ф. Ответ: 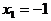 ,
, 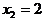
5) О.О.Ф. x¹ 0; 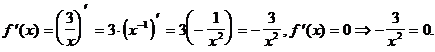
При х = 0 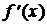 не существует. х = 0 Ï О.О.Ф. Ответ: критических точек нет.
не существует. х = 0 Ï О.О.Ф. Ответ: критических точек нет.
6) О.О.Ф. 2 х - х2 ³ 0; х (2- х)³0 Þ 0£ х £ 2.
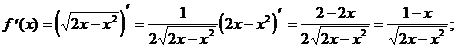
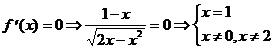
При х = 1 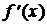 =0. При х = 0 и х = 2
=0. При х = 0 и х = 2 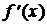 не существует.
не существует.
х 1 = 1 Î О.О.Ф., х 2 = 0 Î О.О.Ф., х 3 = 2 Î О.О.Ф. Ответ: х 1 = 1, х 2 = 0, х 3 = 2.
8.
1) О.О.Ф.: х Î R; 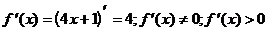 для всех х Î R.
для всех х Î R.
Ответ: возрастает для всех х Î R.
2) О.О.Ф.: х Î R; 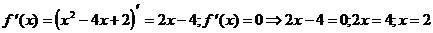 ÎО.О.Ф.
ÎО.О.Ф.
 Ответ: убывает на (-¥; 2)
Ответ: убывает на (-¥; 2)
возрастает на (2; +¥)
3) О.О.Ф.: х Î R; 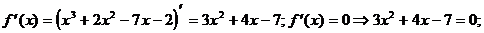 D= 16+84=100>0; х 1 = -7/3 Î О.О.Ф., х 2 = 1 Î О.О.Ф.
D= 16+84=100>0; х 1 = -7/3 Î О.О.Ф., х 2 = 1 Î О.О.Ф.
 Ответ: возрастает на (-¥; -7/3), (1; +¥)
Ответ: возрастает на (-¥; -7/3), (1; +¥)
убывает на (-7/3; 1)
4) О.О.Ф.: х ¹ 1; 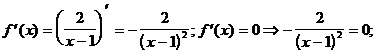
При х = 1 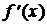 не существует х = 1 ÎО.О.Ф.
не существует х = 1 ÎО.О.Ф.
 Ответ: убывает на (-¥; 1), (1; +¥)
Ответ: убывает на (-¥; 1), (1; +¥)
5) О.О.Ф.: 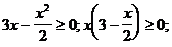 0£ х £6.
0£ х £6.
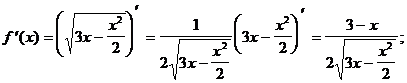
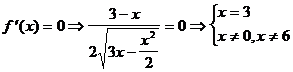
При х = 3ÎО.О.Ф. 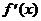 =0. При х = 0ÎО.О.Ф., х = 6ÎО.О.Ф.
=0. При х = 0ÎО.О.Ф., х = 6ÎО.О.Ф. 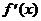 не существует.
не существует.

Ответ: возрастает на (0; 3),
убывает на (3; 6).
9.
1) О.О.Ф.: х Î R; 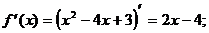
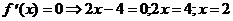 ÎО.О.Ф.
ÎО.О.Ф.

хmin = 2; уmin = y(xmin) = у (2) = 22-4×2+3=4-8+3=-1.
Ответ: хmin = 2;
уmin = -1.
2) О.О.Ф.: х Î R; 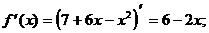
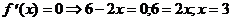 ÎО.О.Ф.
ÎО.О.Ф.

хmax = 3; уmax = y(xmax) = у (3) = 7+6×3-32=7+18-9=16
Ответ: хmax = 3;
уmax = 16
3) О.О.Ф.: х Î R; 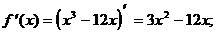
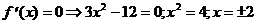 ÎО.О.Ф.
ÎО.О.Ф.

хmax = -2; уmax = y(xmax) = у (-2) = (-2)3-12×(-2)=-8+24=6
хmin = 2; уmin = y(xmin) = у (2) = 23-12×(2)=8-24=-6.
Ответ: хmax = -2; уmax =6
хmin = 2; уmin =-6.
4) О.О.Ф.: х Î R; 
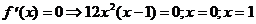 ÎО.О.Ф
ÎО.О.Ф

хmin = 1; уmin = y(xmin) = у (1) = 3×14-4×13=3-4=-1.
Ответ: хmin = 1; уmin =-1.
5) О.О.Ф.: х Î R; 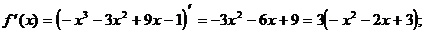
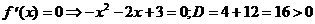 х 1 =-3ÎО.О.Ф., х 2 =1ÎО.О.Ф
х 1 =-3ÎО.О.Ф., х 2 =1ÎО.О.Ф

хmin




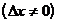 , то значение функции изменяется от
, то значение функции изменяется от 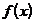 до
до 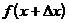 .
.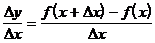
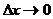 (если этот предел существует)
(если этот предел существует)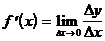 ,
,
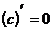
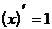
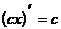
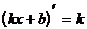
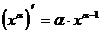
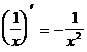
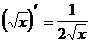
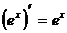
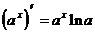
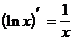
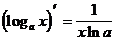
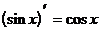
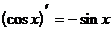
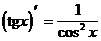
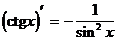
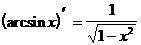
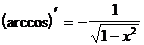
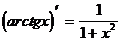
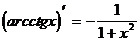
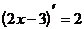 (формула 4)
(формула 4)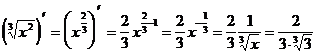 (формула 5)
(формула 5)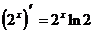 (формула 9)
(формула 9)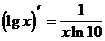 (формула 11)
(формула 11)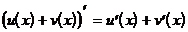
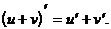 (1)
(1)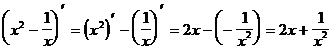
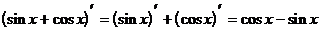
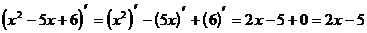
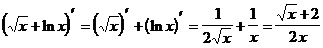
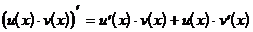
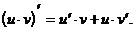 (2)
(2)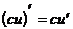 (3)
(3)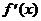 :
: 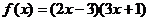 .
.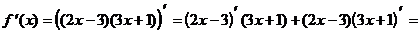
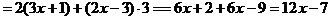 .
.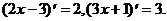
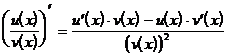
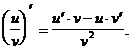 (4)
(4)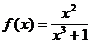 в точке х = 1:
в точке х = 1: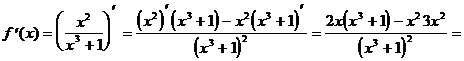

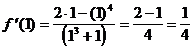
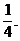
 в некоторой фиксированной точке x. Для этого нужно:
в некоторой фиксированной точке x. Для этого нужно: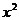 ;
;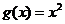 , а затем
, а затем 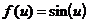 , аргумент u (u =g(x))в этом случае называют промежуточным, а x – независимой переменной.
, аргумент u (u =g(x))в этом случае называют промежуточным, а x – независимой переменной.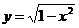 . Чтобы найти значение этой функции в фиксированной точке х, нужно сначала найти значение функции g(x) = 1 - x2, а потом найти значение
. Чтобы найти значение этой функции в фиксированной точке х, нужно сначала найти значение функции g(x) = 1 - x2, а потом найти значение 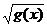 . В этом примере
. В этом примере 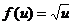 , где u = 1 - x 2.
, где u = 1 - x 2.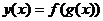 , если
, если 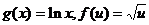 .
.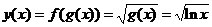 .
.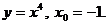
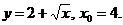

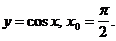
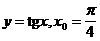
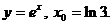
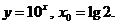
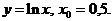
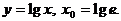
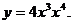 3)
3) 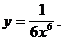
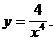 4)
4) 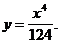
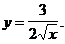
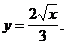
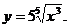
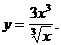
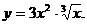
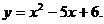
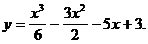
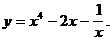
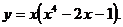
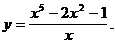
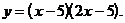
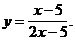
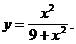
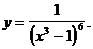
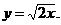
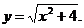
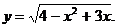
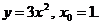
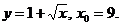
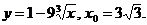
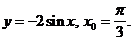
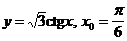
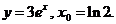
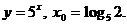
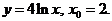
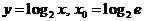
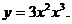
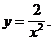
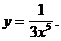
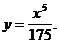
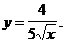
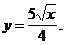
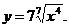
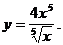
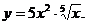
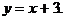
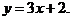
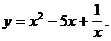
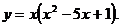
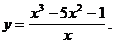
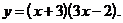
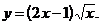
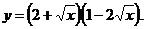
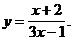
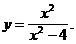
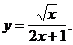
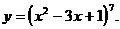
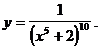
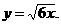
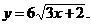
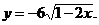
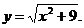
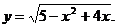
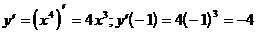
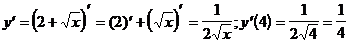
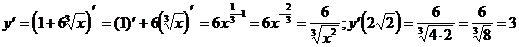

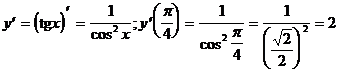
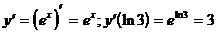
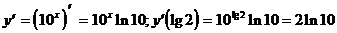
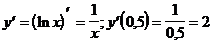
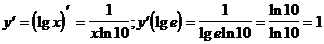
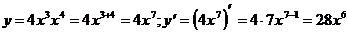
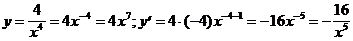
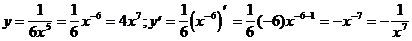
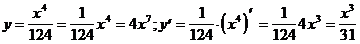
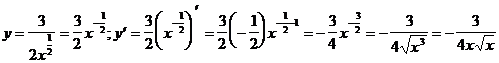
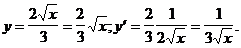

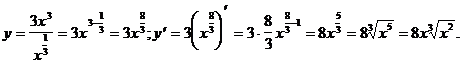
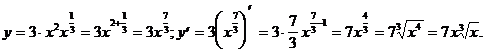
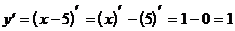
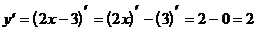
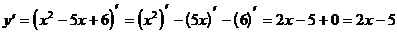
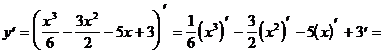
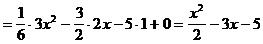
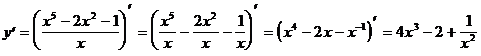
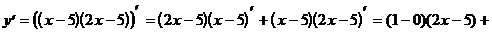
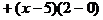
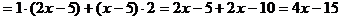
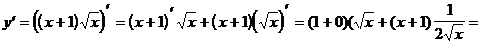
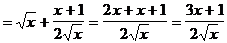
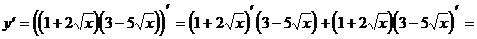
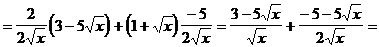
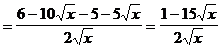
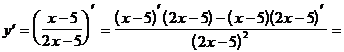
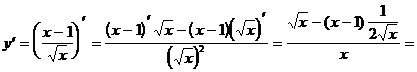
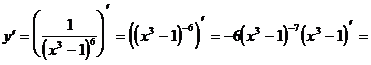

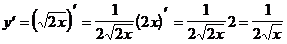
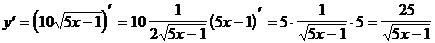
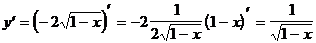
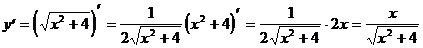
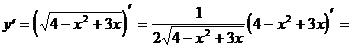
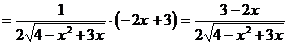
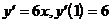 ;
;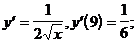
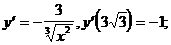

 ;
;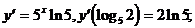
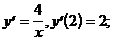
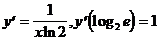 .
.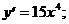 2)
2) 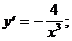 3)
3) 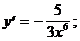 4)
4) 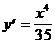 .
.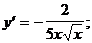 2)
2) 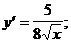 3)
3) 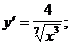 4)
4) 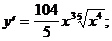 5)
5) 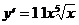 .
.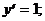
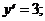
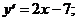
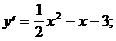
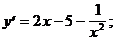
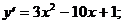
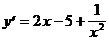 .
.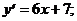
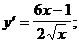
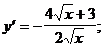
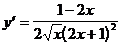 .
.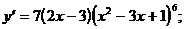
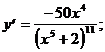
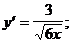
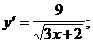
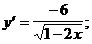
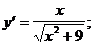
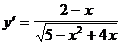 .
.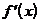 обращается в нуль или не существует, называются критическими точками этой функции.
обращается в нуль или не существует, называются критическими точками этой функции.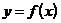 дифференцируема на промежутке (a;b) и возрастает (убывает) на нем, то ее производная
дифференцируема на промежутке (a;b) и возрастает (убывает) на нем, то ее производная 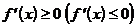 во всех точках этого промежутка.
во всех точках этого промежутка.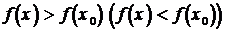 .
.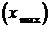 и минимума
и минимума 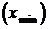 функции объединяются общим термином – точки экстремума.
функции объединяются общим термином – точки экстремума.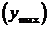 и минимумом
и минимумом 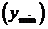 функции (или экстремумами самой функции).
функции (или экстремумами самой функции).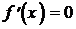 .
.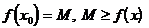
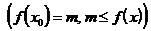 для всех x из этого промежутка.
для всех x из этого промежутка.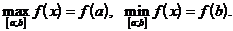
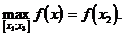
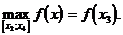
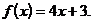
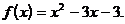
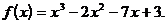
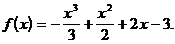
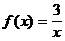
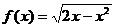
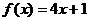
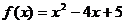
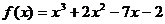
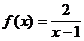
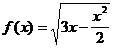
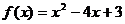
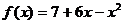
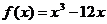
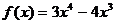
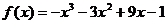
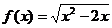
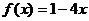 на [-3; 2]
на [-3; 2]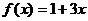 на [-2; 3)
на [-2; 3)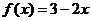 на (-1; 2]
на (-1; 2]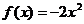 на [-2; 1]
на [-2; 1]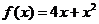 на [-1; 0]
на [-1; 0]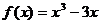 на [0; 3]
на [0; 3]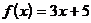
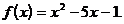
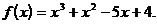
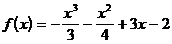
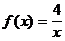
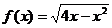
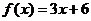
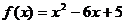

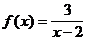
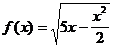
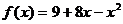
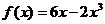
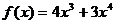
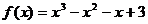
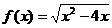
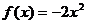 на [-2; 1]
на [-2; 1]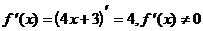 для всех x Î R. Ответ: критических точек нет.
для всех x Î R. Ответ: критических точек нет.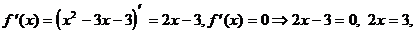
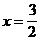 Î О.О.Ф.
Î О.О.Ф.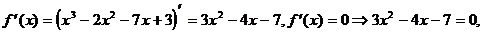 D = 16 + 84 = 100>0;
D = 16 + 84 = 100>0; 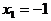 Î О.О.Ф.,
Î О.О.Ф., 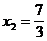 Î О.О.Ф. Ответ:
Î О.О.Ф. Ответ: 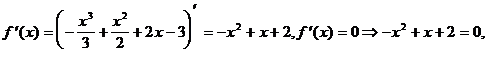
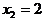 Î О.О.Ф. Ответ:
Î О.О.Ф. Ответ: 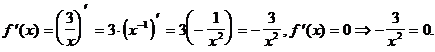
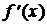 не существует. х = 0 Ï О.О.Ф. Ответ: критических точек нет.
не существует. х = 0 Ï О.О.Ф. Ответ: критических точек нет.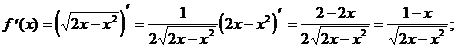
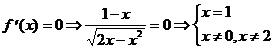
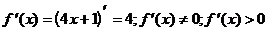 для всех х Î R.
для всех х Î R.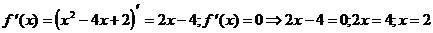 ÎО.О.Ф.
ÎО.О.Ф. Ответ: убывает на (-¥; 2)
Ответ: убывает на (-¥; 2)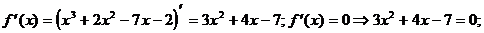 D= 16+84=100>0; х 1 = -7/3 Î О.О.Ф., х 2 = 1 Î О.О.Ф.
D= 16+84=100>0; х 1 = -7/3 Î О.О.Ф., х 2 = 1 Î О.О.Ф. Ответ: возрастает на (-¥; -7/3), (1; +¥)
Ответ: возрастает на (-¥; -7/3), (1; +¥)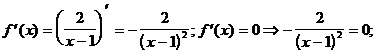
 Ответ: убывает на (-¥; 1), (1; +¥)
Ответ: убывает на (-¥; 1), (1; +¥)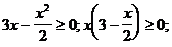 0£ х £6.
0£ х £6.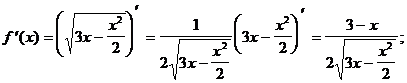
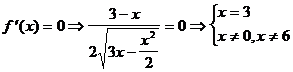

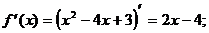
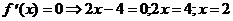 ÎО.О.Ф.
ÎО.О.Ф.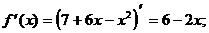
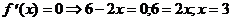 ÎО.О.Ф.
ÎО.О.Ф.
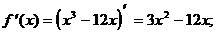
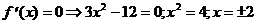 ÎО.О.Ф.
ÎО.О.Ф.

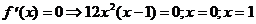 ÎО.О.Ф
ÎО.О.Ф
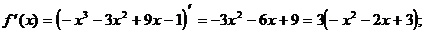
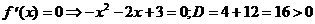 х 1 =-3ÎО.О.Ф., х 2 =1ÎО.О.Ф
х 1 =-3ÎО.О.Ф., х 2 =1ÎО.О.Ф


