Вторая основная задача динамики точки обратна первой, и заключается в том, чтобы по заданным силам, действующим на точку, определить ее движение.
Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.
Уравнение второго основного закона динамики для материальной точки массой m запишется в виде

где a – ускорение точки;
Fi – силы, действующие на точку, включая реакции связей.
Спроектировав уравнение (4.1) на декартовы оси координат, получим систему из трех уравнений

где ax, ay, az – проекции ускорения точки на декартовы оси координат;
Fx , Fy , Fz – проекция i -й силы на соответствующую ось.
Учитывая, что

получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки или второго порядка относительно координат точки.
Спроектировав уравнение (4.1) на естественные оси координат, получим следующую систему уравнений:
maτ = ΣFτi
man = ΣFni
0 = ΣFbi
Учитывая, что

где V – алгебраическое значение скорости точки, получим

0 = ΣFbi
В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых, или в естественных координатах.
Каждое дифференциальное уравнение дает целый класс решений, отличающихся друг от друга на некоторую постоянную величину.
Чтобы получить решение конкретной задачи, должны быть заданы так называемые начальные условия, которые позволяют определить постоянные интегрирования.
18. Механическая система. Масса системы. Центр масс системы, его координаты, скорость и ускорение. Моменты инерции механической системы и твердого тела. Радиус инерции. Осевые моменты инерции однородного тонкого стержня, тонкого круглого кольца и круглого диска (цилиндра). Теорема Штейнера-Гюйгенса о моментах инерции относительно параллельных осей.
Механическая система
Под механической системой в механике понимается совокупность материальных точек (тел), движения которых взаимосвязаны между собой.
Система материальных точек, движение которых не ограничено никакими связями, называется системой свободных материальных точек (примером являются планеты солнечной системы, движение которых по орбитам определяется действующими на них силами).
Определяющим признаком механической системы является наличие сил взаимодействия между отдельными материальными точками (телами) системы.
Действие связей на точки (элементы) механической системы выражается силами, называемыми реакциями связей. Поэтому все силы, действующие на систему несвободных точек, можно разделить на две группы: задаваемые (активные) силы и реакции связей. В то же время все силы, действующие на точки любой механической системы (свободной или несвободной), можно подразделить и по другому признаку: на внешние и внутренние силы.
Внешними называются силы, действующие на точки (тела) системы со стороны материальных точек (тел), не входящих в состав данной механической системы.
Внутренними называются силы взаимодействия между материальными точками (телами) данной механической системы.
Одна и та же сила может быть как внешней, так и внутренней, в зависимости от того, какая механическая система рассматривается. Так, например, реакции подшипников вала являются внешними силами относительно вала. Эти же реакции относятся к внутренним силам, когда рассматривается вся установка.
Рассмотрим механическую систему, состоящую из k материальных точек (тел) M1,M2,M3,...Mk c соответствующими массами m1,m2,m3,...,mk (рисунок 1.1).

Рисунок 1.1
Введем следующие определения:
- mj × rj - статический момент массы материальной точки относительно центра (полюса) О;
- ∑mj × rj - статический момент массы механической системы относительно центра (полюса);
- ∑mj =M - масса механической системы (арифметическая сумма масс точек системы).
· Центр масс механической системы
· Центром масс механической системы называется такая геометрическая точка C, концентрируя в которой (мысленно) массу M всей механической системы, получим, что ее статический момент массы равен статическому моменту массы всей механической системы, т.е.
· M × rc = ∑mj × rj (1.1)
· Отсюда
· 
· Проецируя обе части равенства (1.2) на оси координат, получаем аналитические формулы для координат центра масс механической системы:
· 
· Выражению (1.2) можно придать и другой вид, если умножить числитель и знаменатель ее правой части на ускорение силы тяжести. В этом случае
· 
· где Pj = mj ∙ g (j = 1,2,3,...,n) – веса материальных точек, образующих механическую систему;
∑Pj = M ∙ g = G – вес всей механической системы.
· Выражение (1.4) определяет радиус-вектор центра тяжести неизменяемой материальной системы в предположении, что она находится в поле силы тяжести.
· Отсюда следует, что центр тяжести неизменяемой (жесткой) механической системы (в частности твердого тела) совпадает с центром масс.
· Однако понятия о центре масс и центре тяжестимеханической системы не являются тождественными. Понятие о центре тяжести как о точке, через которую проходит линия действия равнодействующей сил тяжести, по существу имеет смысл только для твердого тела, находящегося в однородном поле тяжести.
· Понятие же о центре масс как о характеристике распределения масс в механической системе является более широким, так как имеет смысл для любой механической системы независимо от того, находится ли данная система под действием каких-либо сил или нет. Поэтому понятие центра тяжести можно рассматривать как частный случай по отношению к понятию центра масс.
· В общем случае следует говорить о центре масс материальной (механической) системы, а не о центре тяжести. При определении центра масс материальной системы можно пользоваться методами, установленными в статике для определения центра тяжести (метод симметрии, метод расчленения на простейшие элементы, метод отрицательных масс и т.д.).
Момент инерции тела относительно оси. Радиус инерции.
Положение центра масс характеризует распределение масс системы не полностью. Например (рис.3 ), если расстояния h от оси Oz каждого из одинаковых шаров А и В увеличить на одну и ту же величину, то положение центра масс системы не изменится, а распределение масс станет другим, и это скажется на движении системы (вращение вокруг оси Oz при прочих равных условиях будет происходить медленнее).

Рис.3
Поэтому в механике вводится еще одна характеристика распределения масс - момент инерции. Моментом инерции тела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси
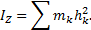
Момент инерции имеет размерность [кг∙м2]
Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.
Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.
Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является мерой инертности тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.
Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси. Для одной материальной точки, находящейся на расстоянии h от оси,  .
.
Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина  , определяемая равенством
, определяемая равенством
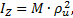
где М - масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
В случае сплошного тела, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве  , обратится в интеграл. В результате, учитывая, что
, обратится в интеграл. В результате, учитывая, что  , где
, где 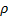 - плотность, а V - объем тела, получим
- плотность, а V - объем тела, получим
 или
или 
Интеграл здесь распространяется на весь объем V тела, а плотность 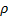 и расстояние h зависят от координат точек тела.
и расстояние h зависят от координат точек тела.
Моменты инерции некоторых однородных тел:
1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относительно оси Аz, перпендикулярной к стержню и проходящей через его конец А (рис.4).

Рис.4
Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h=x, а масса  , где
, где  - масса единицы длины стержня. В результате
- масса единицы длины стержня. В результате

Заменяя здесь ρ1его значением, найдем окончательно:

А момент инерции тонкого однородного стержня длины l и массы М относительно оси проходящего через середину и перпендикулярную стержню равен

2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис.4, а). Так как все точки кольца находятся от оси Cz на расстоянии hk=R, то

Следовательно, для кольца 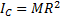 .
.
Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относительно ее оси.
3. Круглая однородная пластина или цилиндр радиуса R и массы М. Вычислим момент инерции круглой пластины относительно оси Сz, перпендикулярной к пластине и проходящей через ее центр (см. рис.5, а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.5, б).



Рис.5
Площадь этого кольца равна  , а масса
, а масса  где
где  - масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
- масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
 ,
,
а для всей пластины  . Заменяя здесь
. Заменяя здесь  его значением, найдем окончательно
его значением, найдем окончательно 
Такая же формула получится, очевидно, и для момента инерции  однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.5, в).
однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.5, в).
4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:
а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у - вдоль BD):

б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):

г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра):  .
.













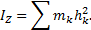
 .
. , определяемая равенством
, определяемая равенством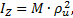
 , обратится в интеграл. В результате, учитывая, что
, обратится в интеграл. В результате, учитывая, что  , где
, где 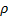 - плотность, а V - объем тела, получим
- плотность, а V - объем тела, получим или
или 

 , где
, где  - масса единицы длины стержня. В результате
- масса единицы длины стержня. В результате



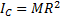 .
.


 , а масса
, а масса  где
где  - масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
- масса единицы площади пластины. Тогда для выделенного элементарного кольца будет ,
, . Заменяя здесь
. Заменяя здесь  его значением, найдем окончательно
его значением, найдем окончательно 
 однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.5, в).
однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.5, в).

 .
.


