 Пусть функция
Пусть функция 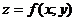 определена в области
определена в области 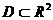
 , и функция z дифференцируема в точке
, и функция z дифференцируема в точке  , тогда
, тогда 
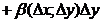 .
.
Определение. Производной функции 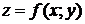 в точке
в точке 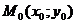 в направлении вектора
в направлении вектора 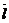 называется предел отношения приращения функции z в направлении вектора
называется предел отношения приращения функции z в направлении вектора 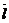 в точке
в точке  к
к
величине  , когда
, когда 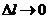 .
.
 где
где  - направляющие косинусы вектора
- направляющие косинусы вектора 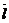 (они же координаты единичного вектора
(они же координаты единичного вектора  ).
).
Производная функции по направлению характеризует скорость изменения функции в точке 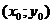 в направлении вектора
в направлении вектора 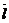 .
.
Пример. Найти производные функции  в точке
в точке  в направлении вектора
в направлении вектора  где
где 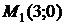 .
.
1) 
2) 

3)  В точке М функции возрастает в направлении вектора
В точке М функции возрастает в направлении вектора  .
.
Градиент функции.
Определение. Градиентом функции 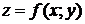 в точке
в точке 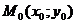 называется вектор с координатами равными частным производным функции z в точке
называется вектор с координатами равными частным производным функции z в точке  и обозначается
и обозначается 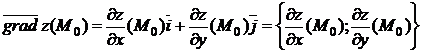 .
.
Градиент функции указывает направление наискорейшего роста функции, а максимальная скорость роста функции равна модулю градиента.
Скалярное произведение 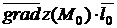 равно производной функции по направлению
равно производной функции по направлению 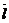 в точке
в точке  . Действительно
. Действительно 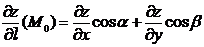
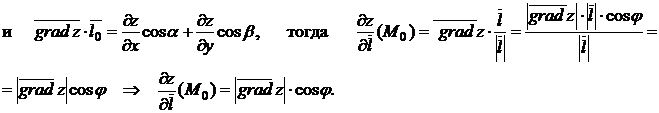 Величина в правой части принимает наибольшее значение при
Величина в правой части принимает наибольшее значение при 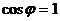 , т.е. когда
, т.е. когда 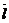 совпадает по направлению с
совпадает по направлению с 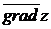 . В свою очередь частные производные функции
. В свою очередь частные производные функции 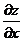 и
и 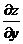 является производными функции z в направлении координатных осей OX и OY.
является производными функции z в направлении координатных осей OX и OY.
 ;
;
 .
.
Экстремумы функции двух переменных. Необходимое и достаточное условия существования экстремумов.
Пусть функция 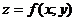 определена на множестве
определена на множестве 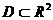 , точка
, точка  является внутренней точкой множества D (принадлежит ему вместе с некоторой окрестностью)
является внутренней точкой множества D (принадлежит ему вместе с некоторой окрестностью)
Определение. Точка 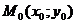 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции 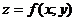 , если существует окрестность точки
, если существует окрестность точки  , для всех точек которой
, для всех точек которой  при
при  (
( ).
).
Точки локального максимума и локального минимума называются точками экстремума функции.
Теорема (необходимое условие экстремумов).
Если функция 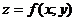 в точке
в точке  имеет экстремум и в точке
имеет экстремум и в точке 
существуют частные производные функции z, то эти частные производные
равны нулю, то есть  .
.
Замечание. Обратное утверждение к теореме, вообще говоря, неверно. Из
того, что  ещё не следует, что
ещё не следует, что  - точка экстремума. Это точка лишь "подозрительная" на экстремум. Такие точки называют стационарными. Экстремумы функции могут находиться либо в стационарных точках, либо в точках, где частные производные не существуют.
- точка экстремума. Это точка лишь "подозрительная" на экстремум. Такие точки называют стационарными. Экстремумы функции могут находиться либо в стационарных точках, либо в точках, где частные производные не существуют.
Теорема. (достаточное условие существование экстремума)
Пусть функция 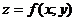 имеет непрерывные производные второго порядка в некоторой окрестности стационарной точки
имеет непрерывные производные второго порядка в некоторой окрестности стационарной точки 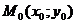 , тогда, если
, тогда, если  , то
, то  - точка экстремума, причем при
- точка экстремума, причем при  в точке
в точке  локальный минимум, при
локальный минимум, при  -
-
локальный максимум; если 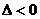 , то
, то  - не является точкой экстремума.
- не является точкой экстремума.
Замечание. Если  , то вопрос о существовании экстремума в точке
, то вопрос о существовании экстремума в точке  остается открытым (используются другие методы исследования).
остается открытым (используются другие методы исследования).
Пример. Найти экстремумы функции 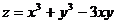


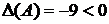 , значит в точке А экстремума нет;
, значит в точке А экстремума нет;  и
и 
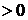 , значит в точке В локальный минимум
, значит в точке В локальный минимум 
Лекция 8. Метод наименьших квадратов.
Метод наименьших квадратов



 Пусть функция
Пусть функция 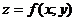 определена в области
определена в области 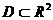
 , и функция z дифференцируема в точке
, и функция z дифференцируема в точке  , тогда
, тогда 
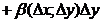 .
. в точке
в точке 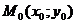 в направлении вектора
в направлении вектора 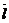 называется предел отношения приращения функции z в направлении вектора
называется предел отношения приращения функции z в направлении вектора  , когда
, когда 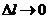 .
. где
где  - направляющие косинусы вектора
- направляющие косинусы вектора  ).
).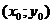 в направлении вектора
в направлении вектора  в точке
в точке  в направлении вектора
в направлении вектора  где
где 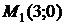 .
.


 В точке М функции возрастает в направлении вектора
В точке М функции возрастает в направлении вектора  .
.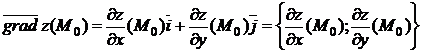 .
.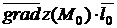 равно производной функции по направлению
равно производной функции по направлению 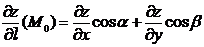
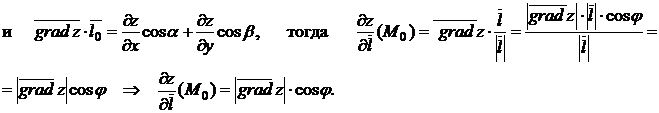 Величина в правой части принимает наибольшее значение при
Величина в правой части принимает наибольшее значение при 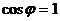 , т.е. когда
, т.е. когда 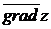 . В свою очередь частные производные функции
. В свою очередь частные производные функции 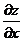 и
и 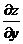 является производными функции z в направлении координатных осей OX и OY.
является производными функции z в направлении координатных осей OX и OY. ;
; .
. является внутренней точкой множества D (принадлежит ему вместе с некоторой окрестностью)
является внутренней точкой множества D (принадлежит ему вместе с некоторой окрестностью) при
при  (
( ).
). .
. ещё не следует, что
ещё не следует, что  , то
, то  в точке
в точке  -
-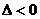 , то
, то  , то вопрос о существовании экстремума в точке
, то вопрос о существовании экстремума в точке 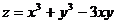


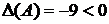 , значит в точке А экстремума нет;
, значит в точке А экстремума нет;  и
и 
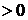 , значит в точке В локальный минимум
, значит в точке В локальный минимум 


