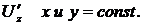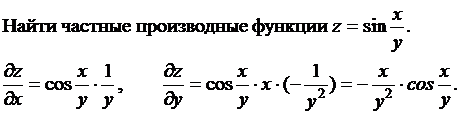Пусть
Пусть  определена на
определена на 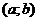 ,
,  .
.
 График
График  называется выпуклым в точке
называется выпуклым в точке  , если кривая
, если кривая 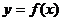 лежит под касательной в точке
лежит под касательной в точке  .
.
График называется вогнутым в точке  , если кривая
, если кривая 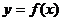 лежит над касательной в точке
лежит над касательной в точке  .
.
Теорема (достаточное условие выпуклости и вогнутости графика функции). Пусть  имеет непрерывную вторую производную на
имеет непрерывную вторую производную на 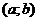 , тогда: если
, тогда: если 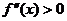 для каждого
для каждого  , то
, то  вогнутая на
вогнутая на 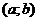 ; если
; если  для каждого
для каждого  , то
, то  выпуклая на
выпуклая на 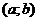 .
.
Определение. Точки графика функции, которые отделяют выпуклую часть
графика от вогнутой, называются точками перегиба.
 В точках перегиба касательная к графику функции пересекает его с обеих сторон, с одной стороны график лежит над касательной, с другой - под касательной.
В точках перегиба касательная к графику функции пересекает его с обеих сторон, с одной стороны график лежит над касательной, с другой - под касательной.
Теорема 1. (необходимое условие существования точки перегиба).
Пусть 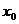 - абсцисса точки перегиба графика функции
- абсцисса точки перегиба графика функции  и
и  дважды дифференцируема в точке
дважды дифференцируема в точке 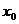 , тогда
, тогда 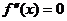 .
.
 Замечание. Обратное утверждение к теореме, вообще говоря, неверно. Из того, что
Замечание. Обратное утверждение к теореме, вообще говоря, неверно. Из того, что 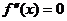 ещё не следует, что
ещё не следует, что  - абсцисса точки перегиба. Например, для функции
- абсцисса точки перегиба. Например, для функции  ,
,  ,
,  и
и  при
при  , но точка (0;0) не является точкой перегиба функции
, но точка (0;0) не является точкой перегиба функции  .
.
Теорема 2. (достаточное условие существования точки перегиба). Пусть функция  непрерывна в некоторой окрестности точки
непрерывна в некоторой окрестности точки 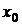 и дважды дифференцируема в этой окрестности, кроме, может быть, самой этой точки
и дважды дифференцируема в этой окрестности, кроме, может быть, самой этой точки 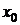 , тогда: если при переходе через точку
, тогда: если при переходе через точку 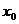
 меняет свой знак, то
меняет свой знак, то 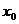 - абсцисса точки перегиба; если при переходе через точку
- абсцисса точки перегиба; если при переходе через точку 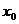
 не меняет знак, то
не меняет знак, то 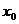 не является абсциссой точкой перегиба.
не является абсциссой точкой перегиба.
Асимптоты графика функции.
Определение. Прямая линия l называется асимптотой графика функции 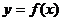 , если расстояние от текущей точки кривой до этой прямой стремится к нулю при неограниченном удалении текущей точки кривой от начала координат.
, если расстояние от текущей точки кривой до этой прямой стремится к нулю при неограниченном удалении текущей точки кривой от начала координат.
Асимптоты бывают двух видов: вертикальные и наклонные.
Вертикальные асимптоты имеют уравнение 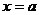 , при этом хотя бы один из пределов функции при
, при этом хотя бы один из пределов функции при 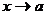 должен быть равен
должен быть равен 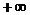 или
или 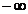 . Вертикальные асимптоты ищут на границах области определения функции и в точках бесконечного разрыва функции.
. Вертикальные асимптоты ищут на границах области определения функции и в точках бесконечного разрыва функции.
Наклонные асимптоты имеют уравнение 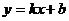 . Их ищут по двум направлениям при
. Их ищут по двум направлениям при 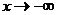 ,
, 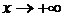 по формулам
по формулам
 ,
, 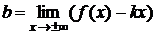 .
.
Частным видом наклонных асимптот являются горизонтальные асимптоты, которые имеют место при 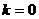 .
.
Уравнение горизонтальных асимптот 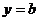 . Если хотя бы один из пределов для нахождения k или b не существует, или бесконечен, то наклонных асимптот в данном направлении нет.
. Если хотя бы один из пределов для нахождения k или b не существует, или бесконечен, то наклонных асимптот в данном направлении нет.
Схема нахождения асимптот:
1) найти область определения функции;
2) найти вертикальные асимптоты на основе области определения;
3) найти наклонные асимптоты по формулам для вычисления k и b при 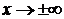 .
.
Лекция 6. Функции многих переменных.
6.1. Определение функции двух переменных, область определения функции, график функции.
Определения предела и непрерывности функции двух переменных. Свойства непрерывных функций.
Частные производные.
6.1. Определение функции двух переменных, область определения функции, график функции.
Для упрощения ограничимся рассмотрением функции двух переменных. Все дальнейшее справедливо и для функции многих переменных.
Определение. Если по какому-либо закону или правилу каждой паре 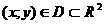 независимых переменных ставится в соответствие вполне определенное значение z, то говорят, что на множестве D определена функция двух переменных
независимых переменных ставится в соответствие вполне определенное значение z, то говорят, что на множестве D определена функция двух переменных 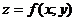 .
.
Область определения D функции двух переменных является некоторым подмножеством точек плоскости 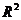 .
.
Определение. Графиком функции двух переменных 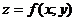 является множество точек пространства
является множество точек пространства 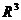 вида
вида 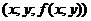 , где
, где 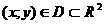 и D - область определения функции двух переменных.
и D - область определения функции двух переменных.
Определения предела и непрерывности функции двух переменных. Свойства непрерывных функций.
Пусть 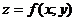 определена на множестве
определена на множестве 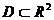 и точка
и точка 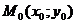 - предельная точка множества D (т.е. любая окрестность точки
- предельная точка множества D (т.е. любая окрестность точки  содержит точки множества D, отличные от точки
содержит точки множества D, отличные от точки  ). Расстояние между точками
). Расстояние между точками 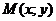 и
и 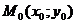 определяется по формуле
определяется по формуле 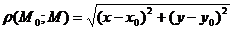 .
.
Определение. Число A называется пределом функции 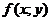 при
при
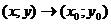 , если для любого положительного числа
, если для любого положительного числа 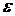 найдется число
найдется число 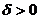 , зависящее от
, зависящее от 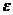 такое, что
такое, что 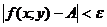 как только
как только 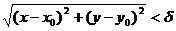 при
при 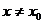 и
и 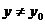 .
.
Замечание.
Неравенство 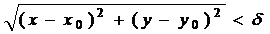 определяет
определяет 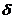 окрестность точки
окрестность точки 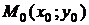 или множество точек
или множество точек 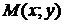 , расстояние которых до точки
, расстояние которых до точки 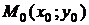 меньше
меньше 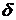 :
: 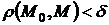 .
.
Все правила вычисления и свойства пределов для функции одной переменной справедливы для и функции двух переменных.
Определение. Функция 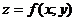 называется непрерывной в точке
называется непрерывной в точке  , если
, если
предел этой функции в точке  совпадает со значением функции в точке
совпадает со значением функции в точке  , то есть
, то есть 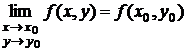 .
.
Придадим аргументам 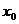 и
и 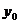 приращения
приращения 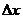 и
и 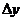 так, чтобы точки
так, чтобы точки 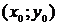 ,
, 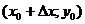 ,
, 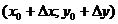 и
и 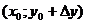 принадлежали области определения функции. Тогда:
принадлежали области определения функции. Тогда:
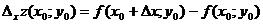 - частное приращение функции z по переменной x в точке
- частное приращение функции z по переменной x в точке 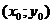 ;
;
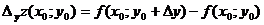 - частное приращение функции z по переменной y в точке
- частное приращение функции z по переменной y в точке 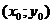 ;
;
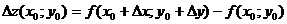 - полное приращение функции в точке
- полное приращение функции в точке 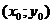 .
.
Определение. Функция 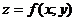 называется непрерывной в точке
называется непрерывной в точке 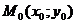 , если бесконечно малым приращениям аргументов соответствует бесконечно малое полное приращение функции, то есть
, если бесконечно малым приращениям аргументов соответствует бесконечно малое полное приращение функции, то есть 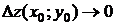 при
при 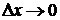 и
и 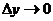 .
.
Данные определения непрерывности функции эквивалентны.
Свойства функций, непрерывных на ограниченном замкнутом множестве.
Теорема 1. Если функция 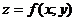 непрерывна на ограниченном замкнутом множестве, то она ограничена на этом множестве.
непрерывна на ограниченном замкнутом множестве, то она ограничена на этом множестве.
Теорема 2. Если функция 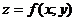 непрерывна на ограниченном замкнутом множестве, то на этом множестве она достигает своего наименьшего и наибольшего значений.
непрерывна на ограниченном замкнутом множестве, то на этом множестве она достигает своего наименьшего и наибольшего значений.
Теорема 3. Если функция 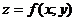 непрерывна на ограниченном замкнутом множестве и в двух точках этого множества принимают значения разных знаков, то на этом множестве найдется точка
непрерывна на ограниченном замкнутом множестве и в двух точках этого множества принимают значения разных знаков, то на этом множестве найдется точка 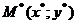 , в которой функция обращается в ноль, то есть
, в которой функция обращается в ноль, то есть 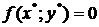 .
.
Частные производные.
Пусть функция 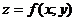 определена на множестве
определена на множестве 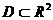 , точки
, точки 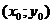 ,
, 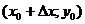 ,
, 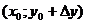 ,
, 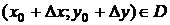 .
.
Определение. Частной производной функции 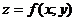 по переменной x в точке
по переменной x в точке 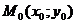 называется предел отношения частного приращения функции z по переменной x в точке
называется предел отношения частного приращения функции z по переменной x в точке  к приращению аргумента
к приращению аргумента 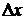 , когда
, когда 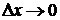 .
. 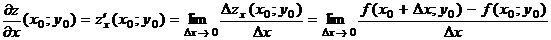 .
.
Определение. Частной производной функции 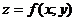 по переменной y в точке
по переменной y в точке 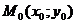 называется предел отношения частного приращения функции z по переменной y в точке
называется предел отношения частного приращения функции z по переменной y в точке  к приращению аргумента y, когда
к приращению аргумента y, когда 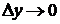 .
.
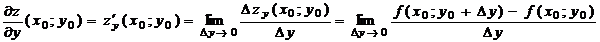 .
.
Замечание: 1) все правила дифференцирования функции одной переменной справедливы для функций многих переменных; 2) при нахождении частной производной функции по одной переменной все остальные переменные считают постоянными, то есть для функции 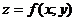 при вычислении
при вычислении 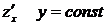 , при вычислении
, при вычислении 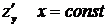 ; для функции
; для функции 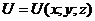 при вычисления
при вычисления 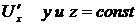 , при вычислении
, при вычислении 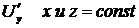 , при вычислении
, при вычислении 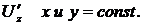
Пример.
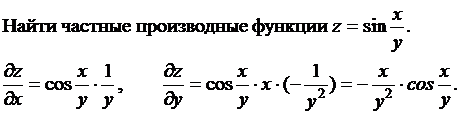



 Пусть
Пусть  определена на
определена на 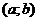 ,
,  .
. График
График  , если кривая
, если кривая 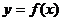 лежит под касательной в точке
лежит под касательной в точке 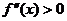 для каждого
для каждого  , то
, то  для каждого
для каждого  В точках перегиба касательная к графику функции пересекает его с обеих сторон, с одной стороны график лежит над касательной, с другой - под касательной.
В точках перегиба касательная к графику функции пересекает его с обеих сторон, с одной стороны график лежит над касательной, с другой - под касательной.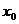 - абсцисса точки перегиба графика функции
- абсцисса точки перегиба графика функции 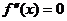 .
. Замечание. Обратное утверждение к теореме, вообще говоря, неверно. Из того, что
Замечание. Обратное утверждение к теореме, вообще говоря, неверно. Из того, что  - абсцисса точки перегиба. Например, для функции
- абсцисса точки перегиба. Например, для функции  ,
,  ,
,  и
и  при
при  , но точка (0;0) не является точкой перегиба функции
, но точка (0;0) не является точкой перегиба функции 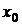 и дважды дифференцируема в этой окрестности, кроме, может быть, самой этой точки
и дважды дифференцируема в этой окрестности, кроме, может быть, самой этой точки 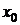 , тогда: если при переходе через точку
, тогда: если при переходе через точку  меняет свой знак, то
меняет свой знак, то 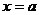 , при этом хотя бы один из пределов функции при
, при этом хотя бы один из пределов функции при 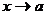 должен быть равен
должен быть равен 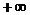 или
или 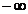 . Вертикальные асимптоты ищут на границах области определения функции и в точках бесконечного разрыва функции.
. Вертикальные асимптоты ищут на границах области определения функции и в точках бесконечного разрыва функции.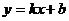 . Их ищут по двум направлениям при
. Их ищут по двум направлениям при 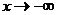 ,
, 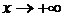 по формулам
по формулам ,
, 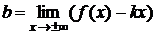 .
.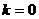 .
.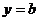 . Если хотя бы один из пределов для нахождения k или b не существует, или бесконечен, то наклонных асимптот в данном направлении нет.
. Если хотя бы один из пределов для нахождения k или b не существует, или бесконечен, то наклонных асимптот в данном направлении нет.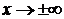 .
.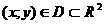 независимых переменных ставится в соответствие вполне определенное значение z, то говорят, что на множестве D определена функция двух переменных
независимых переменных ставится в соответствие вполне определенное значение z, то говорят, что на множестве D определена функция двух переменных 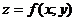 .
.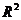 .
.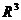 вида
вида 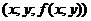 , где
, где 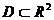 и точка
и точка 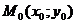 - предельная точка множества D (т.е. любая окрестность точки
- предельная точка множества D (т.е. любая окрестность точки  содержит точки множества D, отличные от точки
содержит точки множества D, отличные от точки 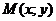 и
и 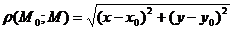 .
.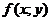 при
при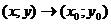 , если для любого положительного числа
, если для любого положительного числа 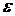 найдется число
найдется число 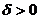 , зависящее от
, зависящее от 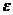 такое, что
такое, что 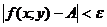 как только
как только 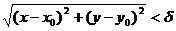 при
при 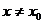 и
и 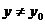 .
.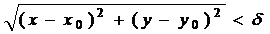 определяет
определяет 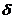 окрестность точки
окрестность точки 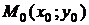 или множество точек
или множество точек 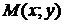 , расстояние которых до точки
, расстояние которых до точки 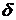 :
: 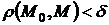 .
.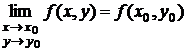 .
.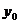 приращения
приращения 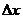 и
и 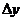 так, чтобы точки
так, чтобы точки 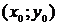 ,
, 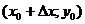 ,
, 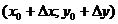 и
и 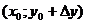 принадлежали области определения функции. Тогда:
принадлежали области определения функции. Тогда: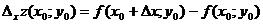 - частное приращение функции z по переменной x в точке
- частное приращение функции z по переменной x в точке 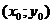 ;
;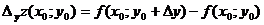 - частное приращение функции z по переменной y в точке
- частное приращение функции z по переменной y в точке 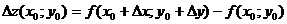 - полное приращение функции в точке
- полное приращение функции в точке 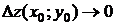 при
при 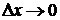 и
и 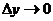 .
.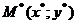 , в которой функция обращается в ноль, то есть
, в которой функция обращается в ноль, то есть 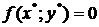 .
.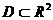 , точки
, точки 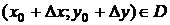 .
.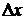 , когда
, когда 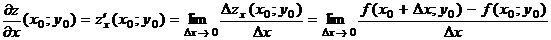 .
.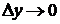 .
.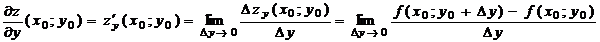 .
.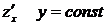 , при вычислении
, при вычислении 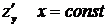 ; для функции
; для функции 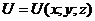 при вычисления
при вычисления 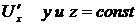 , при вычислении
, при вычислении 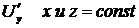 , при вычислении
, при вычислении