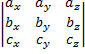Выберем в пространстве произвольную точку О, которую будем называть началом координат. Помести базисные вектора {i,j,k} своими началами в точку О. Через начало координат и базисные векторы проводим прямые, которые называются осями координат, причем прямая, проходящая через вектор i – ось ох (ось абсцисс), через j – оу (ось ординат), через k - ось oz (ось аппликат). Конец каждого базисного вектора отмечает на оси число 1.
Пусть М – произвольная точка пространства. Вектор 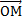 . Соединяющий начало координат с точкой М – радиус-вектор точки М. Вектор
. Соединяющий начало координат с точкой М – радиус-вектор точки М. Вектор 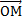 единственным образом разлагается по базису, т.е. существуют такие числа x,y,z что вектор
единственным образом разлагается по базису, т.е. существуют такие числа x,y,z что вектор 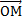 = x
= x 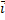 + y
+ y 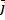 + z
+ z 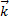 . Координатами точки М в прямоугольной системе координат Оxyz называются координаты вектора ОМ в базисе {i,j,k}.
. Координатами точки М в прямоугольной системе координат Оxyz называются координаты вектора ОМ в базисе {i,j,k}.
Для того, чтобы найчти координаты вектора, если известны координаты его начала и конца, нужно из координат конца вектора вычесть координаты его начала.
Направляющие косинусы вектора.
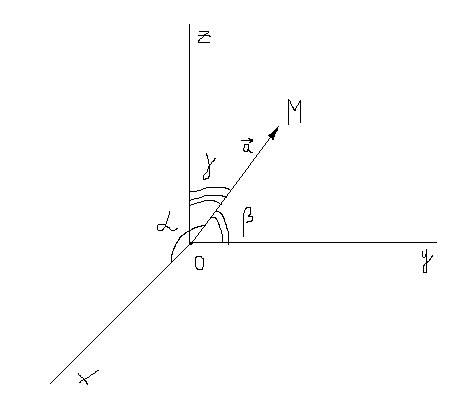
Пусть точка М(x,y,z); 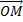 =
= 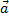
Пусть вектор а составляет с осями координат углы a, b, g. Косинусы этих углов – направляющие косинусы вектора а.
Пусть вектор а (ax,ay,az)
ax = Прi 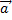 = |
= | 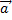 |cosa
|cosa
ay = Прj 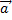 = |
= | 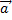 |cosb
|cosb
az = Прk 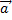 = |
= | 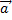 |cosg
|cosg
ð cosa = 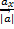 cosb=
cosb= 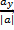 cosg=
cosg= 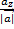
т.к. 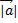 =
= 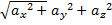
то cosa = 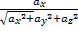
cosb = 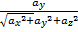
cosg = 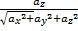
направляющие векторы обладают след св-вами:
1. cos2a+cos2b+cos2g=1
2. пусть 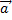 (ax,ay,az) – произвольный вектор. Требуется найти
(ax,ay,az) – произвольный вектор. Требуется найти 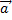 0 , который обладает след св-вами.
0 , который обладает след св-вами.
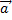 0
0 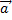 |
| 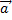 0 |=1
0 |=1
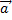 0 =
0 = 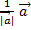
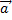 0 =
0 = 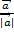 =
= 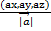
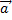 0 (
0 (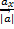 ,
, 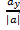 ,
, 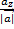 ) =>
) => 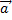 0 (cosa, cosb, cosg)
0 (cosa, cosb, cosg)
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Скалярным произведением 2х ненулевых векторов a, b называется число, равное произведению длин этих векторов и косинуса угла между ними. Обозначается 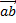 или (
или (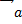 ,
, 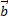 )
)
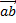 = |a||b|cosj
= |a||b|cosj
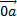 = 0
= 0
Из определения скалярного произведения 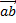 = |a|Прa
= |a|Прa 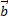 = |b|Прb
= |b|Прb 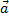
Свойства:
1. Ab = ba
2. (la)b = a(lb) = lab
3. a(b+c) = ab + ac
a(b+c) = |a|Прa 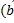 +c) = |a|(Прa
+c) = |a|(Прa 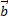 + |a|Прa
+ |a|Прa 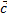 ) = ab + ac
) = ab + ac
4. aa = |a||a|cos0 = |a|2
5. ab = 0 ó a^b
вычисление скалярного произведения.
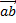 = axbx + ayby + azbz
= axbx + ayby + azbz
Применение скалярного пооизведения
1. вычисление углов cosj = 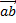 / |
/ | 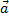 ||
|| 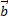 |
|
2. опрееление перпендикулярности 2х векторов 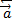 ^
^ 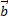
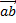 =0 или нет
=0 или нет
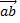 = |a|Прa
= |a|Прa 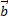 = |b|Прb
= |b|Прb 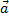 => Прb
=> Прb 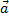 =
= 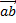 / |b|
/ |b|
3. в механике A = 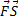 - работа силы
- работа силы
4. W = 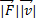
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Векторным произведением вектора а на вектор b называется третий вектор с.
c = [a, b] = a x b, удовлетворяющий условиям:
1. |c| = |a||b|sinj j - угол между a и b
2. c^a, c^b
3. {a, b, c} – правая тройка
Из определения модуля ясно, что |[a, b]| = |a||b|sinj = Sпараллелограмма
Свойства:
1. [a, a] = 0
2. [a, b] = - [b, a]
3. [a, b + c] = [a, b] + [a, c]
4. [aa, b] = [a, ab] = a[a, b]
5. [a, b] = 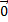 ó a||b
ó a||b
[a,b] = (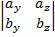 , -
, - 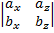 ,
, 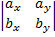 )
)
Применение векторного произведения
1. Вычисление площадей параллелограммов и треугольников. Sпаралл = |[a,b]|; Sтреуг = |[a,b]|/2
2. В физике
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ. КОМПЛАНАРНОСТЬ ТРЕХ ВЕКТОРОВ.
Смешанным произведением 3х векторов a,b,c называется число [a,b]c, полученное скалярным умножением векторного произведения [a,b] на третий вектор с. обозначается abc = (a,b,c) = [a,b]c
Пусть {a,b,c} – правая тройка.
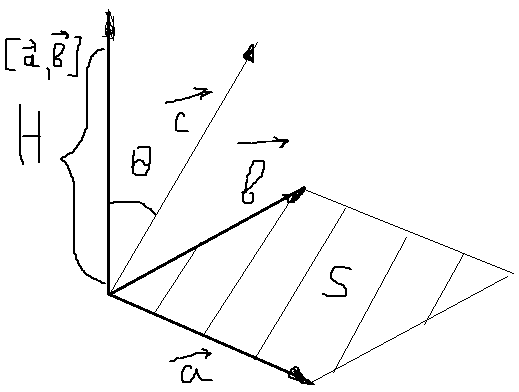
Тогда abc = [a,b]c = |[a,b]||c|cosq q - угол между [a,b] и c
abc = Sпараллелограмма|c|cosq = Sпараллелограмма H = V паралелипипеда, построенного на этиъ векторах.
Если {a,b,c} – левая тройка, то abc = -V
Свойства:
1. a[b,c] = [a,b]c
2. abc = cab = bca = -bac = -cab = -acb
3. (a1 + a2)bc = a1bc + a2bc
4. (aa)bc = a(ab)c = ab(ac) = aabc
Вычисление смешанного произведения
Пусть a(ax, ay, az) b(bx, by, bz) c(cx, cy, cz) abc -?
abc = [a,b]c = (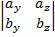 , -
, - 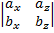 ,
, 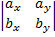 )(cx, cy, cz) = cx
)(cx, cy, cz) = cx 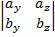 - cy
- cy 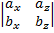 + cz
+ cz 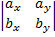 =
=
= 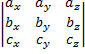
Т.е. abc = [a,b]c = 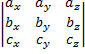
Формулировка: для того, чтобы 3 вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Необходимость: дано: 3 вектора компланарны, доказать: abc = 0
Если a,b,c компланарны, то [a,b]^c => abc = [a,b]c = 0
Достаточность. Дано: abc = 0, доказать: a,b,c – компланарны.
0 = abc = [a,b]c = |[a,b]||c|cosq = |a||b|sinj|c|socq = 0
1. |a| или |b| или |c| равны 0 => среди векторов есть нулевой вектор => a,b,c компланарны
2. sinj = 0 => a||b => a,b,c компланарны
3. cosq=0 => c^[a,b] = p/2 => с принадлежит плоскости ab
применение смешанного произведения
1. вычисление объемов параллелипипедов (V = |abc|), трегольных призм (V = |abc|/2), пирамид (V = |abc|/6)
2. определение компланарности трех векторов



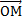 . Соединяющий начало координат с точкой М – радиус-вектор точки М. Вектор
. Соединяющий начало координат с точкой М – радиус-вектор точки М. Вектор 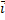 + y
+ y 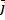 + z
+ z 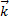 . Координатами точки М в прямоугольной системе координат Оxyz называются координаты вектора ОМ в базисе {i,j,k}.
. Координатами точки М в прямоугольной системе координат Оxyz называются координаты вектора ОМ в базисе {i,j,k}.
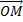 =
= 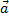
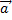 = |
= | 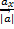 cosb=
cosb= 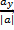 cosg=
cosg= 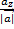
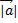 =
= 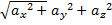
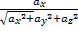
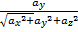
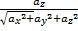
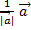
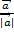 =
= 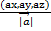
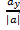 ,
, 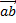 или (
или (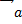 ,
, 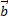 )
)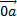 = 0
= 0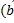 +c) = |a|(Прa
+c) = |a|(Прa 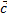 ) = ab + ac
) = ab + ac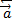 ^
^ 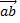 = |a|Прa
= |a|Прa 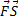 - работа силы
- работа силы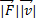
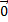 ó a||b
ó a||b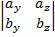 , -
, - 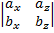 ,
, 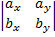 )
)