

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
В схеме независимых испытаний при больших n, формула Бернулли приводит к громоздким вычислениям. Задача, где рассматривается большое число n-независимых испытаний, а вероятность р- наступления события А в каждом испытании мала, может быть приближен вычислена вероятность Pn(m) по формуле Пуассона.
Теорема Пуассона: пусть вероятность события А при каждом испытании в серии из n-независимых испытаний =λ/n, где λ>0 –пост.независ. от n. Тогда вероятность Pn(m), при n→∞ и фикс. m, стремится к величине 
 -формула Пуассона
-формула Пуассона
Т.к. в таких испытаниях p-мало, то распределение Пуассона называют законом распределения редких явлений.
Pn(m)=Cnm*pm*qn~  =Pm(λ) - асимптотическая формула Пуассона
=Pm(λ) - асимптотическая формула Пуассона
Локальная предельная теорема Муавра-Лапласа.
Она устанавливает приближённую формулу для вычисления вероятности Pn(m).
Теорема: пусть вероятность события А в n-независимых испытаниях = р, (0<р<1), тогда вероятность Pn(m) того, что в этих испытаниях событие А наступит ровно m-раз удовлетворяет при n→∞ следующему соотношению: 
x= 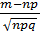
При больших n имеет место приближённая локальная формула Муавра-Лапласа.
Pn(m)~ 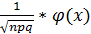 (25)
(25)
 (26)
(26)
Формула (25) даёт удовл.значение вероятности при достаточно больших значениях n, а также если р не слишком близка к 0 или 1 (эффективнее всего при р близких к 0,5). Функция 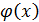 формулы (26) –чётная (
формулы (26) –чётная (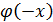 =
=  ), поэтому в прил. Приведены значения только для x>0.
), поэтому в прил. Приведены значения только для x>0.
Интегральная предельна теорема Муавра-Лапласа. Отклонение относительной частоты от постоянной вероятности в независимых испытаниях.
На практике при большом числе испытаний n и не слишком малой вероятности р важно оценить вероятность того, что число появлений события А лежит в некоторых границах. Эту оценку устанавливает интегральная теорема Муавра-Лапласа.
|
|
Теорема: пусть m-число наступлений события А в серии из n-независимых испытаний, р –вероятность наступления события А при каждом испытании (0<р<1), тогда вероятность Pn(m1≤m≤m2) того, что в этих испытаниях событие А появится не менее m1 раз и не более m2 раз, при n→∞ удовл. соотношению:
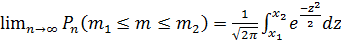
x1=  ; x2=
; x2= 
При больших значениях m имеет место приближённая интегральная формула Муавра-Лапласа: Pn(m1≤m≤m2)=Ф(х2)-Ф(х1) (27)
где Ф(х)= 
Эта функция называется функцией Лапласа, ё называют интегралом ошибок, она нечётная Ф(-х)= - Ф(х).
Используется в приложении для отрицательных значений х.
Замечание: оценка погрешности при использовании формулы (27) показывает, что хорошая точность обеспечивается уже при значениях npq≥10.
Вероятностью того, что в n независимых испытаниях, в каждом из которых вероятность появления события = р(0<р<1), абсолютная величина отклонения относительной частоты m/n появления события, от вероятности появления события, не привысит положительного числа ε и приближённо равна удвоенной функции Лапласа Х=ε 
P(| 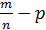 |≤ε)=2Ф(ε
|≤ε)=2Ф(ε 
|
|
|

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!