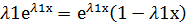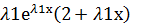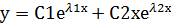Задачи, приводящие к дифференциальным уравнениям (ДУ). Основные сведения о ДУ (обыкновенные ДУ, ОДУ n-ого порядка, решение ДУ на интервале).
ДУ – ур-ния содержащие неизвестные функции или вектор функции под знаком производной или дифференциала.
1. dx/dt = -kx - уравнение радиоактивного распада, где k-постоянная распада, x- кол-во неразложившегося вещ-ва в момент времени t, dx/dt – скорость распада,которая пропорциональна кол-ву распада.
2. m*(d2r/dt2) = F(t,r,dr/dt) - ур-ние движения точки, массы m под влиянием силы F, зависящей от времени, положения точки радиус вектора и ее скорости.
3. ð2u/ ðx2 + ð2u/ ðy2+ ð2u/ ðz2 = 4πρ(x,y,z) - ур-ние Пуассона, которому удовлетворяет потенциал и (x,y,z) электростатического поля, ρ-плотность зарядов.
ДУ – ур-ние относительно неизвестной функции и ее производных различных порядков. Порядком ДУ называется порядок старшей производной входящей в это уровнение.
ДУ называется обыкновенным, если искомая функция зависит от одной переменной. (пример 1,2)Если искомая функция зависит от нескольких переменных, то ДУ называются ур-ниями с частными производными (пример 3).
Обыкновенные ДУ(ОДУ) n-ого порядка наз. ур-ния вида:F(x,y,y`,y``,…yn)=0, (1)
Где, x-независимая переменная, y=y(x) –зависимая от x-искомая ф-ия переменной x, y`,y``,…yn -производная, F() –заданная ф-ия своих аргументом,может не содержать несколько своих элементов,но должна зависить от yn.
Если ур-ние (1) разрешимо относительно производной n-ого порядка, то можно представить: yn = f(x, y,y`,y``,…yn-1). (2)
Ф-ия y=φ(x) определенная и непрерывная дифференцируемая n раз на (a,b) назыв. Решением ур-ния (1) в этом интервале если она обращает указанное ур-ние в тождество: F(x, φ(x), φ`(x),… φn(x)) =0, для всех х принадлеж. интервалу (a,b).
Задача Коши для ДУ 1-ого порядка. Теорема существования и единственности решения задачи Коши для ДУ 1-ого порядка.
Ур-ния вида: y`=f(x,y) имеет бесконечное число решений. Из множества решений можно выделить одно частное решение с помощью задания начального условия Коши: y(x0)=y0 , (x0, y0)?D (*)
Задача отыскания частного решения ДУ y`=f(x,y)удовл. нач.усл.(*) назыв задачей Коши для этого ур-ния с геометрической точки зрения задача Коши для ДУ y`=f(x,y) означает следующее: требуется из множества интегральных кривых выделить ту, которая проходит через заданную точку M0(x0, y0)?D.
Теорема (о существовании и единственности решения задачи Коши). Дусть ф-ия f(x,y) определена, непрерывна и имеет непрерывные частные производные в области D(df/dy), тогда найдется интервал (x0-δ, x0+δ) на котором существует единственное решение y= φ(x) ДУ y`=f(x,y) удовл. условиям y(x0)=y0.
Если условия теоремы выполнены и имеются 2 решения: y= φ1(x) и y= φ2(x) ур-ния y`=f(x,y) такие, что φ1(x0)= φ2(x0), то существует такой интервал (x0-δ, x0+δ) в каждой точке которого φ1(x)= φ2(x).
Геометрическая интерпретация ДУ 1-ого порядка. Метод изоклин.
Из ур-ния y`=f(x,y) следует что угловой коэффициент y` касательной к интегральной кривой в каждой точке (x,y)?D равен значению ф-ии f(x,y) в этой точке.
Таким образом, в каждой точке (x,y)?D можно указать направление касательной к интегральной кривой проходящей через точку (x,y).
Если через каждую точку кривой провести отрезок с коэфф. k=f(x,y) получится поле направлений области D.
Вывод. С геометрической точки зрения ДУ y`=f(x,y) опред. в обл. D плоскости XY поле направлений а решению этого ур-ния соотв. Кривая направлений к косательной к которой в каждой ее точке совпадает с направлением поля в этой точке. Эта задача решается графически и приближенно методом изоклин.
Изоклиной ДУ y`=f(x,y) называется кривая в каждой точке которой поле направлений имеет один и тот же наклон, т.е. семейство изоклин ДУ y`=f(x,y) определяется равенством: f(x,y) = k =tgα, где k-параметр, α-угол наклона поля направлений оси X.
Придавая параметру k близкое численное значение можно получить сеть изоклин с помощью которых приближенно строятся интегральные кривые ДУ y`=f(x,y).
Однородные ДУ 1-ого порядка
Функция f(x,y) называется однородной функцией n–го измерения, если при любом t выполняется условие:  .
.
Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.
Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.
P(x,y)dx=-Q(x,y)dy; 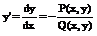 . Однородное уравнение всегда можно привести к виду
. Однородное уравнение всегда можно привести к виду 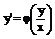 и с помощью замены y/x=t однородное уравнение всегда приводится к уравнению с разделяющимися переменными (y/x=t; y=xt; y’=t+xt’).
и с помощью замены y/x=t однородное уравнение всегда приводится к уравнению с разделяющимися переменными (y/x=t; y=xt; y’=t+xt’).
Такие уравнения с помощью подстановки y = ux и y' = u'x + u, dy=udx+xdy, где u – новая переменная сводятся к уравнениям с разделяющимися переменными u и х.
Пример. Найти общее решение (общий интеграл) дифференциального уравнения y`=2xy/(x2-y2). Проверим, является ли данное уравнение однородным:
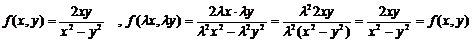 т.е. является. Введем замену:
т.е. является. Введем замену: 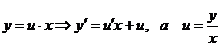 . Подставим в исходное уравнение:
. Подставим в исходное уравнение: 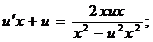
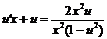
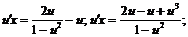
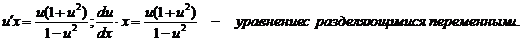
Разделим переменные и проинтегрируем полученное уравнение: 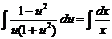 . Найдем интеграл левой части уравнения:
. Найдем интеграл левой части уравнения:

 . Найдем интеграл правой части уравнения:
. Найдем интеграл правой части уравнения:  . Приравняем найденные результаты:
. Приравняем найденные результаты:  . Используем свойства логарифмов и потенцируем равенство:
. Используем свойства логарифмов и потенцируем равенство: 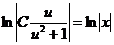 ,
, 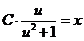 . Подставим вместо
. Подставим вместо 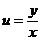 получим
получим 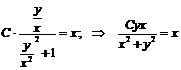 .Общее решение данного дифференциального уравнения имеет вид:
.Общее решение данного дифференциального уравнения имеет вид:  , где С – произвольная постоянная.
, где С – произвольная постоянная.
7.Линейные ДУ 1-ого порядка (метод подстановки Бернулли, метод вариации произвольной постоянной Лагранжа).
ЛДУ - уравнения вида y’+P(x)y=f(x) (21)– первого порядка относительно у и у’. Где P(x) и f(x) заданные ф-ции, линейн относ неизв ф-ции и ее произв-й. Если f(x)=0, то ур-ние линейн однородн.
Для решения ЛДУ применяем замену(подстановка Бернулли): y=UV, тогда y’=U’V+UV’
U’V+UV’+P(x)UV=f(x)
V(U’+P(x)U)+UV’=f(x) (23)
Далее приравняем U’+P(x)U=0 – ур с раздел. переменными, его общ решен:
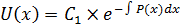 , подстав U(x) в 23:
, подстав U(x) в 23: 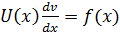 ;(поделим обе части на U(x) и проинтегрир):
;(поделим обе части на U(x) и проинтегрир):  ;
; 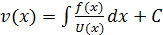 ;подставл найден знач v(x) и u(x) в выр
;подставл найден знач v(x) и u(x) в выр
y(x)=U(x)V(x): y(x)= U(x)(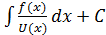 );
);
По методу вариац произв постоян неодн ду (21) ищется в виде:  --реш. неоднор лду в котор C=C(x)-диференц ф-ция. подставив в 21 получим:
--реш. неоднор лду в котор C=C(x)-диференц ф-ция. подставив в 21 получим:
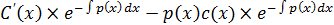 +p(x)
+p(x)  =f(x)
=f(x)
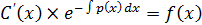 =>
=> 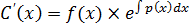
 ; ф-ция с(х) найдена подст в ф-лу 25 оконч получ общ реш ду 21:
; ф-ция с(х) найдена подст в ф-лу 25 оконч получ общ реш ду 21:
y= 
Уравнение Бернулли
урав вида y’+P(x)y=Q(x)  yn,n
yn,n  (26)
(26)
при n=0, оно превр в линейн ду, при n=1 в ур с раздел перемен.
y’+ 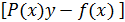 y=0 –ур с разд перем
y=0 –ур с разд перем
рассм случ когда 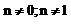 ур Берн сведется к лин диф ур, для этого обе части рав-ва 26 раздел все эл-ты на yn ; y
ур Берн сведется к лин диф ур, для этого обе части рав-ва 26 раздел все эл-ты на yn ; y  0; y=0 – явл решен ур Берн при n=0; yn
0; y=0 – явл решен ур Берн при n=0; yn  y’+P(x) y1-n=f(x) (27). Введем замену перемен: y1-n=z, z=z(x), z’=(1-n)y; y-n
y’+P(x) y1-n=f(x) (27). Введем замену перемен: y1-n=z, z=z(x), z’=(1-n)y; y-n  y’=
y’=  ; Ур 27 примет вид:
; Ур 27 примет вид:
 ; 28 явл лин ду относ задан ф-ции z(x) его реш мож быть получ метод подстан Берн или вариац произв постоян.
; 28 явл лин ду относ задан ф-ции z(x) его реш мож быть получ метод подстан Берн или вариац произв постоян.
Теорема.
Уравнение Р(х,у)dх + Q(x,y)dy=0 с непрерывной диф. функцией Р(х,у) и Q(x,y) является уравнением в полном дифференциале тогда и только тогда, когда выполняется условие: ðP/ðy=ðQ/ðx.
Доказательство.Необходимось:
пусть левая часть ур. Р(х,у)dх + Q(x,y)dy=0 есть полный дифференциал неявной ф-ииu(x,y)
Р(х,у)dх + Q(x,y)dy= 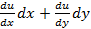
P(x,y)= 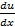 Q(x,y)=
Q(x,y)= 
Продифференцируем 1-е соотношение P(x,y)= 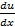 по у, а 2-е Q(x,y)=
по у, а 2-е Q(x,y)= 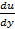 по х.
по х.
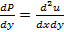 и
и 
В силу равенства получаем: ðP/ðy=ðQ/ðx
Достаточность:
при выполнении усл. 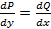 и Р(х,у)dх + Q(x,y)dy=0 есть полный дифференциал некоторой ф-ииu(x,y).
и Р(х,у)dх + Q(x,y)dy=0 есть полный дифференциал некоторой ф-ииu(x,y).
Интегрируя по х из P(x,y)= 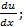 Q(x,y)=
Q(x,y)= 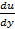 : u(x,y)=
: u(x,y)= 
Подберем ф-ю  чтобы выполнялось 2-е соотношение. Для этого продифференцируем равенство по у и результат приравняем
чтобы выполнялось 2-е соотношение. Для этого продифференцируем равенство по у и результат приравняем 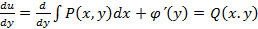
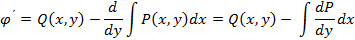
Необходимо показать что первая часть равенства не зависит от х.
Интегрируем рав-во и получаем:

U(x,y)=C общее решение уравнения Р(х,у)dх + Q(x,y)dy=0
10.Дифференциальные уравнения высших порядков. Теорема о существовании и единственности решения. Задача Коши. Приемы понижения порядка (на примерах ДУ 2-ого порядка).
F(x,y, y´…… 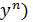 =0 – наз. диф. ур. n-ого порядка. Будем предполагать, что оно разрешается относительно n-ой произ.
=0 – наз. диф. ур. n-ого порядка. Будем предполагать, что оно разрешается относительно n-ой произ.
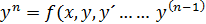 )
)
Теорема Коши.
Если ф-я 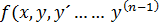 и её частная производная от аргумента y,y´,
и её частная производная от аргумента y,y´,  определена и непрерывна в области R, содерж. точку(
определена и непрерывна в области R, содерж. точку( )то в некоторой окрестности точки х0 существует ед. решение ур.
)то в некоторой окрестности точки х0 существует ед. решение ур. 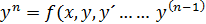 )удавле. усл. y(x0)=y0; y´(x0)=y
)удавле. усл. y(x0)=y0; y´(x0)=y 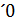 ; …
; … 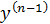 (x0)=
(x0)= 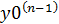 )
)
Это условие есть условие Коши.
Задача отыскания решения ур. 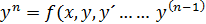 ) удовл. этим усл. наз. задачей Коши для ур.
) удовл. этим усл. наз. задачей Коши для ур. 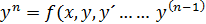 )
)
В зад. Коши для диф. ур. 2-го порядка 
В некоторых частных случаях д.у. высших порядков можно решать методом понижения порядка.
1. у´´=f(x) т.к. у´´=(у´)´, то интегр. левую и правую часть
у´= 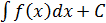
y= 
С1 и С2 – производные константы
2. у´´=f(x, y´), у´=z=z(x), y´´=z´, z´=f(x.y)
z=  z(x)=
z(x)= 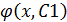
y´= 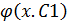
y= 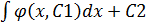 -общее решение
-общее решение
3. y´´=f(y,y´) не содержащие явно независ. переменных х. Вводится новая ф-яz(y) и тогда у´=z;y´´= 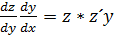
Подставив в исх. ур. полученное ур. z*z´y=f(y,z) в котором играет роль независ. перемен. у. Решив его, найдём z= 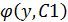 Подставим
Подставим  равнение с разделяющимися переменными
равнение с разделяющимися переменными
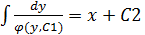 - общее решение диф. ур.
- общее решение диф. ур.
Определение.
Ур.вида у´´+ру´+qy=0, p,q- наз. линейн. однород. диф. ур. с постоянными коэффициентами. Будем иск.решение ур. у´´+ру´+qy=0 в соот. с методом Эйлера у= 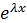
y´= 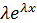
y´´= 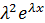
yи y´, y´´ подст. в ур. у´´+ру´+qy=0

 –характеристическое ур.
–характеристическое ур.
1,Пусть корни 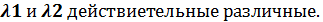
у1= 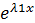
у2= 
Т.к. определитель Вронского 

=  =
= 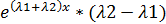
Решение - 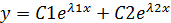
2) 
у1= 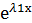 – частное решение уравнения у´´+ру´+qy=0
– частное решение уравнения у´´+ру´+qy=0
Покажем, что в этом случае у2=х 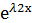 также явл. решением ур. у´´+ру´+qy=0
также явл. решением ур. у´´+ру´+qy=0
Т.к. у2= 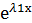 +х
+х 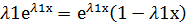
у2= 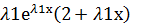
Общее решение ур. 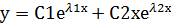
Задачи, приводящие к дифференциальным уравнениям (ДУ). Основные сведения о ДУ (обыкновенные ДУ, ОДУ n-ого порядка, решение ДУ на интервале).
ДУ – ур-ния содержащие неизвестные функции или вектор функции под знаком производной или дифференциала.
1. dx/dt = -kx - уравнение радиоактивного распада, где k-постоянная распада, x- кол-во неразложившегося вещ-ва в момент времени t, dx/dt – скорость распада,которая пропорциональна кол-ву распада.
2. m*(d2r/dt2) = F(t,r,dr/dt) - ур-ние движения точки, массы m под влиянием силы F, зависящей от времени, положения точки радиус вектора и ее скорости.
3. ð2u/ ðx2 + ð2u/ ðy2+ ð2u/ ðz2 = 4πρ(x,y,z) - ур-ние Пуассона, которому удовлетворяет потенциал и (x,y,z) электростатического поля, ρ-плотность зарядов.
ДУ – ур-ние относительно неизвестной функции и ее производных различных порядков. Порядком ДУ называется порядок старшей производной входящей в это уровнение.
ДУ называется обыкновенным, если искомая функция зависит от одной переменной. (пример 1,2)Если искомая функция зависит от нескольких переменных, то ДУ называются ур-ниями с частными производными (пример 3).
Обыкновенные ДУ(ОДУ) n-ого порядка наз. ур-ния вида:F(x,y,y`,y``,…yn)=0, (1)
Где, x-независимая переменная, y=y(x) –зависимая от x-искомая ф-ия переменной x, y`,y``,…yn -производная, F() –заданная ф-ия своих аргументом,может не содержать несколько своих элементов,но должна зависить от yn.
Если ур-ние (1) разрешимо относительно производной n-ого порядка, то можно представить: yn = f(x, y,y`,y``,…yn-1). (2)
Ф-ия y=φ(x) определенная и непрерывная дифференцируемая n раз на (a,b) назыв. Решением ур-ния (1) в этом интервале если она обращает указанное ур-ние в тождество: F(x, φ(x), φ`(x),… φn(x)) =0, для всех х принадлеж. интервалу (a,b).



 .
.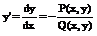 . Однородное уравнение всегда можно привести к виду
. Однородное уравнение всегда можно привести к виду 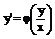 и с помощью замены y/x=t однородное уравнение всегда приводится к уравнению с разделяющимися переменными (y/x=t; y=xt; y’=t+xt’).
и с помощью замены y/x=t однородное уравнение всегда приводится к уравнению с разделяющимися переменными (y/x=t; y=xt; y’=t+xt’).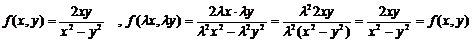 т.е. является. Введем замену:
т.е. является. Введем замену: 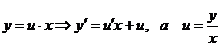 . Подставим в исходное уравнение:
. Подставим в исходное уравнение: 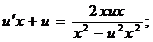
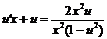
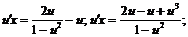
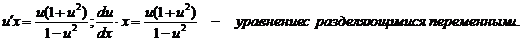
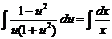 . Найдем интеграл левой части уравнения:
. Найдем интеграл левой части уравнения:
 . Найдем интеграл правой части уравнения:
. Найдем интеграл правой части уравнения:  . Приравняем найденные результаты:
. Приравняем найденные результаты:  . Используем свойства логарифмов и потенцируем равенство:
. Используем свойства логарифмов и потенцируем равенство: 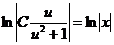 ,
, 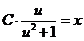 . Подставим вместо
. Подставим вместо 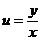 получим
получим 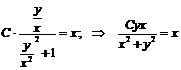 .Общее решение данного дифференциального уравнения имеет вид:
.Общее решение данного дифференциального уравнения имеет вид:  , где С – произвольная постоянная.
, где С – произвольная постоянная.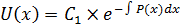 , подстав U(x) в 23:
, подстав U(x) в 23: 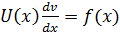 ;(поделим обе части на U(x) и проинтегрир):
;(поделим обе части на U(x) и проинтегрир):  ;
; 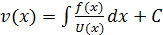 ;подставл найден знач v(x) и u(x) в выр
;подставл найден знач v(x) и u(x) в выр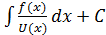 );
); --реш. неоднор лду в котор C=C(x)-диференц ф-ция. подставив в 21 получим:
--реш. неоднор лду в котор C=C(x)-диференц ф-ция. подставив в 21 получим: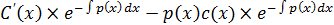 +p(x)
+p(x)  =f(x)
=f(x)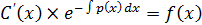 =>
=> 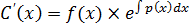
 ; ф-ция с(х) найдена подст в ф-лу 25 оконч получ общ реш ду 21:
; ф-ция с(х) найдена подст в ф-лу 25 оконч получ общ реш ду 21:
 yn,n
yn,n  (26)
(26)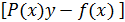 y=0 –ур с разд перем
y=0 –ур с разд перем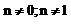 ур Берн сведется к лин диф ур, для этого обе части рав-ва 26 раздел все эл-ты на yn ; y
ур Берн сведется к лин диф ур, для этого обе части рав-ва 26 раздел все эл-ты на yn ; y  0; y=0 – явл решен ур Берн при n=0; yn
0; y=0 – явл решен ур Берн при n=0; yn 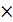 y’+P(x) y1-n=f(x) (27). Введем замену перемен: y1-n=z, z=z(x), z’=(1-n)y; y-n
y’+P(x) y1-n=f(x) (27). Введем замену перемен: y1-n=z, z=z(x), z’=(1-n)y; y-n  ; Ур 27 примет вид:
; Ур 27 примет вид: ; 28 явл лин ду относ задан ф-ции z(x) его реш мож быть получ метод подстан Берн или вариац произв постоян.
; 28 явл лин ду относ задан ф-ции z(x) его реш мож быть получ метод подстан Берн или вариац произв постоян.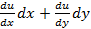
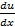 Q(x,y)=
Q(x,y)= 
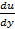 по х.
по х.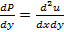 и
и 
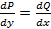 и Р(х,у)dх + Q(x,y)dy=0 есть полный дифференциал некоторой ф-ииu(x,y).
и Р(х,у)dх + Q(x,y)dy=0 есть полный дифференциал некоторой ф-ииu(x,y).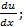 Q(x,y)=
Q(x,y)= 
 чтобы выполнялось 2-е соотношение. Для этого продифференцируем равенство по у и результат приравняем
чтобы выполнялось 2-е соотношение. Для этого продифференцируем равенство по у и результат приравняем 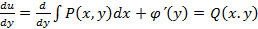
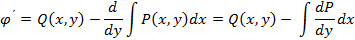

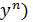 =0 – наз. диф. ур. n-ого порядка. Будем предполагать, что оно разрешается относительно n-ой произ.
=0 – наз. диф. ур. n-ого порядка. Будем предполагать, что оно разрешается относительно n-ой произ.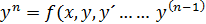 )
)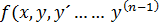 и её частная производная от аргумента y,y´,
и её частная производная от аргумента y,y´,  определена и непрерывна в области R, содерж. точку(
определена и непрерывна в области R, содерж. точку( )то в некоторой окрестности точки х0 существует ед. решение ур.
)то в некоторой окрестности точки х0 существует ед. решение ур. 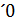 ; …
; … 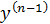 (x0)=
(x0)= 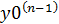 )
)
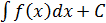

 z(x)=
z(x)= 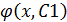
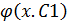
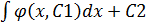 -общее решение
-общее решение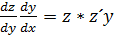
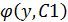 Подставим
Подставим  равнение с разделяющимися переменными
равнение с разделяющимися переменными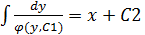 - общее решение диф. ур.
- общее решение диф. ур.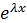
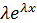
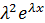

 –характеристическое ур.
–характеристическое ур.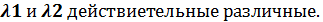
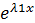



 =
= 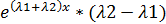
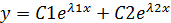

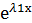 – частное решение уравнения у´´+ру´+qy=0
– частное решение уравнения у´´+ру´+qy=0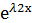 также явл. решением ур. у´´+ру´+qy=0
также явл. решением ур. у´´+ру´+qy=0