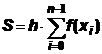, ,
| (6.1)
|
где f (x) - подынтегральная функция, непрерывная на [ a,b ];
a,b - нижний и верхний пределы интегрирования.
Геометрически вычисление определенного интеграла интерпретируется как вычисление площади, ограниченной осью OX и графиком f (x) на промежутке [ a,b ] изменения х (рис.6.1).
К численному вычислению интеграла (численному интегрированию) обращаются в случаях, когда невозможно аналитически записать первообразную интеграла
 через элементарные функции или если такая запись имеет очень сложный вид.
через элементарные функции или если такая запись имеет очень сложный вид.
| 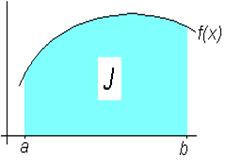 Рис.6.1, Геометрическая
интерпретация определенного
интеграла Рис.6.1, Геометрическая
интерпретация определенного
интеграла
|
Суть большинства методов численного интегрирования состоит в замене подынтегральной функции f (x) аппроксимирующей функцией  , для которой можно легко записать первоообразную в элементарных функциях, т.е.
, для которой можно легко записать первоообразную в элементарных функциях, т.е.
 ,
,
где S - приближенное значение интеграла (6.1);
R - погрешность численного вычисления интеграла J.
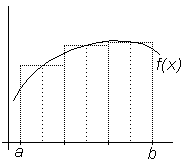
При численном интегрировании независимо от выбранного метода необходимо вычислять приближенное значение S интеграла (1) и оценивать погрешность R. В большинстве методов промежуток интегрирования [ a,b ] разбивается на некоторое число N интервалов, на каждом из которых подынтегральная функция f (x) аппроксимируется и вычисляется частичный интеграл, а конечный результат S есть сумма всех частичных интегралов (рис.6.2).
 Рис.6.2. Геометрическая сущность
численного интегрирования
Рис.6.2. Геометрическая сущность
численного интегрирования
|  Рис.6.3. Зависимость погрешности от
числа разбиений
Рис.6.3. Зависимость погрешности от
числа разбиений
|
Используемые на практике методы численного интегрирования можно сгруппировать в зависимости от способа аппроксимации подынтегральной функции.
1-я группа: методы Ньютона-Котеса. Они основаны на полиномиальной аппроксимации. Методы этой группы отличаются друг от друга степенью используемого полинома, от которой зависит количество узлов, в которых необходимо вычислять значения подынтегральной функции f (x). Алгоритмы этих методов просты и легко поддаются программной реализации.
2-я группа: сплайновые методы. Эти методы различаются типами выбранных сплайнов. Такие методы имеет смысл использовать в задачах, где алгоритмы сплайновой аппроксимации применяются на многих этапах обработки данных.
3-я группа: методы Гаусса-Кристоффеля. Это методы наивысшей алгебраической точности. Они используют не равноотстоящие узлы, расположенные по алгоритму, обеспечивающему минимальную погрешность интегрирования. Алгоритмы этой группы методов требуют большей оперативной памяти ЭВМ, чем алгоритмы 1-ой группы.
4-я группа: методы Монте-Карло. В них используется вероятностный, случайный выбор узлов аппроксимации.
5-я группа: это специальные методы, специализированные под данный вид подынтегральной функции. Они характеризуются высокой точностью, но и большой сложностью алгоритмов и программной реализации.
При увеличении числа N, т.е. при уменьшении длины интервала разбиения, погрешность аппроксимации R будет уменьшаться, но при этом будет возрастать погрешность суммирования Rs частичных интегралов. Начиная с некоторого N o, эта погрешность становится преобладающей, и тогда суммарная погрешность  = R+Rs численного интегрирования будет возрастать (рис.6.3.). Поэтому не следует считать, что неограниченное увеличение N будет давать все более точный результат.
= R+Rs численного интегрирования будет возрастать (рис.6.3.). Поэтому не следует считать, что неограниченное увеличение N будет давать все более точный результат.
Методы прямоугольников
Данные методы относятся к простейшим из класса методов Ньютона-Котеса. В них подынтегральная функция f (x) на каждом интервале разбиения заменяется полиномом нулевой степени, т.е. константой. Такая замена является неоднозначной, т.к. константу можно выбрать равной значению f (x) в любой точке данного интервала разбиения.
В любом случае значение частичного интеграла определяется как произведение длины интервала разбиения на выбранную константу, т.е. как площадь прямоугольника. В зависимости от способа выбора аппроксимирующей константы различают методы левых, средних или правых прямоугольников (рис.6.4).
Рис.6.4. Геометрическая интерпретация методов прямоугольников
Введем следующие обозначения: точку a на оси OX обозначим через x 0, точку b - через x n, а точки разбиения промежутка [ a,b ] - через x 1, x 2,..., x n-1. Предполагается, что длина интервала разбиения постоянна на всем [ a,b ]. Обозначим ее через h:
 ; x i = x i-1 + h, i =1,2,..., N.
; x i = x i-1 + h, i =1,2,..., N.
Тогда в методе левых прямоугольников площадь каждого i -го прямоугольника
| S i = h f (x i), i = 0,1,2,..., n -1,
| (6.2)
|
а для всего промежутка [ a,b ]: 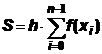



 ,
,
 через элементарные функции или если такая запись имеет очень сложный вид.
через элементарные функции или если такая запись имеет очень сложный вид.
 Рис.6.1, Геометрическая
интерпретация определенного
интеграла
Рис.6.1, Геометрическая
интерпретация определенного
интеграла
 , для которой можно легко записать первоообразную в элементарных функциях, т.е.
, для которой можно легко записать первоообразную в элементарных функциях, т.е. ,
, Рис.6.2. Геометрическая сущность
численного интегрирования
Рис.6.2. Геометрическая сущность
численного интегрирования
 Рис.6.3. Зависимость погрешности от
числа разбиений
Рис.6.3. Зависимость погрешности от
числа разбиений
 = R+Rs численного интегрирования будет возрастать (рис.6.3.). Поэтому не следует считать, что неограниченное увеличение N будет давать все более точный результат.
= R+Rs численного интегрирования будет возрастать (рис.6.3.). Поэтому не следует считать, что неограниченное увеличение N будет давать все более точный результат. Левые
Левые
 Средние
Средние
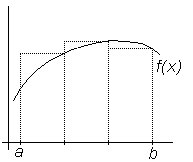 Правые
Правые
 ; x i = x i-1 + h, i =1,2,..., N.
; x i = x i-1 + h, i =1,2,..., N.