1) Масса и статические моменты тела.
Пусть тело занимает объем 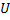 и его объемная плотность в точке
и его объемная плотность в точке 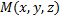 задана функцией
задана функцией  . Тогда масса тела
. Тогда масса тела 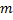 вычисляется с помощью тройного интеграла:
вычисляется с помощью тройного интеграла:
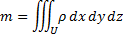
Статические моменты тела относительно координатных плоскостей  ,
,  ,
,  :
:
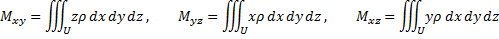
Координаты центра тяжести тела вычисляются по формулам:
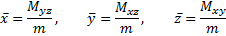
2) Моменты инерции тела.
Моменты инерции тела относительно координатных плоскостей 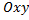 ,
, 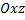 ,
, 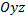 :
:

Моменты инерции тела относительно координатных осей  ,
, 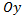 ,
, 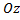 :
:
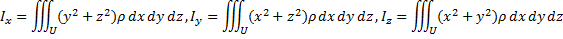
Моментом инерции тела относительно начала координат называется интеграл:
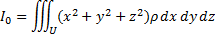
3) Тензор инерции.
Матрица инерции или тензор инерции тела:

4) Гравитационный потенциал и сила тяготения.
Ньютоновым потенциалом тела в точке  называется интеграл:
называется интеграл:

где 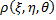 – плотность тела.
– плотность тела.
Интегрирование выполняется по всему объему тела. Зная потенциал, можно вычислить силу притяжения материальной точки массы 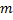 и заданного распределенного тела с плотностью
и заданного распределенного тела с плотностью 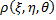 по формуле:
по формуле:
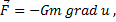
где 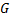 – гравитационная постоянная.
– гравитационная постоянная. 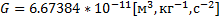 .
.
Криволинейные интегралы.
Криволинейные интегралы 1 и 2 рода, их вычисление и приложения. Формула Остроградского-Гаусса, Грина, Стокса
Криволинейные интегралы 1–го рода.
Определение.
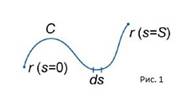
Пусть кривая 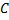 описывается векторной ф.
описывается векторной ф. 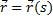 , причём
, причём 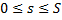 , где переменная
, где переменная 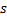 – длина дуги кривой (Рис.1).
– длина дуги кривой (Рис.1).
Если на кривой 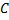 определена скалярная функция
определена скалярная функция 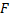 , то интеграл
, то интеграл 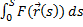 называется криволинейным интегралом первого рода от скалярной ф.
называется криволинейным интегралом первого рода от скалярной ф. 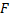 вдоль кривой
вдоль кривой 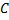 и обозначается:
и обозначается:
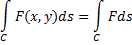
Криволинейный интеграл 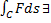 , если ф.
, если ф.  непрерывна на кривой
непрерывна на кривой  .
.
Свойства криволинейного интеграла первого рода:
1) Интеграл не зависит от ориентации кривой;
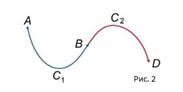
2) Пусть кривая 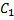 начинается в т.
начинается в т. 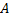 и заканчивается в т.
и заканчивается в т. 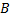 , а кривая
, а кривая 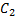 начинается в т.
начинается в т. 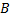 и заканчивается в т.
и заканчивается в т.  (Рис. 2). Тогда их объединением будет кривая
(Рис. 2). Тогда их объединением будет кривая 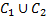 , которая проходит от
, которая проходит от 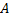 к
к 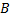 вдоль кривой
вдоль кривой 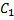 и затем от
и затем от 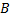 к
к  вдоль кривой
вдоль кривой 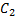 . Тогда справедливо соотношение:
. Тогда справедливо соотношение:
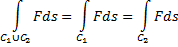
3) Если гладкая кривая 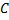 задана параметрически соотношением
задана параметрически соотношением 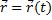 , причём
, причём  и скалярная ф.
и скалярная ф. 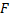 непрерывна на кривой
непрерывна на кривой 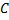 , то:
, то:
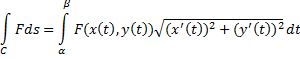
4) Если гладкая кривая 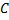 в плоскости
в плоскости  определена ур.
определена ур. 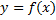 , причём
, причём  , то:
, то:

5) Если гладкая кривая 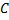 в плоскости
в плоскости  определена ур.
определена ур. 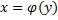 , причём
, причём 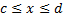 , то:
, то:

6) В полярных координатах интеграл 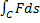 выражается формулой:
выражается формулой:
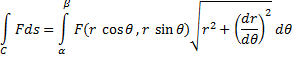
где 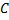 задана в полярных координатах ф.
задана в полярных координатах ф.  , причём
, причём  .
.
 Криволинейные интегралы 2–го рода.
Криволинейные интегралы 2–го рода.
Определение.
Пусть кривая 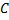 описывается векторной ф.
описывается векторной ф. 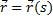 , причём
, причём 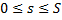 , где переменная
, где переменная 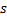 – длина дуги кривой. Тогда производная векторной ф.:
– длина дуги кривой. Тогда производная векторной ф.: 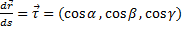 представляет собой единичный вектор, направленный вдоль касательной к данной кривой (Рис 1.)
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (Рис 1.)
В приведенной выше формуле  ,
, 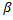 и
и  – углы между касательной и положительными направлениями осей
– углы между касательной и положительными направлениями осей  ,
,  и
и  , соответственно.
, соответственно.
Введем векторную функцию 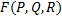 , определенную на кривой
, определенную на кривой 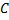 , так, чтобы для скалярной функции:
, так, чтобы для скалярной функции: 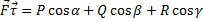 существовал криволинейный интеграл:
существовал криволинейный интеграл: 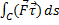 . Такой интеграл называется криволинейным интегралом второго рода от векторной функции
. Такой интеграл называется криволинейным интегралом второго рода от векторной функции 
вдоль кривой C и обозначается как: 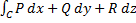 . Таким образом:
. Таким образом:
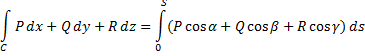
в векторной форме:

где  .
.
Свойства криволинейного интеграла второго рода:
1) Пусть 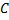 обозначает кривую с началом в точке
обозначает кривую с началом в точке 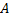 и конечной точкой
и конечной точкой 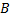 . Обозначим через
. Обозначим через 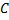
кривую противоположного направления от 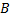 к
к 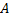 . Тогда:
. Тогда:
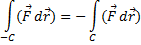
2) Если 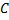 объединение кривых
объединение кривых 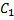 и
и 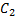 , то:
, то:
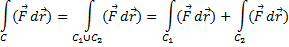
3) Если кривая 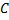 задана параметрически в виде:
задана параметрически в виде: 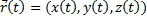 ,
,  , то:
, то:




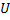 и его объемная плотность в точке
и его объемная плотность в точке 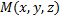 задана функцией
задана функцией  . Тогда масса тела
. Тогда масса тела 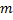 вычисляется с помощью тройного интеграла:
вычисляется с помощью тройного интеграла: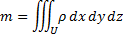
 ,
, 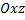 ,
, 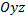 :
: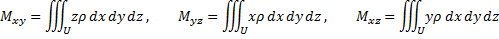
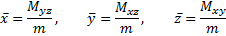
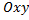 ,
, 
 ,
, 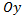 ,
, 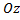 :
: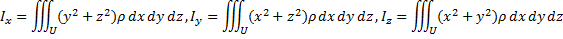
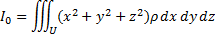

 называется интеграл:
называется интеграл:
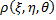 – плотность тела.
– плотность тела.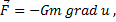
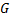 – гравитационная постоянная.
– гравитационная постоянная. 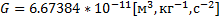 .
.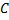 описывается векторной ф.
описывается векторной ф. 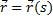 , причём
, причём 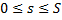 , где переменная
, где переменная 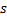 – длина дуги кривой (Рис.1).
– длина дуги кривой (Рис.1).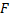 , то интеграл
, то интеграл 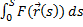 называется криволинейным интегралом первого рода от скалярной ф.
называется криволинейным интегралом первого рода от скалярной ф. 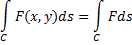
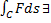 , если ф.
, если ф. 

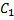 начинается в т.
начинается в т. 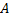 и заканчивается в т.
и заканчивается в т. 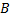 , а кривая
, а кривая 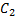 начинается в т.
начинается в т.  (Рис. 2). Тогда их объединением будет кривая
(Рис. 2). Тогда их объединением будет кривая 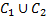 , которая проходит от
, которая проходит от 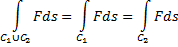
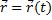 , причём
, причём  и скалярная ф.
и скалярная ф. 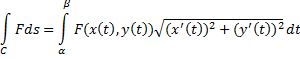
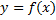 , причём
, причём  , то:
, то:
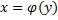 , причём
, причём 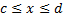 , то:
, то:
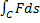 выражается формулой:
выражается формулой: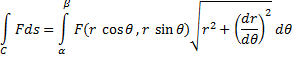
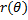 , причём
, причём  .
. Криволинейные интегралы 2–го рода.
Криволинейные интегралы 2–го рода.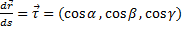 представляет собой единичный вектор, направленный вдоль касательной к данной кривой (Рис 1.)
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (Рис 1.) ,
, 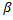 и
и  – углы между касательной и положительными направлениями осей
– углы между касательной и положительными направлениями осей  и
и  , соответственно.
, соответственно.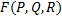 , определенную на кривой
, определенную на кривой 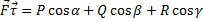 существовал криволинейный интеграл:
существовал криволинейный интеграл: 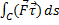 . Такой интеграл называется криволинейным интегралом второго рода от векторной функции
. Такой интеграл называется криволинейным интегралом второго рода от векторной функции 
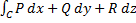 . Таким образом:
. Таким образом: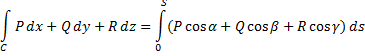

 .
.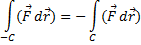
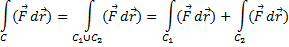
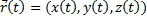 ,
, 



