

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
Топ:
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
■ Декартова прямоугольная система координат. Эта система координат определяется заданием трех взаимно перпендикулярных осей (пересекающихся в одной точке О – начале координат) и единицы масштаба. Оси обычно обозначают Ox, Oy, Oz. Имеет место взаимно однозначное соответствие между точками пространства и тройками чисел x, y, z – координатами точек.

Замечание. Различают правые и левые системы декартовых координат.
■ Расстояние d между двумя точками пространства  и
и  (т.е. длина отрезка АВ) вычисляется по формуле
(т.е. длина отрезка АВ) вычисляется по формуле
 .
.
В частности, расстояние от точки  до начала координат равно
до начала координат равно  .
.
Пример 1. Расстояние между точками A (-3, 1, 5) и B (-2, 0, 4) равно  , а длина отрезка ОА равна
, а длина отрезка ОА равна  .
.
■ Деление отрезка в данном отношении. Пусть даны точки  и
и  . Координаты точки D(x, y, z), делящей отрезок АВ в отношении AD: DB = λ, определяются по формулам
. Координаты точки D(x, y, z), делящей отрезок АВ в отношении AD: DB = λ, определяются по формулам
 ,
,  ,
,  .
.
Координаты середины отрезка (т.е. точки С(x, y, z), делящей отрезок АВ в отношении AС: СB = λ = 1) находятся по формулам
 ,
,  ,
,  .
.
Пример 2. Найти точку D(x, y, z), делящую отрезок АВ в отношении AD: DB = 1,5, если даны координаты точек A (-2, 1, 4) и B (3, 6, -1).
Решение. Находим  ,
, 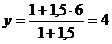 ,
,  .
.
Ответ: D (1, 4, 1).
Векторная алгебра
Векторы
■ Понятие вектора. Различают скалярные величины (такие, как масса, температура, плотность) и векторные величины (сила, скорость, ускорение и т.п.). Скалярные величины охарактеризованы одним числом, выражающим отношение этой величины к единице измерения. Для векторной величины одного числа недостаточно: они обладают еще и направленностью. Для выражения таких величин служат геометрические векторы.
Геометрическим вектором называется направленный отрезок. Векторы обозначаются либо  (точка А – начало вектора, точка В – конец вектора), либо
(точка А – начало вектора, точка В – конец вектора), либо  . Длина отрезка АВ называется модулем вектора
. Длина отрезка АВ называется модулем вектора  и обозначается
и обозначается  (или
(или  ).
).
|
|
Нулевым вектором называется вектор, у которого начало и конец совпадают. Коллинеарными векторами называются векторы, лежащие на одной прямой или на параллельных прямых. Векторы называются равными, если они коллинеарны, имеют одинаковые модули и одинаковые направления.
В геометрии не различают равных векторов, получающихся друг из друга параллельным переносом. В этом смысле векторы называют свободными.
■ Произведение вектора на число. Произведением вектора  на действительное число
на действительное число  называется вектор
называется вектор  , удовлетворяющий трем условиям: 1) модуль вектора
, удовлетворяющий трем условиям: 1) модуль вектора  равен
равен  ; 2) вектор
; 2) вектор  коллинеарен вектору
коллинеарен вектору  ; 3)
; 3)  и
и  направлены одинаково, если
направлены одинаково, если  и противоположно, если
и противоположно, если  (если
(если  , то
, то  , т.е. представляет собой нулевой вектор).
, т.е. представляет собой нулевой вектор).
Вектор  или
или  называется противоположным вектором по отношению к вектору
называется противоположным вектором по отношению к вектору  .
.
■ Сумма векторов. Суммой векторов  и
и  называется вектор
называется вектор  , получаемый либо по правилу параллелограмма (рис. 24, а), либо по правилу треугольника (рис. 24, б). При этом подразумевается, что векторы
, получаемый либо по правилу параллелограмма (рис. 24, а), либо по правилу треугольника (рис. 24, б). При этом подразумевается, что векторы  и
и  предварительно параллельным переносом должны занять положение, показанное на рисунках.
предварительно параллельным переносом должны занять положение, показанное на рисунках.

Рис. 24.
Сумму произвольного числа векторов  можно построить по следующему правилу: приложим вектор
можно построить по следующему правилу: приложим вектор  к концу вектора
к концу вектора  , вектор
, вектор  – к концу вектора
– к концу вектора  и т.д.; тогда сумма n векторов будет представлять собой вектор, идущий из начала вектора
и т.д.; тогда сумма n векторов будет представлять собой вектор, идущий из начала вектора  в конец вектора
в конец вектора  (" правило многоугольника " или " правило замыкающей ").
(" правило многоугольника " или " правило замыкающей ").
Операция сложения векторов обладает свойствами коммутативности  и ассоциативности
и ассоциативности  . Кроме того, для любого вектора
. Кроме того, для любого вектора  ,
, 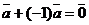 , также
, также 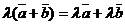 и
и  .
.
■  Разность векторов. Разностью векторов
Разность векторов. Разностью векторов  и
и  называется такой вектор
называется такой вектор  , для которого
, для которого  (см. рис. 25, где векторы
(см. рис. 25, где векторы  и
и  приведены к общему началу).
приведены к общему началу).
Можно рассматривать разность векторов  и
и  как сумму вектора
как сумму вектора  и вектора
и вектора  , противоположного вектору
, противоположного вектору  :
:  .
.
|
|
■ Проекция вектора на ось. Углом 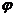 между осью l (направленной прямой) и вектором
между осью l (направленной прямой) и вектором  называется угол кратчайшего поворота оси до совмещения ее направления с направлением вектора (аналогично определяется угол между двумя векторами).
называется угол кратчайшего поворота оси до совмещения ее направления с направлением вектора (аналогично определяется угол между двумя векторами).
Проекция вектора  на ось находится по формуле
на ось находится по формуле

(в случае тупого угла 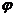 между вектором и осью проекция оказывается отрицательной).
между вектором и осью проекция оказывается отрицательной).
■ Разложение вектора по базису. Координаты вектора. Обозначим через  ,
,  ,
,  единичные векторы (или орты) осей декартовой прямоугольной системы координат Oxyz. Любой вектор
единичные векторы (или орты) осей декартовой прямоугольной системы координат Oxyz. Любой вектор  пространства единственным образом представляется в виде такой линейной комбинации векторов
пространства единственным образом представляется в виде такой линейной комбинации векторов  ,
,  ,
,  :
:
 . (*)
. (*)
Наряду с (*) используется и такая запись:
 .
.
Тройку векторов  ,
,  ,
,  называют координатным базисом пространства, а представление (*) – разложением вектора
называют координатным базисом пространства, а представление (*) – разложением вектора  по базису.
по базису.
Числа X, Y, Z – коэффициенты этого разложения – называются координатами вектора  ; они определяются вектором
; они определяются вектором  однозначно, а именно, они представляют собой проекции вектора на оси координат.
однозначно, а именно, они представляют собой проекции вектора на оси координат.
Замечание. Разложение векторов можно производить не только по ортогональному базису  ,
,  ,
,  , но и по любым трем некомпланарным (т.е. не лежащим в одной плоскости) векторам (если вектор лежит на плоскости, то в качестве базиса можно взять любую пару неколлинеарных векторов).
, но и по любым трем некомпланарным (т.е. не лежащим в одной плоскости) векторам (если вектор лежит на плоскости, то в качестве базиса можно взять любую пару неколлинеарных векторов).
■ Определение координат вектора по координатам его начала и конца. Если даны начало вектора  и его конец
и его конец  , то имеем
, то имеем
 или
или
 .
.
В частном случае, когда начало вектора 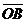 находится в начале координат, имеем
находится в начале координат, имеем  , т.е. в этом случае координаты вектора совпадают с координатами конца вектора (отметим, что вектор
, т.е. в этом случае координаты вектора совпадают с координатами конца вектора (отметим, что вектор 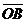 называют радиусом-вектором точки В).
называют радиусом-вектором точки В).
Модуль вектора  (как и длина отрезка АВ) находится по формуле
(как и длина отрезка АВ) находится по формуле
 .
.
В частности, модуль вектора 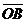 с началом в точке О равен
с началом в точке О равен 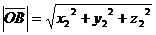 .
.
Пример 1. Пусть начало вектора расположено в точке A (-3, 1, 5), а конец – в точке B (-2, 0, 4). Тогда вектор  или же
или же  , а модуль этого вектора
, а модуль этого вектора  ; радиус-вектор точки В равен
; радиус-вектор точки В равен  , а
, а  .
.
■ Координаты суммы векторов равны суммам одноименных координат слагаемых: если  ,
,  , то
, то  .
.
Аналогично  ; кроме того, координаты вектора
; кроме того, координаты вектора  равны произведениям координат вектора
равны произведениям координат вектора  на число
на число  :
:
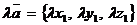 .
.
Пример 2. Найти координаты вектора  , если
, если  ,
,  .
.
Решение. Находим  ,
,  , поэтому
, поэтому
 .
.
Скалярное произведение
■ Определение. Скалярным произведением векторов  и
и  называется число (которое мы будем обозначать
называется число (которое мы будем обозначать  ), равное произведению модулей этих векторов на косинус угла между ними:
), равное произведению модулей этих векторов на косинус угла между ними:
|
|
 . (1)
. (1)
Можно использовать проекции векторов: скалярное произведение векторов  равно произведению
равно произведению  на проекцию вектора
на проекцию вектора  на ось вектора
на ось вектора  или произведению
или произведению  на проекцию вектора
на проекцию вектора  на ось вектора
на ось вектора  :
:
 .
.
Если  и
и  – ненулевые векторы, то при остром угле
– ненулевые векторы, то при остром угле 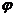 между ними скалярное произведение положительно, а при тупом угле – отрицательно.
между ними скалярное произведение положительно, а при тупом угле – отрицательно.
Скалярное произведение векторов называется произведением потому, что оно обладает алгебраическими свойствами произведения чисел:
 ;
;  ;
;
 .
.
Эти свойства дают возможность перемножать векторные многочлены по обычным правилам алгебры. Отличие же от произведения чисел состоит, в частности, в том, что бессмысленно говорить о скалярном произведении трех (и более) векторов.
■ Физический смысл скалярного произведения. Допустим, что вектор  изображает силу, точка приложения которой перемещается из начала в конец вектора
изображает силу, точка приложения которой перемещается из начала в конец вектора  . Тогда работа этой силы равна
. Тогда работа этой силы равна 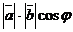 (где
(где 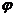 – угол между направлениями силы и перемещения), т.е. работа равна скалярному произведению векторов
– угол между направлениями силы и перемещения), т.е. работа равна скалярному произведению векторов  и
и  .
.
■ Скалярный квадрат вектора. Рассмотрим скалярное произведение  . Оно называется скалярным квадратом вектора
. Оно называется скалярным квадратом вектора  и обозначается
и обозначается  . Имеем
. Имеем
 . (2)
. (2)
Таким образом, скалярный квадрат вектора – неотрицательное число (равное квадрату модуля вектора). В частности, для ортов осей декартовой системы координат имеем  (а
(а  ).
).
■ Выражение скалярного произведения через координаты сомножителей. Если в декартовой прямоугольной системе координат заданы векторы  и
и  , то
, то
 . (3)
. (3)
■ Угол между двумя векторами  и
и  можно найти из соотношения
можно найти из соотношения
 . (4)
. (4)
■ Необходимое и достаточное условие перпендикулярности двух векторов
 (5)
(5)
или, в координатах,
 . (6)
. (6)
 Необходимое и достаточное условие коллинеарности векторов
Необходимое и достаточное условие коллинеарности векторов  и
и  состоит в пропорциональности их координат (т.к.
состоит в пропорциональности их координат (т.к.  ):
):

(если какая-нибудь из координат вектора  равна нулю, то и соответствующая координата вектора
равна нулю, то и соответствующая координата вектора  равна нулю).
равна нулю).
Например, векторы  и
и  коллинеарны, так как выполняется условие
коллинеарны, так как выполняется условие  .
.
|
|
■ Нахождение проекции одного вектора на направление другого. Проекция вектора  на направление вектора
на направление вектора  находится по формуле
находится по формуле  , а проекция
, а проекция  на направление
на направление  – по формуле
– по формуле 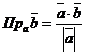 .
.
■ Направляющие косинусы вектора. Обозначим через  углы, образованные вектором
углы, образованные вектором  с осями координат Ox, Oy, Oz соответственно. Тогда числа
с осями координат Ox, Oy, Oz соответственно. Тогда числа  ,
,  ,
,  называются направляющими косинусами вектора
называются направляющими косинусами вектора  . Очевидно,
. Очевидно,
 ,
,  ,
,  ;
;
отсюда ясно, что координатами произвольного единичного вектора  служат его направляющие косинусы:
служат его направляющие косинусы:
 .
.
Направляющие косинусы связаны соотношением
 .
.
■ Проекция вектора на ось. Пусть заданы ось l, имеющая орт (единичный направляющий вектор)  , и некоторый вектор
, и некоторый вектор  . Если
. Если  ,
, 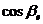 ,
,  – направляющие косинусы орта
– направляющие косинусы орта  , то проекцию вектора
, то проекцию вектора  на ось l можно найти по формуле
на ось l можно найти по формуле
 (см. также стр. ___).
(см. также стр. ___).
Пример 1. Найти скалярное произведение векторов  и
и  , если длины этих векторов соответственно равны 5 и 4, а угол между ними равен 60º.
, если длины этих векторов соответственно равны 5 и 4, а угол между ними равен 60º.
Решение. По определению скалярного произведения (формула (1))  .
.
Ответ:  .
.
Пример 2. Доказать, что векторы  и
и  перпендикулярны.
перпендикулярны.
Решение. Находим скалярное произведение по формуле (3):  . Равенство скалярного произведения нулю означает, что векторы перпендикулярны.
. Равенство скалярного произведения нулю означает, что векторы перпендикулярны.
Пример 3. Найти угол между векторами  и
и  .
.
Решение. Воспользуемся формулой (4):
 ;
;
отсюда  .
.
Пример 4. В треугольнике ABC с вершинами А (1,0,-1), В (2,-1,-5), С (3,-2,4) найти проекцию стороны АВ на сторону АС.
Решение. Находим векторы:
 ,
,  . Искомая проекция равна
. Искомая проекция равна  (отрицательный знак проекции свидетельствует о том, что
(отрицательный знак проекции свидетельствует о том, что  – тупой).
– тупой).
Пример 5. Найти длины диагоналей параллелограмма, построенного на векторах  и
и  , если угол между векторами равен 60º и
, если угол между векторами равен 60º и  ,
,  .
.
Решение. Одна из диагоналей параллелограмма изображается вектором  , а другая – вектором
, а другая – вектором  .
.
Найдем скалярный квадрат  . (здесь мы воспользовались формулой (2)); аналогично
. (здесь мы воспользовались формулой (2)); аналогично 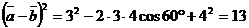 . Из формулы (2) следует, что
. Из формулы (2) следует, что  ; аналогично
; аналогично 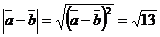 .
.
Ответ: длины диагоналей равны  и
и  .
.
|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!