Аналитическая геометрия в пространстве
Системы координат в пространстве
■ Декартова прямоугольная система координат. Эта система координат определяется заданием трех взаимно перпендикулярных осей (пересекающихся в одной точке О – начале координат) и единицы масштаба. Оси обычно обозначают Ox, Oy, Oz. Имеет место взаимно однозначное соответствие между точками пространства и тройками чисел x, y, z – координатами точек.

Замечание. Различают правые и левые системы декартовых координат.
■ Расстояние d между двумя точками пространства  и
и  (т.е. длина отрезка АВ) вычисляется по формуле
(т.е. длина отрезка АВ) вычисляется по формуле
 .
.
В частности, расстояние от точки  до начала координат равно
до начала координат равно  .
.
Пример 1. Расстояние между точками A (-3, 1, 5) и B (-2, 0, 4) равно  , а длина отрезка ОА равна
, а длина отрезка ОА равна  .
.
■ Деление отрезка в данном отношении. Пусть даны точки  и
и  . Координаты точки D(x, y, z), делящей отрезок АВ в отношении AD: DB = λ, определяются по формулам
. Координаты точки D(x, y, z), делящей отрезок АВ в отношении AD: DB = λ, определяются по формулам
 ,
,  ,
,  .
.
Координаты середины отрезка (т.е. точки С(x, y, z), делящей отрезок АВ в отношении AС: СB = λ = 1) находятся по формулам
 ,
,  ,
,  .
.
Пример 2. Найти точку D(x, y, z), делящую отрезок АВ в отношении AD: DB = 1,5, если даны координаты точек A (-2, 1, 4) и B (3, 6, -1).
Решение. Находим  ,
, 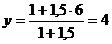 ,
,  .
.
Ответ: D (1, 4, 1).
Векторная алгебра
Векторы
■ Понятие вектора. Различают скалярные величины (такие, как масса, температура, плотность) и векторные величины (сила, скорость, ускорение и т.п.). Скалярные величины охарактеризованы одним числом, выражающим отношение этой величины к единице измерения. Для векторной величины одного числа недостаточно: они обладают еще и направленностью. Для выражения таких величин служат геометрические векторы.
Геометрическим вектором называется направленный отрезок. Векторы обозначаются либо  (точка А – начало вектора, точка В – конец вектора), либо
(точка А – начало вектора, точка В – конец вектора), либо  . Длина отрезка АВ называется модулем вектора
. Длина отрезка АВ называется модулем вектора  и обозначается
и обозначается  (или
(или  ).
).
Нулевым вектором называется вектор, у которого начало и конец совпадают. Коллинеарными векторами называются векторы, лежащие на одной прямой или на параллельных прямых. Векторы называются равными, если они коллинеарны, имеют одинаковые модули и одинаковые направления.
В геометрии не различают равных векторов, получающихся друг из друга параллельным переносом. В этом смысле векторы называют свободными.
■ Произведение вектора на число. Произведением вектора  на действительное число
на действительное число  называется вектор
называется вектор  , удовлетворяющий трем условиям: 1) модуль вектора
, удовлетворяющий трем условиям: 1) модуль вектора  равен
равен  ; 2) вектор
; 2) вектор  коллинеарен вектору
коллинеарен вектору  ; 3)
; 3)  и
и  направлены одинаково, если
направлены одинаково, если  и противоположно, если
и противоположно, если  (если
(если  , то
, то  , т.е. представляет собой нулевой вектор).
, т.е. представляет собой нулевой вектор).
Вектор  или
или  называется противоположным вектором по отношению к вектору
называется противоположным вектором по отношению к вектору  .
.
■ Сумма векторов. Суммой векторов  и
и  называется вектор
называется вектор  , получаемый либо по правилу параллелограмма (рис. 24, а), либо по правилу треугольника (рис. 24, б). При этом подразумевается, что векторы
, получаемый либо по правилу параллелограмма (рис. 24, а), либо по правилу треугольника (рис. 24, б). При этом подразумевается, что векторы  и
и  предварительно параллельным переносом должны занять положение, показанное на рисунках.
предварительно параллельным переносом должны занять положение, показанное на рисунках.

Рис. 24.
Сумму произвольного числа векторов  можно построить по следующему правилу: приложим вектор
можно построить по следующему правилу: приложим вектор  к концу вектора
к концу вектора  , вектор
, вектор  – к концу вектора
– к концу вектора  и т.д.; тогда сумма n векторов будет представлять собой вектор, идущий из начала вектора
и т.д.; тогда сумма n векторов будет представлять собой вектор, идущий из начала вектора  в конец вектора
в конец вектора  (" правило многоугольника " или " правило замыкающей ").
(" правило многоугольника " или " правило замыкающей ").
Операция сложения векторов обладает свойствами коммутативности  и ассоциативности
и ассоциативности  . Кроме того, для любого вектора
. Кроме того, для любого вектора  ,
, 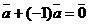 , также
, также 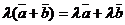 и
и  .
.
■  Разность векторов. Разностью векторов
Разность векторов. Разностью векторов  и
и  называется такой вектор
называется такой вектор  , для которого
, для которого  (см. рис. 25, где векторы
(см. рис. 25, где векторы  и
и  приведены к общему началу).
приведены к общему началу).
Можно рассматривать разность векторов  и
и  как сумму вектора
как сумму вектора  и вектора
и вектора  , противоположного вектору
, противоположного вектору  :
:  .
.
■ Проекция вектора на ось. Углом 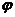 между осью l (направленной прямой) и вектором
между осью l (направленной прямой) и вектором  называется угол кратчайшего поворота оси до совмещения ее направления с направлением вектора (аналогично определяется угол между двумя векторами).
называется угол кратчайшего поворота оси до совмещения ее направления с направлением вектора (аналогично определяется угол между двумя векторами).
Проекция вектора  на ось находится по формуле
на ось находится по формуле

(в случае тупого угла 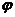 между вектором и осью проекция оказывается отрицательной).
между вектором и осью проекция оказывается отрицательной).
■ Разложение вектора по базису. Координаты вектора. Обозначим через  ,
,  ,
,  единичные векторы (или орты) осей декартовой прямоугольной системы координат Oxyz. Любой вектор
единичные векторы (или орты) осей декартовой прямоугольной системы координат Oxyz. Любой вектор  пространства единственным образом представляется в виде такой линейной комбинации векторов
пространства единственным образом представляется в виде такой линейной комбинации векторов  ,
,  ,
,  :
:
 . (*)
. (*)
Наряду с (*) используется и такая запись:
 .
.
Тройку векторов  ,
,  ,
,  называют координатным базисом пространства, а представление (*) – разложением вектора
называют координатным базисом пространства, а представление (*) – разложением вектора  по базису.
по базису.
Числа X, Y, Z – коэффициенты этого разложения – называются координатами вектора  ; они определяются вектором
; они определяются вектором  однозначно, а именно, они представляют собой проекции вектора на оси координат.
однозначно, а именно, они представляют собой проекции вектора на оси координат.
Замечание. Разложение векторов можно производить не только по ортогональному базису  ,
,  ,
,  , но и по любым трем некомпланарным (т.е. не лежащим в одной плоскости) векторам (если вектор лежит на плоскости, то в качестве базиса можно взять любую пару неколлинеарных векторов).
, но и по любым трем некомпланарным (т.е. не лежащим в одной плоскости) векторам (если вектор лежит на плоскости, то в качестве базиса можно взять любую пару неколлинеарных векторов).
■ Определение координат вектора по координатам его начала и конца. Если даны начало вектора  и его конец
и его конец  , то имеем
, то имеем
 или
или
 .
.
В частном случае, когда начало вектора 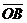 находится в начале координат, имеем
находится в начале координат, имеем  , т.е. в этом случае координаты вектора совпадают с координатами конца вектора (отметим, что вектор
, т.е. в этом случае координаты вектора совпадают с координатами конца вектора (отметим, что вектор 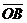 называют радиусом-вектором точки В).
называют радиусом-вектором точки В).
Модуль вектора  (как и длина отрезка АВ) находится по формуле
(как и длина отрезка АВ) находится по формуле
 .
.
В частности, модуль вектора 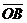 с началом в точке О равен
с началом в точке О равен 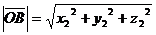 .
.
Пример 1. Пусть начало вектора расположено в точке A (-3, 1, 5), а конец – в точке B (-2, 0, 4). Тогда вектор  или же
или же  , а модуль этого вектора
, а модуль этого вектора  ; радиус-вектор точки В равен
; радиус-вектор точки В равен  , а
, а  .
.
■ Координаты суммы векторов равны суммам одноименных координат слагаемых: если  ,
,  , то
, то  .
.
Аналогично  ; кроме того, координаты вектора
; кроме того, координаты вектора  равны произведениям координат вектора
равны произведениям координат вектора  на число
на число  :
:
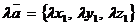 .
.
Пример 2. Найти координаты вектора  , если
, если  ,
,  .
.
Решение. Находим  ,
,  , поэтому
, поэтому
 .
.
Скалярное произведение
■ Определение. Скалярным произведением векторов  и
и  называется число (которое мы будем обозначать
называется число (которое мы будем обозначать  ), равное произведению модулей этих векторов на косинус угла между ними:
), равное произведению модулей этих векторов на косинус угла между ними:
 . (1)
. (1)
Можно использовать проекции векторов: скалярное произведение векторов  равно произведению
равно произведению  на проекцию вектора
на проекцию вектора  на ось вектора
на ось вектора  или произведению
или произведению  на проекцию вектора
на проекцию вектора  на ось вектора
на ось вектора  :
:
 .
.
Если  и
и  – ненулевые векторы, то при остром угле
– ненулевые векторы, то при остром угле 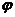 между ними скалярное произведение положительно, а при тупом угле – отрицательно.
между ними скалярное произведение положительно, а при тупом угле – отрицательно.
Скалярное произведение векторов называется произведением потому, что оно обладает алгебраическими свойствами произведения чисел:
 ;
;  ;
;
 .
.
Эти свойства дают возможность перемножать векторные многочлены по обычным правилам алгебры. Отличие же от произведения чисел состоит, в частности, в том, что бессмысленно говорить о скалярном произведении трех (и более) векторов.
■ Физический смысл скалярного произведения. Допустим, что вектор  изображает силу, точка приложения которой перемещается из начала в конец вектора
изображает силу, точка приложения которой перемещается из начала в конец вектора  . Тогда работа этой силы равна
. Тогда работа этой силы равна 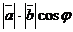 (где
(где 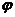 – угол между направлениями силы и перемещения), т.е. работа равна скалярному произведению векторов
– угол между направлениями силы и перемещения), т.е. работа равна скалярному произведению векторов  и
и  .
.
■ Скалярный квадрат вектора. Рассмотрим скалярное произведение  . Оно называется скалярным квадратом вектора
. Оно называется скалярным квадратом вектора  и обозначается
и обозначается  . Имеем
. Имеем
 . (2)
. (2)
Таким образом, скалярный квадрат вектора – неотрицательное число (равное квадрату модуля вектора). В частности, для ортов осей декартовой системы координат имеем  (а
(а  ).
).
■ Выражение скалярного произведения через координаты сомножителей. Если в декартовой прямоугольной системе координат заданы векторы  и
и  , то
, то
 . (3)
. (3)
■ Угол между двумя векторами  и
и  можно найти из соотношения
можно найти из соотношения
 . (4)
. (4)
■ Необходимое и достаточное условие перпендикулярности двух векторов
 (5)
(5)
или, в координатах,
 . (6)
. (6)
 Необходимое и достаточное условие коллинеарности векторов
Необходимое и достаточное условие коллинеарности векторов  и
и  состоит в пропорциональности их координат (т.к.
состоит в пропорциональности их координат (т.к.  ):
):

(если какая-нибудь из координат вектора  равна нулю, то и соответствующая координата вектора
равна нулю, то и соответствующая координата вектора  равна нулю).
равна нулю).
Например, векторы  и
и  коллинеарны, так как выполняется условие
коллинеарны, так как выполняется условие  .
.
■ Нахождение проекции одного вектора на направление другого. Проекция вектора  на направление вектора
на направление вектора  находится по формуле
находится по формуле  , а проекция
, а проекция  на направление
на направление  – по формуле
– по формуле 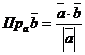 .
.
■ Направляющие косинусы вектора. Обозначим через  углы, образованные вектором
углы, образованные вектором  с осями координат Ox, Oy, Oz соответственно. Тогда числа
с осями координат Ox, Oy, Oz соответственно. Тогда числа  ,
,  ,
,  называются направляющими косинусами вектора
называются направляющими косинусами вектора  . Очевидно,
. Очевидно,
 ,
,  ,
,  ;
;
отсюда ясно, что координатами произвольного единичного вектора  служат его направляющие косинусы:
служат его направляющие косинусы:
 .
.
Направляющие косинусы связаны соотношением
 .
.
■ Проекция вектора на ось. Пусть заданы ось l, имеющая орт (единичный направляющий вектор)  , и некоторый вектор
, и некоторый вектор  . Если
. Если  ,
, 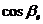 ,
,  – направляющие косинусы орта
– направляющие косинусы орта  , то проекцию вектора
, то проекцию вектора  на ось l можно найти по формуле
на ось l можно найти по формуле
 (см. также стр. ___).
(см. также стр. ___).
Пример 1. Найти скалярное произведение векторов  и
и  , если длины этих векторов соответственно равны 5 и 4, а угол между ними равен 60º.
, если длины этих векторов соответственно равны 5 и 4, а угол между ними равен 60º.
Решение. По определению скалярного произведения (формула (1))  .
.
Ответ:  .
.
Пример 2. Доказать, что векторы  и
и  перпендикулярны.
перпендикулярны.
Решение. Находим скалярное произведение по формуле (3):  . Равенство скалярного произведения нулю означает, что векторы перпендикулярны.
. Равенство скалярного произведения нулю означает, что векторы перпендикулярны.
Пример 3. Найти угол между векторами  и
и  .
.
Решение. Воспользуемся формулой (4):
 ;
;
отсюда  .
.
Пример 4. В треугольнике ABC с вершинами А (1,0,-1), В (2,-1,-5), С (3,-2,4) найти проекцию стороны АВ на сторону АС.
Решение. Находим векторы:
 ,
,  . Искомая проекция равна
. Искомая проекция равна  (отрицательный знак проекции свидетельствует о том, что
(отрицательный знак проекции свидетельствует о том, что  – тупой).
– тупой).
Пример 5. Найти длины диагоналей параллелограмма, построенного на векторах  и
и  , если угол между векторами равен 60º и
, если угол между векторами равен 60º и  ,
,  .
.
Решение. Одна из диагоналей параллелограмма изображается вектором  , а другая – вектором
, а другая – вектором  .
.
Найдем скалярный квадрат  . (здесь мы воспользовались формулой (2)); аналогично
. (здесь мы воспользовались формулой (2)); аналогично 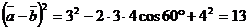 . Из формулы (2) следует, что
. Из формулы (2) следует, что  ; аналогично
; аналогично 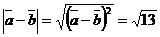 .
.
Ответ: длины диагоналей равны  и
и  .
.
Плоскость в пространстве
■ Векторное уравнение плоскости. Пусть плоскость проходит через точку  и перпендикулярна вектору
и перпендикулярна вектору  . Для произвольной точки плоскости
. Для произвольной точки плоскости  ("текущей точки") векторы
("текущей точки") векторы  и
и 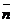 должны быть перпендикулярны. Отсюда получаем векторное уравнение плоскости
должны быть перпендикулярны. Отсюда получаем векторное уравнение плоскости
 .
.
Здесь 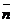 – ненулевой вектор, который называют нормальным вектором плоскости (рис. 28).
– ненулевой вектор, который называют нормальным вектором плоскости (рис. 28).
В координатной форме уравнение плоскости принимает вид
 . (1)
. (1)

Пример 1. Составить уравнение плоскости, проходящей через точку  (-1, 0, 2) и перпендикулярной вектору
(-1, 0, 2) и перпендикулярной вектору  .
.
Решение. Искомое уравнение имеет вид  .
.
■ Общее уравнение плоскости. Уравнению (1) можно придать вид
 . (2)
. (2)
Это уравнение первой степени с тремя переменными, в котором хотя бы один из коэффициентов А, В, С отличен от нуля. Оно называется общим уравнением плоскости.
Любая плоскость определяется уравнением вида (2). Рассмотрим частные случаи общего уравнения плоскости.
1) При  уравнение принимает вид
уравнение принимает вид  ; такая плоскость проходит через начало координат.
; такая плоскость проходит через начало координат.
2) При  ,
,  ,
,  уравнение плоскости
уравнение плоскости  – плоскость параллельна оси Ох (и проходит через нее, если
– плоскость параллельна оси Ох (и проходит через нее, если  ).
).
3) При  ,
,  ,
,  уравнение плоскости
уравнение плоскости  – плоскость параллельна оси Оy (и проходит через нее, если
– плоскость параллельна оси Оy (и проходит через нее, если  ).
).
4) При 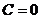 ,
,  ,
,  уравнение плоскости
уравнение плоскости  – плоскость параллельна оси Оz (и проходит через нее, если
– плоскость параллельна оси Оz (и проходит через нее, если  ).
).
5) При  ,
,  ,
,  уравнение плоскости
уравнение плоскости  – плоскость параллельна плоскости хOy (в частности,
– плоскость параллельна плоскости хOy (в частности,  – уравнение плоскости хOy).
– уравнение плоскости хOy).
6) При  ,
, 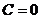 ,
,  уравнение плоскости
уравнение плоскости  – плоскость параллельна плоскости xОz (в частности,
– плоскость параллельна плоскости xОz (в частности,  – уравнение плоскости хOz).
– уравнение плоскости хOz).
7) При  ,
, 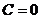 ,
,  уравнение плоскости
уравнение плоскости  – плоскость параллельна плоскости yОz (в частности,
– плоскость параллельна плоскости yОz (в частности,  – уравнение плоскости yOz).
– уравнение плоскости yOz).
Для построения плоскости на чертеже достаточно получить какие-нибудь три точки данной плоскости. Чаще всего находят точки пересечения плоскости с осями координат (если плоскость не параллельна ни одной из осей).
Пример 2. Построить плоскость, заданную уравнением  .
.
Решение. а) положим  ,
,  , тогда
, тогда  ; получаем точку пересечения плоскости с осью Ох: Р (2, 0, 0); б) положим
; получаем точку пересечения плоскости с осью Ох: Р (2, 0, 0); б) положим  ,
,  , тогда
, тогда  ; получаем точку пересечения плоскости с осью Оу: Q (0, 3, 0); в) положим
; получаем точку пересечения плоскости с осью Оу: Q (0, 3, 0); в) положим  ,
,  , тогда
, тогда  ; получаем точку пересечения плоскости с осью Оz: R (0, 0, 6). Для наглядного изображения плоскости остается соединить отрезками прямых три полученные точки Р,Q, R (рис. 29, а).
; получаем точку пересечения плоскости с осью Оz: R (0, 0, 6). Для наглядного изображения плоскости остается соединить отрезками прямых три полученные точки Р,Q, R (рис. 29, а).
Пример 3. Построить плоскость, заданную уравнением  .
.
Решение. а) положим  ,
,  , тогда
, тогда  ; получим точку пересечения плоскости с осью Ох: Р (2, 0, 0); б) положим
; получим точку пересечения плоскости с осью Ох: Р (2, 0, 0); б) положим  ,
,  , тогда
, тогда  ; получим точку пересечения плоскости с осью Оz: R (0, 0, 3). Соединим отрезком прямой точки P и R, после чего нетрудно представить себе, как выглядит данная плоскость (рис. 29, б).
; получим точку пересечения плоскости с осью Оz: R (0, 0, 3). Соединим отрезком прямой точки P и R, после чего нетрудно представить себе, как выглядит данная плоскость (рис. 29, б).

Рис. 29.
■ Уравнение плоскости в отрезках на осях. Если (а, 0, 0), (0, b, 0), (0, 0, с) – точки пересечения плоскости с осями Ох, Оу, Oz соответственно (здесь а, b, с не равны нулю), то уравнению такой плоскости можно придать форму
 . (3)
. (3)
Это "уравнение плоскости в отрезках". Эта форма уравнения плоскости особенно удобна для построения плоскости на чертеже. Если в уравнении (2) коэффициенты и свободный член не равны нулю, можно записать его в виде  , т.е. придать ему форму (3).
, т.е. придать ему форму (3).
■ Нормальное уравнение плоскости. Аналогично тому, как это делалось для уравнения прямой на плоскости (см. п.1.6.), общее уравнение плоскости  можно привести к нормальному виду, деля его на число
можно привести к нормальному виду, деля его на число  , где знак перед корнем берется противоположным знаку свободного члена D.
, где знак перед корнем берется противоположным знаку свободного члена D.
Для нахождения расстояния от данной точки  до данной плоскости
до данной плоскости  надо привести уравнение плоскости к нормальному виду, а затем подставить в левую часть нормального уравнения плоскости координаты
надо привести уравнение плоскости к нормальному виду, а затем подставить в левую часть нормального уравнения плоскости координаты  данной точки М. Тогда искомое расстояние равно абсолютной величине полученного при этом числа h, т.е. равно
данной точки М. Тогда искомое расстояние равно абсолютной величине полученного при этом числа h, т.е. равно
 .
.
Замечание. Если  , т.е. если плоскость не проходит через начало координат, то при h<0 точка М и начало координат лежат по одну сторону от данной плоскости, а при h>0 – по разные стороны (при h=0, очевидно, точка М лежит на плоскости).
, т.е. если плоскость не проходит через начало координат, то при h<0 точка М и начало координат лежат по одну сторону от данной плоскости, а при h>0 – по разные стороны (при h=0, очевидно, точка М лежит на плоскости).
Пример 4. Найти расстояние от точки М (1, 2, 3) до плоскости  .
.
Решение. 1) Приводим уравнение плоскости к нормальному виду, деля его на  (знак плюс взят потому, что
(знак плюс взят потому, что  ):
):  ;
;
2) Подставляя в левую часть этого уравнения 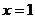 ,
,  ,
,  , получим число
, получим число  . Таким образом, искомое расстояние равно
. Таким образом, искомое расстояние равно  . Тот факт, что
. Тот факт, что  , свидетельствует о том, что точки М и О лежат по разные стороны от заданной плоскости.
, свидетельствует о том, что точки М и О лежат по разные стороны от заданной плоскости.
Пример 5. Найти расстояние между двумя параллельными плоскостями  и
и  .
.
Решение. Возьмем произвольную точку на первой плоскости, например, точку М (0, -1, 0). Искомое расстояние равно, очевидно, расстоянию от точки М до второй плоскости, т.е.  .
.
Ответ:  .
.
■ Угол между двумя плоскостями. Пусть две плоскости заданы общими уравнениями
 ,
,
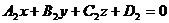 . (4)
. (4)
Угол 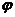 между их нормальными векторами
между их нормальными векторами  и
и  равен (двугранному) углу между данными плоскостями. Поэтому угол между плоскостями можно найти из формулы
равен (двугранному) углу между данными плоскостями. Поэтому угол между плоскостями можно найти из формулы

(см. формулу (4) из п. 2.3.). Это угол 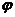 лежит в пределах от 0 до
лежит в пределах от 0 до  ; другой двугранный угол, образованный двумя пересекающимися плоскостями, равен
; другой двугранный угол, образованный двумя пересекающимися плоскостями, равен  .
.
■ Условие перпендикулярности двух плоскостей. Две данные плоскости (4) перпендикулярны тогда и только тогда, когда  , т.е. при выполнении условия
, т.е. при выполнении условия
 или
или 
(см. формулу (5) из п. 2.3.).
Например, плоскости  и
и  перпендикулярны, так как
перпендикулярны, так как  .
.
Две данные плоскости параллельны тогда и только тогда, когда их нормальные векторы  и
и  коллинеарны, т.е. при выполнении условия
коллинеарны, т.е. при выполнении условия
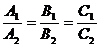 .
.
Здесь, как и в п.2.3, при равенстве нулю какого-нибудь из знаменателей следует считать равным нулю и соответствующий числитель.
Например, плоскости  и
и  параллельны, так как
параллельны, так как 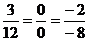 . Заметим дополнительно, что если выполняются равенства
. Заметим дополнительно, что если выполняются равенства  , то это говорит о том, что плоскости совпадают, т.е. уравнения (4) определяют одну и ту же плоскость.
, то это говорит о том, что плоскости совпадают, т.е. уравнения (4) определяют одну и ту же плоскость.
Пример 6. Составить уравнение плоскости, которая проходит через точку М 0(1, -1, 0) и параллельна плоскости  .
.
Решение. Так как у нужной нам плоскости, очевидно, тот же самый нормальный вектор {2, 3, -4}, что и у заданной плоскости, то искомое уравнение должно иметь вид  или
или  – ответ.
– ответ.
Пример 7. Найти угол между плоскостями, заданными уравнениями  и
и  .
.
Решение. Находим косинус угла 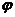 между нормальными векторами
между нормальными векторами 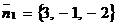 и
и  :
:  ;
;
отсюда  . Это один из двугранных углов, образованных плоскостями; другой угол равен
. Это один из двугранных углов, образованных плоскостями; другой угол равен  .
.
■ Уравнение пучка плоскостей. Все плоскости, проходящие через линию пересечения двух (не параллельных) данных плоскостей (4) ("пучок плоскостей"), представляются уравнением вида
 ,
,
где p и q – произвольные числа, не равные нулю одновременно. Придавая p и q конкретные значения, получаем уравнение той или иной плоскости, проходящей через прямую, по которой пересекаются две данные плоскости. Например, при 
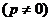 получим уравнение первой плоскости, а при
получим уравнение первой плоскости, а при 
 – уравнение второй плоскости.
– уравнение второй плоскости.
Пример 8. Составить уравнение плоскости, проходящей через линию пересечения двух плоскостей  и
и  и через начало координат.
и через начало координат.
Решение. Искомое уравнение содержится в уравнении пучка плоскостей
 ,
,
где p и q – некоторые числа, причем  (в противном случае это уравнение дало бы плоскость
(в противном случае это уравнение дало бы плоскость  , которая не проходит через начало координат). Поэтому искомое уравнение можно записать в виде
, которая не проходит через начало координат). Поэтому искомое уравнение можно записать в виде
 .
.
Требование, чтобы плоскость проходила через начало координат, приводит к равенству 
|
|
|


 и
и  (т.е. длина отрезка АВ) вычисляется по формуле
(т.е. длина отрезка АВ) вычисляется по формуле .
. .
. , а длина отрезка ОА равна
, а длина отрезка ОА равна  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 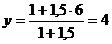 ,
,  .
. (точка А – начало вектора, точка В – конец вектора), либо
(точка А – начало вектора, точка В – конец вектора), либо  . Длина отрезка АВ называется модулем вектора
. Длина отрезка АВ называется модулем вектора  (или
(или  ).
). называется вектор
называется вектор  , удовлетворяющий трем условиям: 1) модуль вектора
, удовлетворяющий трем условиям: 1) модуль вектора  ; 2) вектор
; 2) вектор  и противоположно, если
и противоположно, если  (если
(если  , то
, то  , т.е. представляет собой нулевой вектор).
, т.е. представляет собой нулевой вектор). или
или  называется противоположным вектором по отношению к вектору
называется противоположным вектором по отношению к вектору  называется вектор
называется вектор  , получаемый либо по правилу параллелограмма (рис. 24, а), либо по правилу треугольника (рис. 24, б). При этом подразумевается, что векторы
, получаемый либо по правилу параллелограмма (рис. 24, а), либо по правилу треугольника (рис. 24, б). При этом подразумевается, что векторы 
 можно построить по следующему правилу: приложим вектор
можно построить по следующему правилу: приложим вектор  к концу вектора
к концу вектора  , вектор
, вектор  – к концу вектора
– к концу вектора  (" правило многоугольника " или " правило замыкающей ").
(" правило многоугольника " или " правило замыкающей "). и ассоциативности
и ассоциативности  . Кроме того, для любого вектора
. Кроме того, для любого вектора  ,
, 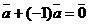 , также
, также 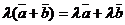 и
и  .
. Разность векторов. Разностью векторов
Разность векторов. Разностью векторов  , для которого
, для которого  (см. рис. 25, где векторы
(см. рис. 25, где векторы  , противоположного вектору
, противоположного вектору  .
.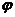 между осью l (направленной прямой) и вектором
между осью l (направленной прямой) и вектором 
 ,
,  ,
,  единичные векторы (или орты) осей декартовой прямоугольной системы координат Oxyz. Любой вектор
единичные векторы (или орты) осей декартовой прямоугольной системы координат Oxyz. Любой вектор  . (*)
. (*) .
. или
или .
.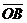 находится в начале координат, имеем
находится в начале координат, имеем  , т.е. в этом случае координаты вектора совпадают с координатами конца вектора (отметим, что вектор
, т.е. в этом случае координаты вектора совпадают с координатами конца вектора (отметим, что вектор  .
.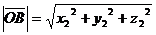 .
. или же
или же  , а модуль этого вектора
, а модуль этого вектора  ; радиус-вектор точки В равен
; радиус-вектор точки В равен  , а
, а  .
. ,
,  , то
, то  .
. ; кроме того, координаты вектора
; кроме того, координаты вектора 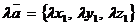 .
. , если
, если  ,
,  .
. ,
,  , поэтому
, поэтому .
. ), равное произведению модулей этих векторов на косинус угла между ними:
), равное произведению модулей этих векторов на косинус угла между ними: . (1)
. (1) на проекцию вектора
на проекцию вектора  .
. ;
;  ;
; .
.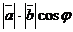 (где
(где  . Оно называется скалярным квадратом вектора
. Оно называется скалярным квадратом вектора  . Имеем
. Имеем . (2)
. (2) (а
(а  ).
). и
и  , то
, то . (3)
. (3) . (4)
. (4) (5)
(5) . (6)
. (6) Необходимое и достаточное условие коллинеарности векторов
Необходимое и достаточное условие коллинеарности векторов  ):
):
 и
и  коллинеарны, так как выполняется условие
коллинеарны, так как выполняется условие  .
. , а проекция
, а проекция 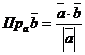 .
. углы, образованные вектором
углы, образованные вектором  ,
,  ,
,  называются направляющими косинусами вектора
называются направляющими косинусами вектора  ,
,  ,
,  ;
; служат его направляющие косинусы:
служат его направляющие косинусы: .
. .
. ,
, 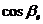 ,
,  – направляющие косинусы орта
– направляющие косинусы орта  (см. также стр. ___).
(см. также стр. ___). .
. .
. и
и  перпендикулярны.
перпендикулярны. . Равенство скалярного произведения нулю означает, что векторы перпендикулярны.
. Равенство скалярного произведения нулю означает, что векторы перпендикулярны. и
и  .
. ;
; .
. ,
,  . Искомая проекция равна
. Искомая проекция равна  (отрицательный знак проекции свидетельствует о том, что
(отрицательный знак проекции свидетельствует о том, что  – тупой).
– тупой). ,
,  .
. .
. . (здесь мы воспользовались формулой (2)); аналогично
. (здесь мы воспользовались формулой (2)); аналогично 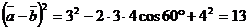 . Из формулы (2) следует, что
. Из формулы (2) следует, что  ; аналогично
; аналогично 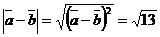 .
. и
и  .
. и перпендикулярна вектору
и перпендикулярна вектору  . Для произвольной точки плоскости
. Для произвольной точки плоскости  ("текущей точки") векторы
("текущей точки") векторы  и
и 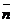 должны быть перпендикулярны. Отсюда получаем векторное уравнение плоскости
должны быть перпендикулярны. Отсюда получаем векторное уравнение плоскости .
. . (1)
. (1)
 (-1, 0, 2) и перпендикулярной вектору
(-1, 0, 2) и перпендикулярной вектору  .
. .
. . (2)
. (2) уравнение принимает вид
уравнение принимает вид  ; такая плоскость проходит через начало координат.
; такая плоскость проходит через начало координат. ,
,  ,
,  уравнение плоскости
уравнение плоскости  – плоскость параллельна оси Ох (и проходит через нее, если
– плоскость параллельна оси Ох (и проходит через нее, если  ,
,  ,
,  – плоскость параллельна оси Оy (и проходит через нее, если
– плоскость параллельна оси Оy (и проходит через нее, если 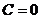 ,
,  уравнение плоскости
уравнение плоскости  – плоскость параллельна оси Оz (и проходит через нее, если
– плоскость параллельна оси Оz (и проходит через нее, если  – плоскость параллельна плоскости хOy (в частности,
– плоскость параллельна плоскости хOy (в частности,  – уравнение плоскости хOy).
– уравнение плоскости хOy). – плоскость параллельна плоскости xОz (в частности,
– плоскость параллельна плоскости xОz (в частности,  – уравнение плоскости хOz).
– уравнение плоскости хOz). – плоскость параллельна плоскости yОz (в частности,
– плоскость параллельна плоскости yОz (в частности,  – уравнение плоскости yOz).
– уравнение плоскости yOz). .
. ; получаем точку пересечения плоскости с осью Ох: Р (2, 0, 0); б) положим
; получаем точку пересечения плоскости с осью Ох: Р (2, 0, 0); б) положим  ; получаем точку пересечения плоскости с осью Оу: Q (0, 3, 0); в) положим
; получаем точку пересечения плоскости с осью Оу: Q (0, 3, 0); в) положим  ; получаем точку пересечения плоскости с осью Оz: R (0, 0, 6). Для наглядного изображения плоскости остается соединить отрезками прямых три полученные точки Р,Q, R (рис. 29, а).
; получаем точку пересечения плоскости с осью Оz: R (0, 0, 6). Для наглядного изображения плоскости остается соединить отрезками прямых три полученные точки Р,Q, R (рис. 29, а). .
. ; получим точку пересечения плоскости с осью Оz: R (0, 0, 3). Соединим отрезком прямой точки P и R, после чего нетрудно представить себе, как выглядит данная плоскость (рис. 29, б).
; получим точку пересечения плоскости с осью Оz: R (0, 0, 3). Соединим отрезком прямой точки P и R, после чего нетрудно представить себе, как выглядит данная плоскость (рис. 29, б).
 . (3)
. (3) , т.е. придать ему форму (3).
, т.е. придать ему форму (3). , где знак перед корнем берется противоположным знаку свободного члена D.
, где знак перед корнем берется противоположным знаку свободного члена D. до данной плоскости
до данной плоскости  данной точки М. Тогда искомое расстояние равно абсолютной величине полученного при этом числа h, т.е. равно
данной точки М. Тогда искомое расстояние равно абсолютной величине полученного при этом числа h, т.е. равно .
. , т.е. если плоскость не проходит через начало координат, то при h<0 точка М и начало координат лежат по одну сторону от данной плоскости, а при h>0 – по разные стороны (при h=0, очевидно, точка М лежит на плоскости).
, т.е. если плоскость не проходит через начало координат, то при h<0 точка М и начало координат лежат по одну сторону от данной плоскости, а при h>0 – по разные стороны (при h=0, очевидно, точка М лежит на плоскости). .
. (знак плюс взят потому, что
(знак плюс взят потому, что  ):
):  ;
;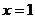 ,
,  ,
,  . Таким образом, искомое расстояние равно
. Таким образом, искомое расстояние равно  . Тот факт, что
. Тот факт, что  , свидетельствует о том, что точки М и О лежат по разные стороны от заданной плоскости.
, свидетельствует о том, что точки М и О лежат по разные стороны от заданной плоскости. и
и  .
. .
. .
. ,
,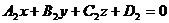 . (4)
. (4) и
и  равен (двугранному) углу между данными плоскостями. Поэтому угол между плоскостями можно найти из формулы
равен (двугранному) углу между данными плоскостями. Поэтому угол между плоскостями можно найти из формулы
 ; другой двугранный угол, образованный двумя пересекающимися плоскостями, равен
; другой двугранный угол, образованный двумя пересекающимися плоскостями, равен  .
. , т.е. при выполнении условия
, т.е. при выполнении условия или
или 
 и
и  перпендикулярны, так как
перпендикулярны, так как  .
. и
и  коллинеарны, т.е. при выполнении условия
коллинеарны, т.е. при выполнении условия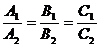 .
. и
и  параллельны, так как
параллельны, так как 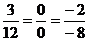 . Заметим дополнительно, что если выполняются равенства
. Заметим дополнительно, что если выполняются равенства  , то это говорит о том, что плоскости совпадают, т.е. уравнения (4) определяют одну и ту же плоскость.
, то это говорит о том, что плоскости совпадают, т.е. уравнения (4) определяют одну и ту же плоскость. .
. или
или  – ответ.
– ответ. и
и  .
.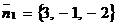 и
и  :
:  ;
; . Это один из двугранных углов, образованных плоскостями; другой угол равен
. Это один из двугранных углов, образованных плоскостями; другой угол равен  .
. ,
,
 получим уравнение первой плоскости, а при
получим уравнение первой плоскости, а при 
 – уравнение второй плоскости.
– уравнение второй плоскости. и
и  и через начало координат.
и через начало координат. ,
, (в противном случае это уравнение дало бы плоскость
(в противном случае это уравнение дало бы плоскость  .
.