При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками. Интервальной называют оценку, которая определяется двумя числами — концами интервала.
Пусть по данным выборки  для оценки параметр известного распределения генеральной совокупности подобрана статистика
для оценки параметр известного распределения генеральной совокупности подобрана статистика  . Заменяя неизвестное значение
. Заменяя неизвестное значение  числом
числом  , мы совершаем ошибку. Тогда случайная величина
, мы совершаем ошибку. Тогда случайная величина  – абсолютное значение ошибки. Если d>0 и |q–
– абсолютное значение ошибки. Если d>0 и |q–  |<d, то чем меньше d, тем оценка точнее. Таким образом, положительное число d характеризует точность оценки. Однако статистические методы не позволяют категорично утверждать, что оценка
|<d, то чем меньше d, тем оценка точнее. Таким образом, положительное число d характеризует точность оценки. Однако статистические методы не позволяют категорично утверждать, что оценка  удовлетворяет неравенству |q–
удовлетворяет неравенству |q–  |<d; можно лишь говорить о вероятности g, скоторой это неравенство осуществляется. Если известен закон распределения случайной величины
|<d; можно лишь говорить о вероятности g, скоторой это неравенство осуществляется. Если известен закон распределения случайной величины  , то эту вероятность можно найти
, то эту вероятность можно найти  . Если для небольших d вероятность g достаточно велика, то число
. Если для небольших d вероятность g достаточно велика, то число  можно считать точной и надежной оценкой неизвестного параметра
можно считать точной и надежной оценкой неизвестного параметра  .
.
Надежностью (доверительной вероятностью) оценки q по  называют вероятность g, с которой осуществляется неравенство |q—
называют вероятность g, с которой осуществляется неравенство |q—  |<d. Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
|<d. Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть  .
.
Заменив неравенство |q –  | < d равносильным ему двойным неравенством – d<q—
| < d равносильным ему двойным неравенством – d<q—  < d, или
< d, или  – d<q <
– d<q <  + d, имеем
+ d, имеем

Это соотношение следует понимать так: вероятность того, что интервал ( – d,
– d,  + d) заключает в себе (покрывает) неизвестный параметр q, равна g.
+ d) заключает в себе (покрывает) неизвестный параметр q, равна g.
Доверительным называют интервал ( – d,
– d,  + d), который покрывает неизвестный параметр с заданной надежностью g.
+ d), который покрывает неизвестный параметр с заданной надежностью g.
2.4. Доверительный интервал для оценки математического ожидания нормально распределенной генеральной совокупности, когда дисперсия s2 генеральной совокупности известна
Рассмотрим случайную величину 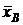 – выборочное среднее:
– выборочное среднее:
 .
.
Так как генеральная совокупность распределена по нормальному закону, 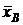 тоже имеет нормальное распределение,
тоже имеет нормальное распределение,  ,
,  . Рассмотрим интервал
. Рассмотрим интервал  , или
, или 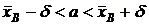 . Ширину
. Ширину 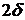 этого интервала определим из условия
этого интервала определим из условия 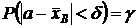 , где g – заданная доверительная вероятность.
, где g – заданная доверительная вероятность.
Можно показать, что в этом случае 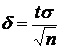 , где число t определяется из таблицы функции Лапласа из условия
, где число t определяется из таблицы функции Лапласа из условия  .
.
Таким образом, получаем
 .
.
Смысл полученного соотношения таков: с надежностью g можно утверждать, что доверительный интервал  покрывает неизвестный параметр а.
покрывает неизвестный параметр а.
Замечание 1. Оценку 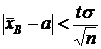 называют классической. Из формулы
называют классической. Из формулы 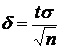 можно сделать следующие выводы:
можно сделать следующие выводы:
1) при возрастании объема выборки п число d убывает и, следовательно, точность оценки увеличивается;
2) увеличение надежности оценки g = 2Ф(t) приводит к увеличению t (Ф (t) – возрастающая функция), следовательно, и к возрастанию d; другими словами, увеличение надежности классической оценки влечет за собой уменьшение ее точности.
Замечание 2. Когда объем выборки  при построении доверительного интервала для a можно пользоваться нормальным распределением, подставляя в формулу для ширины интервала вместо неизвестного значения s число s, определяемое по выборке.
при построении доверительного интервала для a можно пользоваться нормальным распределением, подставляя в формулу для ширины интервала вместо неизвестного значения s число s, определяемое по выборке.
Замечание 4. Оценка истинного значения измеряемой величины. Пусть производится п независимых равноточных измерений некоторой физической величины, истинное значение а которой неизвестно. Будем рассматривать результаты отдельных измерений как случайные величины  . Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии
. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии  2 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в предыдущих параграфах, выполняются, и, следовательно, мы вправе использовать полученные в них формулы. Другими словами, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.
2 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в предыдущих параграфах, выполняются, и, следовательно, мы вправе использовать полученные в них формулы. Другими словами, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.



 для оценки параметр известного распределения генеральной совокупности подобрана статистика
для оценки параметр известного распределения генеральной совокупности подобрана статистика  . Заменяя неизвестное значение
. Заменяя неизвестное значение  числом
числом  , мы совершаем ошибку. Тогда случайная величина
, мы совершаем ошибку. Тогда случайная величина  – абсолютное значение ошибки. Если d>0 и |q–
– абсолютное значение ошибки. Если d>0 и |q–  |<d, то чем меньше d, тем оценка точнее. Таким образом, положительное число d характеризует точность оценки. Однако статистические методы не позволяют категорично утверждать, что оценка
|<d, то чем меньше d, тем оценка точнее. Таким образом, положительное число d характеризует точность оценки. Однако статистические методы не позволяют категорично утверждать, что оценка  . Если для небольших d вероятность g достаточно велика, то число
. Если для небольших d вероятность g достаточно велика, то число  .
.
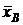 – выборочное среднее:
– выборочное среднее: .
. ,
,  . Рассмотрим интервал
. Рассмотрим интервал  , или
, или 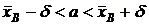 . Ширину
. Ширину 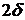 этого интервала определим из условия
этого интервала определим из условия 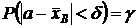 , где g – заданная доверительная вероятность.
, где g – заданная доверительная вероятность.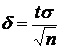 , где число t определяется из таблицы функции Лапласа из условия
, где число t определяется из таблицы функции Лапласа из условия  .
. .
. покрывает неизвестный параметр а.
покрывает неизвестный параметр а.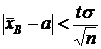 называют классической. Из формулы
называют классической. Из формулы  при построении доверительного интервала для a можно пользоваться нормальным распределением, подставляя в формулу для ширины интервала вместо неизвестного значения s число s, определяемое по выборке.
при построении доверительного интервала для a можно пользоваться нормальным распределением, подставляя в формулу для ширины интервала вместо неизвестного значения s число s, определяемое по выборке. . Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии
. Эти величины независимы (измерения независимы), имеют одно и то же математическое ожидание а (истинное значение измеряемой величины), одинаковые дисперсии  2 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в предыдущих параграфах, выполняются, и, следовательно, мы вправе использовать полученные в них формулы. Другими словами, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.
2 (измерения равноточны) и распределены нормально (такое допущение подтверждается опытом). Таким образом, все предположения, которые были сделаны при выводе доверительных интервалов в предыдущих параграфах, выполняются, и, следовательно, мы вправе использовать полученные в них формулы. Другими словами, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов отдельных измерений при помощи доверительных интервалов.


