 (1.49)
(1.49)
 (1.50)
(1.50)
Передаточные функции по управляющему и возмущающему воздействию, при этом возмущающее воздействие принимается равным нулю. При использовании этих передаточных функций рассматривается переходный процесс при холостом ходе. На основании передаточной функции (1.50) запишем операторное уравнение
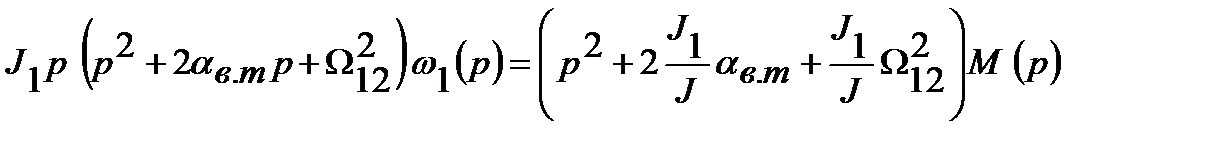

Будем рассматривать переходной процесс при М = const, тогда
 è
è  .
.
Поскольку Мс = 0, то М = Мдин, а это позволяет записать
 ,
,
где eср – среднее ускорение двухмассовой системы.
Теперь получаем дифференциальное уравнение:
 ,
,
решение которого можно записать в виде  ,
,
где w¢ - решение соответствующего однородного уравнения,
w¢¢ - частное решение неоднородного уравнения.
Характеристическое уравнение соответствующего однородного уравнения имеет вид
 Корни этого уравнения:
Корни этого уравнения: 
где 
Wр – резонансная частота двухмассовой системы при наличии диссипативных сил.
Корень p1= 0 (t1® ¥) соответствует установившемуся движению, т. е. частному решению дифференциального уравнения:
 ,è
,è 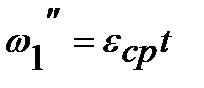
Решение соответствующего однородного уравнения будем искать в виде  , где А и В – постоянные интегрирования.
, где А и В – постоянные интегрирования.
 .
.
Постоянные интегрирования А и В находим из начальных условий (t = 0):
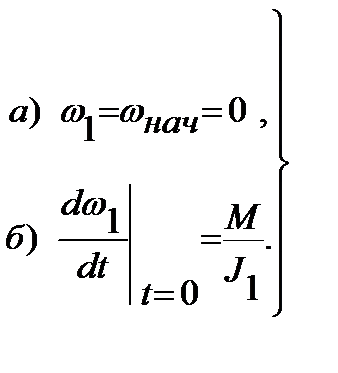 Используем первое условие: 0 =А+В, В = - А
Используем первое условие: 0 =А+В, В = - А
. Находим производную

и определяем ее при t = 0:  .
.  ,
,
что при подстановке в (1.368) дает равенство

из которого определяем 
В результате получаем уравнение угловой скорости первой массы
 , где
, где  .
.
Теперь найдем уравнение для скорости w2 второй массы. На основании передаточной функции (1.49) записываем операторное уравнение
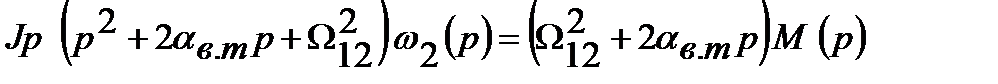 ,
,
которое затем представляем в дифференциальной форме

Полагаем снова М = const, тогда
 .
.
С учетом (1.357) это уравнение принимает вид
 .
.
Решение этого уравнения можно записать:
 ,
,
где постоянные интегрирования C и D находятся из начальных условий (t = 0):
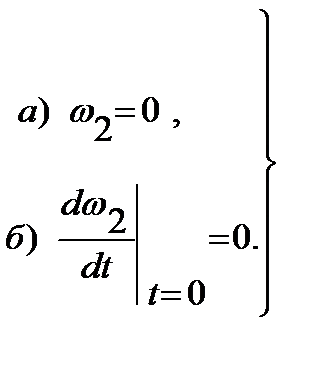 Из первого условия находим D = - C и
Из первого условия находим D = - C и
 .
.
 , откуда
, откуда  .
.  .
.
Из полученных уравнений w1 и w2 видно, что в двухмассовой системе электропривода при постоянном динамическом моменте скорость только в среднем изменяется линейно. На линейно изменяющуюся скорость накладываются колебательные составляющие, которые для обеих скоростей находятся в противофазе. В результате ускорения двигателя в переходном процессе не остается постоянным. При наличии диссипативных сил колебания затухают (рис.1.31). Если диссипативные силы отсутствуют, т. е.  , то
, то
 ,
,  .
.
23. ДИНАМИЧЕСКИЙ КОЭФФИЦИЕНТ ДВУХМАССОВОЙ МОЖДЕЛИ
Неравномерное изменение скорости приводит к возрастанию динамических нагрузок электропривода. Увеличение нагрузок оценивается динамическим коэффициентом
 ,
,
где Му.max и Му.ср – максимальный и средний упругие моменты.
При отсутствии колебаний скорости момент нагрузки передачи равен среднему упругому моменту:  .
.
Вследствие колебаний скорости передаваемый момент становится другим:  .
.



 (1.49)
(1.49) (1.50)
(1.50)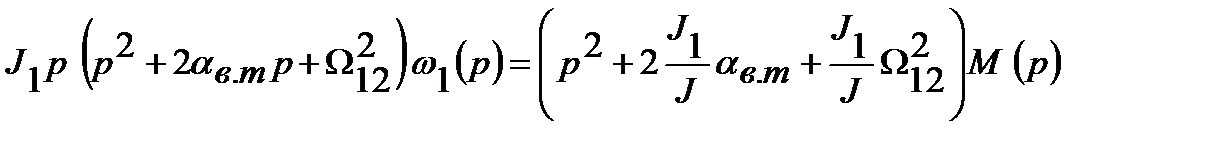

 è
è  .
. ,
, ,
, ,
, Корни этого уравнения:
Корни этого уравнения: 

 ,è
,è 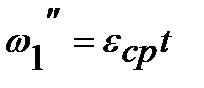
 , где А и В – постоянные интегрирования.
, где А и В – постоянные интегрирования. .
.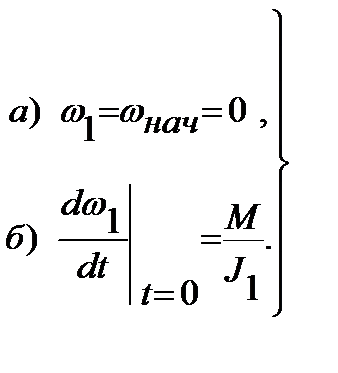 Используем первое условие: 0 =А+В, В = - А
Используем первое условие: 0 =А+В, В = - А
 .
.  ,
,

 , где
, где  .
.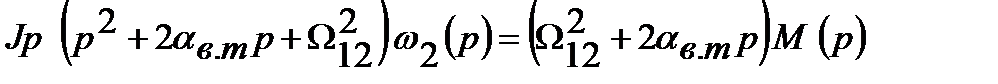 ,
,
 .
. .
. ,
,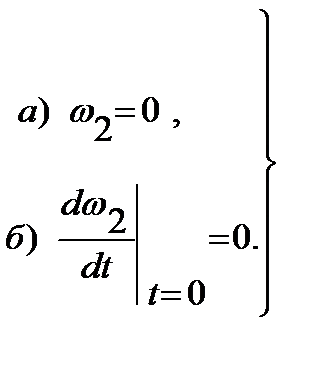 Из первого условия находим D = - C и
Из первого условия находим D = - C и .
. , откуда
, откуда  .
.  .
. , то
, то ,
,  .
. ,
, .
. .
.

