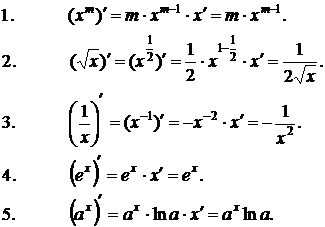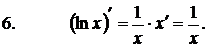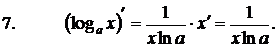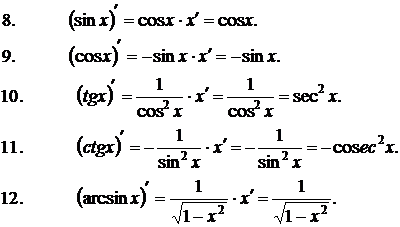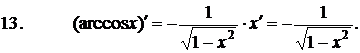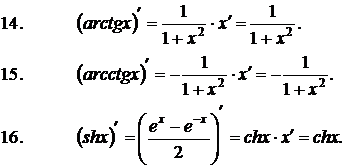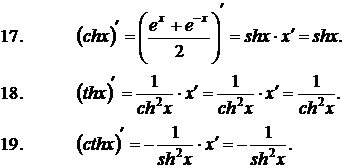Пример 1. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору 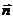 (3, -1).
(3, -1).
Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.
Получаем: 3 – 2 + C = 0, следовательно С = -1.
Итого: искомое уравнение: 3х – у – 1 = 0.
Пример 2. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Применяя уравнение прямой, проходящей через 2 точки, получаем:
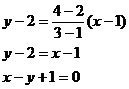
Пример 3. Найти уравнение прямой с направляющим вектором 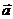 (1, -1) и проходящей через точку А(1, 2).
(1, -1) и проходящей через точку А(1, 2).
Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1×A + (-1)×B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C/A = 0.
при х = 1, у = 2 получаем С/A = -3, т.е. искомое уравнение:
х + у - 3 = 0
Пример 4. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1, 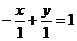 , а = -1, b = 1.
, а = -1, b = 1.
Пример 5. Дано общее уравнение прямой 12х – 5у – 65 = 0. Требуется написать различные типы уравнений этой прямой.
уравнение этой прямой в отрезках: 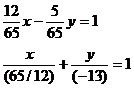
уравнение этой прямой с угловым коэффициентом: (делим на 5)
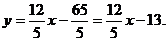
нормальное уравнение прямой:
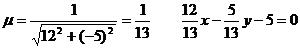 ; cosj = 12/13; sinj = -5/13; p = 5.
; cosj = 12/13; sinj = -5/13; p = 5.
Пример 6. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треугольника, образованного этими отрезками равна 8 см2.
Уравнение прямой имеет вид: 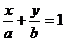 , a = b = 1; ab/2 = 8; a = 4; -4.
, a = b = 1; ab/2 = 8; a = 4; -4.
a = -4 не подходит по условию задачи.
Итого: 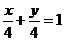 или х + у – 4 = 0.
или х + у – 4 = 0.
Пример 7. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Уравнение прямой имеет вид: 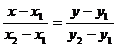 , где х1 = у1 = 0; x2 = -2; y2 = -3.
, где х1 = у1 = 0; x2 = -2; y2 = -3.
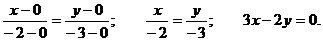
Пример 8. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.
k1 = -3; k2 = 2 tgj= 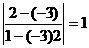 ; j = p/4.
; j = p/4.
Пример 9. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.
Находим: k1 = 3/5, k2 = -5/3, k1k2 = -1, следовательно, прямые перпендикулярны.
Пример 10. Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.
Находим уравнение стороны АВ: 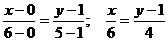 ; 4x = 6y – 6;
; 4x = 6y – 6;
2x – 3y + 3 = 0; 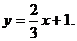
Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.
k= 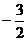 . Тогда y =
. Тогда y = 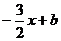 . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению:
. Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 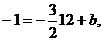 откуда b = 17. Итого:
откуда b = 17. Итого: 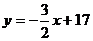 .
.
Ответ: 3x + 2y – 34 = 0.
Раздел 3. Математический анализ
ТЕМА 1. Пределы функций
Для определения пределов последовательностей и функций используются некоторые известные приемы:
1. Если необходимо найти предел
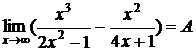 ,
,
можно предварительно привести к общему знаменателю
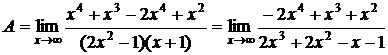 .
.
Поделив на член, имеющий максимальную степень, получим в числителе постоянную величину, а в знаменателе – все члены, стремящиеся к 0,то есть
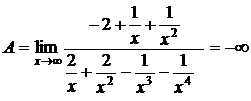 .
.
2. Аналогично, для примера 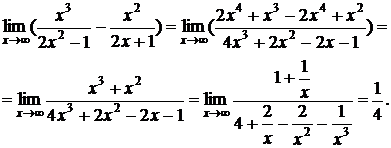
3. 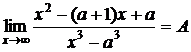 в этом пределе, если подставить x=a, то получится неопределенность, которую можно преодолеть, если разложить разность кубов в знаменателе
в этом пределе, если подставить x=a, то получится неопределенность, которую можно преодолеть, если разложить разность кубов в знаменателе 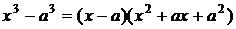 , а числитель в виде:
, а числитель в виде: 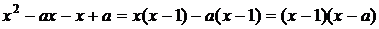 .
.
Тогда 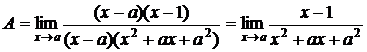 и подставив x=a, получим:
и подставив x=a, получим: 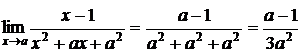 ;
;
4. 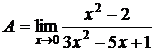 , при подстановке х=0, получим
, при подстановке х=0, получим 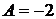 .
.
5. Однако, если необходимо найти предел рациональной функции
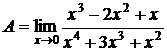 , то при делении на член с минимальной степенью, получим
, то при делении на член с минимальной степенью, получим
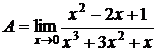 ; и, устремив х к 0, получим:
; и, устремив х к 0, получим: 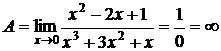
Если в пределах содержатся иррациональные выражения, то приходится вводить новые переменные для получения рационального выражения, или же переводить иррациональности из знаменателя в числитель и наоборот.
6. 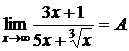 ; Сделаем замену переменной. Заменим
; Сделаем замену переменной. Заменим 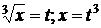 , при
, при 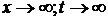 , получим
, получим 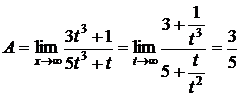 .
.
7. 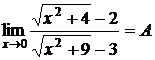 . Если числитель и знаменатель умножить на одно и то же число, то предел не изменится. Умножим числитель на
. Если числитель и знаменатель умножить на одно и то же число, то предел не изменится. Умножим числитель на 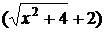 и разделим на это же выражение, чтобы предел не изменился, а знаменатель умножим на
и разделим на это же выражение, чтобы предел не изменился, а знаменатель умножим на 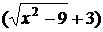 и разделим, на это же выражение. Тогда получим:
и разделим, на это же выражение. Тогда получим:
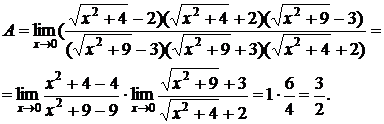
Для определения пределов часто используются замечательные пределы:
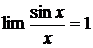 ; (1)
; (1)
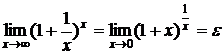 . (2)
. (2)
8. 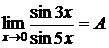 .
.
Для вычисления такого предела сведем его к 1-му замечательному пределу (1). Для этого умножим и разделим числитель на 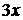 , а знаменатель на
, а знаменатель на 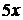 , тогда
, тогда 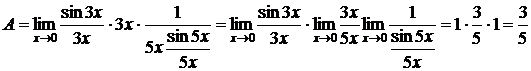 .
.
9. 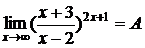 Для вычисления этого предела сведем его ко второму замечательному пределу. С этой целью из рационального выражения в скобках выделим целую часть и представим ее в виде правильной дроби. Так поступают в тех случаях, когда
Для вычисления этого предела сведем его ко второму замечательному пределу. С этой целью из рационального выражения в скобках выделим целую часть и представим ее в виде правильной дроби. Так поступают в тех случаях, когда 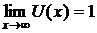 , где
, где 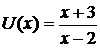 , а
, а 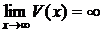 , где
, где 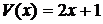 ;
;
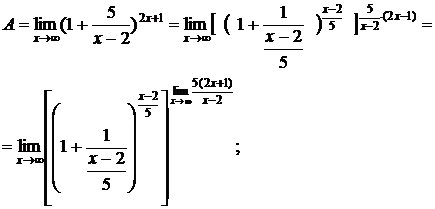
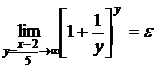 , а
, а 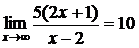 , то окончательно
, то окончательно 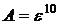 . Здесь использовалась непрерывность композиции непрерывных функций.
. Здесь использовалась непрерывность композиции непрерывных функций.
ТЕМА 2. Производная
Производной от функции 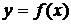 называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
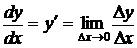 , или
, или 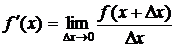 .
.
Геометрически производная представляет собой угловой коэффициент касательной к графику функции 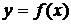 в точке х, то есть
в точке х, то есть 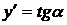 .
.
Производная есть скорость изменения функции в точке х.
Отыскание производной называется дифференцированием функции.
Формулы дифференцирования элементарных функций:
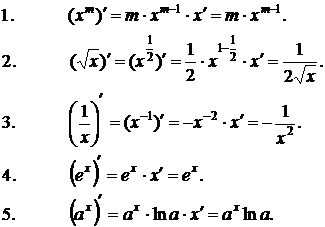
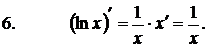
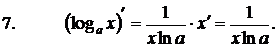
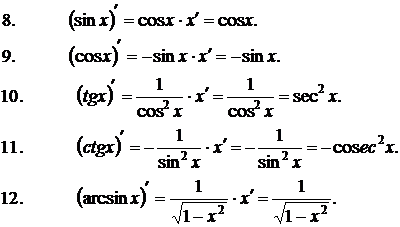
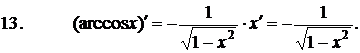
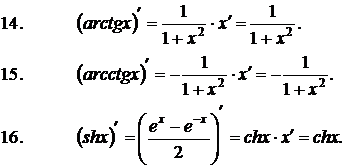



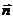 (3, -1).
(3, -1).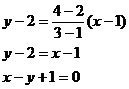
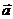 (1, -1) и проходящей через точку А(1, 2).
(1, -1) и проходящей через точку А(1, 2).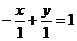 , а = -1, b = 1.
, а = -1, b = 1.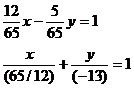
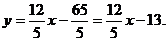
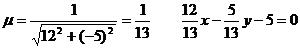 ; cosj = 12/13; sinj = -5/13; p = 5.
; cosj = 12/13; sinj = -5/13; p = 5.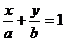 , a = b = 1; ab/2 = 8; a = 4; -4.
, a = b = 1; ab/2 = 8; a = 4; -4.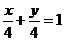 или х + у – 4 = 0.
или х + у – 4 = 0.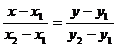 , где х1 = у1 = 0; x2 = -2; y2 = -3.
, где х1 = у1 = 0; x2 = -2; y2 = -3.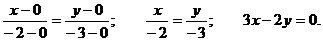
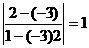 ; j = p/4.
; j = p/4.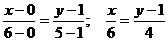 ; 4x = 6y – 6;
; 4x = 6y – 6;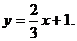
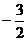 . Тогда y =
. Тогда y = 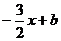 . Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению:
. Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 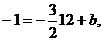 откуда b = 17. Итого:
откуда b = 17. Итого: 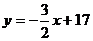 .
.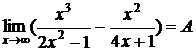 ,
,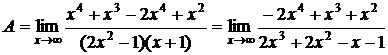 .
.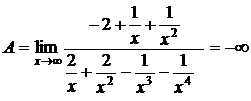 .
.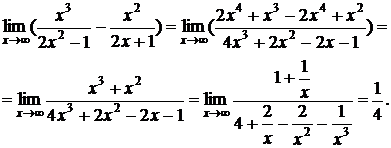
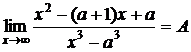 в этом пределе, если подставить x=a, то получится неопределенность, которую можно преодолеть, если разложить разность кубов в знаменателе
в этом пределе, если подставить x=a, то получится неопределенность, которую можно преодолеть, если разложить разность кубов в знаменателе 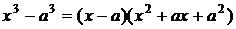 , а числитель в виде:
, а числитель в виде: 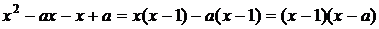 .
.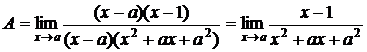 и подставив x=a, получим:
и подставив x=a, получим: 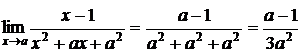 ;
;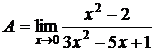 , при подстановке х=0, получим
, при подстановке х=0, получим 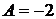 .
.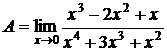 , то при делении на член с минимальной степенью, получим
, то при делении на член с минимальной степенью, получим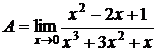 ; и, устремив х к 0, получим:
; и, устремив х к 0, получим: 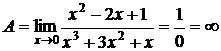
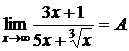 ; Сделаем замену переменной. Заменим
; Сделаем замену переменной. Заменим 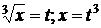 , при
, при 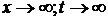 , получим
, получим 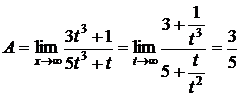 .
.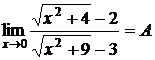 . Если числитель и знаменатель умножить на одно и то же число, то предел не изменится. Умножим числитель на
. Если числитель и знаменатель умножить на одно и то же число, то предел не изменится. Умножим числитель на 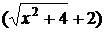 и разделим на это же выражение, чтобы предел не изменился, а знаменатель умножим на
и разделим на это же выражение, чтобы предел не изменился, а знаменатель умножим на 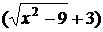 и разделим, на это же выражение. Тогда получим:
и разделим, на это же выражение. Тогда получим: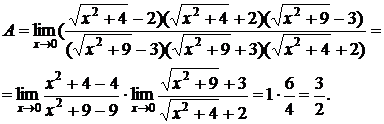
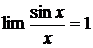 ; (1)
; (1)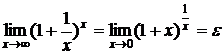 . (2)
. (2)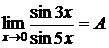 .
.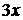 , а знаменатель на
, а знаменатель на 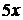 , тогда
, тогда 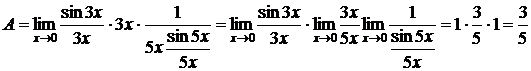 .
.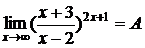 Для вычисления этого предела сведем его ко второму замечательному пределу. С этой целью из рационального выражения в скобках выделим целую часть и представим ее в виде правильной дроби. Так поступают в тех случаях, когда
Для вычисления этого предела сведем его ко второму замечательному пределу. С этой целью из рационального выражения в скобках выделим целую часть и представим ее в виде правильной дроби. Так поступают в тех случаях, когда 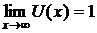 , где
, где 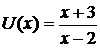 , а
, а 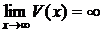 , где
, где 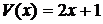 ;
;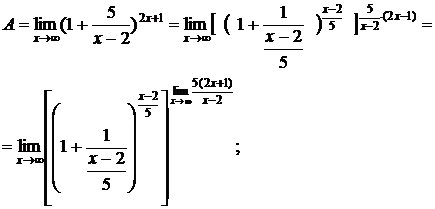
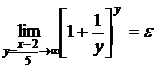 , а
, а 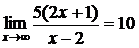 , то окончательно
, то окончательно 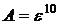 . Здесь использовалась непрерывность композиции непрерывных функций.
. Здесь использовалась непрерывность композиции непрерывных функций.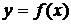 называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю: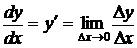 , или
, или 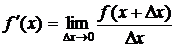 .
.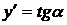 .
.