

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Наибольшее и наименьшее значения функции на отрезке
Для того, чтобы найти  и
и  , нужно найти точки, где
, нужно найти точки, где  , либо не существует, а также
, либо не существует, а также  и
и  . Из найденных значений следует выбрать наименьшее и наибольшее.
. Из найденных значений следует выбрать наименьшее и наибольшее.
Пример 2. Найти наибольшее и наименьшее значение функции  на отрезке
на отрезке  .
.
Решение.
Вычислим производную данной функции и точки, где она равна нулю.
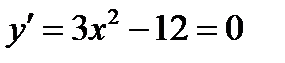 , если
, если  .
.
Обе точки принадлежат рассматриваемому интервалу.
I. Найдем  и
и  и сравним полученные результаты.
и сравним полученные результаты.  откуда
откуда

Интервалы выпуклости, вогнутости графика функции, точки перегиба.
Определение 4. График дифференцируемой функции  называется выпуклым на интервале
называется выпуклым на интервале  , если он расположен ниже любой своей касательной на этом интервале.
, если он расположен ниже любой своей касательной на этом интервале.
Определение 5. График дифференцируемой функции  называется вогнутым на интервале
называется вогнутым на интервале  , если он расположен выше любой своей касательной на этом интервале.
, если он расположен выше любой своей касательной на этом интервале.
Определение 6. Точка графика непрерывной функции, отделяющая ее выпуклую часть от вогнутой, называется точкой перегиба (рис. 7). Здесь точки  и
и  – точки перегиба.
– точки перегиба.

Рис.7
Условие выпуклости, вогнутости графика функции на интервале (а, в).
Пусть функция у =  непрерывна вместе со своими производными
непрерывна вместе со своими производными 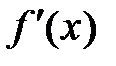 и
и  на
на  .
.
1.Если  , то график функции
, то график функции  будет выпуклым на интервале
будет выпуклым на интервале 
2.Если  , то график функции
, то график функции  будет вогнутым на интервале
будет вогнутым на интервале  .
.
3. Для того, чтобы точка  была точкой перегиба, необходимо, чтобы
была точкой перегиба, необходимо, чтобы  (или не существовала) и достаточно, чтобы
(или не существовала) и достаточно, чтобы  меняла свой знак при переходе через
меняла свой знак при переходе через  .
.
Эти условия регламентируют все действия для выделения интервалов выпуклости, вогнутости и точек перегиба.
Пример 3. Определить интервалы выпуклости, вогнутости графика функции и точки перегиба.
 .
.
Решение: Область существования этой функции, а также производная 1 порядка были найдены в примере 1: 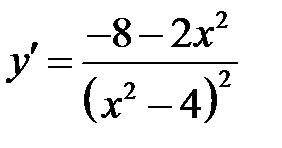 . Найдем производную 2 порядка:
. Найдем производную 2 порядка:  .
.
|
|
2.  , если
, если 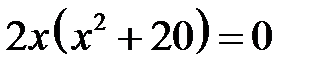 ,
,  . Единственная точка, подозрительная на перегиб, это точка
. Единственная точка, подозрительная на перегиб, это точка  .
.
3.Находим знаки  с учетом интервалов непрерывности
с учетом интервалов непрерывности
и делаем выводы.
1. 
 , следовательно, кривая выпукла
, следовательно, кривая выпукла
2. 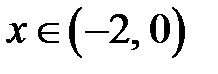
 - кривая вогнута
- кривая вогнута
3  - точка перегиба,
- точка перегиба, 
4. 
 - кривая вогнута
- кривая вогнута
5. 
 - кривая вогнута
- кривая вогнута
График этой функции приведен на рис..6.
Асимптоты функции
Определение 7. Прямая L называется асимптотой кривой  , если расстояние точки М (х, у), принадлежащей кривой от прямой L стремятся к нулю при неограниченном удалении от начала координат.
, если расстояние точки М (х, у), принадлежащей кривой от прямой L стремятся к нулю при неограниченном удалении от начала координат.
Поскольку любая прямая в декартовой системе координат может быть либо параллельна осям координат, либо наклонена под произвольным углом  к оси
к оси  , то и асимптоты могут быть горизонтальными, вертикальными и наклонными (рис.8).
, то и асимптоты могут быть горизонтальными, вертикальными и наклонными (рис.8).

рис. 8.1 рис.8.2 рис 8.3
Вертикальную асимптотуфункция 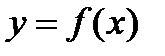 имеет в точках разрыва 2-го рода, где один или оба односторонние предела не существуют, т. е.
имеет в точках разрыва 2-го рода, где один или оба односторонние предела не существуют, т. е.  . Это точки, где знаменатель обращается в нуль или граничные точки области определения функции (рис.8.1).
. Это точки, где знаменатель обращается в нуль или граничные точки области определения функции (рис.8.1).
Уравнение вертикальной асимптоты
х = а (1)
Прямая у = в (рис 8.2), является горизонтальной асимптотой, если выполняются условия:. 
 (2)
(2)
Прямая y= kx+ b является наклонной асимптотой, (рис. 8.3), если существует пределы, позволяющие определить значения коэффициентов «k» и «b» по формулам:
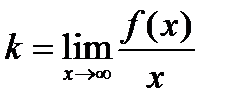
 (3)
(3)
Пример 4. Найти асимптоты следующих функций:
1) 
Решение. Функция имеет одну точку бесконечного разрыва:  , поэтому прямая
, поэтому прямая 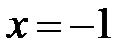 – вертикальная асимптота.
– вертикальная асимптота.
2) 
Решение. Функция имеет одну точку разрыва: 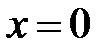 . В ней знаменатель обращается в нуль и
. В ней знаменатель обращается в нуль и 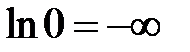 и правосторонний предел равен
и правосторонний предел равен
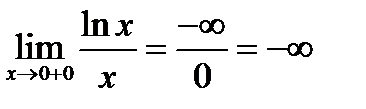
Следовательно, прямая  т.е. ось
т.е. ось  , будет левосторонней (располагающейся слева от графика) вертикальной асимптотой.
, будет левосторонней (располагающейся слева от графика) вертикальной асимптотой.
Кроме того, функция имеет горизонтальную асимптоту у=0, потому что

Для вычисления последнего предела использовали правило Лопиталя, которое используют для раскрытия неопределенностей вида  или
или  .
.
|
|

 (4)
(4)
График этой функции приведен на рис. 9.

рис. 9.
.
Пример 5. Исследовать функцию  согласно данному плану.
согласно данному плану.
1.а) область существования функции исключает точку х = -1, поэтому 
б) Рассмотрим односторонние пределы вблизи точки разрыва.
 ,
,  . следовательно, в т. х = 1 функция претерпевает разрыв 2-ого рода и, следовательно, имеет вертикальную асимптоту.
. следовательно, в т. х = 1 функция претерпевает разрыв 2-ого рода и, следовательно, имеет вертикальную асимптоту.
2.а) Четность проверим по условию.  . Следовательно, функция общего вида.
. Следовательно, функция общего вида.
б) Корни функции: 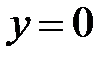 , если
, если  , т.е.
, т.е.  – корень. Т.е. начало координат О
– корень. Т.е. начало координат О  является единственной точкой, где график функции пересекает обе оси.
является единственной точкой, где график функции пересекает обе оси.
в) Интервалы монотонности и критические точки найдем, используя соответствующие признаки для первой производной.  .
.
 , если
, если  и
и  , т.е.
, т.е.  .
.
Соответствующие интервалы монотонности
 ,
,  ,
,  ,
, 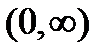
На первом интервале функция возрастает, т.к.  ,
,
на втором убывает, т.к.  . Следовательно, функция имеет максимум в точке (-2, -4).
. Следовательно, функция имеет максимум в точке (-2, -4).
На третьем 
 функция убывает, на четвертом
функция убывает, на четвертом 
 функция возрастает, поэтому точка (0,0) является точкой минимума.
функция возрастает, поэтому точка (0,0) является точкой минимума.
3.Найдем интервалы выпуклости, вогнутости и точки перегиба, используя производную 2 порядка. 
 .
.
 , точек перегиба нет, т.к. числитель этой дроби отличен от нуля. Поэтому определим знак
, точек перегиба нет, т.к. числитель этой дроби отличен от нуля. Поэтому определим знак  на интервалах непрерывности.
на интервалах непрерывности.  кривая выпукла,
кривая выпукла,
 ,
,  кривая вогнута.
кривая вогнута.
4. Как показано в п. 1.б) функция имеет вертикальную асимптоту. Её уравнение х = -1 т.к. именно в этой точке функция претерпевает бесконечный разрыв 2-ого рода.
Определим наличие наклонной, для чего.воспользуемся формулами (3) и правилом Лопиталя (4) для вычисления пределов.
 ,
,
 .
.
Таким образом, прямая  является наклонной асимптотой при
является наклонной асимптотой при  .
.
Для правильного построения графика функции и асимптоты найдем разность 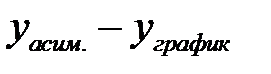 при
при  .
.

То есть, если 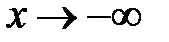 , то асимптота располагается выше графика функции, если
, то асимптота располагается выше графика функции, если  , то ниже. Строим график
, то ниже. Строим график
 .
.
6.2.Вопросы для самоконтроля
1. Если в точке максимума функция дифференцируема, то в этой точке её производная обязательно…
1) равна нулю 2) больше нуля
3) меньше нуля 4) равна
2. График производной  изображен на рисунке 1.
изображен на рисунке 1.
| x |
| y |
| a |
| b |
| c |
| f′(x) |
рис.1
I) Сколько точек экстремума может иметь эта функция?
1) 0. 2) 1 3) 2 4) 3.
II) В какой точке функция f(x) имеет максимум?
1) х=0 2) х = а 3) х = b 4) х = с
III). В какой точке функция f(x) имеет минимум?
1) х = 0 2) х = а 3) х = b 4) х = с
3. Минимальное значение функции  на отрезке
на отрезке  равно …
равно …
|
|
а)  б)
б)  в)
в)  4)
4) 
4. График производной  изображен на рисунке 1. Тогда функция f(x) может иметь точку перегиба при…
изображен на рисунке 1. Тогда функция f(x) может иметь точку перегиба при…
1) х = 0 2) х = а 3) х = b 4) х = с
5. Производная функции имеет вид  . Тогда количество точек перегиба графика функции
. Тогда количество точек перегиба графика функции  равно …
равно …
1)  2)
2)  3)
3)  4)
4) 
6. Уравнение горизонтальной асимптоты графика функции  имеет вид…
имеет вид…
1)  2)
2)  3)
3)  4)
4) 
Ответы. 1). 1 вариант ответа 2). I – 2 вариант, II- 3 вариант, III– 2 вариант.
3. 1 вариант 4. 4 вариант 5. 1 вариант 6. 2 вариант
Задания для аудиторных занятий
1.Найти интервалы монотонности и экстремумы заданных функций.
1.  2.
2. 
 3.
3. 
 2.Найти скорость и ускорение заданных функций в т. х =0
2.Найти скорость и ускорение заданных функций в т. х =0

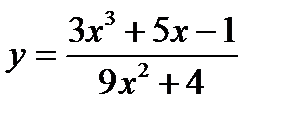
3.Исходя из геометрической характеристики производной первого порядка, определить для данных функций точки, где касательная параллельна оси ОХ. 

4. Найти наибольшее и наименьшее значение функций на заданном отрезке.
1) у 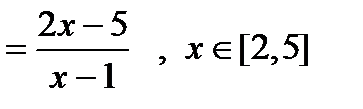 2)
2)  3)
3) 
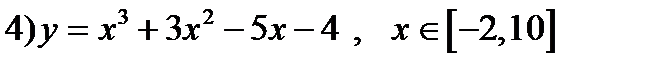
5. Определить количество и вид асимптот, которые имеют данные функции.
1)  , 2)
, 2)  ,
,
3)  , 4)
, 4) 
6. Исследовать функции методами дифференциального исчисления. Построить графики.
1.  2.
2.  3.
3. 
4.  5.
5. 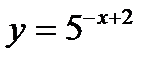

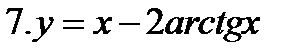

6.4. Контрольное задание № 5
Прибыль с оборота некоторой фирмы за календарный год описан эмпирической формулой у(х) = f(x), где дате 1 января соответствует точка х= 0, и 31 декабря - т. х =12. Найти:
1. Наибольшее и наименьшее значение прибыли в течение года.
2. Абсолютное (в д. ед.) и относительное (в процентах) приращения прибыли за указанный период.
В первой строке указан вид эмпирической зависимости (формула). Во второй строке - варианты и временной период в месяцах. Так, отрезок [0,5]
означает срок с 1 января по 31 мая.

а) 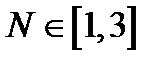
 ; б)
; б) 
 ; в)
; в) 



а) 
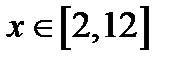 ; б)
; б) 
 ; в)
; в) 


а) 
 ; б)
; б) 
 ; в)
; в) 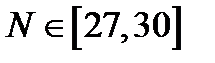


а) 
 ; б)
; б) 
 ; в)
; в) 

Решение демонстрационноговарианта
Прибыль с оборота некоторой фирмы за календарный год описан эмпирической формулой
у(х) = 1/3x 3 -11/2 x2 +24x +10, где 1 января соответствует точке х= 0, и 31 декабря - т. х =12.
Найти:
1. Наибольшее и наименьшее значение прибыли в течение года.
2. Абсолютное (в д. ед.) и относительное (в процентах) приращения прибыли за указанный период.
Решение. Найдем экстремальные точки:



Решим это квадратное уравнение по формуле



Т.к. ветви параболы у (х) = х2 -11х+24 направлены вверх, то меньший корень Х1 = 3 отделяет интервал ее положительных значений от интервала отрицательных, поэтому точка х1 = 3 является точкой максимума.
|
|
Тогда т. х2 = 8 будет являться точкой минимума.
Найдем значения исходной функции на концах отрезка и в экстремальных точках:



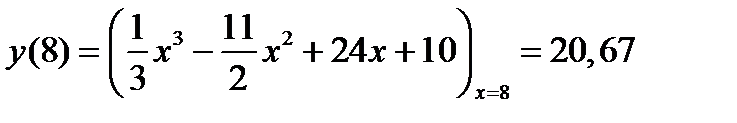
Полученные данные говорят о том, что наименьшее значение прибыли было на 1 января, а наибольшее – на 31 декабря.
Найдем абсолютное и относительное приращения прибыли за год:
 .
. 
Первообразная функции
Неопределенный интеграл
7.1. Основные понятия и определения.
Пусть дана некоторая функция 
 . По правилу предельного отношения приращений
. По правилу предельного отношения приращений  мы находили новую функцию
мы находили новую функцию  , которую назвали производной, а операцию нахождения производной -дифференцированием.
, которую назвали производной, а операцию нахождения производной -дифференцированием.
В физике производная характеризует скорость изменения пути по времени. Если по известной скорости следует определить путь, то приходим к обратной задаче, которая формулируется так:
Дана производная некоторой функции, нужно найти исходную для нее, или первообразную.
Определение 1. Функция F (x) называется первообразной для функции f (x) на некотором интервале, если для всех x из этого интервала выполняется равенство:
 . (1)
. (1)
Если F (x) - первообразная для функции f (x), то и функция F (x)+ C, где C – произвольная постоянная, также будет первообразной для функции f (x), т.к.

Отсюда следует, что если функция f (x) имеет хотя бы одну первообразную, то она будет иметь бесконечно много первообразных, отличающихся друг от друга на постоянную С. Для того, чтобы определить ее значение в конкретном случае, задают начальные условия - требование, чтобы график первообразной функции проходил через заданную точку М0(х0, у0).
Определение 2. Множество всех первообразных для некоторой функции f (x) называется неопределенным интегралом и обозначается символом
 . (2)
. (2)
Символ ò называют знаком интеграла, он говорит о том, что мы ищем первообразные для f (x). Поэтому операцию отыскания всех первообразных называют интегрированием. Например, первообразными для функции х2 являются функции  , что записывается так:
, что записывается так:
 , так как
, так как 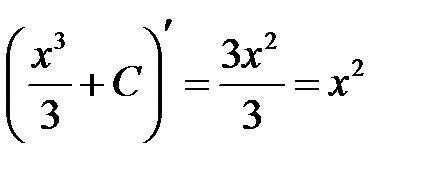
Из определения неопределенного интеграла следуют два свойства
1.  .
.
2. 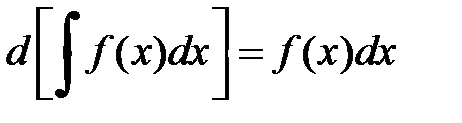 .
.
Таблица интегралов элементарных функций.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 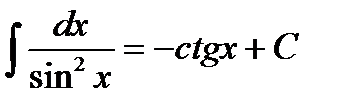
10. 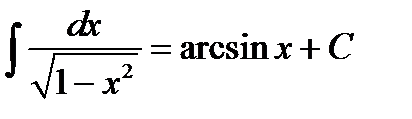
11. 
12. 
13. 
. 14. 
Эта таблица следует из таблицы производных для элементарных функций. Как и в дифференцировании для вычисления неопределенных интегралов есть аналогичные правила:
1. 
 , - постоянный множитель можно вынести за знак неопределенного интеграла;
, - постоянный множитель можно вынести за знак неопределенного интеграла;
2. 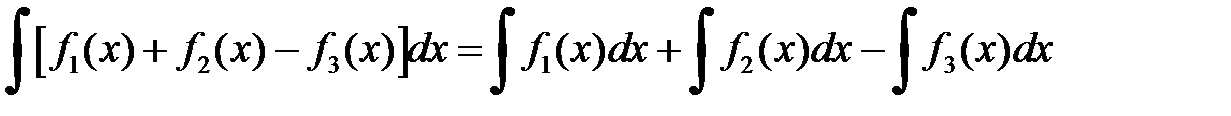 - неопределенный интеграл от алгебраической суммы конечного числа слагаемых равен сумме неопределенных интегралов от каждого слагаемого в отдельности;
- неопределенный интеграл от алгебраической суммы конечного числа слагаемых равен сумме неопределенных интегралов от каждого слагаемого в отдельности;
Правил интегрирования произведения и частного нет.
|
|
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!