

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
1.  7.
7. 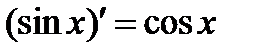
2.  8.
8. 
3.  9
9 
4.  10.
10. 
5.  11
11 
6.  12.
12. 
Пример 1. Вычислить производные следующих функций:
1)  .
.
Решение. Здесь главное действие – сумма, поэтому по правилу 4  .
.
По правилу 3 вынесем постоянные за знаки производных:
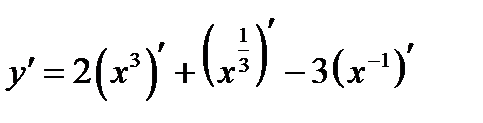
К первому слагаемому применим формулу 2 из таблицы производных, ко второму – формулу 3, к третьему - формулу 4. Получим:
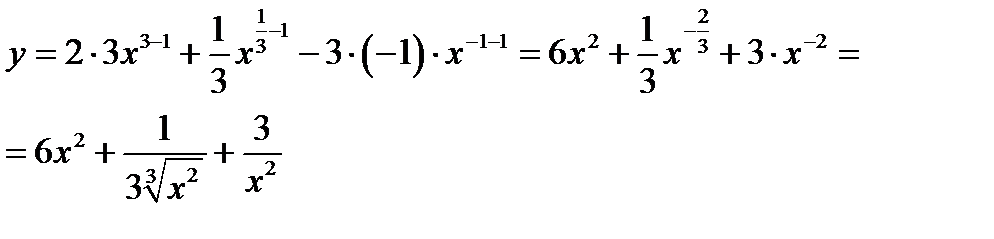 .
.
2)  .
.
Решение. Здесь тоже главное действие сумма, но второе слагаемое представляет собой частное, к которому применим правило 6, а третье – произведение, к которому применим правило 5: 
Дифференцирование сложной функции
Если  ,
,  , тогда
, тогда  называется сложной функцие й, где g(x) - промежуточный аргумент.
называется сложной функцие й, где g(x) - промежуточный аргумент.
Например:  - сложная в указанном смысле функция, у которой промежуточный аргумент
- сложная в указанном смысле функция, у которой промежуточный аргумент  .
.
Пусть для функций 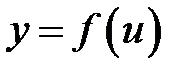 и
и  , существуют производные
, существуют производные  и
и  . Тогда сложная функция
. Тогда сложная функция  имеет производную
имеет производную  , которая находится по формуле:
, которая находится по формуле:
 ,(2)
,(2)
Другими словами производная  равна произведению производных всех функций по промежуточным аргументам. Эта формула приведена в таблице 1 под номером 7.
равна произведению производных всех функций по промежуточным аргументам. Эта формула приведена в таблице 1 под номером 7.
Если промежуточных функций больше, то в правой части формулы 2, добавляются дополнительные сомножители. Для удобства вычислений можно выстраивать цепочку всех промежуточных функций и от каждой брать производные, используя соответствующие правила и формулы.
Пример 2. Вычислить производные сложных функций:
1) 
Решение: Цепочка выглядит так:  Т.к.
Т.к.  , то
, то 

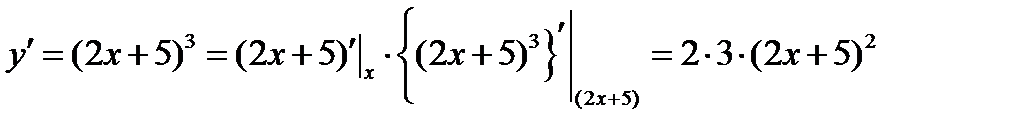
2) 
Решение: 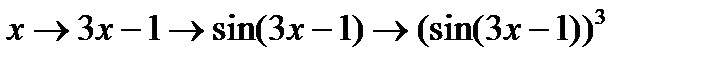


3) 
Решение: Цепочка сложности 
 =
= 
= 

При введении понятия «производная» был использована ее физическая характеристика как скорость изменения функции. Тогда ускорение будет описывать производная от производной или производная второго порядка: 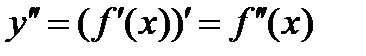 . Производные второго порядка вычисляются по тем же правилам и формулам, что производные первого порядка. Также можно вычислить производные любого порядка.
. Производные второго порядка вычисляются по тем же правилам и формулам, что производные первого порядка. Также можно вычислить производные любого порядка.
|
|
Вопросы для самоконтроля
1.Закон движения материальной точки имеет вид  , где
, где  - координата точки в момент времени
- координата точки в момент времени  . Тогда скорость точки при
. Тогда скорость точки при  равна …
равна …
1)  2)
2)  3)
3)  4)
4) 
2. Производная функции  равна…
равна…
1)  2)
2) 
3)  4)
4) 
3.Производная произведения 
 равна …
равна …
1)  2)
2) 
3) 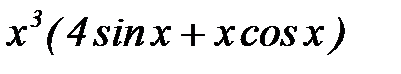 4)
4) 
4. Производная частного  равна …
равна …
1)  2)
2)  3)
3)  4)
4) 
5.Установите соответствие между функцией и её производной:
1.  A)
A) 
2.  B)
B) 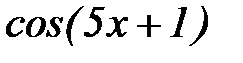
3.  C)
C) 
D) 
E) 
Ответы. 1) 4, 2) 1, 3) 4, 4) 4,
5) 1 – Е, 2 – С, 3 – А.
Задания для аудиторной работы
Пример 1 Вычислить производные функций
1  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
Пример 2. Найти скорость и ускорение следующих функций в заданных точках.
1. 1)y = 21/ x х=1, 2) y = ln ctg 2x х=1,
2. 3)y = x arctg x х=0, 4) y = ex cos x х=0,
3. 5) y = x2(1+ln x) х = е, 6) y = e–x sin x х=0,
5.4. Контрольные задания № 7
Вычислить производные данных функций.
1.
а)  б).
б).  в)
в) 
2.
 б).
б).  в)
в) 
3.
а).  б)
б)  в)
в) 
4.
а)  б)
б)  в)
в)  .
.
5.
а)  б)
б) 

6.
а)  б)
б)  в)
в) 
7.
а) 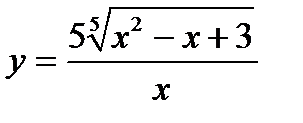 б)
б)  в)
в) 
8.
а)  б)
б)  в)
в) 
9.
а).  б).
б).  в).
в). 
10. а).  б)
б)  в)
в) 
11.
а)  б).
б). 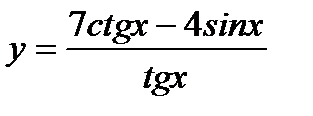 в).
в). 
12.
а).  б).
б).  в)
в) 
13.
а)  б).
б). 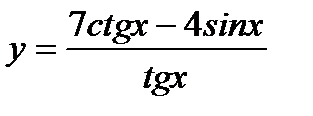 в)
в) 
14.
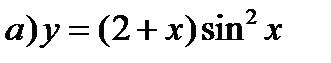

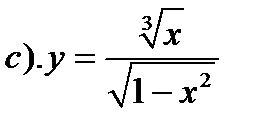
15.
  
|
16.
 б)
б)  в)
в) 
17.
а) 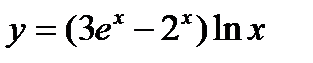 б).
б).  в).
в). 
18.
а)  - 3х 2 б).
- 3х 2 б).  в).
в). 
19.
а)  б).
б).  . в).
. в). 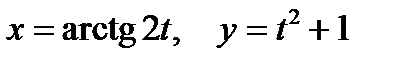
20.

| 20. |
Исследование функций
Известно, чтолюбое явление: конъюнктура рынка, сезонные колебания спроса на товар, прибыль и т.д. вначале изучаются с количественной стороны, а потом описывают функциональной зависимостью, т.е. формулой.
Например, анализ спроса на купальники показал, что он подчиняется формуле  , где
, где 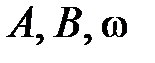 – некоторые постоянные, не меняющиеся в течении лет,
– некоторые постоянные, не меняющиеся в течении лет,  – время (мес.). На основании приведенной формулы можно выяснить, при каких значениях
– время (мес.). На основании приведенной формулы можно выяснить, при каких значениях 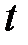 спрос в будущем будет максимальным и каких именно величин он достигнет, при каких – минимальным, а также решать другие вопросы. Именно они входят в понятие «исследование функции».
спрос в будущем будет максимальным и каких именно величин он достигнет, при каких – минимальным, а также решать другие вопросы. Именно они входят в понятие «исследование функции».
Все исследования проводятся по общему плану.
План исследования функции.
1. Область определения функции. Выявление точек разрыва, поведение функции вблизи точек разрыва
|
|
2. Симметрия, точки пересечения с осями координат.
3. Интервалы возрастания и убывания, точки экстремумов
4. Интервалы выпуклости и вогнутости графика функции, точки перегиба
5. Асимптоты: вертикальные, горизонтальные, наклонные.
6.Построение графика.
Первые два пункта детально изучались как в школьном, так и настоящем курсе. Поэтому рассмотрим пункты 3, 4, 5.
6.1.Основные понятия и определения
Интервалы возрастания и убывания функции, точки экстремумов
Определение 1. Функция  , непрерывная на интервале
, непрерывная на интервале  называется возрастающей, если большему значению аргумента
называется возрастающей, если большему значению аргумента 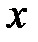 соответствует большее значение
соответствует большее значение  , т. е. из выполнения неравенства
, т. е. из выполнения неравенства  следует выполнение неравенства
следует выполнение неравенства  .
.
Определение 2. Функция  , непрерывная на интервале
, непрерывная на интервале  называется убывающей, если большему значению аргумента
называется убывающей, если большему значению аргумента  соответствует меньшее значение
соответствует меньшее значение  , т. е. из выполнения неравенства
, т. е. из выполнения неравенства 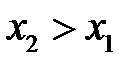 следует выполнение неравенства
следует выполнение неравенства 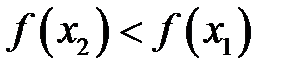 .
.
Признаки возрастания и убывания функции.
1.Если на отрезке 
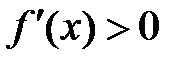 , функция
, функция  возрастает.
возрастает.
2.Если на отрезке 
 , функция
, функция  убывает
убывает
Определение 3. Пусть функция 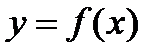 непрерывна и дифференцируема (имеет производную) на отрезке
непрерывна и дифференцируема (имеет производную) на отрезке  . Точка
. Точка  называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции  , если для всех х из некоторой
, если для всех х из некоторой 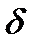 - окрестности точки х0 выполняется неравенство
- окрестности точки х0 выполняется неравенство  , (
, (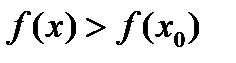 ). Их называют точками локального экстремума (см. рис.8.1 и 8.2)
). Их называют точками локального экстремума (см. рис.8.1 и 8.2)
Признак существования экстремума. Пусть функция  дифференцируема на отрезке
дифференцируема на отрезке  . Для того, чтобы в точке
. Для того, чтобы в точке  функция имела экстремум, необходимо, чтобы производная в этой точке была равна нулю
функция имела экстремум, необходимо, чтобы производная в этой точке была равна нулю  (или не существовала) и достаточно, чтобы
(или не существовала) и достаточно, чтобы  меняла свой знак. Причем, если производная
меняла свой знак. Причем, если производная  при переходе через
при переходе через  слева направо меняет знак с (+) на (–), то точка х0 – точка максимума, если с (–) на (+) – точка минимума.
слева направо меняет знак с (+) на (–), то точка х0 – точка максимума, если с (–) на (+) – точка минимума.
Из школьного курса математики известна геометрическая интерпретация производной. А Она численно равна тангенсу угла наклона касательной к графику функции в точке х = а кположительному направлению оси ОХ. Если угол острый, то функция возрастает, если тупой – убывает. В точках экстремумов касательная параллельна оси ОХ либо оси ОУ, либо ее нельзя провести. Функции, изображенные на рис 1 и 5, имеют минимум, на рисунках 2, и 5 - максимум. Если ка- сательная пересекает кривую (рис.3),, то экстремума нет 

|
|
рис.1 рис.2 
рис.3 рис. 4 рис.5
Порядок нахождения экстремумов функции:
1. Находим производную функции  и решаем уравнение
и решаем уравнение  . К корням этого уравнения добавляем точки, в которых производная не существует. Такие точки называются критическими.
. К корням этого уравнения добавляем точки, в которых производная не существует. Такие точки называются критическими.
2. Определяем знаки  вблизи критических точек на всех интервалах непрерывности.
вблизи критических точек на всех интервалах непрерывности.
3. Делаем выводы о наличии (или отсутствии) экстремумов и интервалов возрастания и убывания. Их называют интервалами монотонности.
4. Находим ординаты экстремальных точек из уравнения  , где
, где  – абсцисса точки экстремума.
– абсцисса точки экстремума.
Пример 1. Определить, будет ли функция 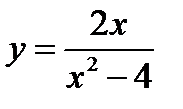 иметь точки экстремумов, а также найти интервалы монотонности функции,
иметь точки экстремумов, а также найти интервалы монотонности функции,
Решение. Найдем область допустимых значений функции, потребовав неравенство нулю знаменателя:  ,
,
откуда 
Найдем первую производную:
 .
.
Найдем экстремальные точки:
 , т. к.
, т. к. 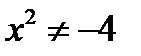 , и
, и 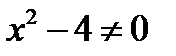 , поэтому экстремумов нет.
, поэтому экстремумов нет.
Определим знак  на каждом из интервалов непрерывности
на каждом из интервалов непрерывности  . Поскольку
. Поскольку  и
и  для любых
для любых  , и то знак
, и то знак  будет всегда отрицательным. То есть на всех интервалах непрерывности наша функция будет убывать, что и демонстрирует рис. 6.
будет всегда отрицательным. То есть на всех интервалах непрерывности наша функция будет убывать, что и демонстрирует рис. 6.
Рассмотрим поведение функции вблизи точек разрыва  и
и  . Для этого найдем односторонние пределы при
. Для этого найдем односторонние пределы при  и
и  .
.



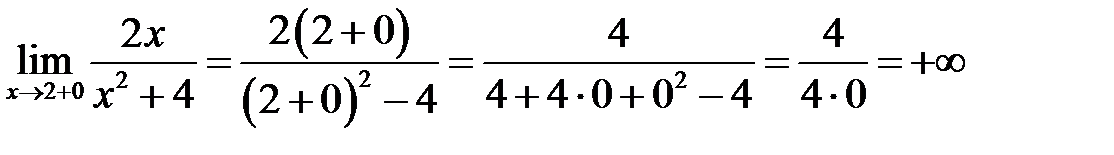
Начертим схематический график

рис. 6
|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!