Рассмотрим задачу о распространении тепла в стержне, концы которого поддерживаются при нулевой температуре. Задача состоит в отыскании решения уравнения теплопроводности:
ut = a 2 uxx
при граничных условиях:
u | x =0 = 0; u | x = l = 0,
и при начальном условии:
u | t =0 = j (x),
где j (x) – непрерывна, имеет кусочно-непрерывную производную и обращается в ноль при x = 0 и x = l.
Будем решать эту задачу методом Фурье. Согласно методу Фурье ищем сначала частные решения уравнения в виде произведения двух функций:
u (x, t) = X (x)× T (t).
Подставляя u (x, t) в исходное уравнение, имеем:
X (x)× T' (t) = a 2 T (t) X'' (x).
Разделяем переменные:
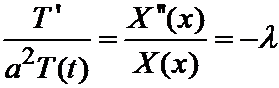
получаем два уравнения:
T' (t) + a 2 lT (t) = 0,
X'' (x) + lX (x) = 0.
Чтобы получить нетривиальное решение уравнения в виде произведения двух функций, удовлетворяющее граничным условиям, необходимо найти нетривиальное решение уравнения:
X'' (x) + lX (x) = 0,
удовлетворяющего граничным условиям:
X (0) = 0; X (l) = 0.
Таким образом, для определения функций X (x) мы приходим к задаче о собственных значениях, т.е. приходим к следующей задаче: найти такие значения параметра l, при которых существует нетривиальные решения, удовлетворяющие граничным условиям.
Те значения l, при которых задача имеет нетривиальные решения, называются собственными числами, а сами эти решения – собственными функциями.
Задача нахождения собственных чисел и собственных функций называется задачей Штурма-Лиувилля.
Решение уравнения:
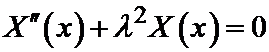 .
.
удовлетворяющего граничным условиям:
X (0) = 0; X (l) = 0.
мы с Вами уже находили, когда рассматривали метод Фурье для уравнения колебаний струны.
Это решение имело следующий вид:
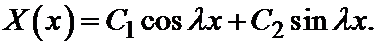
Далее, как и раньше подставляем граничные условия:
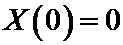 =>
=> 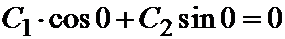 => C 1=0,
=> C 1=0,
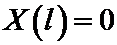 =>
=> 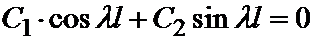 => C 2×sin ll =0.
=> C 2×sin ll =0.
Последнее равенство возможно при sin ll =0.
То есть при 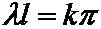 (k= ±1; ±2;….)
(k= ±1; ±2;….)
Итак, если 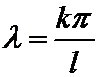 , т.е.
, т.е. 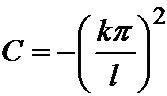 , то существуют решения уравнения теплопроводности, не равные тождественно нулю.
, то существуют решения уравнения теплопроводности, не равные тождественно нулю.
Решение, отвечающее некоторому фиксированному k обозначим через Xk (x). Оно имеет вид:
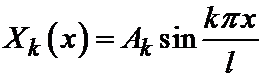 ,
,
Рассмотрим теперь второе уравнение:
T '(t)+ a 2 lT (t)=0.
Это уравнение решается. Разделяем переменные
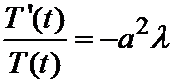 ; ln T (t)=- a 2 l + C;
; ln T (t)=- a 2 l + C; 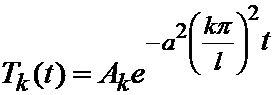 ,
,
где Ak – произвольные постоянные. Итак, все функции вида:
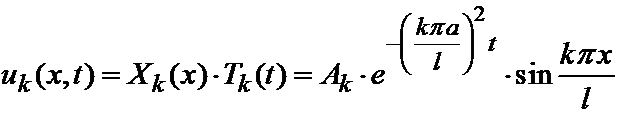
удовлетворяют уравнению теплопроводности и граничным условиям при любых Ak =const. Составим ряд:
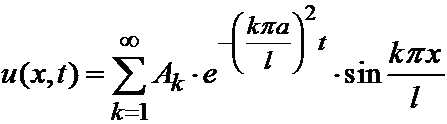 .
.
Требуя выполнение начального условия u | t =0= j (x), получим:
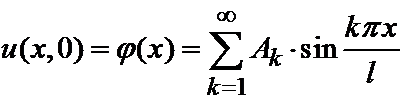 .
.
Написанный ряд представляет собой разложение заданной функции j (x) в ряд Фурье по синусам в промежутке (0, l). Коэффициенты Ak вычисляются по известной формуле:
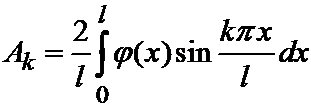 .
.
Так как мы предположили, что функция j (x) непрерывна, имеет кусочно-непрерывную производную и обращается в ноль при x =0 и x = l, то ряд
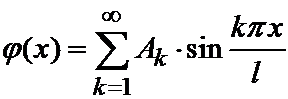
с коэффициентами Ak равномерно и абсолютно сходится к j (x), что известно из теории тригонометрических рядов.
Итак, решение первой краевой задачи для уравнения теплопроводности выписывается следующим образом:
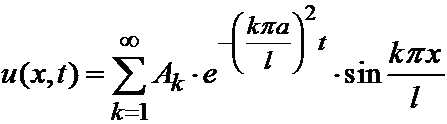
где
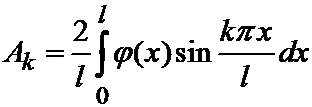 .
.
коэффициенты Фурье начальных данных.



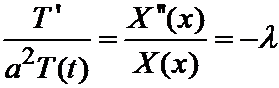
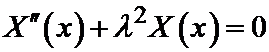 .
.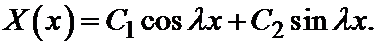
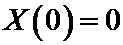 =>
=> 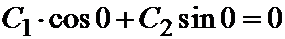 => C 1=0,
=> C 1=0,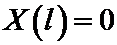 =>
=> 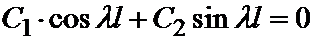 => C 2×sin ll =0.
=> C 2×sin ll =0.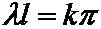 (k= ±1; ±2;….)
(k= ±1; ±2;….)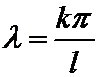 , т.е.
, т.е. 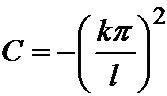 , то существуют решения уравнения теплопроводности, не равные тождественно нулю.
, то существуют решения уравнения теплопроводности, не равные тождественно нулю.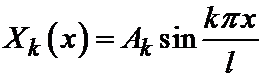 ,
,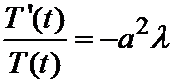 ; ln T (t)=- a 2 l + C;
; ln T (t)=- a 2 l + C; 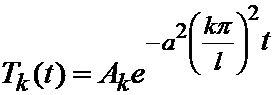 ,
,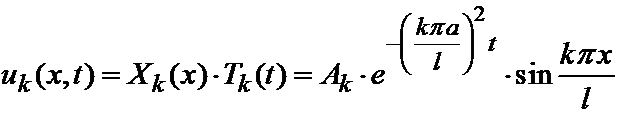
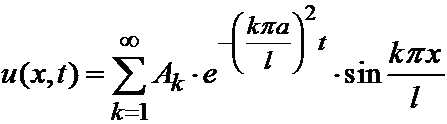 .
.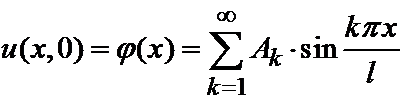 .
.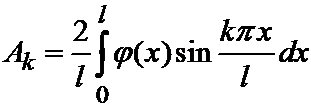 .
.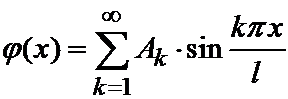
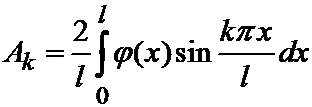 .
.


