

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Приращение функции
Определение 1. Приращением величины называется разность между новым значением величины и старыми обозначается буквой Δ.
ΔN = N2 – N1.
Другими словами, приращение величины показывает на сколько изменилась величина.
Определение 2. Приращением аргумента (функции) называется разность между новым значением аргумента (функции) и старым и обозначается буквой Δ.
Δх = х2 – х1 - приращение аргумента;
Δу = у2 – у1 - приращение функции.
Если известны начальное значение величины N и ее ΔN, то можно найти ее новое (наращенное) значение N2 = N + ΔN.
Примеры
1. Найти приращение функции у=2х2 – 1, если х изменился от 3 ед. до 3,5 ед.
Решение
Найдем значение функции у1 при х1=3: у1=2∙32 – 1=17 ед,
затем найдем у2 при х2 = 3,5: у2 = 2∙3,52 – 1 = 23,5 ед.
Тогда Δу = у2 – у1 = 23,5 – 17 = 6,5 ед.
Производная функции
Определение Производной функции называется предел отношения приращения функции Δy к приращению аргумента Δx, когда приращение аргумента стремится к нулю, и обозначается 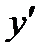 .
.
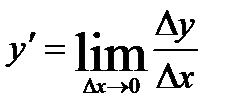
Производная производной первого порядка называется производной второго порядка.
y’’=(y’)’
Формулы дифференцирования
1. (С)′ = 0 11. (sin x)′ = cos x
2. (х)′ = 1 12. (cos x)′ = - sin x
3. (u + v – w)′ = u′ + v′ - w′ 13. (tg x)′ = 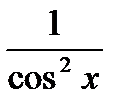
4. (u∙v)′ = uv′ +vu′ 14. (ctg x)′ = 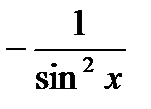
5. (Cx) = C 15. (ln x)′ = 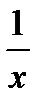
6. (Cu)′ = C(u)′ 16. (lg x)′ = 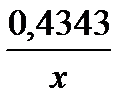
7. (x m)′ = m∙x m – 1 17. (a x)′ = a x∙ln x
8. 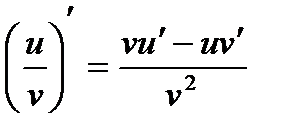 18. (e x)′ = e x
18. (e x)′ = e x
9. 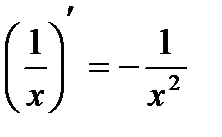 19. (arcsin x)′ =
19. (arcsin x)′ = 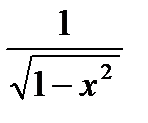
10. (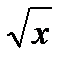 )′ =
)′ = 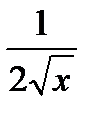 20. (arctg x)′ =
20. (arctg x)′ = 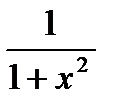
Замечание. Нахождение производной функции называется дифференцированием функции.
Примеры
Продифференцировать функции:
1. у = 2х3 – 4х2 + 5х – 3
Решение. По правилу (3) имеем:
у′ =(2х3)′ - (4х2)′ + (5х)′ – (3)′
|
|
Применяя к первым трем слагаемым правило (6), а к последнему – правило (1), получим:
у′ =2(х3)′ - 4(х2)′ + 5(х)′ – 0.
По правилу (5) и (2) имеем:
у′ =2∙3х2 - 4∙2х + 5 ∙1 = 6х2 - 8х + 5.
2. у = (х2 + 1)(2х + 3)
Решение. По правилу (4) имеем:
у′ = ((х2 + 1)(2х + 3))′ = (х2 + 1)(2х + 3)′ + (х2 + 1)′ (2х + 3)
По правилу (3) имеем:
у′ =(х2 + 1) ( (2х)′ + (3)′ ) + ((х2)′ + (1)′ ) (2х + 3)
По правилам (6), (2), (1) и (7)
у′ =(х2 + 1)(2 + 0 ) + (2х + 0 ) (2х + 3) =2х2 + 2 + 4х2 + 6х = 6х2 +6х + 2.
3. 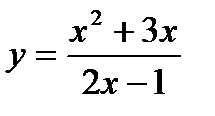
Решение. По правилу (8) имеем:
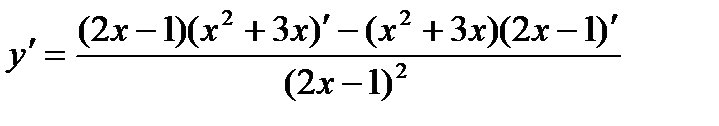
По правилам (7), (5), (1):
= 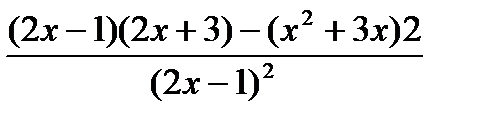
раскроем скобки и приведем подобные: 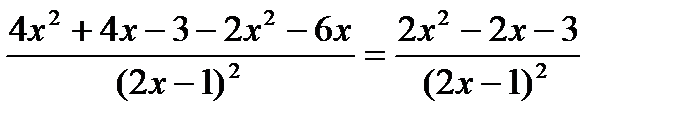 .
.
4. 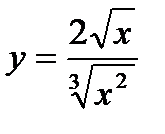
Решение. Упростим функцию:
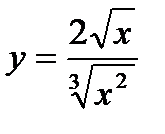 =
= 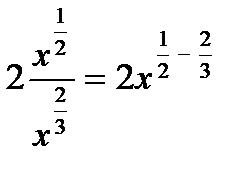 =
= 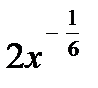
по правилу дифференцирования степенной функции (8) получим
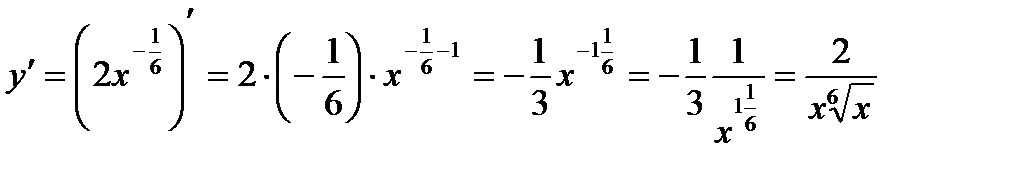
5. 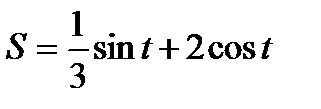
Решение. По правилу (8) имеем:
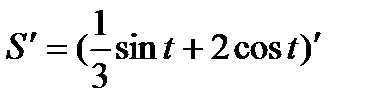 =
= 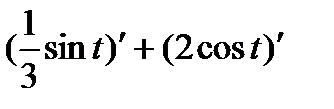 =
=
По правилу (6), (11), (12) имеем:
= 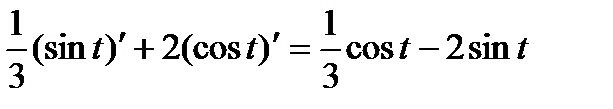
Практическая работа 1
"Дифференцирование функций и построение графиков"
Цель работы: формировать умения по выполнению дифференцирования функций и применению ее к решению задач
Основные понятия
Определение 1. Функция называется простой, если над аргументом выполняется одно функциональное действие.
Определение 2. Функция называется сложной, если над аргументом выполняется более одного функционального действия.
Замечание. Путем замены переменной сложную функцию можно свести к простой, но уже относительно новой переменной.
Например
Простая функция Сложная функция Замена Простая функция
y = x5 y =(3x – 2)5 u = 3x – 2 y = u5
y = sin x y = sin 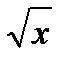 u =
u = 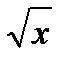 y = sin u
y = sin u
y = ln x y = ln cosx u = cosx y = ln u
y = 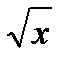 y =
y = 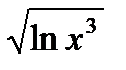 u = ln x3 y =
u = ln x3 y = 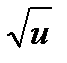
y = f(x) y = f(φ(x)) u = φ(x) y = f(u)
Производная сложной функции
Производная сложной функции равна произведению производной данной функции по промежуточному аргументу (замене) на производную промежуточного аргумента (замены) по основному.
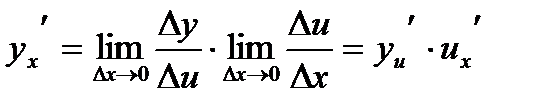
|
(1)
Например. Найти производную функции y = (3x2 – 5)3.
Решение. y ’ = ((3x2 – 5)3) ’ Функция сложная.
Заменой переменной обозначим u = (3x2 – 5).
Тогда функция примет вид y = u3.
По (1) ищем ее производную в таком виде: y ’ = (u3) ’= 3u2∙u ’.
Вернемся к старой переменной: y ’ = (u3) ’= 3u2∙u ’ = 3 (3x2 – 5)2(3x2 – 5) ’
|
|
Взяв производную скобки, окончательно получим:
y ’ = 3 (3x2 – 5)2∙6х = 18х(3x2 – 5)2.
Замечание.
1) Для введения промежуточной переменной u необходимо помнить, что функция должна стать простой, т.е. иметь одно действие. Для этого необходимо разобраться в порядке действий в данной функции, найти последнее и оставить его, т.е. обозначить за u все, что есть, до последнего действия.
2) За u не обозначается постоянное число, помнить, что u – это функция.
3) За u не обозначается все выражение, т.к. тогда не будет ни одного действия.
Например.
1) y = 2(x – 1)5, u = (x – 1) 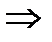 у = 2u5
у = 2u5
2) y = 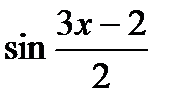 , u =
, u = 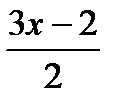
 y = sin u
y = sin u
3) 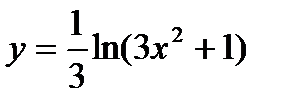 , u =
, u = 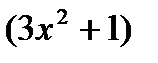
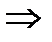 y =
y = 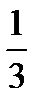 ln u
ln u
Примеры
Продифференцировать функции
1) y = (x3 – 4x + 1)3
Решение
Функция сложная, т.к. над аргументом х выполняется несколько действий. Введем промежуточную функцию u = (x3 – 4x + 1), сводящую данную функцию к простой y = u3.
И тогда, по формуле степенной функции (7) получим:
y ’ = (u3) ’= 3u2∙u ’ = 3 (x3 – 4x + 1)2(x3 – 4x + 1) ’ = 3 (x3 – 4x + 1)2(3х2 – 4)
2) 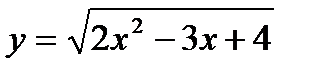
Решение
Функция сложная, т.к. над аргументом х выполняется несколько действий. Введем промежуточную функцию u = 2x2 – 3x + 4,сводящую данную функцию к простой: 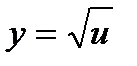 .
.
Тогда, по формуле (10):
(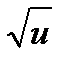 )′ =
)′ = 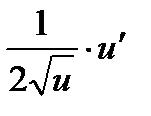 , получим:
, получим:
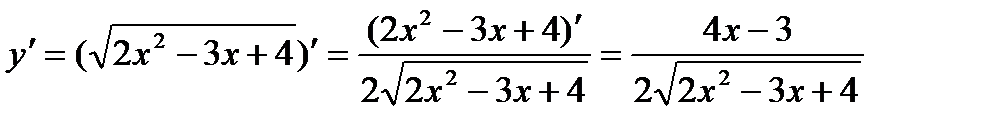
3) 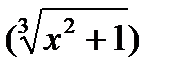
Если дан корень другой степени, то его нужно преобразовать в степень с дробным показателем и затем применить формулу (7).
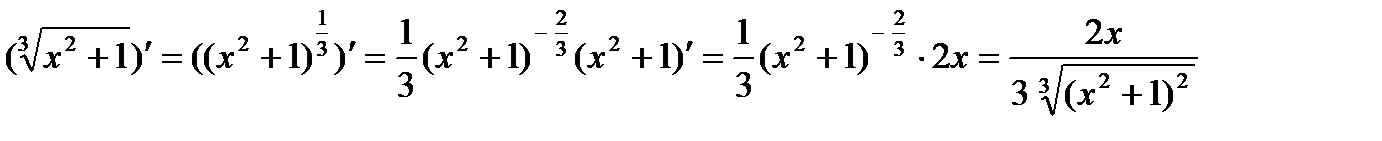
4) 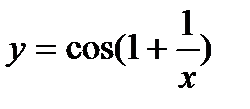
Решение
Функция сложная, введем промежуточную переменную 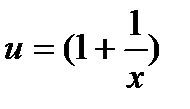 .
.
И по формуле (12):
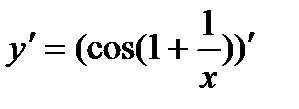
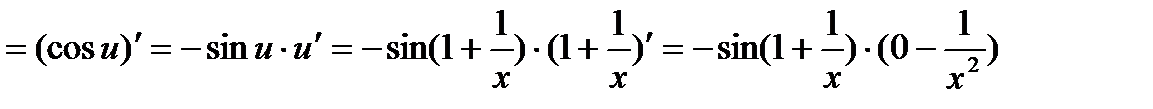 =
=
= 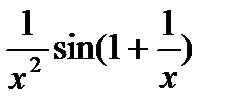
|
|
|

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!