СИСТЕМЫ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ. МОДЕЛИРОВАНИЕ В MATLAB
Омск - 2009
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
«Омский государственный технический университет»
СИСТЕМЫ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ. МОДЕЛИРОВАНИЕ В MATLAB
Лабораторный практикум по дисциплине
«Основы автоматического управления»
Для специальности 200503 «Стандартизация и сертификация»
Омск - 2009
Составитель:
Шендалева Елена Владимировна, канд. техн. наук
Учебное пособие посвящено практическому использованию методов теории автоматического управления, моделированию систем автоматического управления в среде пакета прикладного программного обеспечения MATLAB.
Печатается по решению редакционно-издательского совета Омского государственного технического университета.
Лабораторные работы выполняются в среде программного пакета MATLABÒ и в интерактивной среде SIMULINKÒ. Для выполнения ряда работ необходимо использовать результаты предыдущих работ, для чего необходимо сохранение результатов моделирования.
Matlab – язык высокого уровня, объединяющий численные расчеты, визуализацию и программирование. Simulink представляет пользователю графический интерфейс для конструирования моделей из стандартных блоков.
Лабораторная работа № 1
Roots(p).
Задание
1. В соответствии с индивидуальным заданием в пакете Simulink построить модели типовых звеньев. Определить временные характеристики типовых звеньев при подаче ступенчатого и одиночного импульсного (d-функции) входного сигнала. Моделирование одиночного импульсного сигнала осуществить с помощью последовательного соединения генератора ступенчатого сигнала и дифференцирующего звена.
2. В соответствии с индивидуальным заданием определить временные и частотные характеристики апериодического, инерционно-форсирующего и колебательного звена. Определить влияние на временные и частотные характеристики звеньев их параметров. Определить корни их характеристических уравнений.
3. Выполнить обратные преобразования Лапласа переходных и весовых функций указанных звеньев.
Содержание отчета
1. Переходные и весовые функции типовых звеньев, полученные в пакете Simulink (рис. 1.1, 1.2, 1.3).
2. Значения корней характеристических уравнений передаточных функций апериодического, инерционно-форсирующего и колебательного звеньев.
3. Переходные и весовые функции, амплитудно-частотные, фазо-частотные и амплитудно-фазовые характеристики апериодического звена с анализом влияния коэффициента усиления k и постоянной времени Т.
4. Переходные и весовые функции, амплитудно-частотные, фазо-частотные и амплитудно-фазовые характеристики инерционно-форсирующего звена с анализом влияния коэффициента усиления k и постоянной времени Т.
5. Переходные и весовые функции, амплитудно-частотные, фазо-частотные и амплитудно-фазовые характеристики колебательного звена с анализом влияния коэффициента усиления k и постоянной времени Т 1.
Контрольные вопросы
1. Дифференциальные уравнения и передаточные функции, описывающие типовые динамические звенья.
2. Как создать в пакете Simulink модель реального дифференцирующего звена?
3. Как создать в пакете Simulink модель колебательного звена?
4. Как создать в пакете Simulink модель интегрирующего звена?
5. Как создать в пакете Simulink модель реального дифференцирующего звена?
6. С помощью, какой команды определяют переходные функции?
7. С помощью, какой команды определяются весовые функции?
8. С помощью, какой команды строят ЛАХ и ЛФХ?
9. С помощью, какой команды строят АФХ?
10. С помощью какой команды осуществляют обратное преобразование Лапласа изображения переходной функции?
11. С помощью какой команды осуществляют обратное преобразование Лапласа изображения весовой функции?
12. Напишите программу, позволяющую определять корни характеристического уравнения.
Лабораторная работа №2
Определение коэффициентов дифференциальных уравнений
Лабораторная работа № 3
Лабораторная работа № 4
Моделирование систем автоматического управления
Методом вариации постоянных
Цель работы
1. Аналитическое вычисление фундаментальных матриц при моделировании системы методами прямого, параллельного и последовательного программирования.
2. Решение дифференциальных уравнений методом вариации постоянных.
Теоретическое обоснование
Лабораторная работа выполняется на основе моделей и индивидуального задания лабораторной работы №3.
Непрерывная линейная система также может быть описана дифференциальным векторно-матричным уравнением
 (4.1)
(4.1)
где А – матрица коэффициентов состояний размером k ´ k; В – матрица коэффициентов управления размером k ´ n; С – матрица коэффициентов наблюдения размером m ´ k и D – матрица коэффициентов выхода размером m ´ n; X – вектор состояния (матрица-столбец размером k ´ l); U – вектор управления (матрица-столбец размером n ´ l); Y – вектор наблюдения (матрица-столбец размером m ´ l).
Решение уравнения (4.1) можно выразить через фундаментальные матрицы, определенные несколькими методами.
Первый метод основан на взятии конечного числа элементов разложения
 ,
,
где 
Второй способ основан на аналитическом вычислении матрицы Ф (t).
Преобразование Лапласа векторного дифференциального уравнения  дает s X (s) − X (0) = AX (s). Откуда X (s) [ I s − A ] = X (0) или X (s) = [ I s – A ]-1 X (0), где I – единичная матрица.
дает s X (s) − X (0) = AX (s). Откуда X (s) [ I s − A ] = X (0) или X (s) = [ I s – A ]-1 X (0), где I – единичная матрица.
При применении к обеим частям последнего уравнения обратного преобразования Лапласа X (t) = L -1{[ I s − A ]-1} X (0).
Выражение L -1{[ I s − A ]-1} = e A t = Ф (t) определяет фундаментальную матрицу системы.
Множество решений однородного векторно-матричного дифференциального уравнения  где каждому начальному условию
где каждому начальному условию  соответствует только одно решение дифференциального уравнения, образует N -мерное векторное пространство. Среди множества решений всегда может быть выбрано n линейно независимых. Матрица X (t)[ n ´ n ], столбцами которой являются n линейно независимых решений системы, называется фундаментальной матрицей этой системы дифференциальных уравнений.
соответствует только одно решение дифференциального уравнения, образует N -мерное векторное пространство. Среди множества решений всегда может быть выбрано n линейно независимых. Матрица X (t)[ n ´ n ], столбцами которой являются n линейно независимых решений системы, называется фундаментальной матрицей этой системы дифференциальных уравнений.
Общее решение матричного дифференциального уравнения для известной фундаментальной матрицы Ф (t) определяется формулой Коши (формулой вариации постоянных)
 (4.2)
(4.2)
где l – собственные значения матрицы Ф.
Описание работы
Рассмотрим систему с передаточной функцией (4.3)
 (4.3)
(4.3)
Метод прямого программирования
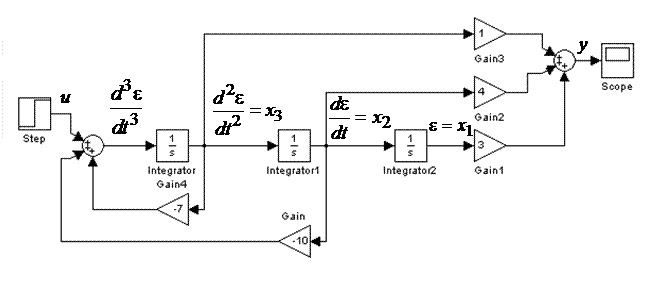
Рис. 4.1. Схема моделирования системы методом прямого программирования
 (4.4)
(4.4)

 C = [3 4 1], D = 0.
C = [3 4 1], D = 0.
Аналитическое вычисление фундаментальной матрицы заключается в определении матрицы состояния A, разности [ I s − A ], нахождении обратной матрицы и применении обратного преобразования Лапласа к каждому элементу обратной матрицы.
В пакете MatLab эти операции выполняются следующим образом.
A=[0,1,0;0,0,1;0,-10,-7] %Матрица состояния А
syms s %Символьная переменная
Is=[s,0,0;0,s,0;0,0,s] %Единичная матрица
F=inv([Is]-[A]) %Обратная матрица в частотной области
F1=ilaplace(F) %Обратная матрица во временной области.
В результате выполнения программы получают фундаментальную матрицу в частотной области
 (4.5)
(4.5)
и во временной области
 (4.6)
(4.6)
Выражение (4.6) получено из (4.5) с помощью обратного преобразования Лапласа применительно к каждому элементу матрицы. В случае нулевых начальных условий X (0) = 0 и нулевой матрицы выхода системы D = 0 первое и второе слагаемое формулы Коши (4.2) равны нулю, откуда
 (4.7)
(4.7)
Фундаментальная матрица в символьной форме выглядит как
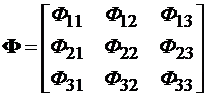 .
.
Для определения подынтегрального выражения (4.7) вычисляют:
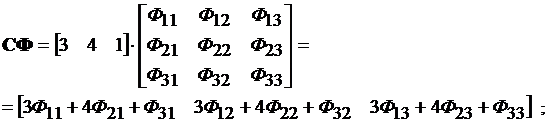
 СФВU = [3 Ф 13 + 4 Ф 23 + Ф 33]×[1] = [3 Ф 13 + 4 Ф 23 + Ф 33] =
СФВU = [3 Ф 13 + 4 Ф 23 + Ф 33]×[1] = [3 Ф 13 + 4 Ф 23 + Ф 33] =
=  .
.
Выходную величину системы определяют из выражения (4.7):

Решение матричного интегрального уравнения


График переходной функции (рис. 4.2) определяют следующим образом
t=0:0.01:1;
y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);
Plot(t,y).

Рис. 4.2. Переходная функция модели, определенная методом прямого программирования
Метод параллельного программирования
При разложении передаточной функции (4.3) методом Хевисайда:
 (4.8)
(4.8)
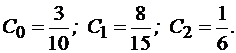 (4.9)
(4.9)
С учетом выражения (4.8) получена схема моделирования (рис. 4.3).

Рис. 4.3. Схема моделирования системы методом параллельного программирования
 (4.10)
(4.10)


 D = 0.
D = 0.
Матрица A при параллельном программировании имеет диагональный вид, что достигается выбором базиса, при котором фазовые координаты не влияют друг на друга.
Определяют фундаментальную матрицу Ф (t):
A=[0,0,0;0,-2,0;0,0,-5] %Матрица состояния
syms s %Символьная переменная
Is=[s,0,0;0,s,0;0,0,s] %Единичная матрица
F=inv([Is]-[A]) %Обратная матрица в частотной области
F1=ilaplace(F) %Обратная матрица во временной области.
Фундаментальная матрица в частотной области
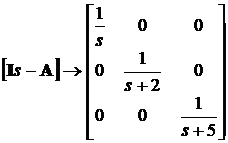
и во временной области





Решение матричного интегрального уравнения


График переходной функции (рис. 4.4) определяют следующим образом
t=0:0.01:1;
y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);
Plot(t,y).
Метод последовательного программирования
Структурную схему для последовательного программирования получают из передаточной функции (4.5), если ее разбить на блоки и для каждого блока представить схему моделирования
 (4.11)
(4.11)
По блочной передаточной функции (4.11) составляют схему моделирования (рис. 4.5)
Из схемы моделирования (рис. 4.5) получена матрица коэффициентов состояния А и матрица коэффициентов наблюдения С
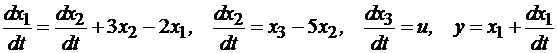
или


Рис. 4.4. Переходная функция модели, определенная методом параллельного программирования
 (4.12)
(4.12)

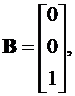 C = [-1 -2 1], D = 0.
C = [-1 -2 1], D = 0.
Определяют фундаментальную матрицу Ф (t):
A=[-2,-2,1;0,-5,1;0,0,0] %Матрица состояния
syms s %Символьная переменная
Is=[s,0,0;0,s,0;0,0,s] %Ввод единичной матрицы
F=inv([Is]-[A]) %Обратная матрица в частотной области
F1=ilaplace(F) %Обратная матрица во временной области.
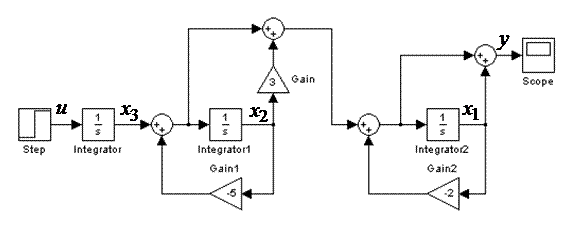
Рис. 4.5 Схема моделирования системы методом последовательного программирования
Фундаментальная матрица в частотной области

и во временной области




Решение матричного интегрального уравнения


График переходной функции (рис. 4.6) определяют следующим образом
t=0:0.01:1;
y=(3/10)*t-(1/12)*exp(-2*t)-(8/75)*exp(-5*t)+(19/100);
Plot(t,y).

Рис. 4.6. Переходная функция модели по методу последовательного программирования
Задание
1. По полученным в лабораторной работе №3 схемам моделирования заданной передаточной функции и матрицам состояния А для методов прямого, параллельного и последовательного программирования определить обратные матрицы в частотной и временной области.
2. С помощью полученных ранее матриц коэффициентов А, В, С и обратных матриц в частотной и временной области для методов прямого, параллельного и последовательного программирования определить произведение матриц CФBU, используя Matlab.
2. Определить  для методов прямого, параллельного и последовательного программирования. Построить графики Y (t).
для методов прямого, параллельного и последовательного программирования. Построить графики Y (t).
Содержание отчета
1. Структурные схемы исследуемой системы, полученные методами прямого, параллельного и последовательного программирования.
2. Расчет обратных матриц в частотной и временной области для методов прямого, параллельного и последовательного программирования.
3. Расчет выходного сигнала для методов прямого, параллельного и последовательного программирования.
4. Графики выходного сигнала для методов прямого, параллельного и последовательного программирования.
Контрольные вопросы
1. Дайте сравнительную характеристику фундаментальных матриц, полученных по методу параллельного программирования и методу прямого программирования.
2. Дайте сравнительную характеристику фундаментальных матриц, полученных по методу параллельного программирования и методу последовательного программирования.
3. Основные свойства фундаментальной матрицы.
4. С помощью какой команды может быть получена обратная матрица в частотной области?
5. С помощью какой команды может быть получена обратная матрица во временной области?
6. Каким образом с помощью Matlab может получено подинтегральное выражение для определения выходного сигнала системы?
7. Каким образом можно записать фундаментальную матрицу в символьном виде?
Лабораторная работа № 5
В пакетах Matlab и Simulink
Цель работы:
1. Изучение возможностей MatLab и Simulink и получение практических навыков по созданию и преобразованию моделей линейных систем;
2. Изучение возможностей MatLab и получение практических навыков по преобразованию структур моделей линейных систем;
Теоретическое обоснование
Лабораторная работа выполняется на основе моделей и индивидуального задания лабораторной работы №3 и дополнительного индивидуального задания по структурам систем.
В практической работе моделирование является более наглядным представлением систем регулирования, чем передаточные функции и уравнения пространства состояния.
Исследования в пакете Simulink позволяют определить влияние изменения параметров системы при уже выбранной структуре. Пакет Control System Tools (CST) обладает более широкими возможностями, чем Simulink, так как позволяет анализировать и исследовать системы во временной и частотных областях с применением методов современной теории управления. Поэтому часто возникают задачи преобразования структурной схемы Simulink в модель CST. В пакете Simulink структурные схемы одной системы могут иметь разные представления. Чтобы из модели Simulink извлечь математическое описание, в структурную схему системы регулирования необходимо добавить к входу входной порт (блок In1), а к выходу – выходной порт (блок Out1), а затем воспользоваться командой linmod.
Линейные модели могут быть представлены в четырех формах:
– передаточная функция (tf);
– нули, полюса и коэффициент усиления (zpk);
– пространство состояния (ss);
– частотные характеристики (frd).
На рис. 5.1 представлена схема, показывающая связи между математическими моделями, представленными в пакете CST.
Из рис. 5.1 видно, что модели, заданные в форме tf, zpk или ss, взаимно преобразуемы. Переход от формы ss к форме tf и zpk задается командами:
w1=ss(A,B,C,D) %Задание модели в форме ss
w2=tf(w1) %Переход от формы ss к форме tf
w3=zpk(w1) %Переход от формы ss к форме zpk
w4=zpk(w2) %Переход от формы tf к форме zpk.
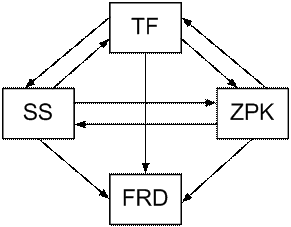
Рис. 5.1. Схема преобразования моделей в пакете CST
Аналогично можно записать команды, преобразующие модель формы zpk к другим формам представления:
w3=zpk(z,p,k) %Задание модели в форме zpk
w2=tf(w3) %Переход от формы zpk к форме tf
w1=ss(w3) %Переход от формы zpk к форме ss.
Модель в форме frd характеризует систему в частотной области. Исходными данными для создания формы frd являются модели, представленные формами: tf, zpk или ss. Для снятия частотных характеристик на вход системы подают синусоидальный сигнал с заданными частотами и команда frd определяет стационарную реакцию на эти возмущения. Для работы с моделью в форме frd в m-файле следует записать следующую программу, из которой следует, что исходная модель задана в форме tf, а тестовые сигналы задаются вектором fred:
w=tf([1,4,3],[1,7,10]); %Исходные данные
fred=[1,2,5,10]; %Входные воздействия
w1=frd(w,fred) %Реакция на входные воздействия.
В пакете CST также имеются команды, позволяющие получать математическое описание сложных систем по их структурным схемам.
Структурная схема последовательного соединения представлена на рис. 5.2.
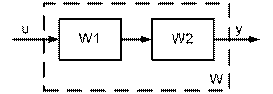
Рис. 5.2. Структурная схема последовательного соединения звеньев
Передаточная функция этого соединения W определяется следующими командами:
w=series(w1,w2)
или
w=w1*w2.
Параллельное соединение звеньев показано на рис. 5.3. Передаточная функция W этой структуры включает следующие команды:
w=parallel(w1,w2),
или
w=w2+w1.

Рис. 5.3. Структурная схема параллельного соединения
При охвате звена W 1обратной связью структура системы принимает вид (рис. 5.4).
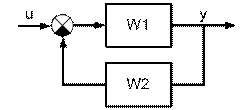
Рис. 5.4. Структурная схема замкнутой системы регулирования
Передаточная функция замкнутой системы определяется выражением: w=feedback(w1,w2).
При положительной обратной связи команда определения W изменяется: w=feedback(w1,w2,+1).
Два звена могут иметь разные входы (горизонтальной конкатенации) – рис. 5.5.

Рис. 5.5. Структурная схема горизонтальной конкатенации
Выходная величина для горизонтальной конкатенации определяется выражением
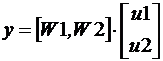 .
.
Передаточная функция, соответствующая структуре рис. 5.5, определяется командой:
w=[w1,w2].
Если два звена имеют общий вход, но разные выходы, то такое соединение образует вертикальную конкатенацию (рис. 5.6).
Выходная величина для вертикальной конкатенации определяется:
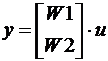 ,
,
а в пакете CST этому соединению соответствует команда:
w=[w1,w2].
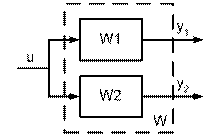
Рис. 5.6. Структурная схема вертикальной конкатенации
При описании моделей систем регулирования в пространстве состояния возникает необходимость компактного описания в соединении блоков, представленных на рис. 5.7.
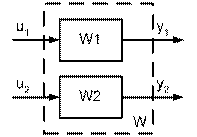
Рис. 5.7. Структурная схема результирующей (агрегативной) модели
Математическая запись структурной схемы рис. 5.7 соответствует формированию диагональной матрицы
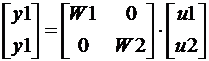 .
.
В пакете CST этому преобразованию соответствует команда:
w=append(w1,w2).
Описание работы
Работу выполняют по заданному индивидуальному варианту лабораторных работ 3, 4.
На рис. 5.8 структурная схема системы (mod05_1) представлена передаточной функцией 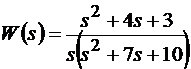 .
.
Структурная схема системы (mod05_2), представленная на рис. 5.9, выполнена методом прямого программирования исходной системы.
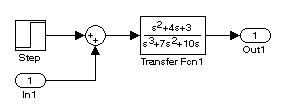
Рис. 5.8. Модель mod05_1
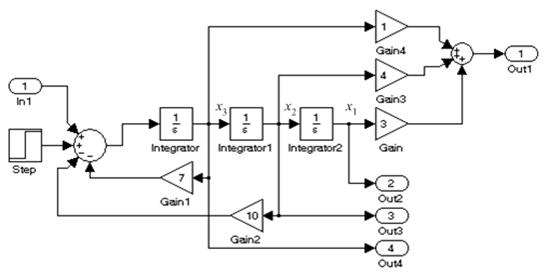
Рис. 5.9. Модель системы, составленная методом прямого программирования
По данной структурной схеме можно определить модель системы.
[A,B,C,D]=linmod('mod05_2'); %Определение матриц системы по модели
%в Simulink
w=ss(A,B,C,D) %Представление матриц в командном окне
figure(1) %MATLAB с выводом фазовых координат
bode(w(1,1)) %Построение ЛАЧХ.
w1=tf(w) %Переход от формы ss к форме tf
w2=zpk(w1) %Переход от формы ss к форме zpk
w3=zpk(w2) %Переход от формы tf к форме zpk.
Амплитудно-частотные и фазо-частотные характеристики модели, составленной методом прямого программирования, представлены на рис. 5.10.
На рис. 5.11 представлена схема моделирования системы (mod05_3) методом параллельного программирования с обозначенными выходными фазовыми координатами x 1, x 2 и x 3, которым соответствуют выходные блоки Out2, Out3 и Out4.
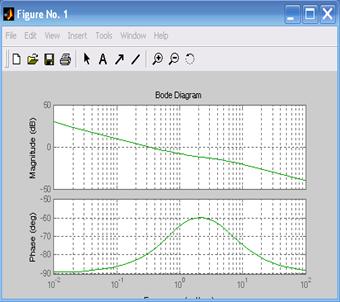
Рис. 5.10. Амплитудно-частотные и фазо-частотные характеристики системы
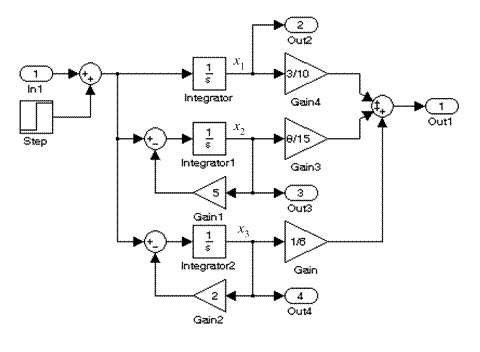
Рис. 5.11. Модель системы, составленная методом параллельного программирования
[A,B,C,D]=linmod('mod05_3'); %Определение матриц системы по модели в
%Simulink
w1=ss(A,B,C,D) %Представление матриц в командном окне
fred=[1,2,5,10]; %Входные воздействия
w4=frd(w1,fred) %Реакция на входные воздействия
figure(2) %с выводом фазовых координат
bode(w(1,1),w1(1,1),w4(1,1)),grid %Построение ЛАЧХ w и w1
figure(3) %Построение переходных функций h и h1
step(w(1,1),w1(1,1)),grid %по координатам выхода и входа.
На рис. 5.12 представлены амплитудно-частотные и фазо-частотные характеристики системы, смоделированной методом параллельного программирования. Дополнительные блоки Out вводят ограничения на выбор базиса и поэтому матрицы A, B, C и D, полученные по первой и по второй схемам разные, хотя они и описывают процессы в одной системе регулирования. В то же время характеристики (частотные и переходные) обеих моделей системы, характеризующие связь выхода с входом, одинаковы, так как они не зависят от выбора базиса. График переходной функции представлен на рис. 5.13.
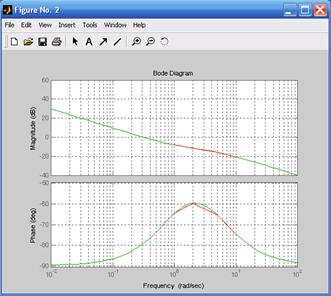
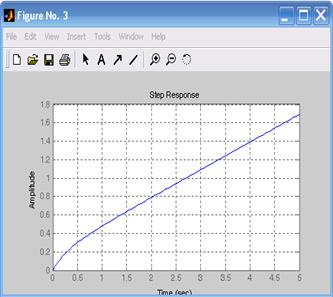
Рис. 5.12. АЧХ и ФЧХ систем Рис. 5.13. Переходные функции систем
(рис. 5.9, 5.11) (рис. 5.9, 5.11)
На рис. 5.14 представлена схема моделирования системы (mod05_4) методом последовательного программирования.
Амплитудно-фазовые и фазо-частотные характеристики моделей mod05_2, mod05_3, mod05_4 представлены на рис. 5.15.
[A,B,C,D]=linmod('mod05_4'); %Определение матрицы системы по модели
%в Simulink
w2=ss(A,B,C,D) %Представление матриц в командном окне
%MATLAB
figure(4) %MATLAB с выводом фазовых координат
bode(w(1,1),w1(1,1),w2(1,1)) %ЛАЧХ mod05_2, mod05_3, mod05_4
[a,b]=ss2tf(A,B,C,D) %Определение полиномов числителя
% и знаменателя.
w1=canon(w,'modal') %Определение модели в модальной форме.
Командой canon определена математическая модель системы в модальной форме. Матрицы A, B, C, полученные командами linmod и canon, отличаются, что объясняется особенностями представления математической модели. В модальной модели все фазовые координаты не воздействуют друг от друга и матрица A имеет диагональный вид. Поэтому выходной сигнал по каждой координате определяется произведением соответствующих компонент матриц C и B. Матрицы C и B,полученные командами linmod и canon, могут и не совпадать, но обязательно должно совпадать их произведение.
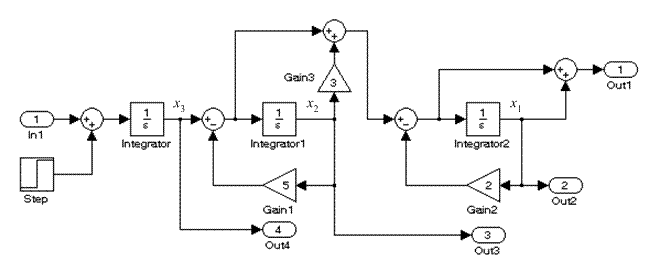 Рис. 5.14. Модель системы, составленная методом последовательного программирования
Рис. 5.14. Модель системы, составленная методом последовательного программирования
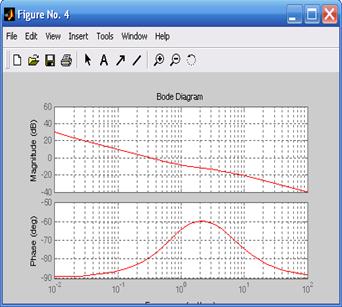
Рис. 5.15. Амплитудно-частотные и фазо-частотные характеристики систем (рис. 5.9, 5.11, 5.14)
На рис. 5.16 представлена структурная схема системы управления, которую необходимо упростить. Структурная схема и передаточные функции звеньев соответствуют индивидуальному заданию.
Сначала необходимо выделить типовые участки, содержащие соединения звеньев (последовательные, параллельные, с обратной связью) для вычисления передаточных функций участков с помощью команд Matlab.
w34=parallel(w3,w4)
w25=feedback(w2,w5).
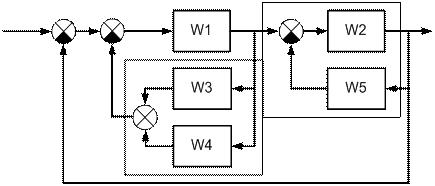
Рис. 5.16. Структурная схема системы управления
Далее для упрощения структуры необходимо заменить каждый типовой участок звеньев одним звеном с рассчитанной передаточной функцией (рис. 5.17 – 5.19) и повторить процедуру расчета.

Рис. 5.17. Упрощение структурной схемы системы управления
w134=feedback(w1,w34)

Рис. 5.18. Упрощение структурной схемы системы управления
w13425=series(w134,w25)

Рис. 5.19. Упрощение структурной схемы системы управления
w=feedback(w13425,1)
Figure(5)
Step(w),grid
Figure(6)
Bode(w),grid.
График переходной функции представлен на рис. 5.20. Графики ЛАЧХ и ЛФЧХ рассматриваемой системы представлен на рис. 5.21.
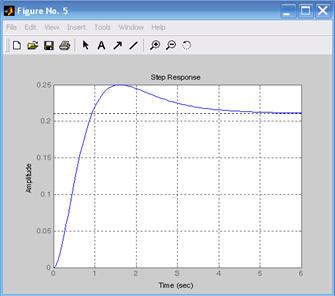
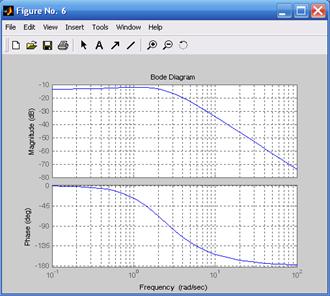
Рис. 5.20. Переходная функция Рис. 5.21. Амплитудно-частотная и
исходной системы фазо-частотная характеристики
Задание
1. По заданной передаточной функции (ЛР №3) методом прямого программирования составить схему моделирования, определить размерность вектора фазовых координат и ввести в структурную схему необходимое количество входных и выходных портов. Сохранить схему.
2. Определить по сохраненной схеме матрицы коэффициентов A, B, C и D. Построить частотные характеристики. Осуществить преобразование модели ss в модели tf, zpk, frd.
3. Повторить пункты 1 и 2 для исходной передаточной функции, составив схему моделирования системы методом параллельного программирования.
4. Повторить пункт 1 и 2 для исходной передаточной функции, составив схему моделирования системы методом последовательного программирования.
5. Построить переходные функции схем моделирования для методов прямого, параллельного и последовательного программирования.
6. Согласно варианту индивидуального задания на структурную схему, определить передаточную функцию системы.
7. Построить переходную функцию и частотные характеристики системы.
Содержание отчета
1. Структурные схемы исследуемой системы, полученные методом прямого параллельного и последовательного программирования с указанием портов входа и выхода системы регулирования.
2. Преобразованные модели систем.
3. Передаточная функция системы, полученная по ее структурной схеме.
4. Переходная функция и частотные характеристики системы, заданной структурной схемой.
Контрольные вопросы
1. Чем объяснить то, что матрицы коэффициентов математической модели системы, реализованные методами прямого, параллельного и последовательного программирования, отличаются друг от друга?
2. Как определить переходную функцию, связывающую заданный выход системы с её входом?
3. Какие исходные данные требуются для формирования модели в форме tf?
4. Какие исходные данные требуются для формирования модели в форме zpk?
5. Какие исходные данные требуются для формирования модели в форме ss?
6. Как сформировать выходные сигналы модели, заданной в форме frd?
7. Как записать модель в форме ss если исходные данные заданы в форме tf?
8. Как записать модель в форме ss если исходные данные заданы в форме zpk?
9. Какой командой определяется последовательное соединение звеньев?
10. Какой командой определяется параллельное соединение звеньев?
11. Какой командой определяется соединение звеньев, образующих горизонтальную конкатенацию?
12. Какой командой определяется соединение звеньев, образующих вертикальную конкатенацию?
13. Как определить передаточную функцию замкнутой системы (обратная связь отрицательная)?
14. Как определить передаточную функцию замкнутой системы (обратная связь положительная)?
15. Как, используя матрицы A, B, C, D представить структурную схему системы?
Лабораторная работа № 6
Figure(5),margin(h3),grid
Figure(6),margin(h4),grid
h10=feedback(h1,1) %Определение передаточных
h20=feedback(h2,1) %функций замкнутых систем
h30=feedback(h3,1)
h40=feedback(h4,1)
figure(7) %Переходные характеристики замкнутых систем
Step(h10,h20,h30,h40,10),grid.
Так как передаточные функции h 1, h 2, h 3 и h 4 отличаются только коэффициентом усиления, то логарифмическая фазовая частотная характеристика будет у них общая (рис. 6.2). Переходные характеристики, иллюстрирующие динамику поведения системы, показаны на рис. 6.3.
Команда margin определяет запасы устойчивости по амплитуде и фазе, а команда step строит переходные характеристики.
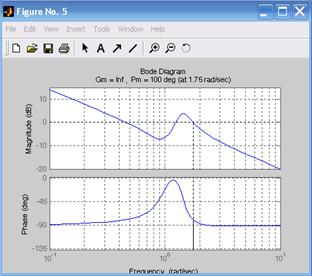
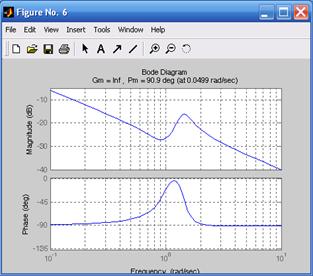
На рис. 6.4 приведены ЛАЧХ и ЛФЧХ исследуемой системы и указаны запасы по амплитуде и по фазе. При этом для k 1 = 100 (рис. 6.4а) запас устойчивости по фазе составляет 89,6° на частоте 100с–1, для k 2 = 10 (рис. 6.4б) запас устойчивости по фазе составляет 89,6° на частоте 10,1с–1, для k 3 = 1 (рис. 6.4в) запас устойчивости по фазе составляет 100° на частоте 1,75с–1, для k 4 = 0,1 (рис. 6.4г) запас устойчивости по фазе составляет 90,9° на частоте 0,050с–1. Так как ЛФЧХ не пересекает значение j = –180°, то запас по амплитуде не определяют.
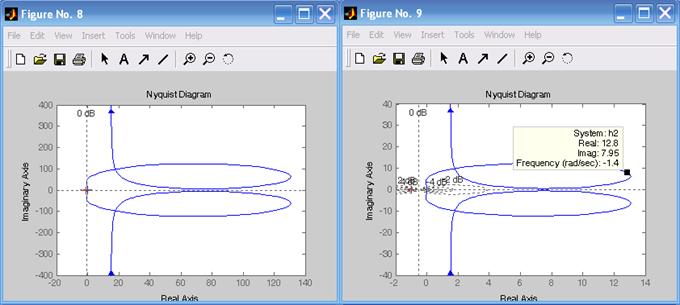
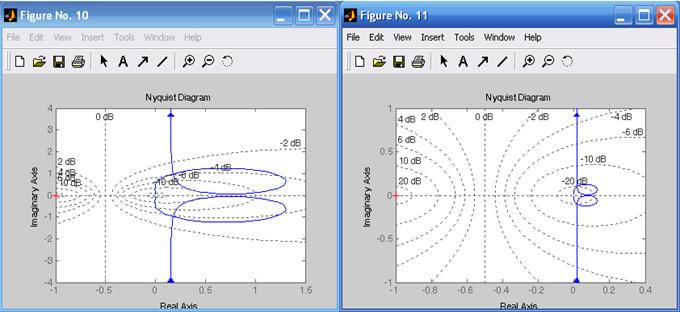
Для рассмотрения устойчивости системы по критерию Найквиста строят АФХ. Так как АФХ разомкнутых систем не охватывает точку (–1, j0), то системы устойчивы в замкнутом состоянии (рис. 6.5).
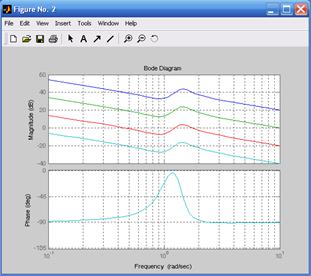
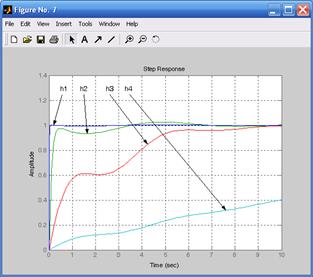
Рис. 6.2. ЛАЧХ и ЛФЧХ Рис. 6.3. Переходные характеристики
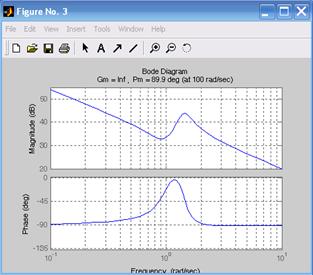
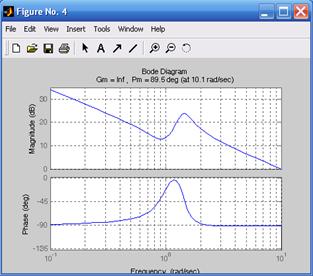
а) б)
в) г)
Рис. 6.4. ЛАЧХ и ЛФЧХ, соответствующие передаточным функциям h 1, h 2, h 3, h 4
а) б)
в) г)
Рис. 6.5. АФХ, соответствующие передаточным функциям h 1, h 2, h 3, h 4
Figure(8), nyquist(h1),grid
Figure(9), nyquist(h2),grid
Лабораторная работа № 7
Figure(5)
plot(t,(yu2+yv2),t,(yu1+yv1),t,(yu3+yv3)),grid.
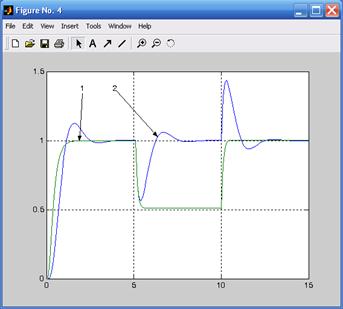
1 – разомкнутая система; 2 – замкнутая система с интегральным законом управления
Рис. 7.7. Переходные характеристики замкнутой системы с И-регулятором
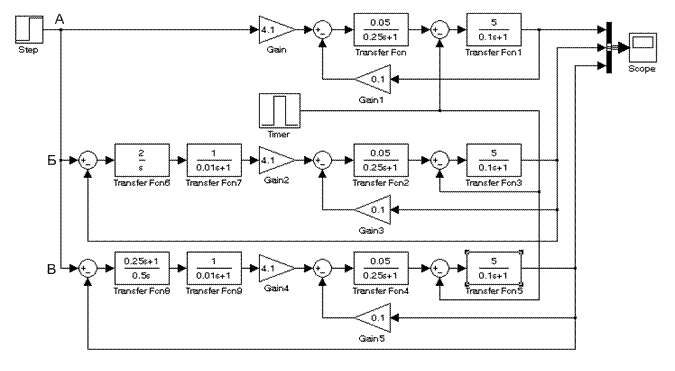
А – разомкнутая система, Б – система с И-регулятором, В – система с ПИ-регулятором
Рис. 7.8. Структурные схемы разомкнутой и замкнутых систем
Результаты моделирования систем в пакете CST приведены на рис. 7.9.
ПИ-регулятор улучшает качество переходных процессов (кривая 3).
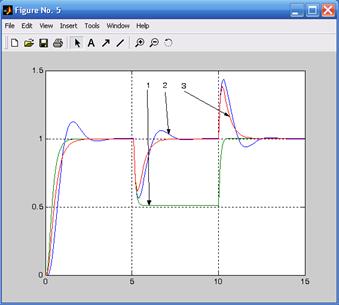
1 – разомкнутая система; 2 – замкнутая система с И-регулятором;
3 – замкнутая система с ПИ-регулятором
Рис. 7.9. Переходные характеристики замкнутой системы с И- и ПИ-регуляторами
Передаточная функция ПИД-регулятора представляет собой параллельное соединение усилительного, интегрирующего и дифференцирующего звеньев.
Структурная схема с ПИД-регулятором представлена на рис. 7.10. Результаты моделирования систем представлены на рис. 7.11.
W3=tf([1,4,1],[1.2,0.3,0]) %Передаточная функция регулятора
W4=tf(1,[0.01,1]) %Передаточная функция усилителя мощности
H1f=feedback(W3*W4*H1,1) %Передаточная функция замкнутой
%системы по управлению
lsim(H1f,u,t); %Реакция замкнутой системы на
[yu4,t,x]=lsim(H1f,u,t); %произвольный сигнал по управлению
H2f=feedback(H2, W3*W4*4.1*W1) %Передаточная функция замкнутой
%системы по возмущению
lsim(H2f,u,t); %Реакция замкнутой системы на
[yv4,t,x]=lsim(H2f,Td,t); %произвольный сигнал по возмущению
Figure(6)
plot(t,(yu2+yv2),t,(yu1+yv1),t,(yu4+yv4),t,(yu3+yv3)),grid.
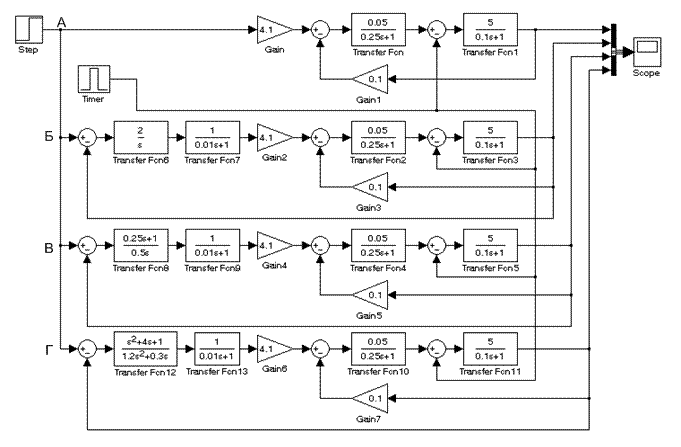 А – разомкнутая система, Б – система с И-регулятором,
А – разомкнутая система, Б – система с И-регулятором,
В – система с ПИ-регулятором, Г - система с ПИД-регулятором
Рис. 7.10. Структурные схемы разомкнутой и замкнутых систем
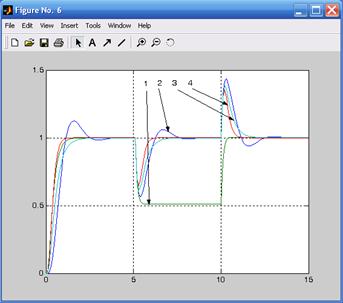
1 – разомкнутая система; 2 – замкнутая система с И-регулятором;
3 – замкнутая сист



 (4.1)
(4.1) ,
,
 дает s X (s) − X (0) = AX (s). Откуда X (s) [ I s − A ] = X (0) или X (s) = [ I s – A ]-1 X (0), где I – единичная матрица.
дает s X (s) − X (0) = AX (s). Откуда X (s) [ I s − A ] = X (0) или X (s) = [ I s – A ]-1 X (0), где I – единичная матрица.  где каждому начальному условию
где каждому начальному условию  соответствует только одно решение дифференциального уравнения, образует N -мерное векторное пространство. Среди множества решений всегда может быть выбрано n линейно независимых. Матрица X (t)[ n ´ n ], столбцами которой являются n линейно независимых решений системы, называется фундаментальной матрицей этой системы дифференциальных уравнений.
соответствует только одно решение дифференциального уравнения, образует N -мерное векторное пространство. Среди множества решений всегда может быть выбрано n линейно независимых. Матрица X (t)[ n ´ n ], столбцами которой являются n линейно независимых решений системы, называется фундаментальной матрицей этой системы дифференциальных уравнений. (4.2)
(4.2) (4.3)
(4.3)
 (4.4)
(4.4)
 C = [3 4 1], D = 0.
C = [3 4 1], D = 0. (4.5)
(4.5) (4.6)
(4.6) (4.7)
(4.7)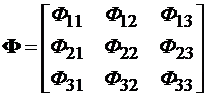 .
.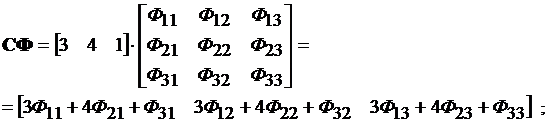
 СФВU = [3 Ф 13 + 4 Ф 23 + Ф 33]×[1] = [3 Ф 13 + 4 Ф 23 + Ф 33] =
СФВU = [3 Ф 13 + 4 Ф 23 + Ф 33]×[1] = [3 Ф 13 + 4 Ф 23 + Ф 33] = .
.



 (4.8)
(4.8)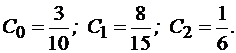 (4.9)
(4.9)
 (4.10)
(4.10)

 D = 0.
D = 0.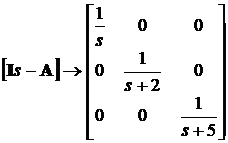





 (4.11)
(4.11)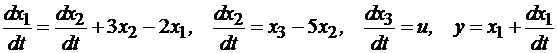


 (4.12)
(4.12)
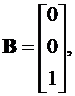 C = [-1 -2 1], D = 0.
C = [-1 -2 1], D = 0.








 для методов прямого, параллельного и последовательного программирования. Построить графики Y (t).
для методов прямого, параллельного и последовательного программирования. Построить графики Y (t).


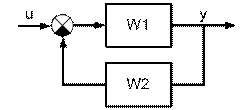

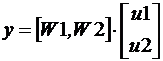 .
.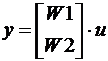 ,
,

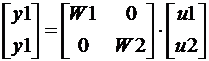 .
.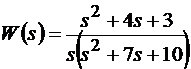 .
.





 Рис. 5.14. Модель системы, составленная методом последовательного программирования
Рис. 5.14. Модель системы, составленная методом последовательного программирования

















 А – разомкнутая система, Б – система с И-регулятором,
А – разомкнутая система, Б – система с И-регулятором,

