Аксиоматическая система Г.Вейля

Эту аксиоматическую систему геометрии Евклида связывают с именем выдающегося немецкого математика первой половины 20 века Германа Вейля (1885-1955 г.г.), который в своей книге «Пространство, время, материя», вышедшей в свет в 1918 году впервые представил новую трактовку евклидова пространства, пологая во главу угла понятие вектора.

Система аксиом использует и описывает шесть основных (неопределяемых) понятий: вектор, точка, сумма векторов, умножение вектора на действительное число, скалярное произведение векторов, откладывание векторов от точки. Роль этих понятий различна, два первых представляют базовые объекты геометрической системы, а четыре последних – базовые отношения между ними.

Итак, даны два множества V, T, а также используется множество действительных чиселR. На множестве V определена бинарная операция со значениями в V, которая называется суммой элементов и обозначается знаком +. Элементы V обозначаются латинскими буквами с верхней чертой, возможно так же использование нижних индексов, например: 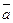или и т.п. Pавенство элементов V означает их совпадение, сами элементы называются векторами.

Первая группа аксиом (аксиомы сложения векторов)

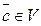I₁ Для любых существует такой, что .

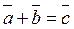I₂ Для любых

I₃ Для любых

I₄ Существует такой, что для любого .

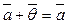I₅ Для любого существует такой, что .

 

Как видим V с операцией + представляет коммутативную группу, которую обычно обозначают (V, +).

 

Определение 1: называется нулевым вектором.

Определение 2: Вектор 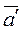, для которого , называется обратным (или противоположным) для . Противоположный для 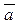вектор обозначают .

Вторая группа аксиом (аксиомы умножения вектора на число)

Существует отображение , которое называют умножением вектора на действительное число. Образ пары называют произведением вектора на действительное число a, его обозначают

Умножение вектора на число обладает свойствами:

II₁ , свойство дистрибутивности относительно сложения векторов.

II₂ , свойство дистрибутивности относительно сложения чисел.

II₃ 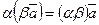, свойство ассоциативности относительно умножения на число.

II₄

 

Структура, состоящая из V и R с операциями сложения на V и умножения элементов V на действительные числа из R, обладающая свойствами, представленными в аксиомах групп I и II, называется векторным пространством над R и обозначается (V, +, ×, R).

 

Третья группа аксиом (аксиомы размерности)

 

Определение 3: Система векторов называется линейно независимой, если равенство имеет место только при условии, что a₁ = a₂ = ….= a_n = 0.

Если найдутся a₁, a₂,…., a_n, не все одновременно равные нулю, такие, что , то система называется линейно зависимой или короче зависимой системой векторов.

III₁ В V существуют три линейно независимых вектора и .

 

 

III₂ Любые четыре вектора из V линейно зависимы.

Аксиомы первых трех групп вводят понятие трехмерного векторного пространства над R, которое обозначают V₃ (R). Всякая система трех линейно независимых векторов этого пространства называется базисом

V₃ (R).

Четвертая группа аксиом (аксиомы скалярного произведения)

 

Существует отображение V´V→ R, называемое операцией скалярного умножения векторов из V. Скалярное умножение векторов и обозначается в виде × , оно обладает следующими свойствами:

IV₁ Для любых , Î V × = × , иначе говоря, скалярное произведение векторов коммутативно.

IV₂ Для любых , и Î V × (b + g ) = b × + g × . Это называют свойством линейности скалярного произведения.

IV₃ Для любого вектора ¹ × > 0.Если = , то × = 0

Определение 4: , как арифметический корень из числа × , называют модулем или длиной вектора .

Определение 5: Число j, косинус которого равен называют углом между векторами и .

Определение 6: Векторы и называют ортогональными, если j =

Это значит, что = 0, что возможно лишь тогда, когда

× =0.

(V,+, ×R), на котором определено скалярное умножение векторов, удовлетворяющее четвертой группе аксиом, называется евклидовым векторным пространством.

Пятая группа аксиом (аксиомы откладывания векторов в Т)

 

Аксиомы этой группы задают отображение Т´Т®V, которое и называют откладыванием вектора от точки в множестве точек Т. Если паре точек

(А, В) как элементу Т´Т соответствует вектор , то мы говорим, что от точки А отложен вектор , причем упорядоченную пару точек (А, В) называем вектором и обозначаем , при этом точку А называют началом, а точку В концом вектора .

V₁ При фиксированной точке А отображение Т´Т®V взаимно однозначно (а потому его можно рассматривать как отображение Т®V).

V ₂ для любых трех точек А,В и С

Множество точек Т, для которого определено отображение Т´Т®V, удовлетворяющее аксиомам V₁ и V₂, при условии, что (V,+,× R) евклидово векторное пространство, называется евклидовым пространством. При условии выполнения для векторного пространства аксиом размерности группы III, Т – трехмерное евклидово пространство.

Аксиоматическая теория, представляющая систему следствий аксиом перечисленных выше групп, называют евклидовой геометрией (трехмерного пространства).

Для математика достоинства векторного определения геометрической системы Евклида несомненны и заключены не только и нестолько, как заявляют многие, в простоте исходных понятий, но в первую очередь в большой общности самих этих понятий, незначительная трансформация которых легко приводит нас к другим геометрическим системам. Иначе говоря, оно заключено, прежде всего, во всеобщности основных исходных понятий. Кроме того, алгебраизация метода обеспечивает алгоритмизацию всей теории.

При всем при том, с точки зрения педагогических целей обучения геометрии в школе, которые, естественно, выступают на первое место, не говоря уже об оторванности исходных понятий от наглядных представлений ученика, алгоритмизация мышления сковывает, если не препятствует, развитию логического мышления учащихся, которое формируется путем большого числа упражнений на материале, имеющем богатую материальную базу.

Таким образом, построение систематического школьного курса геометрии на векторной основе может нанести больше вреда чем пользы не только в деле общего развития ребенка, но и с точки зрения общего математического образования выпускника средней школы.