Оценка точности эмпирической формулы (99)

 

	0,075	0,225	0,1	0,6	0,75
	77,64		65,38	57,84	52,18
	-0,64	1,0	-0,38	0,16	-0,18

 

Сумма квадратов отклонений равна .

 

Вопросы для контроля.

 

1. Какие методы используются для определения параметров эмпирической функции?

2. Покажите последовательность вычислений параметров аппроксимирующ- их функций по методу трех выбранных точек.

3. По каким данным определяются координаты трех выбранных точек?

4. Откуда появляются погрешности при определении параметров функций по методу трех выбранных точек?

5. На чем базируется метод средних определения параметров эмпирических функций?

6. Сколько нормальных уравнений необходимо записать для аппроксимации 10 опытных точек?

7. Минимально на сколько групп будет разбита система 10 начальных уравнений для аппроксимирующей функции в виде квадратичной функции?

8. Как повысить точность определения параметров эмпирической функции по методу средних?

9. Какой критерий принимается для оценки правильности подбора параметров аппроксимирующей функции по методу средних?

10. Каков принцип составления системы нормальных уравнений по точечному методу наименьших квадратов?

 

8. ПРОВЕРКА АДЕКВАТНОСТИ ЭМПИРИЧЕСКИХ ФОРМУЛ

 

После того как уравнение, описывающее опытные данные, получено, приступают к его анализу. При этом решают две основные задачи: оценивают значимость коэффициентов и проверяют адекватность математической модели, т.е. степень соответствия теоретических и опытных данных.

В предыдущих разделах точность эмпирических формул оценивалась по величине разности между опытными и теоретическими значениями функции

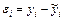, (166)

т.е. по величине абсолютной погрешности аппроксимацию.

Статистическими характеристиками погрешностей эксперимента и погрешностей аппроксимации являются соответственно дисперсия воспроизводимости опытов и дисперсия адекватности математической модели .

Для повышения надежности эксперимента опыты, обычно, повторяют несколько раз или дублируют. При равномерном числе экспериментов каждый из запланированных опытов повторяют одинаковое число раз, т.е. имеется серий, в каждой из которых ставится опытов.

При наличии повторяющихся опытов построение математической модели ведут по средним арифметическим значениям функции , рассчитанным для каждой -той серии опытов

; = 1… ; = 1… . (167)

Величины дисперсии воспроизводимости рассчитывают по выражению

; , (168)

где

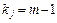, , (169)

и адекватности

 

; , (170)

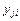где – число серий опытов; – число параллельных опытов в серии; – дисперсия – той серии опытов; – опытное значение функции в – том и – той серии; - вычисленное значение функции; 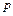– число значимых коэффициентов математической модели; 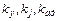– число степеней свободы соответствующих дисперсий.

Прежде чем суммировать дисперсии по выражению (169), необходимо проверить гипотезу о статистической однородности опытов по критерию Кохрена, определив его расчетное значение

. (170)

Расчетное значение сравнивается с табличным 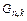, приводимым в справочниках. Рекомендуется брать значение 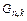, соответствующее уровню значимости = 0,05. Число степеней свободы равно .

Если выполняется условие

, (171)

то полагают, что опыты воспроизводимы (статистически однородны). Если 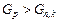, необходимо попытаться добиться воспроизводимости устранением причин нестабильности, а также использованием более точных методов и средств измерений. Значения 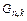для уровня значимости α = 0,05 приведены в таблице 32.

Для оценки значимости коэффициентов математической модели

, (172)

которое в матричной записи имеет вид

, (173)

Таблица 32

Таблица значений критерия Кохрена (уровень значимости )

	0,999	0,975	0,939	0,906	0,877	0,853	0,833	0,816
	0,967	0,871	0,793	0,746	0,707	0,677	0,653	0,633
	0,907	0,768	0,684	0,629	0,590	0,560	0,637	0,518
	0,841	0,684	0,593	0,544	0,507	0,478	0,456	0,439
	0,781	0,616	0,532	0,480	0,445	0,418	0,398	0,382
	0,727	0,561	0,480	0,431	0,397	0,373	0,354	0,338
	0,680	0,516	0,438	0,391	0,360	0,336	0,319	0,304
	0,639	0,478	0,403	0,358	0,329	0,307	0,290	0,277
	0,602	0,445	0,373	0,331	0,303	0,282	0,267	0,254
	0,541	0,392	0,326	0,288	0,262	0,244	0,230	0,219
	0,471	0,335	0,276	0,242	0,220	0,203	0,191	0,182
	0,389	0,271	0,221	0,192	0,174	0,160	0,150	0,142

где 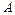- вектор-столбец искомых коэффициентов , ,…, 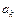; - матрица базисных функций с элементами , ,…, ,…, 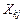; - транспонированная матрица; 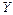- вектор-столбец величин с элементами ; - ковариационная матрица (матрица погрешностей) с элементами. Ее диагональные элементы используются для оценки надежности вычисления коэффициентов , ,…, 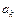математической модели.

Вычисляем дисперсии коэффициентов

, (174)

где – диагональные элементы матрицы погрешности уравнения (173).

Значение коэффициента считается надежным, если выполняется условие

, (175)

где 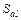– среднеквадратическое отклонение величины , равное корню квадратному из дисперсии ; – коэффициент Стьюдента; – число степеней свободы дисперсии воспроизводимости ; – доверительная вероятность.

Если условие не выполняется, то незначимые коэффициенты из уравнения (172) исключаются, = 0.

Величины для доверительной вероятности = 0,95 приведены в таблице 33.

 

Таблица 33

Фрагмент таблицы Стьюдента. Значения случайной величины для доверительной вероятности = 0,95

											∞
	12,71	4,30	3,18	2,78	2,57	2,45	2,31	2,32	2,13	2,09	1,96

 

Приведем выражения для диагональных элементов матрицы погрешностей , соответствующей простейшим математическим моделям. Следует иметь в виду, что элементы матрицы 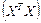равны соответствующим коэффициентам нормальной системы уравнений типа (93). В общем виде матрица погрешностей находится из решения матричного уравнения

, (176)

где – единичная матрица.

Для линейной модели

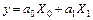(177)

уравнение (176) запишется в виде

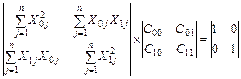. (178)

Откуда при 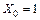, , получим

; . (179)

Для модели

(180)

значение коэффициента 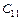равно

. (181)

Если матрица базисных функций (X) (93) обладает свойствами ортогональности

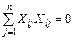; ≠ l, (182)

то недиагональные элементы матрицы 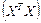равны нулю, что дает простые выражения для диагональных элементов матрицы погрешностей, соответствующей модели (172),

; = 0… . (182)

Для математических моделей с числом коэффициентов больше двух, для которых матрицы базисных функций не обладают свойствами ортогональности, диагональные элементы матрицы погрешностей определяют численными методами.

Если среди коэффициентов оказались незначимые, то их исключают из математической модели. Затем находят новые оценки для оставшихся коэффициентов модели, не содержащей членов с незначимыми коэффициентами.

После оценки значимости коэффициентов математической модели приступают к проверке ее адекватности. Для этого вычисляют по формуле (170) дисперсию адекватности и сравнивают ее с дисперсией воспроизводимости (168).

Если окажется, что дисперсия адекватности (погрешности аппроксимации) меньше дисперсии воспроизводимости (погрешностей опытов), то гипотеза об адекватности математической модели считается справедливой и полученное уравнение может быть рекомендовано для описания опытных данных.

Если больше , то проводят статистическую проверку гипотезы об адекватности математической модели. Для этого вычисляют расчетное значение критерия Фишера.

. (183)

Расчетное значение критерия сравнивают с табличным значением критерия Фишера при числе степеней свободы и .

Если выполняется условие

, (184)

то гипотеза об адекватности математической модели принимается. В противном случае приходится искать другую, более точную, математическую модель.

Значения критерия Фишера приведены в таблице 34.

– степень свободы меньшей дисперсии.

 

Таблица 34

Значения случайной величины , распределенной по закону Фишера, при уровне значимости = 0,05

	– степень свободы большой дисперсии
										∞
	10,13	9,28	9,01	8,88	8,78	8,71	8,66	8,62	8,58	8,54	8,53
	6,61	5,41	5,05	4,88	4,74	4,64	4,56	4,50	4,44	4,38	4,36
	5,12	3,86	3,48	3,29	3,13	3,02	2,93	2,86	2,80	2,73	2,71
	4,49	3,24	2,85	2,66	2,49	2,37	2,28	2,20	2,13	2,04	2,01
	4,17	2,92	2,53	2,34	2,16	2,04	1,93	1,84	1,76	1,66	1,62
	4,03	2,79	2,40	2,20	2,02	1,9	1,78	1,69	1,60	1,48	1,44
	3,89	2,65	2,26	2,05	1,87	1,74	1,62	1,52	1,42	1,26	1,19
∞	3,84	2,60	2,21	2,01	1,83	1,69	1,57	1,46	1,35	1,17	1,00

 

Когда опыты проводятся без дублирования = 1, дисперсию воспроизводимости вычислить невозможно. В этом случае вычисляют остаточную дисперсию

(185)

и ее значение используют для оценки значимости коэффициентов модели вместо дисперсии воспроизводимости в выражении (174).

Затем проводят оценку информативной ценности модели с помощью критерия Фишера. Для этого вычисляют значения остаточной дисперсии линейной модели и дисперсии относительно среднего арифметического

. (186)

Вычисляют расчетное значение критерия Фишера

. (187)

Величина показывает, во сколько раз линейное уравнение описывает результаты эксперимента лучше, чем простое среднее арифметическое , взятое по всем опытам.

Расчетное значение критерия Фишера сравнивают с табличным при числе степеней свободы , .

Если , то линейная модель не дает большего эффекта, чем модель нулевого порядка = . Если , то ищут модель второй степени. Вычисляют для нее остаточную дисперсию и составляют отношение

, (188)

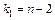Затем снова производится сравнение вычисленного значения критерия с табличным при степенях свободы и .

Если , то линейную модель можно считать пригодной.

Если , то необходимо аналогичным образом проверить, пригодна ли модель второй степени, используя модель третьей степени, и т.д.

П р и м е р 18. Испытания жесткости рамы ходового устройства валочно-пакетирующей машины ЛП-19А проводились методом тензометрирования. Сигнал от тензодатчика, наклеенного на стальную балку, усиливался и подавался на осциллограф, с помощью которого записывался на фотоленту. Перед испытаниями тензодатчики тарировались.

Используя результаты тарировки, приведенные в таблицу 35, определить уравнение тарировочного графика.

 

Таблица 35