Понятие матрицы. Виды матриц

Глава 1

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

Понятие матрицы. Виды матриц

Определение 1.1.1. Матрицей размера m n (m,n N) называется совокупность mn чисел, заданных в виде прямоугольной таблицы, состоящей из m строк и n столбцов

 

(1.1.1)

 

Если число строк в таблице не совпадает с числом столбцов, т.е. 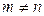, то матрица называется прямоугольной. Матрица, у которой число строк равно числу столбцов (m=n), называется квадратной порядка n.

Числа из таблицы (1.1.1) будем называть элементами матрицы. Элемент, стоящий на пересечении i -й строки и j -го столбца матрицы A, обозначается 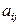. Условимся, что все элементы рассматриваемых нами матриц – действительные числа; будем называть такие матрицы действительными.

Матрицы обозначаются прописными латинскими буквами, а их элементы соответствующими строчными. Для обозначения матрицы (1.1.1) употребляется также запись: 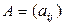, где ; , или A , когда хотят указать размер матрицы. Для квадратных матриц n -го порядка вместо A будем писать .

Пример 1.1.1. Рассмотрим матрицы

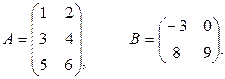
Матрица А – прямоугольная матрица размера 3 2 с элементами: . Матрица B – квадратная 2-го порядка, ее элементы: .

Простейшим соотношением между матрицами является их равенство.

Определение 1.1.2. Две матрицы и называются равными, если они одинаковых размеров, и их соответствующие элементы равны, т. е. ; .

Определение 1.1.3. Диагональ квадратной матрицы, идущая от левого верхнего к правому нижнему углу (составленная из элементов ) называется главной, а диагональ, идущая от верхнего правого к нижнему левому углу () – побочной.

Определение 1.1.4. Квадратную матрицу ; , у которой все элементы, расположенные вне главной диагонали, равны нулю, т. е. , , будем называть диагональной. Она имеет вид

(1.1.2)

В частности, если в матрице (1.1.2) все диагональные элементы равны единице, то такую матрицу называют единичной и обозначают E.

Определение 1.1.5. Матрица O произвольных размеров, у которой все элементы равны нулю, называется нулевой.

Определение 1.1.6. Квадратная матрица 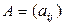; называется треугольной, если все элементы матрицы, расположенные под главной диагональю (над главной диагональю) равны нулю, т. е. при i >j ( при i < j),

(1.1.3)

Первую из этих матриц называют верхней треугольной, а вторую – нижней треугольной.

Замечание 1.1.1. Диагональные матрицы являются частным случаем как верхней треугольной, так и нижней треугольной матриц.

Определение 1.1.7. Матрица произвольного размера

(1.1.4)

называется трапециевидной.

Определение 1.1.8. Прямоугольные матрицы размера m 1 (1 n) называются столбцевыми (строчными) матрицами.

Часто удобно рассматривать матрицу как совокупность строк или столбцов. Например, матрицу (1.1.1) можно представить как строчную матрицу размера 1 n, где каждый элемент – столбец высоты m:

(1.1.5)

или в виде столбцевой матрицы размера m 1, где каждый элемент – строка длиной n:

(1.1.6)

 

 

Операции над матрицами и их свойства

I. Сложение матриц

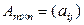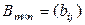Определение 1.2.1. Суммой двух матриц и называется матрица 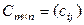такая, что

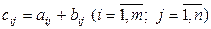, (1.2.1)

т.е. каждый элемент матрицы С равен сумме соответствующих элементов матриц А и В.

Сумма матриц А и В обозначается A+B.

Пример 1.2.1.

Дано

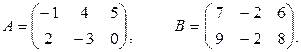
Найти А+В.

Решение.

A+B=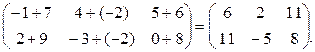

 

Пример 1.2.2.

Дано

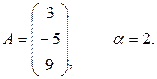
Найти .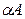

Решение.

 

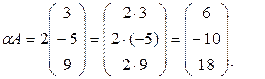
Определение 1.2.3. Матрицу –A= (–1)A будем называть противоположной по отношению к матрице A.

Следствие 1.2.1. Разность матриц А и В определяется как сумма матриц А и (–В):

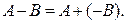
Пример 1.2.3. Найти разность А–В для матриц из примера 1.2.1.

Решение.

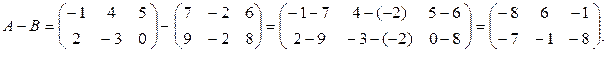
Свойства операций сложения и умножения на число:

1. 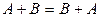(коммутативность сложения).

2. 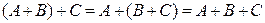(ассоциативность сложения).

3. .

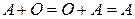4. .

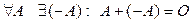5. ,

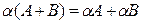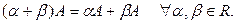
6. .

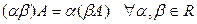7. .

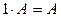Данные свойства представляются очевидными, так как сложение матриц и умножение их на число сводится к сложению и, соответственно, умножению чисел, а для чисел свойства 1–7 справедливы.

 

III. Произведение матриц

Операция умножения вводится только для тех пар матриц, у которых число столбцов первой матрицы совпадает с количеством строк второй.

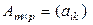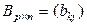Определение 1.2.4. Произведением матриц и называется матрица 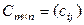такая, что

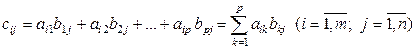, (1.2.3)

т.е. каждый элемент 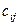матрицы С, расположенный в i -й строке и j -м столбце, равен сумме произведений элементов i -й строки матрицы A на соответствующие элементы j -го столбца матрицы B.

Произведение матриц А и В обозначается A·B.

Замечание 1.2.1. Матрица-произведение состоит из стольких строк, сколько их в первом сомножителе, и из стольких столбцов, сколько их во втором.

Пример 1.2.4.

Дано

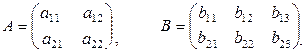
Найти A·B.

Решение.

Для пары матриц A, B операция умножения определена, так как число столбцов матрицы А совпадает с количеством строк матрицы B, причем 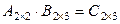. Используя формулу (1.2.3), найдем:

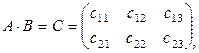
где

 

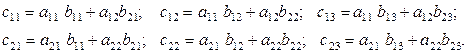
Пример 1.2.5.

Дано

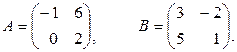
Найти A·B и B·A.

Решение.

Матрицы А и В – квадратные 2-го порядка, следовательно, произведения A·B и B·A определены и будут являться также квадратными матрицами 2-го порядка:

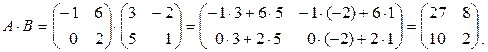
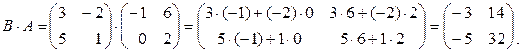
Замечание 1.2.2. Произведение матриц B·A из примера 1.2.4 не определено, так как количество столбцов матрицы B не равно количеству строк матрицы А.

Определение 1.2.5. Целой положительной степенью 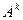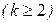квадратной матрицы А называется произведение k -матриц, каждая из которых равна A.

Очевидно, что порядок матриц 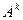и А одинаковый.

Пример 1.2.6.

Дано

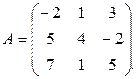
Найти .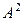

Решение.

 

 

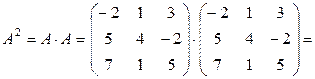
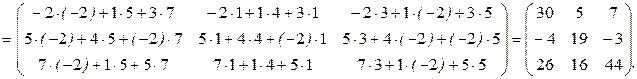
Свойства операции умножения матриц:

1. 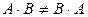(некоммутативность умножения).

2. 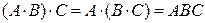(ассоциативность умножения).

3. 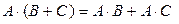(левосторонняя дистрибутивность умножения

относительно сложения).

4. 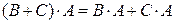(правосторонняя дистрибутивность умножения относительно сложения).

Свойства 1– 4 выполняются для произвольных матриц А, В и С, однако, предполагается, что матрицы имеют размеры, обеспечивающие возможность их перемножения и сложения.

Замечание 1.2.3. В ряде случаев может выполняться 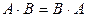, тогда матрицы A и B называются перестановочными или коммутирующими.

Замечание 1.2.4. Единичная матрица является перестановочной с любой квадратной матрицей того же порядка, т. е.

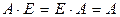. (1.2.4)

Некоммутативность произведения непосредственно следует из формулы (1.2.3), примеров 1.2.4, 1.2.5 и замечания 1.2.2.

Докажем свойство 2.

Дано

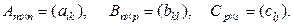
Доказать (A·B)·C=A∙(B·C).

Доказательство.

Введем обозначения:

.

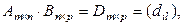
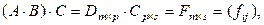
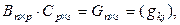
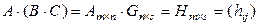Как мы видим, соответствующие произведения матриц слева и справа определены и результат произведений – матрицы F и H имеют одинаковый размер. Покажем, что соответствующие элементы этих матриц равны.

Используя формулу (1.2.3), получим:

,

.

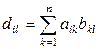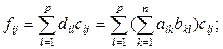
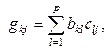
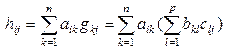Элементы 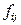и 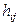отличаются лишь порядком суммирования. Однако, так как суммирования по индексам k и l происходят независимо друг от друга, то порядок их выполнения безразличен. Таким образом, из определения 1.1.2 следует, что F=H.

Свойства 3 и 4 доказываются аналогично свойству 2.

 

IV. Транспонирование матриц

Пусть дана матрица .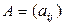

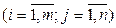Определение 1.2.6. Матрица 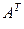, полученная из матрицы А заменой каждой ее строки столбцом с тем же номером, называется транспонированной по отношению к А.

Таким образом, если

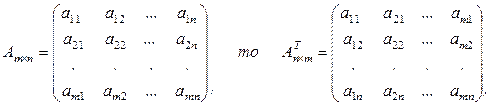(1.2.5)

т.е. .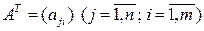

Переход от матрицы А к 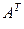называется транспонированием.

Пример 1.2.7.

Дано

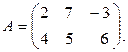
Найти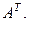

Решение.

 

 

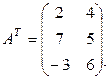
Свойства операции транспонирования:

1. .

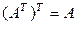2. .

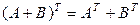3.

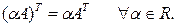
4.

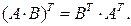
Замечание 1.2.5. Свойства линейности 2 и 3 можно заменить более общим:

.

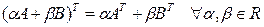Определение 1.2.7. Квадратная матрица 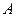называется симметричной, если 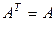и кососимметричной, если .

 

 

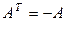Свойства определителей

1. При транспонировании матрицы ее определитель не меняется, т. е.

.

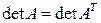Покажем это на примере определителя 2-го порядка:

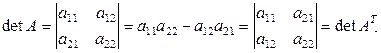
Следствие 1.4.1. Столбцы и строки в определителе равноправны, а именно: всякое утверждение для строк определителя будет верным и для столбцов.

2. Если в определителе поменять две строки (два столбца) местами, то определитель изменит свой знак на противоположный.

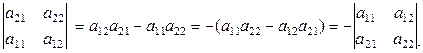
3. Если определитель содержит нулевую строку (столбец), то он равен нулю.

Это непосредственно следует из теоремы 1.3.1, если разложить определитель по нулевой строке.

4. Определитель, содержащий две одинаковых строки (столбца), равен нулю.

Доказательство.

Действительно, пусть 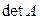имеет две одинаковые строки, т. е. соответствующие элементы i -й и k -й строк 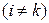равны. Если эти строки поменять местами, то по свойству 2 определитель изменит свой знак на противоположный. На самом же деле, так как переставляются одинаковые строки, определитель не поменяется, т. е.

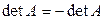. Это равенство возможно, только в том случае, если .

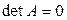5. Если все элементы какой-либо строки (столбца) определителя имеют общий множитель, то его можно выносить за знак определителя.

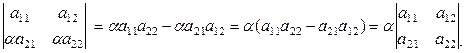
Следствие 1.4.2. Если все элементы одной из строк (одного из столбцов) определителя увеличить в 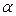(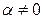) раз, то и сам определитель увеличится в 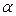раз.

6. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.

Доказательство.

Пусть, например, элементы i -й строки определителя отличаются от соответствующих элементов k -й 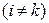одним и тем же множителем 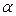. Вынося общий множитель 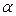из i -й строки за знак определителя, мы получаем две одинаковых строки. По свойству 4 такой определитель равен нулю.

7. Если все элементы i-й строки (j-го столбца) определителя n-го порядка представлены в виде суммы двух слагаемых: 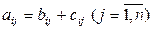, то определитель равен сумме двух определителей, у которых все строки, кроме i-й (все столбцы, кроме j-го), – такие же, как и в данном определителе, а i-я строка (j-й столбец) в первом состоит из элементов 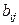, а во втором – из элементов 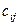, т.е.

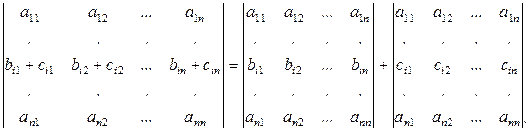
Это свойство называют правилом сложения определителей.

Определение 1.4.1. Говорят, что строка определителя является линейной комбинацией других его строк, если каждый элемент этой строки равен сумме соответствующих элементов других строк, умноженных на некоторые числа.

Аналогичное определение можно сформулировать и для столбцов определителя.

8. Если одна из строк (столбцов) определителя есть линейная комбинация других его строк (столбцов), то определитель равен нулю.

Доказательство.

Пусть, например, i -я строка определителя представляет собой линейную комбинацию k -й и l -й строк, т. е. 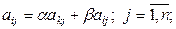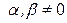. На основании свойства 7 такой определитель равен сумме двух определителей, у которых все строки, кроме i -й такие же, как и в исходном, а i -я строка в первом из них будет состоять из элементов вида 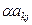,а во втором – из элементов 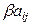. В получившихся определителях содержатся пропорциональные строки, следовательно, по свойству 6, они равны нулю. Таким образом, мы доказали равенство нулю исходного определителя.

9. Величина определителя не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на произвольное число.

Доказательство.

Предположим, что к i -й строке прибавили k -ю, умноженную на некоторое число 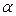. Тогда элементы i -й строки нового определителя имеют вид: 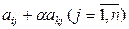. На основании свойства 7, этот определитель равен сумме двух определителей: первый совпадает с исходным, а второй равен нулю, так как содержит две пропорциональные строки.

Замечание 1.4.1. На практике для вычисления определителей удобно применять их свойства. Особенно полезным оказывается использование свойства 9 вместе с теоремой1.3.1 о разложении определителя по элементам строки (столбца). А именно, свойство 9 позволяет преобразовать определитель так, чтобы в любой строке или любом столбце все элементы, кроме одного, заменились нулями. Затем, раскладывая определитель по этой строке (столбцу), мы сводим вычисление определителя n -го порядка к вычислению определителя (n–1) -го порядка.

Пример 1.4.1. Вычислить определитель:

 

 

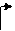
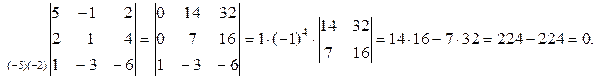
Пример 1.6.1.

Дано

Найти .

Решение.

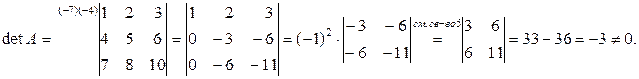
Следовательно, матрица А невырожденная и существует.

Найдем алгебраические дополнения элементов данной матрицы:

Подставляя полученное в формулу (1.6.2), находим

 

Проверка:

.

Замечание 1.6.1. Существует еще один способ нахождения обратной матрицы при помощи элементарных преобразований. Этот способ состоит в следующем: составляется матрица размера , при помощи приписывания к матрице A справа единичной матрицы. Элементарными преобразованиями строк преобразуют полученную матрицу так, чтобы обратить ее левую половину в единичную матрицу. Тогда справа получится матрица .

Пример 1.6.2. Для матрицы из примера 1.6.1 найти обратную матрицу при помощи элементарных преобразований.

Решение.

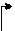
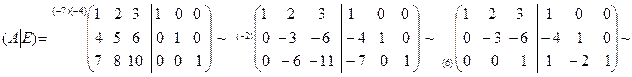
Свойства обратных матриц:

1. .

Непосредственно следует из равенства 1.6.1.

2. .

Доказательство.

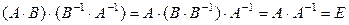. Следовательно, матрицы и 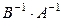обратные по отношению друг к другу, т. е. .

3. .

Доказательство.

Из соотношения 1.6.1: . По свойству 4 операции транспонирования (см. §2) . Следовательно, матрицы и взаимообратные, т. е. .

Определение 1.6.2. Простейшими матричными уравнениями будем называть уравнения следующих трех типов:

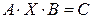, , , (1.6.3)

где 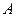, , – некоторые числовые матрицы, а – неизвестная матрица, которую нужно найти.

Под решением матричного уравнения будем понимать матрицу X, которая обращает матричное уравнение в тождество.

Искать решение матричных уравнений будем с помощью обратных матриц в зависимости от типа уравнения следующими тремя способами:

1) Если , то домножая обе части уравнения на слева, получим .

2) Если , то домножая обе части уравнения на справа, получим .

3) Если и , то домножая уравнение 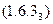на слева и на справа, получим

.

 

Пример 1.6.3. Решить матричные уравнения:

a) b) c)

Решение:

a)Матричное уравнение можно переписать в виде: , где

Получили уравнение вида (1.6. ), решение которого – матрица .

Найдем матрицу :

существует;

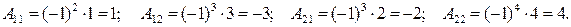
Таким образом,

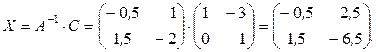
b) Матричное уравнение можно переписать в виде: , где

Получили уравнение вида (1.6. ), решение которого ищется в виде: . Найдем матрицу :

существует;

c) Матричное уравнение можно переписать в виде (1.6. ): , где

Решение данного уравнения ищется в виде: . Найдем матрицы и :

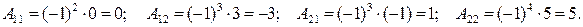
существует;

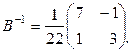
Окончательно, находим

Замечание 1.6.2. В случае, когда 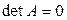и , приведенные способы решений применять нельзя. В этом случае неизвестную матрицу X находят, сводя матричное уравнение к системе линейных уравнений.

Пример 1.6.4. Решить матричное уравнение:

Решение:

Так как , то решать матричное уравнение с помощью обратной матрицы нельзя. Пусть матрица X состоит из элементов , тогда по правилу умножения матриц (1.2.3) имеем:

Используя определение 1.1.2 равенства матриц, составим систему:

Таким образом, матрица X имеет вид: .

Замечание 1.6.3. Более подробно решение систем линейных уравнений мы будем рассматривать в следующей главе.

* Пьер Ф. Саррюс (1798–1858) – французский математик. В 1833 году сформулировал правило для вычисления определителя 3-го порядка, основанное на приписывании к матрице определителя строк или столбцов.

Глава 1

МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

Понятие матрицы. Виды матриц

Определение 1.1.1. Матрицей размера m n (m,n N) называется совокупность mn чисел, заданных в виде прямоугольной таблицы, состоящей из m строк и n столбцов

 

(1.1.1)

 

Если число строк в таблице не совпадает с числом столбцов, т.е. 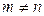, то матрица называется прямоугольной. Матрица, у которой число строк равно числу столбцов (m=n), называется квадратной порядка n.

Числа из таблицы (1.1.1) будем называть элементами матрицы. Элемент, стоящий на пересечении i -й строки и j -го столбца матрицы A, обозначается 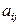. Условимся, что все элементы рассматриваемых нами матриц – действительные числа; будем называть такие матрицы действительными.

Матрицы обозначаются прописными латинскими буквами, а их элементы соответствующими строчными. Для обозначения матрицы (1.1.1) употребляется также запись: 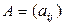, где ; , или A , когда хотят указать размер матрицы. Для квадратных матриц n -го порядка вместо A будем писать .

Пример 1.1.1. Рассмотрим матрицы

Матрица А – прямоугольная матрица размера 3 2 с элементами: . Матрица B – квадратная 2-го порядка, ее элементы: .

Простейшим соотношением между матрицами является их равенство.

Определение 1.1.2. Две матрицы и называются равными, если они одинаковых размеров, и их соответствующие элементы равны, т. е. ; .

Определение 1.1.3. Диагональ квадратной матрицы, идущая от левого верхнего к правому нижнему углу (составленная из элементов ) называется главной, а диагональ, идущая от верхнего правого к нижнему левому углу () – побочной.

Определение 1.1.4. Квадратную матрицу ; , у которой все элементы, расположенные вне главной диагонали, равны нулю, т. е. , , будем называть диагональной. Она имеет вид

(1.1.2)

В частности, если в матрице (1.1.2) все диагональные элементы равны единице, то такую матрицу называют единичной и обозначают E.

Определение 1.1.5. Матрица O произвольных размеров, у которой все элементы равны нулю, называется нулевой.

Определение 1.1.6. Квадратная матрица 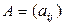; называется треугольной, если все элементы матрицы, расположенные под главной диагональю (над главной диагональю) равны нулю, т. е. при i >j ( при i < j),

(1.1.3)

Первую из этих матриц называют верхней треугольной, а вторую – нижней треугольной.

Замечание 1.1.1. Диагональные матрицы являются частным случаем как верхней треугольной, так и нижней треугольной матриц.

Определение 1.1.7. Матрица произвольного размера

(1.1.4)

называется трапециевидной.

Определение 1.1.8. Прямоугольные матрицы размера m 1 (1 n) называются столбцевыми (строчными) матрицами.

Часто удобно рассматривать матрицу как совокупность строк или столбцов. Например, матрицу (1.1.1) можно представить как строчную матрицу размера 1 n, где каждый элемент – столбец высоты m:

(1.1.5)

или в виде столбцевой матрицы размера m 1, где каждый элемент – строка длиной n:

(1.1.6)