ВВЕДЕНИЕ
Испытания играют очень большую роль в обеспечении необходимого уровня качества изделий на всех стадиях и этапах их жизненного цикла. Особо важную роль испытания играют на стадиях проектирования и серийного производства.
Процесс проектирования боеприпасов (БП) представляет собой сложный интерактивный процесс, состоящий из ряда последовательных этапов. На каждом этапе проектирования одновременно с теоретическими исследованиями и расчетами проводятся разнообразные экспериментальные исследования, то есть испытания.
В процессе проектирования БП должна быть решена задача его оптимального синтеза, то есть должен быть проведен выбор параметров его отдельных элементов таким образом, чтобы все изделие в целом обладало бы заданным качеством.
Сложность математического описания функционирования элементов и всего БП в целом, нестационарность и нелинейность процессов функционирования, случайный характер этих процессов и возмущений, воздействующих на БП, обуславливают существенную сложность задачи и не позволяют создать точную математическую модель и строгого метода оптимального синтеза БП. Поэтому в процессе проектирования решение задачи синтеза распадается на ряд последовательных этапов с характерным для каждого этапа циклом – теория, расчет, эксперимент, анализ.
Расчеты показателей качества на этапе проектирования дают лишь ориентировочное представление о них. Объективное суждение о фактически достигнутом качестве складывается только по результатам испытаний натурных образцов в условиях, близких к реальным.
Испытания не являются каким-то изолированным процессом, а неразрывно связаны с процессом проектирования и являются одной из основных его фаз. Испытания в процессе проектирования выступают в качестве обратных связей на каждом из этапов проектирования БП (рисунок 1).
| Изготовление опытной партии
|
| Испытания составных частей и БП
|
| Изготовление установочной партии
|
| Техническое
проектирование
|
Рисунок 1.
Каждый раз после проведения испытаний осуществляется анализ их результатов, и уточняются математические модели функционирования составных частей и БП в целом, вносятся соответствующие изменения в их схемы и конструкцию. Такую процедуру в технической литературе часто называют опытной отработкой образца.
По мере усложнения БП и повышения предъявляемых к ним тактико-технических требований роль испытаний в процессе проектирования становится все более значительной. Это приводит к тому, что стоимость испытаний по отношению ко всем затратам на проектирование и изготовление БП неуклонно возрастает.
Приведенные соображения свидетельствуют о том, что основным фактором, определяющим стоимость и, что самое главное, сроки разработки проектируемых БП, являются испытания. Поэтому задача сокращения сроков разработки и стоимости, проектируемых БП в основном сводится к задаче оптимального планирования испытаний, т.е. к задаче определения оптимального объема, содержания и последовательности испытаний.
Раздел 1. Виды, методы и задачи испытаний технических изделий
Z- статистика
Двусторонняя КО
 ;
;
 ;
;
 ;
;
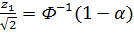 ;
;
 ;
;
 ;
;
 .
.
 ;
;
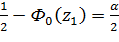 ;
;
 ;
;
 ;
;
 ;
;  .
.
 :
: 

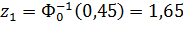

 Но принимается
Но принимается
Односторонняя КО
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;
 ;
;
 ;
;
 .
.
 :
:


 Но отклоняется
Но отклоняется
Вывод: Односторонний критерий является более жестким.

OKO:  ;
;
ДКО:  ,
,  .
.
T- статистика

В силу четности f(x) табулируется не F(t), а функция 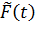
Пример: 
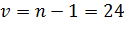
Для ДКО:  ;
;  ;
;
Для ЛКО:  ;
;
Для ПКО:  ;
;
Т.к. 
Для сравнения:
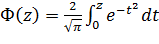 - интеграл ошибок (erf(z)) или функция Лапласа
- интеграл ошибок (erf(z)) или функция Лапласа
Ф(-z) = -Ф(z)
Ф 

F(z) = 
При альтернативе 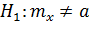 критическая область будет двусторонней:
критическая область будет двусторонней:

Значение критических точек  определяется из уравнений:
определяется из уравнений:
 ;
;
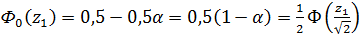 ;
;
 .
.
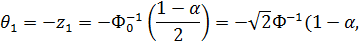
где  есть функции Лапласа
есть функции Лапласа
 ;
;

 .
.
При альтернативе  критическая область будет правосторонней и точка
критическая область будет правосторонней и точка  определится из уравнения:
определится из уравнения:
 ,
,
 .
.
Соответственно для  имеем левостороннюю область и
имеем левостороннюю область и

Пример 












| 
|
 Но принята Но принята
|  Но отклоняется Но отклоняется
|
Вывод: Односторонний критерий является более жестким, чем двусторонний.
Если дисперсия  известна, то используют статистику
известна, то используют статистику
 ,
,
где  - статистическая дисперсия:
- статистическая дисперсия:

Известно:  , где v = n-1
, где v = n-1


Функция квавантилей для t –распределения рассчитана (затабулирована) на основе зависимости:
 ,
,
где 
Поэтому:
 и
и

Пример



 v = 24
v = 24


 Но принимается
Но принимается
| 
 Но отклоняется
Но отклоняется
|
Сравнение средних двух совокупностей
Пусть имеются две выборки объемом  соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних
соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних  и
и  . Требуется проверить гипотезу
. Требуется проверить гипотезу 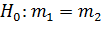 . Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты.
. Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты.
Первый вариант: дисперсии выборок  известны и равны друг другу, а так же
известны и равны друг другу, а так же  Рассмотрим разность
Рассмотрим разность  . Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза
. Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза  верна:
верна:


Выберем в качестве статистики величину
 ; D [
; D [ 
Если  верна, то M [
верна, то M [ 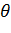 ], и D [
], и D [  , т.е.
, т.е.  и поэтому дальнейшая проверка ведется по общей схеме.
и поэтому дальнейшая проверка ведется по общей схеме.
Второй вариант: выборки малы ( ),
),  неизвестны, то можно полагать (есть основания)
неизвестны, то можно полагать (есть основания)  .
.
Тогда определяют общую (двух выборок) статистическую дисперсию
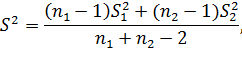
где  – статистические дисперсии выборок.
– статистические дисперсии выборок.
На роль статистики принимают величину

которая подчиняется t - распределению с числом степеней свободы v=  .
.
Дальнейшая проверка ведется по общей схеме.
Третий вариант:  неизвестны и нет оснований полагать их равными, т.е.
неизвестны и нет оснований полагать их равными, т.е.  . Имеем проблему Беренса-Фишера.
. Имеем проблему Беренса-Фишера.
Пример
Вывод: Чем выше уровень доверительной вероятности, тем шире доверительный интервал!
Аналогичным образом можно определить доверительный интервал для дисперсии, если  . Для этого достаточно воспользоваться V-статистикой, имеющей
. Для этого достаточно воспользоваться V-статистикой, имеющей 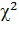 -распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид:
-распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид:
 ,
,
откуда 

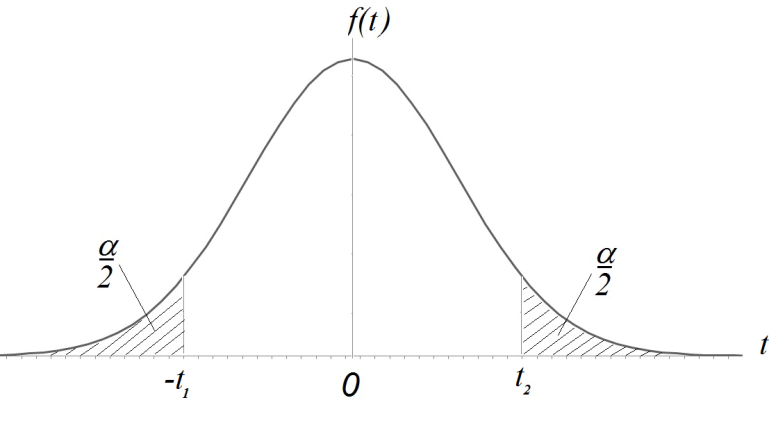
Как видно из рисунка, закон распределения статистики V в отличие от закона распределения статистики T не является симметричным. Поэтому возникает вопрос: как выбрать интервал  , в который величина V =
, в который величина V = 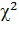 попадает с вероятностью
попадает с вероятностью 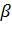 ?
?
Условимся выбирать интервал  так, чтобы вероятности выхода величины V за пределы интервала вправо и влево (заштрихованные площади на рисунке) были одинаковы и равны
так, чтобы вероятности выхода величины V за пределы интервала вправо и влево (заштрихованные площади на рисунке) были одинаковы и равны
 .
.
Чтобы построить интервал  с таким свойством надо воспользоваться таблицей, в которой приведены числа
с таким свойством надо воспользоваться таблицей, в которой приведены числа 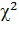 такие, что
такие, что
 .
.
Зафиксировав ν = n-1, находят по таблице два значения 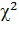 :
:
Одно 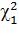 , отвечающие вероятности
, отвечающие вероятности  , и другое
, и другое  , отвечающее вероятности
, отвечающее вероятности  . Очевидно, что интервал
. Очевидно, что интервал 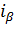 имеет
имеет  своим левым, а
своим левым, а 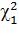 - правым концом.
- правым концом.
Теперь по интервалу  найдем искомый интервал
найдем искомый интервал  для неизвестной дисперсии
для неизвестной дисперсии  с границами
с границами  и
и  , который накрывает точку D с вероятностью
, который накрывает точку D с вероятностью 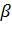 :
:

Для этого убедимся в равносильности неравенств:

 ,
,
Откуда:
 и
и 
Пример:


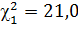

n =13 ν = 12 

Если интегрировать слева направо:



Корреляционным анализом называется совокупность методов статистической обработки результатов испытаний, зависящих от различных одновременно действующих факторов, с целью анализа и оценки существенности влияния данных факторов на отклик.
В отличие от дисперсионного анализа, при проведении которого любые факторы рассматриваются как качественные, в корреляционном анализе могут рассматриваться как качественные, так и количественные факторы, хотя предпочтение отдается последним.
Сущность корреляционного анализа заключается в установлении стохастической зависимости между откликом и факторами и в определении существенности влияния факторов на отклик, степени тесноты стохастической связи между ними. Смысл понятия «корреляционная зависимость» удобнее рассматривать для случая одномерных фактора и отклика, образующих систему случайных величин (X,Y).
Прежде всего, необходимо отметить, что корреляционная зависимость является разновидностью стохастической зависимости и уже по этой причине не является жесткой, функциональной. При изучении такой зависимости между компонентами системы (X,Y) возможны 2 различных подхода к формированию исходных предположений. Первый заключается в том, что определяемые значения переменной X задаются, т.е. не являются случайными. Тогда каждому фиксированному значению х соответствуют некоторые генеральные распределения Y/х с математическим ожиданием M[Y/x] и дисперсией D[Y/x], а наблюдаемые на опыте значения у рассматриваются как выборочные значения из этой генеральной совокупности. Зависимость M[Y/x] = φу(х) называется, как уже отмечалось, регрессией Y на Х.
Второй подход к формированию исходных предположений состоит в том, что реализации случайной переменной Х, т.е. значения х, не задаются, а генерируются датчиком нормально распределенных чисел. А так как одно из основных допущений корреляционного анализа, как и дисперсионного, заключается в предположении о том, что участвующие в анализе переменные распределены нормально, это следует признать, что в этом случае реализации Х и Y, наблюдаемые на опыте, будут представлять собою выборку из двумерного нормального распределения. При таком варианте исходных предположений компоненты системы (X,Y) становятся как бы полностью «равноправными». Вследствие чего необходимо вести речь о регрессии Y на Х, но и о регрессии Х на Y, т.е. о зависимости:
M [Х/у] = φх(у)
Поэтому приходим к выводу, что корреляционная зависимость, как разновидность стохастической, может быть представлена двумя уравнениями регрессии - φу(х) и φх(у).
Зависимости φу(х) и φх(у) могут быть как линейными, так и не линейными. Соответственно различают линейный и нелинейный корреляционный анализ. Обычно предполагается линейный характер этих регрессий. В этом предположении заключается второе из основных допущений корреляционного анализа (первое предполагает нормальность распределения компонент Х и Y). Оно гласит: регрессия имеет линейный или близкий к линейному характер.
Поэтому обычно полагают:
φу(х) = β0 + βх (12.1)
φх(у) = γ0 + γy
Такая связь или корреляция называется парной. Если с увеличением одной из компонент условное среднее другой также возрастает, то корреляция называется положительной, в противном случае – отрицательной.
Для определения коэффициентов в уравнениях (12.1) используются диаграммы или корреляционные поля. Каждая точка такого поля имеет координаты xi, yi , соответствующие значениям переменных в i -том опыте. Обработка опытных данных ведется методом наименьших квадратов. В итоге получают оценку b0 для β0, b для β и т.д.
Эта процедура называется параметризацией уравнений (12.1).
Определение характера зависимостей φу(х) и φх(у), т.е. установление формы стохастической связи между компонентами Х и Y, является одной из основных задач корреляционного анализа. Вторая основная задача заключается в определении существенности этой связи, т.е. существенности взаимовлияния компонент Х и Y. С решением этих задач связанны основные процедуры корреляционного анализа, рассмотренные в следующем параграфе.
В заключение отметим основные виды корреляционного анализа. Они различаются:
-по количеству факторов – однофакторный, многофакторный (множественный);
-по количеству откликов – одномерный, многомерный (векторный);
-по форме стохастической связи – линейный, нелинейный.
Однофакторный корреляционный анализ.
Основные этапы и соответствующие им процедуры корреляционного анализа рассмотрим на примере однофакторного одномерного анализа, позволяющего изучить взаимовлияние двух случайных компонент – фактора Х и отклика Y.
Первым этапом корреляционного анализа является установление наличия стохастической связи между компонентами Х и Y. Для этого используются рассмотренные ранее процедуры дисперсионного анализа. Если по итогам дисперсионного анализа делается вывод о наличии стохастической связи, то переходят ко второму этапу.
Вторым этапом является установление формы стохастической связи, т.е. решение вопроса о том, линейна она или нелинейна. Решение данной задачи может проводиться качественными и количественными методами.
Качественные методы опираются на анализ поля корреляции, а количественные – на методы построения кривой, наилучшим образом аппроксимирующей результаты наблюдений. В случае использования количественных методов выдвигается гипотеза о типе кривой, а затем осуществляется её параметризация, например, с помощью метода наименьших квадратов. В полном объеме эта процедура рассматривается на заключительных этапах регрессионного анализа.
Третьим, заключительным этапом корреляционного анализа является определение существенности стохастической связи между фактором и откликом.
Если стохастическая связь между переменными является линейной, то мерой этой связи служит парный коэффициент корреляции, определяемый выражением:
rхy =Кху/ϬхϬу =М[(X-mх)(Y-mу)] /ϬхϬу (12.2)
Если исследуемые переменные связаны функциональной зависимостью, то rхy=±1, а в случае их независимости rхy=0.
На практике используется оценка парного коэффициента корреляции, определяемая по опытным данным:
 (12.3)
(12.3)
Значимость этой оценки проверяется на основе гипотез:
H0: rхy = 0
H1: rхy ≠ 0
В случае большой выборки оценка  распределена по нормальному закону с параметрами:
распределена по нормальному закону с параметрами:
M [  ] = 0
] = 0
D [  ] = (1- rхy2)2 /n
] = (1- rхy2)2 /n
Поэтому основная гипотеза может быть проверена с использованием Z – статистики, при формировании которой следует использовать оценку дисперсии D [  ], т.е.
], т.е. 
Если выборка не является большой, то используется статистика
 , (12.4)
, (12.4)
которая подчиняется t – распределению с числом степеней свободы υ = n-2.
В случае отклонения основной гипотезы выборочный коэффициент корреляции признается значимым с выбранным уровнем значимости. Он характеризует степень приближения стохастической зависимости между переменными к линейной. Для количественной оценки нелинейности используется так называемый коэффициент детерминации ɳху, который определяется как rхy2. Этот коэффициент позволяет ответить на вопрос о том, каково качество описания зависимости с помощью уравнения регрессии. Очевидно, чем теснее наблюдения примыкают к линии регрессии, тем лучше она описывает соответствующую зависимость переменных и с большей надежностью может быть применена для оценивания значений отклика по заданным значениям фактора.
Можно показать, что rхy2 равен отношению межуровневой дисперсии к общей дисперсии отклика, откуда следует, что коэффициент детерминации характеризует долю так называемой объясненной регрессией дисперсии в общей величине дисперсии. Чем теснее наблюдения примыкают к линии регрессии, тем эта доля выше. Например, если rхy =0,9, то ɳху = rхy2 = 0,81. Это значит, что 81% общей дисперсии (общей для среднего значения отклика) определяется уравнением регрессии, т.е. корреляционная связь между откликом и фактором вполне удовлетворительно может быть представлена линейным уравнением, т.к. доля нелинейности сравнительно невелика.
Проверкой значимости оценки rхy завершаются основные процедуры корреляционного анализа.
Лекция 7. Регрессионный анализ и планирование эксперимента.
1). Назначение и сущность регрессионного анализа. Классификация по видам.
2). Планирование эксперимента. Как метод реализации процедуры РА. Критерии оптимальности планов.
Назначение и сущность регрессионного анализа. Классификация по видам.
Регрессионным анализом называется один из видов статистического анализа, представляющий собою совокупность методов обработки результатов испытаний, зависящих от различных одновременно действующих случайных факторов различной природы, с целью построения уравнения регрессии в интересах исследования стохастической взаимосвязи между откликом и факторами.
Таким образом, исходная предпосылка заключается в том, что между случайным откликом Y и случайным вектором факторов X существует стохастическая зависимость вида 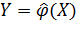 , где
, где  в общем случае может быть как случайной, так и неслучайной функцией случайных аргументов, вид которой неизвестен. Если бы была известна зависимость закона распределения Y от вектора X, то она позволила бы провести всесторонний анализ стохастической взаимосвязи Y и X. Такой путь решения задачи в принципе возможен, но как свидетельствует опыт исследований, не всегда целесообразен. В практике испытаний гораздо чаще используется другой вариант решения, идея которого заключается в том, чтобы установить зависимость какой-либо числовой характеристики Y от возможных значений компонент вектора X в виде неслучайной функции неслучайных аргументов. В регрессионном анализе в качестве такой числовой характеристики используется условное математическое ожидание отклика Y, определяемое при условии, что компоненты вектора X приняли определенные значения:
в общем случае может быть как случайной, так и неслучайной функцией случайных аргументов, вид которой неизвестен. Если бы была известна зависимость закона распределения Y от вектора X, то она позволила бы провести всесторонний анализ стохастической взаимосвязи Y и X. Такой путь решения задачи в принципе возможен, но как свидетельствует опыт исследований, не всегда целесообразен. В практике испытаний гораздо чаще используется другой вариант решения, идея которого заключается в том, чтобы установить зависимость какой-либо числовой характеристики Y от возможных значений компонент вектора X в виде неслучайной функции неслучайных аргументов. В регрессионном анализе в качестве такой числовой характеристики используется условное математическое ожидание отклика Y, определяемое при условии, что компоненты вектора X приняли определенные значения: 
 ….,
….,  ….
….
Следовательно, в РА используется зависимость вида:
 (13.1)
(13.1)
где:  ,
,
 - неслучайная функция неслучайных аргументов.
- неслучайная функция неслучайных аргументов.
Эта зависимость предназначена для того, чтобы приближенно представлять истинную стохастическую взаимосвязь между откликом и факторами, т.е. она является регрессией отклика на факторы.
Таким образом, в представлении соотношения 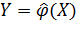 в виде (13.1) заключается сущность РА, а в построении зависимости (13.1) по результатам испытаний – его цель.
в виде (13.1) заключается сущность РА, а в построении зависимости (13.1) по результатам испытаний – его цель.
Различают однофакторный и многофакторный, одномерный и многомерный РА, а по виду зависимости  – линейный и нелинейный.
– линейный и нелинейный.
В линейном РА зависимость (1) представляют в виде полинома:
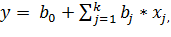
где  - оценка коэффициентов регрессии
- оценка коэффициентов регрессии  (
(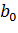 – оценка для
– оценка для  ).
).
В нелинейном РА зависимость (13.1) обычно включает члены, представляющие так называемые эффекты взаимодействия и степенные эффекты, т.е. члены вида
 и т.д.
и т.д.
Активный и пассивный эксперимент.
Исходные понятия ТПЭ: фактор, отклик, план эксперимента.
Отклик Y – однокомпонентный вектор. Фактор X – многокомпонентный вектор столбец вида:
В каждом опыте участвуют все факторы, так что в i -м опыте имеем:
 ;
; 
Всего опытов N, т.е. i = 1, 
Матрицей спектра плана эксперимента называется матрицы вида:
X =  =
= 
 N точек с координатами (
N точек с координатами (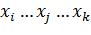 )
)
Совокупность всех точек в пространстве k факторов, отличающихся уровнями хотя бы одного фактора, называется спектром плана эксперимента.
Опыт в i -х условиях может повторяться n раз, что можно представить матрицей дублирования опытов e:
e = 
Матрица спектра совместно с матрицей e дает план эксперимента, совокупность данных, определяющих число, условия и порядок реализации опытов.
ПЭ:
точный, если  задана;
задана;
насыщенный, если N=k (без учёта  )
)
регулярный, если 
Разработка плана эксперимента (ПЭ):
Определение пространства факторов
Выбор стратегии испытания
Полный факторный эксперимент
1. Принятие решений перед планированием эксперимента.
2. Полный факторный эксперимент типа. Его свойства и математическая модель.
Принятие решений перед планированием эксперимента.
Исследование на основе теории планирования эксперимента предполагает использование как формальных, так и не формальных процедур. Последние требуют «Интуитивных решений». Перед планированием эксперимента такие решения должны быть приняты по трем вопросам:
Выбор экспериментальной области факторного пространства, выбор основного уровня факторов и выбор интервала варьирования факторов. При этом предполагается, что сама совокупность исследуемых факторов уже сформирована и цель исследования определена.
Выбор экспериментальной области: ( области определения факторного пространства) прежде всего, означает оценку границ областей определения факторов, т.е. возможных диапазонов изменения каждого из выбранных факторов. При этом обычно учитываются ограничения трех типов.
Первый тип- принципиальные ограничения, которые не могут быть нарушены ни при каких обстоятельствах. Например, если фактор температура, то нижним пределом будет абсолютный нуль.
Второй тип- ограничения, связанные с технико-экономическими соображениями: стоимостью сырья, дефицитностью отдельных компонентов, времени ведения процесса.
Третий тип ограничений, с которыми чаще всего приходится иметь дело, определяется конкретными условиями эксперимента: существующей аппаратурой, технологией, организацией.
На данном этапе рекомендуется тщательный анализ и активное использование всей имеющейся априорной информации о каждом из выбранных факторов.
Выбор основного уровня: Основным (нулевым) уровнем называется такое значение фактора, относительно которого осуществляется варьирование данным фактором в ходе эксперимента.
Выбор основного уровня зависит от цели исследования. Если цель исследования заключается в характере влияния факторов на отклик, то в качестве основного уровня следует выбирать середину диапазона возможных значений каждого фактора:

где  - натуральное значение верхней границы диапазона изменения j -го фактора;
- натуральное значение верхней границы диапазона изменения j -го фактора;
 - натуральное значение нижней границы диапазона изменения j -го фактора;
- натуральное значение нижней границы диапазона изменения j -го фактора;
 - натуральное значение основного (нулевого) уровня j -го фактора.
- натуральное значение основного (нулевого) уровня j -го фактора.
В тех случаях, когда целью эксперимента является поиск оптимальных условий, т.е. условий, при которых отклик достигает оптимального значения, в качестве основного уровня для каждого из факторов выбирают координаты так называемой наилучшей точки:

Это такая точка в k -мерном фактором пространстве, в которой получено наилучшее значение отклика. Если такая точка известна из анализа априорной информации, то полагают:
 т.е.
т.е. 
Если априорные значения координат наилучшей точки неизвестны, то рекомендуется случайным образом выбрать несколько (минимум две) точек в факторном пространстве, поставить в них предварительные опыты и на этой основе определить лучшую из них. Найденная точка называется центром плана.
Выбор интервалов варьирования факторов заключается в том, чтобы для каждого фактора выбрать два уровня, на которых он будет варьироваться в эксперименте. В общем случае уровней может быть больше двух. Мы ограничимся двумя.
Представим себе координатную ось, на которой откладываются натуральные значения j -го фактора:
После выбора основного уровня нам известна точка  . тогда два интересующих нас уровня можно изобразить двумя точками
. тогда два интересующих нас уровня можно изобразить двумя точками  (нижний уровень) и
(нижний уровень) и  (верхний уровень) симметричными относительно основного уровня. Обычно за верхний уровень принимается тот, который соответствует большему значению фактора, хотя это и не обязательно.
(верхний уровень) симметричными относительно основного уровня. Обычно за верхний уровень принимается тот, который соответствует большему значению фактора, хотя это и не обязательно.
Интервалом варьирования факторов называется число, свое для каждого фактора, прибавление которого к основному уровню дает верхний, а вычитание - нижний уровни фактора. Обозначается интервал выравнивания через 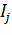 .
.
Для упрощения записи условий эксперимента масштабы по осям выбирают так, чтобы верхний уровень соответствовал «+1», нижний «-1», а основной-нулю. Для факторов с непрерывной областью определения это всегда можно сделать с помощью процедуры кодирования факторов:

Где  -ко
-ко



 ;
; ;
; ;
;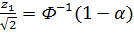 ;
; ;
; ;
; .
. ;
;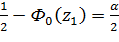 ;
; ;
; ;
; ;
;  .
. :
: 

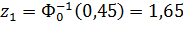

 Но принимается
Но принимается ;
; ;
; ;
; ;
; ;
;
 ;
; ;
; ;
; ;
; .
. :
:

 Но отклоняется
Но отклоняется
 ;
; ,
,  .
.
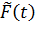

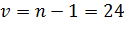
 ;
;  ;
; ;
; ;
;
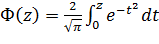 - интеграл ошибок (erf(z)) или функция Лапласа
- интеграл ошибок (erf(z)) или функция Лапласа


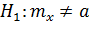 критическая область будет двусторонней:
критическая область будет двусторонней:
 определяется из уравнений:
определяется из уравнений: ;
;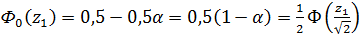 ;
; .
.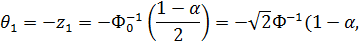
 есть функции Лапласа
есть функции Лапласа ;
;
 .
. критическая область будет правосторонней и точка
критическая область будет правосторонней и точка  определится из уравнения:
определится из уравнения: ,
, .
. имеем левостороннюю область и
имеем левостороннюю область и












 известна, то используют статистику
известна, то используют статистику ,
, - статистическая дисперсия:
- статистическая дисперсия:

 , где v = n-1
, где v = n-1

 ,
,
 и
и


 Но принимается
Но принимается
 Но отклоняется
Но отклоняется
 соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних
соответственно. Предполагается, что они получены из одной и той же генеральной совокупности. В результате обработки опытных данных получены оценки средних  и
и  . Требуется проверить гипотезу
. Требуется проверить гипотезу 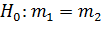 . Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты.
. Решение зависит от имеющихся сведений о дисперсиях. Рассмотрим возможные варианты. известны и равны друг другу, а так же
известны и равны друг другу, а так же  Рассмотрим разность
Рассмотрим разность  . Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза
. Это случайная величина. Определим ее МОЖ и дисперсию, полагая, что гипотеза  верна:
верна:

 ; D [
; D [ 
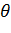 ], и D [
], и D [  , т.е.
, т.е.  и поэтому дальнейшая проверка ведется по общей схеме.
и поэтому дальнейшая проверка ведется по общей схеме. ),
),  неизвестны, то можно полагать (есть основания)
неизвестны, то можно полагать (есть основания)  .
.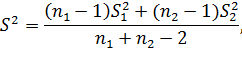
 – статистические дисперсии выборок.
– статистические дисперсии выборок.
 .
. . Имеем проблему Беренса-Фишера.
. Имеем проблему Беренса-Фишера. ;
;


 ;
;





 . Для этого достаточно воспользоваться V-статистикой, имеющей
. Для этого достаточно воспользоваться V-статистикой, имеющей 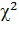 -распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид:
-распределение с ν = n-1 степенями свободы. Как известно, эта статистика имеет вид: ,
,

 , в который величина V =
, в который величина V = 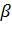 ?
? .
. .
.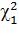 , отвечающие вероятности
, отвечающие вероятности  , и другое
, и другое  , отвечающее вероятности
, отвечающее вероятности  . Очевидно, что интервал
. Очевидно, что интервал 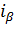 имеет
имеет  для неизвестной дисперсии
для неизвестной дисперсии  с границами
с границами  и
и  , который накрывает точку D с вероятностью
, который накрывает точку D с вероятностью 

 ,
, и
и 


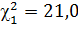






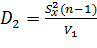
 (12.3)
(12.3) распределена по нормальному закону с параметрами:
распределена по нормальному закону с параметрами:
 , (12.4)
, (12.4)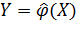 , где
, где  в общем случае может быть как случайной, так и неслучайной функцией случайных аргументов, вид которой неизвестен. Если бы была известна зависимость закона распределения Y от вектора X, то она позволила бы провести всесторонний анализ стохастической взаимосвязи Y и X. Такой путь решения задачи в принципе возможен, но как свидетельствует опыт исследований, не всегда целесообразен. В практике испытаний гораздо чаще используется другой вариант решения, идея которого заключается в том, чтобы установить зависимость какой-либо числовой характеристики Y от возможных значений компонент вектора X в виде неслучайной функции неслучайных аргументов. В регрессионном анализе в качестве такой числовой характеристики используется условное математическое ожидание отклика Y, определяемое при условии, что компоненты вектора X приняли определенные значения:
в общем случае может быть как случайной, так и неслучайной функцией случайных аргументов, вид которой неизвестен. Если бы была известна зависимость закона распределения Y от вектора X, то она позволила бы провести всесторонний анализ стохастической взаимосвязи Y и X. Такой путь решения задачи в принципе возможен, но как свидетельствует опыт исследований, не всегда целесообразен. В практике испытаний гораздо чаще используется другой вариант решения, идея которого заключается в том, чтобы установить зависимость какой-либо числовой характеристики Y от возможных значений компонент вектора X в виде неслучайной функции неслучайных аргументов. В регрессионном анализе в качестве такой числовой характеристики используется условное математическое ожидание отклика Y, определяемое при условии, что компоненты вектора X приняли определенные значения: 
 ….,
….,  ….
…. (13.1)
(13.1) ,
, - неслучайная функция неслучайных аргументов.
- неслучайная функция неслучайных аргументов.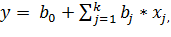
 - оценка коэффициентов регрессии
- оценка коэффициентов регрессии  (
(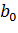 – оценка для
– оценка для  ).
). и т.д.
и т.д. , j=1,
, j=1, 

 ;
; 

 =
= 
 N точек с координатами (
N точек с координатами (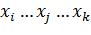 )
)
 задана;
задана; )
)

 - натуральное значение верхней границы диапазона изменения j -го фактора;
- натуральное значение верхней границы диапазона изменения j -го фактора; - натуральное значение нижней границы диапазона изменения j -го фактора;
- натуральное значение нижней границы диапазона изменения j -го фактора; - натуральное значение основного (нулевого) уровня j -го фактора.
- натуральное значение основного (нулевого) уровня j -го фактора.
 т.е.
т.е. 

 . тогда два интересующих нас уровня можно изобразить двумя точками
. тогда два интересующих нас уровня можно изобразить двумя точками  (нижний уровень) и
(нижний уровень) и  (верхний уровень) симметричными относительно основного уровня. Обычно за верхний уровень принимается тот, который соответствует большему значению фактора, хотя это и не обязательно.
(верхний уровень) симметричными относительно основного уровня. Обычно за верхний уровень принимается тот, который соответствует большему значению фактора, хотя это и не обязательно. .
.
 -ко
-ко


