ГЛАВА 2. MATLAB в задачах вычислительной

ГЛАВА 2. MATLAB в задачах вычислительной

Математики

Система MATLAB обладает большими возможностями программирования и комплексной визуализации результатов инженерных расчетов и научных исследований. В этой связи покажем применение богатых возможностей MATLAB в решении задач вычислительной математики. Развитие многих наук привело исследователей к необходимости численного решения различных проблем, т. е. применению численных методов. Численные методы создаются и исследуются высококвалифицированными специалистами – математиками и, как в системе MATLAB, предлагаются для применения в виде готового инструмента. Поэтому задачей данной главы является изложение основных идей численных методов и ознакомление с последовательностью применения численных процессов в современных компьютерных системах

Программы, реализующие какой-либо численный метод, необходимо записывать в М-файл. Если не дать имени М-файлу, то он запишется при выполнении программы в рабочую папку под именем Untitled (Безымянный). Такой ситуации следует избегать для исключения появления множества файлов с неопределенным именем. Рассмотрим решение некоторых важных проблем вычислительной математики.

12.8000 0.3609

23.4000 0.2327

27.2000 0.1473

17.8000 0.1800

16.3000 0.1771

14.9000 0.1658
Варианты заданий

Составить программу вычисления значений функции у_i для значений аргумента х_i. Данные взять из таблицы 2.1.

Таблица 2.1

№ п/п	Функция yi = f(xi)	Задача А	Задача В
a	в	xH	xK	Dx	x1	x2	x3	x4	x5
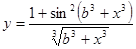
		-	2.5	1.28	3.28	0.4	1.1	2.4	3.6	1.7	3.9
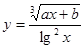
		1.35	0.98	1.14	4.24	0.62	0.35	1.28	3.51	5.21	4.16
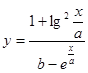
		2.0	0.95	1.25	2.75	0.3	2.2	3.78	4.51	6.58	1.2
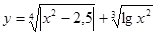
		-	-	1.25	3.25	0.4	1.84	2.71	3.81	4.56	5.62
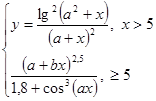
		- 2.5	3.4	3.5	6.5	0.6	2.89	3.54	5.21	6.28	3.48
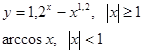
		-	-	0.2	2.2	0.4	0.1	0.9	1.2	1.5	2.3

Продолжение таблицы 2.1

№ п/п	Функция yi = f(xi)	Задача А	Задача В
a	в	xH	xK	Dx	x1	x2	x3	x4	x5
		0.4	0.8	3.2	6.2	0.6	4.48	3.56	2.78	5.28	3.21
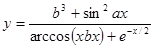
		1.2	0.48	0.7	2.2	0.3	0.25	0.36	0.56	0.94	1.28
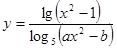
		1.1	0.09	1.2	2.2	0.2	1.21	1.76	2.53	3.48	4.52
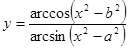
		0.05	0.06	0.2	0.95	0.15	0.15	0.26	0.37	0.48	0.56
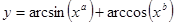
		2.0	3.0	0.11	0.36	0.05	0.08	0.26	0.35	0.41	0.53
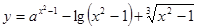
		1.6	-	1.2	3.7	0.5	1.28	1.36	2.47	3.68	4.56
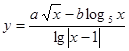
		4.1	2.7	1.2	5.2	0.8	1.9	2.15	2.34	2.73	3.16
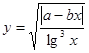
		7.2	4.2	1.81	5.31	0.7	2.4	2.8	3.9	4.7	3.16
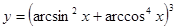
		-	-	0.26	0.66	0.08	0.1	0.35	0.4	0.55	0.6
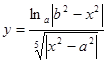
		2.0	1.1	0.08	1.08	0.2	0.1	0.3	0.4	0.45	0.65
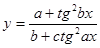
		0.1	0.5	0.15	1.37	0.25	0.2	0.3	0.44	0.6	0.56
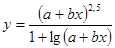
		2.5	4.6	1.1	3.6	0.5	1.2	1.28	1.36	1.46	2.35
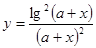
		2.0	-	1.2	4.2	0.6	1.16	1.32	1.47	1.65	1.93
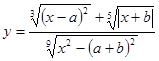
		0.8	0.4	1.23	7.23	1.2	1.88	2.26	3.84	4.55	-6.21
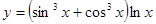
		-	-	0.11	0.36	0.05	0.2	0.3	0.38	0.43	0.57
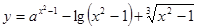
		2.25	-	1.2	2.7	0.3	1.31	1.39	1.44	1.56	1.92
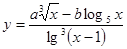
		4.1	2.7	1.5	3.5	0.4	1.9	2.15	2.34	2.74	3.16
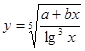
		7.2	1.3	1.56	4.71	0.63	2.4	2.8	3.9	4.7	3.16
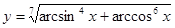
		-	-	0.22	0.92	0.14	0.1	0.35	0.4	0.55	0.6

Продолжение таблицы 2.1

№ п/п	Функция yi = f(xi)	Задача А	Задача В
a	в	xH	xK	Dx	x1	x2	x3	x4	x5
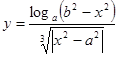
		2.0	4.1	0.77	1.77	0.2	1.24	1.38	2.38	3.21	0.68
		0.1	0.5	0.33	1.23	0.18	0.5	0.36	0.40	0.62	0.78
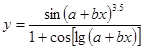
		2.5	4.6	1.15	3.05	0.38	1.2	1.36	1.57	1.93	2.25
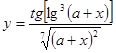
		2.0	-	1.08	1.88	0.16	1.16	1.35	1.48	1.52	1.96
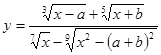
		0.8	0.4	1.42	3.62	0.44	1.6	1.81	2.24	2.65	3.38

 

Решение систем линейных алгебраических уравнений

К решению систем линейных уравнений сводятся многочисленные практические задачи, например различные краевые задачи для обыкновенных дифференциальных уравнений и уравнений в частных производных. Можно с полным основанием утверждать, что данная проблема является одной из самых распространенных и важных задач вычислительной математики.

Пусть задана система п линейных алгебраических уравнений с п неизвестными:

 

. (2.1)

Система уравнений (2.1) в матричной форме представляется следующим образом:

АХ = В, (2.2)

где А – квадратная матрица коэффициентов, размером п ´ п строк и столбцов;

Х – вектор-столбец неизвестных;

В – вектор-столбец правых частей.

В MATLAB имеется обширный арсенал методов решения систем уравнений (2.2). Применяются, в частности, следующие операторы

\	- левое деление;
Ù - 1	- возведение в степень –1;
inv(A)	- обращение матрицы А.
/	- правое деление;
A¢, B¢	– транспонирование матриц

 

 

Выражения

Х	=	A\В
Х	=	А^ - 1* В
Х	=	inv(A) * В
Х	=	В¢/A¢

 

дают решения ряда систем линейных уравнений АХ = В, где А – матрица размером m ´ n, В – матрица размером п ´ к, в частности - столбец. Более сложные случаи решения систем уравнений (2.2) с плохо обусловленной матрицей А рассматривать не будем.

Пример 3.

Решить систему 4-х линейных уравнений:

Протокол программы (в М-файле)

A	=	[1.1161 0.1397 0.1254 0.1490; 0.1582 0.1768 1.1675 0.1871; 0.1968 1.2168 0.2071 0.2271; 0.2368 0.2568 0.2471 1.2671]
B	=	[1.5471; 1.6471; 1.7471; 1.8471];

 

Х1 = A \ B

Эта программа выдает решение заданной системы в виде матрицы-столбца

Х1

=

1.0406 0.9351 0.9870 0.8813

 

Внимание. В М-файле матрица A набирается по строкам, в правой части B – столбец. Элементы B отделяются символом «;» (точка с запятой).Число строк в обеих матрицах должно совпадать.

Операцию «\» называют операцией левого деления (или же умножения слева на обратную матрицу inv(A)). Этой операции эквивалентна функция A\B = mldivide(A,B) (Matrix left division), вызываемая в командном окне.

Х

=

inv(A) * В.

Систему можно также решить, вычисляя обратную матрицу inv(A) и умножая на нее слева вектор (матрицу) правых частей системы В

Решение с помощью оператора «\» эффективнее, чем использование обратной матрицы. Это объясняется тем, что алгоритм решения системы линейных уравнений при помощи оператора «\» определяется структурой матрицы коэффициентов системы. В частности, MATLAB исследует, является ли матрица треугольной, или может быть приведена перестановками строк и столбцов к треугольному виду, симметричная матрица или нет, квадратная или прямоугольная (умеет решать системы с прямоугольными матрицами – переопределенные или недоопределенные). Использовать специальные методы вместо оператора обратного деления «\» следует, если имеется информация об особенных свойствах матрицы системы.

Операция правого деления «/» также имеется в MATLAB, но она решает системы линейных уравнений несколько иного вида Y × A = B и поэтому требует перестановки местами матриц А и В. Выражение В¢/А¢ эквивалентно В¢*inv(A¢) или вызову функции mrdivide(B¢,A¢) - right-matrix division. При правом делении у матриц должно совпадать число столбцов, поэтому в нашем случае берутся транспонированные матрицы В¢, А¢

А¢	=	[1.1161 0.1582 0.1968 0.2368; 0.1397 0.1768 1.2168 0.2568; 0.1254 1.1675 0.2071 0.2471; 0.1490 0.1871 0.2271 1.2671];
В¢	=	[1.5471 1.6471 1.7471 1.8471];

 

Решения, найденные с помощью команд

 

Х2 = В¢* А¢ ^ - 1

Х3 = В¢ * inv (А¢)

Х4= В¢/ А¢,

будут иметь вид вектора-строки.

 

Х1	=	1.0406 0.9351 0.9870 0.8813
Х2	=	1.0406 0.9351 0.9870 0.8813
Х3	=	1.0406 0.9351 0.9870 0.8813

 

Варианты заданий. Решить систему линейных алгебраических уравнений с помощью 4-х операторов. Данные взять из таблицы 2.2.

Таблица 2.2

 

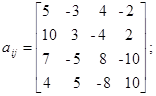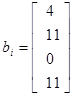
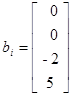
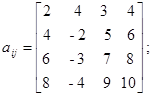
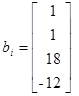
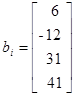
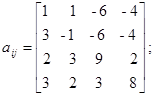
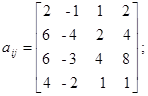
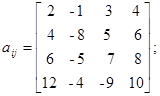
Аппроксимация функций

Одним из распространенных и практически важных случаев связи между аргументом и функцией является задание этой связи в виде некоторой таблицы { x_i; y_i }, например, экспериментальные данные. На практике часто приходится использовать табличные данные для приближенного вычисления у при любом значении аргумента х (из некоторой области). Этой цели служит задача о приближении (аппроксимации) функций: данную функцию f (x) требуется приближенно заменить некоторой функцией g (х) так, чтобы отклонение g (х) от f (x) в заданной области было наименьшим. Функция g (х) при этом называется аппроксимирующей. Если приближение строится на заданном дискретном множестве точек { x_i }, то аппроксимация называется точечной. К ней относятся интерполирование, среднеквадратичное приближение и др. При построении приближения на непрерывном множестве точек (например, на отрезке [ a, b ]) аппроксимация называется непрерывной или интегральной. MATLAB имеет мощные средства точечной и непрерывной аппроксимации с визуализацией результата. Рассмотрим наиболее важную точечную аппроксимацию (обработка экспериментальных данных).

 

Пример 4. Используя линейную и полиномиальную аппроксимации, получить эмпирические формулы для функции у = f (x), заданной в табличном виде:

xi	0.75	1.50	2.25	3.00	3.75
yi	2.50	1.20	1.12	2.25	4.28

Оценить погрешность эмпирических формул.

Протокол программы. В окне команд набираются значения x_i и y_i. Далее выполняется команда построения графика только узловых точек.

>> x = [0.75, 1.50, 2.25, 3.00, 3.75];

>> y = [2.50, 1.20, 1.12, 2.25, 4.28];

>> рlot (x, y, ¢ 0 ¢);

 

 

Появляется окно с символами ¢ 0 ¢ на месте узловых точек (рис. 2.1).

4.5
3.5
3
2.5
2
1.5
0.5
	0.5		1.5		2.5		3.5

 

Рис. 2.1

 

Внимание. Следует помнить, что при полиномиальной аппроксимации максимальная степень полиноме на 1 меньше числа экспериментальных точек!

На панели инструментов окна графика узловых точек в меню Tools исполняем команду Basic Fitting. Появляется окно Основной Монтаж. В этом окне птичкой отмечаются необходимые данные аппроксимации. В частности, можно задать следующие операции:

- показать уравнение аппроксимирующей функции у = g (х);

- выбрать метод подбора: сплайн интерполяции

эрмитовская интерполяция

линейный

квадратные

кубический

…………….

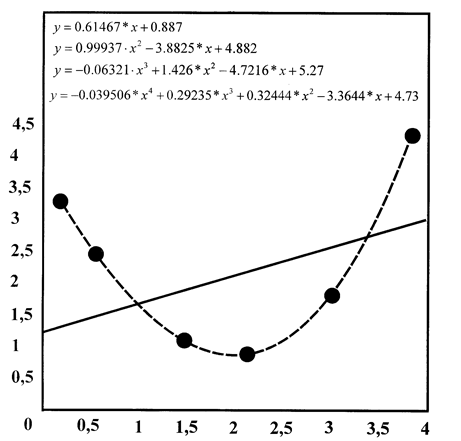
В нашей задаче выбираем линейную и полиномиальную аппроксимации. В окне графика появляются соответствующие графики разноцветом и формулы аппроксимирующих функций (рис. 2.2).

 

Рис. 2.2

 

Чтобы узнать погрешность аппроксимации, надо отметить птичкой параметр График остатка в окне Основной Монтаж, и Показать норму остатков. График погрешностей с нормами можно вынести в отдельное окно, или вместе с графиком и аппроксимирующих функций – суб-график. Норма погрешностей указывает на статистическую оценку среднеквадратической погрешности. Чем она меньше, тем точнее полученная аппроксимирующая функция у = g (х). В нашем примере:

Linear: norm of residuals ( норма погрешности) = 2.1061

Quadratic: norm of residuals = 0.10736

Cubic: norm of residuals = 0.035857

4 th degree: norm of residuals = 9.6305 e -015.

График погрешностей можно выводить в виде диаграмм (зоны), линий (линии) или отдельных точек (фрагменты). Сам график погрешностей представляет собой зависимость разности g (х) - f (x) в условных точках, соединенных прямыми линиями.

Кроме линейной и полиномиальной аппроксимации можно выбрать сплайн- аппроксимацию – когда на каждом интервале приближения используется кубический полином с новыми коэффициентами. В этом случае нельзя получить выражение для аппроксимирующей функции, т. е. такая аппроксимация является неполной. Аналогичными свойствами обладает и Эрмитовая аппроксимация. Она имеет только графическую интерпретацию.

Варианты заданий. Получить эмпирические формулы и оценить их погрешность для функции у = f (x), заданной таблично. Данные взять из таблицы 2.3.

Таблица 2.3

1.	xi	-3	-2	-1
yi	-0.71	-0.01	0.51	0.82	0.88	0.51	0.49
2.	xi	-6.6	-5.38	-3.25	-1.76	2.21	3.6	4.5
yi	2.89	1.41	0.29	-0.41	-0.69	-0.7	1.2
3.	xi
yi	-0.31	0.9	2.11	3.3	4.51	5.73	6.93
4.	xi	-2	-1
yi	7.1	3.9	1.1	0.8	3.1	4.5	5.3
5.	xi	-2	-1	-0.5		1.5		3.5
yi	5.9	2.8	2.1	3.2	6.1	7.6	4.3
6.	xi	-3	-2	-1
yi	3.1	0.9	0.9	2.8	7.1	6.5	4.1
7.	xi
yi	10.0	7.5	5.5	4.0	3.0	2.0	2.24
8.	xi	-2	-1		1.5	2.3	2.6	2.9
yi	4.2	5.6	6.8	7.2	9.4	10.5	11.8
9.	xi	10.0	12.0	13.0	15.0	18.0	20.0	21.0
yi	0.66	0.89	1.24	1.36	1.56	1.76	1.92
10.	xi	22.0	24.0	27.0	30.0	31.0	35.0	40.0
yi	1.24	1.37	1.46	1.26	1.66	1.84	1.99
11.	xi	-7.0	-6.0	-5.0	-4.0	-3.0	-2.0	-1.0
yi	22.6	24.7	25.6	24.6	23.5	21.8	19.3
Продолжение таблицы 2.3
12.	xi	-25.0	-23.0	-21.0	-18.0	-17.2	-15.4	-14.0
yi	0.76	0.74	0.61	0.58	0.84	0.92	1.22
13.	xi	-4.0	-3.0	-2.0	-1.0	0.0	1.0	2.0
yi	1.71	1.56	1.24	1.36	1.78	2.21	4.31
14.	xi	-22.0	-20.0	-18.0	-16.0	-14.0	-12.0	-10.0
yi	-2.26	-1.84	-1.92	-1.76	-1.56	-1.64	-1.34
15.	xi	23.0	24.0	25.0	26.0	27.0	28.0	29.0
yi	1.26	1.37	1.44	1.56	1.15	1.28	1.06
16.	xi	30.0	33.0	35.0	37.0	39.0	41.0	43.0
yi	-2.6	-3.7	-2.5	-4.3	-2.3	-5.6	-1.9
17.	xi	44.0	45.0	46.0	47.0	48.0	49.0	50.0
yi	2.24	3.46	5.36	1.89	1.76	1.54	2.12
18.	xi	52.0	54.0	56.0	58.0	60.0	62.0	64.0
yi	-1.28	-1.33	-1.44	-1.67	-1.77	-2.81	-2.16
19.	xi	2.2	2.6	3.0	3.4	3.8	4.2	4.6
yi	1.88	1.65	1.61	1.73	1.56	1.24	1.99
20.	xi	5.1	5.3	5.5	5.7	5.9	6.1	6.3
yi	-2.8	-3.6	-5.7	-3.4	-1.9	-1.7	-1.5
21.	xi	7.15	7.35	7.55	7.75	7.95	8.15	8.35
yi	-2.2	-3.6	-1.7	-2.8	-1.6	-4.5	-2.2
22.	xi	9.1	9.2	9.3	9.4	9.5	9.6	9.7
yi	1.48	1.16	2.08	1.96	1.81	2.31	5.61
23.	xi	-10.2	-10.1	-10.0	-9.9	-9.8	-9.7	-9.6
yi	-6.5	-7.8	-10.2	-5.4	-4.6	-9.5	-10.3
24.	xi	11.0	14.0	17.0	20.0	23.0	26.0	29.0
yi	1.2	1.6	1.9	1.1	1.16	1.24	1.36
25.	xi	-50.0	-48.0	-46.0	-44.0	-42.0	-40.0	-38.0
yi	1.23	1.32	1.57	1.19	1.16	1.10	2.28
26.	xi	-36.0	-34.0	-32.0	-30.0	-28.0	-26.0	-24.0
yi	1.1	1.3	2.1	1.9	1.7	1.5	1.8
27.	xi	21.0	23.0	24.0	28.0	31.0	32.0	36.0
yi	1.24	1.37	1.56	1.64	1.84	1.26	1.14
28.	xi	10.0	13.0	17.0	22.0	28.0	35.0	43.0
yi	1.21	1.36	1.51	1.84	1.06	1.21	1.36
29.	xi	-1.0	0.0	3.0	5.0	8.0	12.0	15.0
yi	-2.1	-3.6	1.2	-4.3	1.8	2.6	-0.2
30.	xi	-8.0	-7.0	-5.0	-3.0	-1.0	2.0	5.0
yi	1.36	1.88	2.45	-2.1	-10.2	-4.4	1.16

 

 

Уравнений

Многие задачи физики, химии, экологии, механики и других разделов науки и техники при их математическом моделировании сводятся к дифференциальным уравнениям. Поэтому решение дифференциальных уравнений является одной из важнейших математических задач. В вычислительной математике изучаются численные методы решения дифференциальных уравнений, которые особенно эффективны в сочетании с использованием персональных компьютеров.

Среди множества численных методов решения дифференциальных уравнений наиболее простые – это явные одношаговые методы. К ним относятся различные модификации метода Рунге-Кутта.

Постановка задачи:

Требуется найти функцию у = у (х), удовлетворяющую уравнению

(2.3)

и принимающую при х = х ₀ заданное значение у ₀:

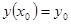. (2.4)

При этом решение необходимо получить в интервале х ₀ £ х £ х _к. Из теории дифференциальных уравнений известно, что решение у (х) задачи Коши (2.3), (2.4) существует, единственно и является гладкой функцией, если правая часть F (x, y) удовлетворяет некоторым условиям гладкости. Численное решение задачи Коши методом Рунге-Кутта 4-го порядка заключается в следующем. На заданном интервале [ х ₀, х _к] выбираются узловые точки. Значение решения в нулевой точке известно у (х ₀) = у ₀. В следующей точке у (х ₁) определяется по формуле

, (2.5)

здесь

(2.6)

т. е. данный вариант метода Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения (2.3). Этот алгоритм реализован в программе ode45. Кроме этой программы MATLAB располагает обширным набором аналогичных программ, позволяющих успешно решать обыкновенные дифференциальные уравнения.

 

Пример 5. Решить задачу Коши

. (2.7)

Точное решение имеет вид

.

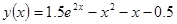Выполним решение данной задачи с помощью программы ode45. Вначале в М-файл записываем правую часть уравнения (2.7), сам М-файл оформляется как файл – функция, даем ему имя F:

function dydx = F(x, y)

dydx = zeros (1,1);

dydx (1) = 2*(x^2+y(1));

Для численного решения задачи Коши в окне команд набираются следующие операторы.

Протокол программы.

>>[X Y] = ode45 (@ F, [0 1], [1]);

% Дескриптор @ обеспечивает связь с файлом – функцией правой части

% [0 1] – интервал на котором необходимо получить решение

% [1] – начальное значение решения

>> рlot (X,Y);

>> % Построение графика численного решения задачи Коши (2.7)

>> hold on; gtext (¢ y (x) ¢)

% Команда позволяет с помощью мышки нанести на график надпись у (х)

>> [X Y]

>> % Последняя команда выводит таблицу численного решения задачи.

 

Результаты решения. График решения задачи Коши (2.7) показан на рис. 2.3. Численное решение представлено в таблице 2.4, где приведены только отдельные узловые точки. В программе ode45 по умолчанию интервал разбивается на 40 точек с шагом h = 1/40 = 0.025.

 

Рис. 2.3

Таблица 2.4

хi	Метод Рунге-Кутта	Точное решение
0.0	1.0	1.0
0.1	1.2221	1.2221
0.2	1.4977	1.4977
0.3	1.8432	1.8432
0.4	2.2783	2.2783
0.5	2.8274	2.8274
0.6	3.5202	3.5202
0.7	4.3928	4.3928
0.8	5.4895	5.4895
0.9	6.8645	6.8645
1.0	8.5836	8.5836

 

Как следует из таблицы 2.4 численное решение программой ode45 является точным.

Варианты заданий. Построить график и вывести в виде таблицы решение задачи Коши на интервале [0; 1] методом Рунге-Кутта 4-го порядка. Данные взять из таблицы 2.5.

Таблица 2.5

№ п/п	f(x,y)	y0
1.		0.0
2.		0.1
3.		2.0
4.		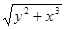0.3
5.		0.4
6.		0.0
7.		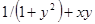0.1
8.		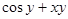0.2
9.		0.3
10.		0.4
11.		0.5
12.		0.0
13.		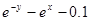0.5
14.		0.4
15.		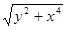0.3
16.		0.2
17.		0.1
18.		0.0
19.		0.1
20.		0.2
21.		0.3
22.		0.4
23.		0.5
24.		0.6
25.		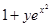0.7
26.		0.0
27.		0.1
28.		0.2
29.		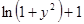0.3
30.		0.4

 

ГЛАВА 2. MATLAB в задачах вычислительной

Математики

Система MATLAB обладает большими возможностями программирования и комплексной визуализации результатов инженерных расчетов и научных исследований. В этой связи покажем применение богатых возможностей MATLAB в решении задач вычислительной математики. Развитие многих наук привело исследователей к необходимости численного решения различных проблем, т. е. применению численных методов. Численные методы создаются и исследуются высококвалифицированными специалистами – математиками и, как в системе MATLAB, предлагаются для применения в виде готового инструмента. Поэтому задачей данной главы является изложение основных идей численных методов и ознакомление с последовательностью применения численных процессов в современных компьютерных системах

Программы, реализующие какой-либо численный метод, необходимо записывать в М-файл. Если не дать имени М-файлу, то он запишется при выполнении программы в рабочую папку под именем Untitled (Безымянный). Такой ситуации следует избегать для исключения появления множества файлов с неопределенным именем. Рассмотрим решение некоторых важных проблем вычислительной математики.