Работа рассчитана на два-три занятия и состоит из нескольких этапов.
На первом этапе преподаватель вкратце напоминает теоретические основы численных методов вычисления криволинейных интегралов и раздает задания. Примерный перечень вариантов заданий представлен в приложении 1.
На втором этапе студенты знакомятся с методическими указаниями по выполнению лабораторной работы и начинают аналитически вычислять значения заданного криволинейного интеграла в рабочей тетради.
Рекомендация. Если аналитические вычисления вызывают затруднение, можно перейти к третьему этапу, оставив аналитические вычисления на дом.
Примеры аналитических вычислений:
1. Вычислить криволинейный интеграл  , где L – дуга параболы у 2 = 2 х, заключенная между точками (2, 2) и (8, 4) (рис.4).
, где L – дуга параболы у 2 = 2 х, заключенная между точками (2, 2) и (8, 4) (рис.4).
Это – криволинейный интеграл первого
рода, причем кривая интегрирования задана
явно. Найдем дифференциал дуги dl для
кривой у =  . Имеем:
. Имеем:
Рис. 4.
у¢ =  , dl =
, dl =  dx =
dx = 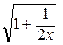 dx
dx
Следовательно, данный интеграл равен (2):
 =
= 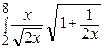 dx =
dx =  dx =
dx = 
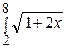 dx =
dx =
=  ∙
∙ 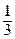
 =
= 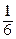 (17
(17 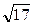 – 5
– 5 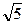 ).
).










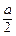
 2. Вычислить криволинейный интеграл
2. Вычислить криволинейный интеграл 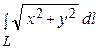 , где L – окружность х 2 + у 2 = ах (a > 0).
, где L – окружность х 2 + у 2 = ах (a > 0).
Для представления окружности х 2 + у 2 = ах
в каноническом виде выделим полный квадрат по х:
х 2 – ах +  + у 2 =
+ у 2 =  , т.е. (х –
, т.е. (х –  )2 + у 2 =
)2 + у 2 = 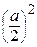 .
.
Это – окружность радиуса  с центром в точке (
с центром в точке ( , 0)
, 0)
График этой окружности представлен на рис. 5. Рис.5.
Введем полярные координаты x = r cos φ, y = r sin φ. Подынтегральная функция  в полярных координатах примет
в полярных координатах примет
вид  =
= 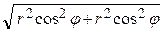 = r
= r
Тогда, т.к. х 2 + у 2 = ах, имеем: r 2 cos2 φ + r 2 sin2 φ = a r cos φ или
r (cos2 φ + sin2 φ) = a cos φ. Окончательно, уравнение окружности L в полярных координатах имеет вид: r = a cos φ. Соответственно, дифференциал дуги (4):
dl =  =
=  dφ = a dφ.
dφ = a dφ.
При этом (см. рис. 5): φ 
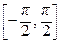 .
.
Подынтегральная функция  в полярных координатах примет
в полярных координатах примет
вид  =
= 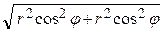 = r
= r
Таким образом,
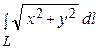 =
=  = а
= а 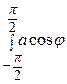 dφ = 2 а 2.
dφ = 2 а 2.
3. Вычислить криволинейный интеграл первого рода от функции трех переменных  , где L – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ π.
, где L – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ π.
Перейдем в подынтегральном выражении к переменной t. Имеем для подынтегральной функции
5 z – 2  = 5 t – 2
= 5 t – 2  = 3 t.
= 3 t.
Теперь выразим через t дифференциал dl (3):
dl = 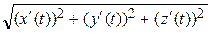 dt =
dt =  dt = =
dt = = 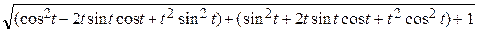 dt =
dt =
= 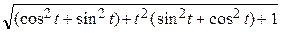 dt =
dt = 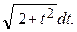
Таким образом,  =
= 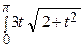 dt =
dt =
= 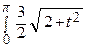 d (2 + t 2) =
d (2 + t 2) =  =
= 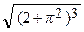 – 2
– 2  .
.
4. Вычислить криволинейный интеграл 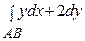 от точки А (0; 0) до точки В (1; 1) по кривым а) у = х, б) у = х 2, в) у =
от точки А (0; 0) до точки В (1; 1) по кривым а) у = х, б) у = х 2, в) у = 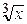 (рис.6).
(рис.6).








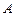
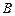





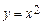



 а) Из уравнения линии у = х получаем dy = dx, поэтому
а) Из уравнения линии у = х получаем dy = dx, поэтому
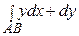 =
=  =
= 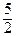 .
.
б) Из уравнения линии у = х 2 получаем dy =2 xdx, поэтому
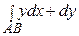 =
= 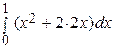 =
= 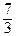 .
.
в) Из уравнения линии х = 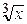 получаем dy =
получаем dy = 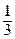
 dx, поэтому Рис.6.
dx, поэтому Рис.6.
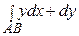 =
=  =
=  .
.
Таким образом, интеграл второго рода в общем случае зависит от вида кривой, соединяющей конечные точки.
5. Найти площадь области, ограниченной эллипсом x = a cos t, y = b sin t.
Площадь S области D, ограниченной кривой L, находят по формуле
S = 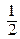
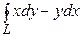 .
.
Поэтому, в нашем случае
S = 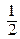
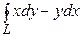 =
= 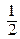
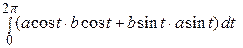 = =
= = 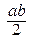
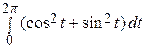 =
= 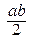
 = πab.
= πab.
Третий этап работы состоит в написании и отладке программы на знакомом (и доступном для рабочей ПЭВМ) языке программирования. Примеры программ на PASCALе вычисления криволинейных интегралов, рассмотренных в примерах, представлены ниже. Эти программы можно использовать в качестве тестовых при выполнении собственных заданий, т.к. отличия в программах будут незначительными.
Замечания. Для получения «красивых» таблиц
а) в строковых константах (в кавычках) при наборе их латиницей количество символов должно быть таким же, как и в примере, где они набраны кириллицей;
б) количество пробелов в строковых константах также должно быть таким же, как и в примере. Для этого последовательность количества пределов в строковой константе представлена в комментарии.
Пример 1. Вычислить криволинейный интеграл  , где L –
, где L –
дуга параболы у 2 = 2 х, заключенная между точками (2, 2) и (8, 4).
program ivanov_kri1_1; {по параболе АВ: у*у=2х, А(2,2), В(8,4)}
Var
x0,xn,dx,dy,s,xi,xc,yc,dl,tr: real;
n,i: integer;
function piv(x,y,dl: real): real; {подынтегральное выражение x / y dl }
Begin
piv:=x/y*dl
end;
function put(x: real): real; {кривая интегрирования sqrt(2x)}
Begin
put:= sqrt(2*x)
end;
Begin
writeln (‘введите пределы интегрирования по х: x0 и xn’);
read (x0,xn); {ввод x0,xn }
tr:=(17*sqrt(17) – 5*sqrt(5))/6; (аналитическое решение)}
writeln (‘введите число разбиений n отрезка [a,b]’);
read (n); {ввод n }
writeln( ‘ Р Е З У Л Ь Т А Т Ы’);{впереди 20 пробелов}
writeln;
writeln (‘ n точн.знач. числ.реш. абс.ош. отн.ош’);{4,7,2,3,5 пробелов}
writeln;
dx:=(xn–x0)/n;
s:=0; {интегральная сумма}
xi:=x0; {начальная точка частичных отрезков}
xс:=x0–dx/2; {серединная точка частичных отрезков}
for i:=1 to n do
Begin
xс:=xc+dx;
yc:=put(xc); {значение подынтегр. функции в серединной точке}
dy:= put(xi+dx) – put(xi); {приращение пути на частичном отрезке}
dl:=sqrt(dx*dx + dy*dy); {≈ длине дуги для частичного отрезка}
s:= s+ piv(xc,yc,dl)
xi:=xi+dx;
end;
writeln (n:6,tr:14:6,s:12:6,abs(s–tr):11:6,abs((s–tr)/tr):12:6);
readln;
readln;
end.
Окно вывода отлаженной программы должно иметь вид:



 , где L – дуга параболы у 2 = 2 х, заключенная между точками (2, 2) и (8, 4) (рис.4).
, где L – дуга параболы у 2 = 2 х, заключенная между точками (2, 2) и (8, 4) (рис.4).
 . Имеем:
. Имеем: , dl =
, dl =  dx =
dx = 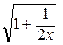 dx
dx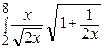 dx =
dx =  dx =
dx = 
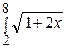 dx =
dx =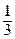
 =
= 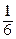 (17
(17 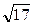 – 5
– 5 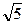 ).
).









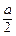
 2. Вычислить криволинейный интеграл
2. Вычислить криволинейный интеграл 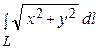 , где L – окружность х 2 + у 2 = ах (a > 0).
, где L – окружность х 2 + у 2 = ах (a > 0). + у 2 =
+ у 2 =  )2 + у 2 =
)2 + у 2 = 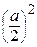 .
. в полярных координатах примет
в полярных координатах примет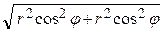 = r
= r =
=  dφ = a dφ.
dφ = a dφ.
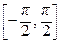 .
. = а
= а 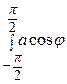 dφ = 2 а 2.
dφ = 2 а 2. , где L – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ π.
, где L – дуга кривой, заданной параметрически x = t cos t, y = t sin t, z = t, 0 ≤ t ≤ π. = 3 t.
= 3 t.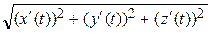 dt =
dt =  dt = =
dt = = 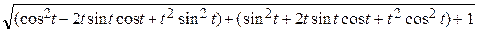 dt =
dt =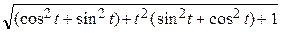 dt =
dt = 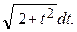
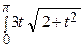 dt =
dt =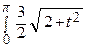 d (2 + t 2) =
d (2 + t 2) =  =
= 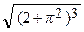 – 2
– 2  .
.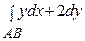 от точки А (0; 0) до точки В (1; 1) по кривым а) у = х, б) у = х 2, в) у =
от точки А (0; 0) до точки В (1; 1) по кривым а) у = х, б) у = х 2, в) у = 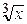 (рис.6).
(рис.6).






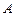
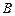


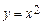


 а) Из уравнения линии у = х получаем dy = dx, поэтому
а) Из уравнения линии у = х получаем dy = dx, поэтому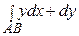 =
=  =
= 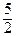 .
.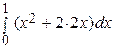 =
= 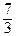 .
. dx, поэтому Рис.6.
dx, поэтому Рис.6. =
=  .
.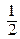
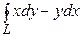 .
.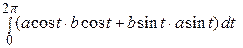 = =
= = 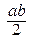
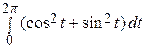 =
=  = πab.
= πab.


