Определение 2.3. Случайная величина, обозначаемая X, называется дискретной, если она принимает конечное либо счетное множество значений, т.е. множество 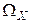 – конечное либо счетное множество.
– конечное либо счетное множество.
Рассмотрим примеры дискретных случайных величин.
1. Однократно бросают две монеты. Число выпадений гербов в этом эксперименте – случайная величина Х. Ее возможные значения 0,1,2, т. е.  – конечное множество.
– конечное множество.
2. Регистрируется число вызовов "Скорой помощи" в течение некоторого заданного промежутка времени. Случайная величина Х – число вызовов. Ее возможные значения 0, 1, 2, 3,...,т.е. 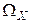 ={0,1,2,3,...}– счетное множество.
={0,1,2,3,...}– счетное множество.
3. В группе 25 студентов. В какой-то день регистрируется число студентов, пришедших на занятия, – случайная величина Х. Ее возможные значения: 0, 1, 2, 3,...,25 т.е. 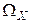 ={0, 1, 2, 3,..., 25}.
={0, 1, 2, 3,..., 25}.
Хотя все 25 человек в примере 3 пропустить занятия не могут, но случайная величина Х принимать это значение может. Это означает, что значения случайной величины обладают различной вероятностью.
Рассмотрим математическую модель дискретной случайной величины.
Пусть проводится случайный эксперимент, которому соответствует конечное или счетное пространство элементарных событий 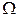 . Рассмотрим отображение этого пространства на множество действительных чисел, т. е. каждому элементарному событию
. Рассмотрим отображение этого пространства на множество действительных чисел, т. е. каждому элементарному событию  поставим в соответствие некоторое действительное число
поставим в соответствие некоторое действительное число  ,
,  . Множество чисел
. Множество чисел  при этом может быть конечным или счетным, т. е.
при этом может быть конечным или счетным, т. е.  или
или 
Система подмножеств, в которую входит любое подмножество 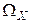 , в том числе одноточечное, образует
, в том числе одноточечное, образует  -алгебру
-алгебру 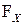 числового множества
числового множества 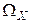 (
(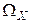 – конечно или счетно).
– конечно или счетно).
Поскольку любому элементарному событию  поставлены в соответствие определенные вероятности рi (в случае конечного
поставлены в соответствие определенные вероятности рi (в случае конечного 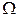 все
все  ), причем
), причем  , то и каждому значению
, то и каждому значению  случайной величины
случайной величины 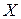 можем поставить в соответствие определенную вероятность рi, такую, что
можем поставить в соответствие определенную вероятность рi, такую, что  .
.
Пусть х – произвольное действительное число. Обозначим РХ(х) вероятность того, что случайная величина Х приняла значение, равное х, т.е. РХ(х)=Р(Х=х). Тогда функция РХ(х) может принимать положительные значения лишь при тех значениях х, которые принадлежат конечному либо счетному множеству  , а при всех остальных значениях
, а при всех остальных значениях  вероятность этого значения РХ(х)=0.
вероятность этого значения РХ(х)=0.
Итак, мы определили множество значений 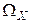 ,
,  -алгебру
-алгебру 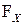 как систему любых подмножеств
как систему любых подмножеств 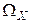 и каждому событию { X = х } сопоставили вероятность
и каждому событию { X = х } сопоставили вероятность  дпя любых
дпя любых 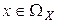 , т.е. построили вероятностное пространство
, т.е. построили вероятностное пространство  .
.
Например, пространство 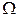 элементарных событий эксперимента, состоящего в двукратном подбрасывании симметричной монеты, состоит из четырех элементарных событий:
элементарных событий эксперимента, состоящего в двукратном подбрасывании симметричной монеты, состоит из четырех элементарных событий: 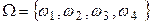 , где
, где

 при двукратном подбрасывании монеты выпали две решетки
при двукратном подбрасывании монеты выпали две решетки 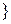 ;
; 
 при двукратном подбрасывании монеты выпали два герба
при двукратном подбрасывании монеты выпали два герба 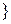 ;
;

 при первом подбрасывании монеты выпала решетка, а при втором – герб
при первом подбрасывании монеты выпала решетка, а при втором – герб 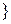 ;
;
 =
= 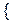 при первом подбрасывании монеты выпал герб, а при втором – решетка
при первом подбрасывании монеты выпал герб, а при втором – решетка 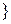 .
.
Пусть случайная величина Х – число выпадений решетки. Она определена на 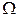 и множество ее значений
и множество ее значений  . Все возможные подмножества
. Все возможные подмножества 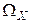 , в том числе и одноточечные, образуют
, в том числе и одноточечные, образуют  - алгебру, т.е.
- алгебру, т.е. 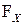 ={Ø, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}}.
={Ø, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}}.
Вероятность события { Х=хi }, і = 1,2,3, определим как вероятность появления события, являющегося его прообразом:
 ;
;
 ;
;
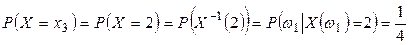 .
.
Таким образом, на элементарных событиях { X = хi } задали числовую функцию РХ, так, что  .
.
Определение 2.4. Законом распределения дискретной случайной величины называется совокупность пар чисел (хi, рi), где хi – возможные значения случайной величины, а рi – вероятности, с которыми она принимает эти значения, причем  .
.
Простейшей формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующиеим вероятности:

Такая таблица называется рядом распределения. Чтобы придать ряду распределения более наглядный вид, его изображают графически: на оси Ох наносят точки хi и проводят из них перпендикуляры длиной рi. Полученные точки соединяют и получают многоугольник, который является однойиз форм закона распределения (рис. 2.1).

Рис. 2.1
Таким образом, для задания дискретной случайной величины нужно задать ее значения и соответствующиеим вероятности.
Пример 2.2. Денежный приемник автомата срабатывает при каждом опускании монеты с вероятностью р. Как только он сработал, монеты не опускают. Пусть Х – число монет, которые надо опустить до срабатывания денежного приемника автомата. Построить ряд распределения дискретной случайной величины Х.
Решение. Возможные значения случайной величины Х: х1 = 1, х2 = 2,..., хк=к, … Найдем вероятности этих значений: р1 – вероятность того, что денежный приемник сработает при первом опускании, и р1 =р; р2 – вероятность того, что будут произведены две попытки. Для этого нужно, чтобы: 1) при первой попытке денежный приемник не сработал; 2) при второй попытке – сработал. Вероятность этого события равна (1–р)р. Аналогично  и так далее,
и так далее,  . Ряд распределения Х примет вид
. Ряд распределения Х примет вид

| 1
| 2
| 3
| …
| к
| …
|
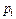
| р
| qp
| q2 p
|
| qr-1 p
|
|
Заметим, что вероятности рк образуют геометрическую прогрессию со знаменателем: 1–p=q, q<1, поэтому такое распределение вероятностей называется геометрическим.
ІІредположим далее, что построена математическая модель  эксперимента, описываемого дискретной случайной величиной Х, и рассмотрим вычисление вероятностей наступления произвольных событий
эксперимента, описываемого дискретной случайной величиной Х, и рассмотрим вычисление вероятностей наступления произвольных событий  .
.
Пусть произвольное событие  содержит конечное либо счетное множество значений хi: A= { х1, х2,..., хi,... }.Событие А можно представить в виде объединения несовместных событий вида
содержит конечное либо счетное множество значений хi: A= { х1, х2,..., хi,... }.Событие А можно представить в виде объединения несовместных событий вида  :
:  . Тогда, применяя аксиому Колмогорова 3, получаем
. Тогда, применяя аксиому Колмогорова 3, получаем
 ,
,
так как вероятности наступления событий  мы определили равными вероятностям появления событий, являющихся их прообразами. Это значит, что и вероятность любого события
мы определили равными вероятностям появления событий, являющихся их прообразами. Это значит, что и вероятность любого события  ,
,  , можно вычислить по формуле
, можно вычислить по формуле 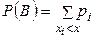 , так как это событие представимо в виде, объединения событий
, так как это событие представимо в виде, объединения событий  , где
, где  .
.
Тогда и функция распределения F(х) = Р(–  <Х<х) находится по формуле
<Х<х) находится по формуле  . Отсюда следует, что функция распределения дискретной случайной величины Х разрывна и возрастает скачками, т. е. является ступенчатой функцией (рис. 2.2):
. Отсюда следует, что функция распределения дискретной случайной величины Х разрывна и возрастает скачками, т. е. является ступенчатой функцией (рис. 2.2):

Рис. 2.2

Если множество 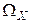 конечно, то число слагаемых в формуле
конечно, то число слагаемых в формуле  конечно, если же
конечно, если же 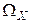 счётно, то и число слагаемых счетно.
счётно, то и число слагаемых счетно.
Пример 2.3. Техническое устройство состоит из двух элементов, работающих независимо друг от друга. Вероятность выходаиз строя первого элемента за время Т равна 0,2, а вероятность выхода второго элемента – 0,1. Случайная величина Х – число отказавших элементов за время Т. Найти функцию распределения случайнойвеличины и построить ее график.
Решение. Пространство элементарных событий 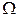 эксперимента, состоящего в исследовании надежности двух элементов технического устройства, определяется четырьмя элементарными событиями
эксперимента, состоящего в исследовании надежности двух элементов технического устройства, определяется четырьмя элементарными событиями  ,
,  ,
,  ,
,  :
:  – оба элемента исправны;
– оба элемента исправны;  – первый элемент исправен, второй неисправен;
– первый элемент исправен, второй неисправен;  – первый элемент неисправен, второй исправен;
– первый элемент неисправен, второй исправен;  – оба элемента неисправны. Каждоеиз элементарных событий можно выразить через элементарные события пространств
– оба элемента неисправны. Каждоеиз элементарных событий можно выразить через элементарные события пространств  и
и  , где
, где  – первый элемент исправен;
– первый элемент исправен;  – первый элемент вышел из строя;
– первый элемент вышел из строя;  – второй элемент исправен;
– второй элемент исправен;  – второй элемент вышел из строя. Тогда
– второй элемент вышел из строя. Тогда  , и таккак элементы технического устройства работают независимо друг от друга, то
, и таккак элементы технического устройства работают независимо друг от друга, то
 ;
;
 ;
;
 ;
;
 .
.
Очевидно, что множество значений случайной величины Х – число отказавших элементов – состоит из трех элементов: х1 = 0, х2 = 1, х3 =2 т.е.  . Распределение вероятностей случайной величины Х на множестве
. Распределение вероятностей случайной величины Х на множестве 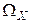 зададим так, чтобы вероятность наступления события {
зададим так, чтобы вероятность наступления события {  } была равна вероятности наступления прообраза этого события, т.е.
} была равна вероятности наступления прообраза этого события, т.е.  i =1, 2, 3:
i =1, 2, 3:
 , так как
, так как  – прообраз элемента
– прообраз элемента  ,
,
 , так как прообразом элемента
, так как прообразом элемента  является множество
является множество  ;
;
 , так как прообразом элемента
, так как прообразом элемента  является элементарное событие
является элементарное событие  . Полученный закон распределения представим в виде таблицы распределения:
. Полученный закон распределения представим в виде таблицы распределения:

|
|
|
|
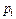
| 0,72
| 0,26
| 0,02
|

Согласно определению,функция распределения равна:

График функции F(x) представлен на рисунке 2.3.
Ответ: функция распределения 

Рис. 2.3
Вопросы для самопроверки
1. Сформулируйте определение дискретной случайной величины 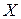 .
.
2. Как определяется вероятность события 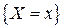 ?
?
3. Сформулируйте определение закона распределения дискретной случайной величины 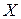 .
.
4. В какой форме задается закон распределения дискретной случайной величины 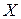 ?
?
5. Что является графиком ряда распределения?
6. Как вычислить вероятность события 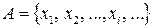 ?
?
7. Как вычислить функцию распределения 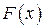 дискретной случайной величины
дискретной случайной величины 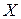 и построить ее график?
и построить ее график?
8. Чему равна вероятность того, что значения дискретной случайной величины 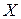 принадлежат промежутку
принадлежат промежутку 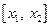 ?
?



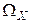 – конечное либо счетное множество.
– конечное либо счетное множество. – конечное множество.
– конечное множество.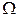 . Рассмотрим отображение этого пространства на множество действительных чисел, т. е. каждому элементарному событию
. Рассмотрим отображение этого пространства на множество действительных чисел, т. е. каждому элементарному событию  поставим в соответствие некоторое действительное число
поставим в соответствие некоторое действительное число  ,
,  . Множество чисел
. Множество чисел  при этом может быть конечным или счетным, т. е.
при этом может быть конечным или счетным, т. е.  или
или 
 -алгебру
-алгебру 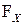 числового множества
числового множества  поставлены в соответствие определенные вероятности рi (в случае конечного
поставлены в соответствие определенные вероятности рi (в случае конечного  ), причем
), причем  , то и каждому значению
, то и каждому значению  случайной величины
случайной величины 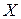 можем поставить в соответствие определенную вероятность рi, такую, что
можем поставить в соответствие определенную вероятность рi, такую, что  .
. , а при всех остальных значениях
, а при всех остальных значениях  вероятность этого значения РХ(х)=0.
вероятность этого значения РХ(х)=0. дпя любых
дпя любых 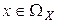 , т.е. построили вероятностное пространство
, т.е. построили вероятностное пространство  .
.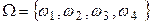 , где
, где
 при двукратном подбрасывании монеты выпали две решетки
при двукратном подбрасывании монеты выпали две решетки 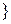 ;
; 

 =
=  при первом подбрасывании монеты выпал герб, а при втором – решетка
при первом подбрасывании монеты выпал герб, а при втором – решетка  . Все возможные подмножества
. Все возможные подмножества  ;
; ;
;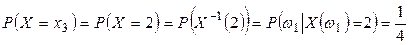 .
. .
.


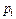



 и так далее,
и так далее,  . Ряд распределения Х примет вид
. Ряд распределения Х примет вид эксперимента, описываемого дискретной случайной величиной Х, и рассмотрим вычисление вероятностей наступления произвольных событий
эксперимента, описываемого дискретной случайной величиной Х, и рассмотрим вычисление вероятностей наступления произвольных событий  .
. :
:  . Тогда, применяя аксиому Колмогорова 3, получаем
. Тогда, применяя аксиому Колмогорова 3, получаем ,
, ,
,  , можно вычислить по формуле
, можно вычислить по формуле 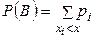 , так как это событие представимо в виде, объединения событий
, так как это событие представимо в виде, объединения событий  .
. <Х<х) находится по формуле
<Х<х) находится по формуле  . Отсюда следует, что функция распределения дискретной случайной величины Х разрывна и возрастает скачками, т. е. является ступенчатой функцией (рис. 2.2):
. Отсюда следует, что функция распределения дискретной случайной величины Х разрывна и возрастает скачками, т. е. является ступенчатой функцией (рис. 2.2):

 и
и  , где
, где  – первый элемент исправен;
– первый элемент исправен;  – первый элемент вышел из строя;
– первый элемент вышел из строя;  – второй элемент исправен;
– второй элемент исправен;  – второй элемент вышел из строя. Тогда
– второй элемент вышел из строя. Тогда  , и таккак элементы технического устройства работают независимо друг от друга, то
, и таккак элементы технического устройства работают независимо друг от друга, то ;
; ;
; ;
; .
. } была равна вероятности наступления прообраза этого события, т.е.
} была равна вероятности наступления прообраза этого события, т.е.  i =1, 2, 3:
i =1, 2, 3: , так как
, так как  ,
, , так как прообразом элемента
, так как прообразом элемента  является множество
является множество  ;
; , так как прообразом элемента
, так как прообразом элемента  является элементарное событие
является элементарное событие 



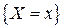 ?
?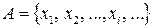 ?
?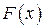 дискретной случайной величины
дискретной случайной величины 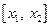 ?
?


