| Двухполюсники
| Линейная связь
| Нелинейная связь
|
| Источник напряжения, управляемый
напряжением
| 
| 
|
| Источник напряжения, управляемый током
| 
| 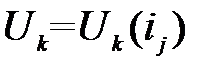
|
| Источник тока,
управляемый током
| 
| 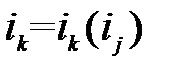
|
| Источник тока,
управляемый
напряжением
| 
|  
|
| Резистор
| 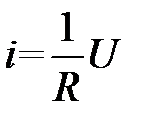 , ,
 , ,

|  , ,

|
| Конденсатор
|  , ,
 , ,

|  , ,
 , ,

|
| Катушка
индуктивности
|  , ,
 , ,

|  , ,

|
| Независимый
источник напряжения
| 
|
|
| Независимый
источник тока
| 
|
|
8.2. Методы формирования математических моделей ИС
Как было отмечено выше, в основе методов формирования математических моделей лежат законы Кирхгофа. Для каждого метода формирования ММС характерны свои правила выбора системы исходных топологических уравнений и базиса независимых переменных.
В зависимости от этого выбора полученные математические модели - системы уравнений – могут отличаться по виду и по размерности.
Примечание: в наиболее общем случае они представляют собой системы интегро-дифференциальных уравнений. Такие модели целесообразно использовать в открытых системах моделирования, допускающих применение нескольких методов решения. В процессе решения полученные аналитические модели подвергаются преобразованиям путем алгебраизации. В результате получаются либо системы конечно-разностных уравнений, либо системы алгебраических выражений. Алгебраизированные системы исходных уравнений, в свою очередь, подвергаются линеаризации. Решение таких систем уравнений непосредственно реализуется в виде алгоритмов и программ.
Таким образом, ММС можно классифицировать по виду получающихся выражений, выделив ряд классов:
· Системы нелинейных интегро-дифференциальных уравнений;
· Системы нелинейных дифференциальных уравнений;
· Системы нелинейных алгебраических уравнений;
· Системы линейных алгебраических уравнений;
· Системы алгебраических выражений.
В среде разработчиков наибольшее распространение получил Метод узловых потенциалов (МУП).
В методе узловых потенциалов в качестве независимых переменных используются потенциалы внутренних узлов схемы относительно некоторого опорного узла, потенциал которого считается равным нулю. Внутренним узлом называется точка соединения двух или более компонентов схемы, которая не связана непосредственно с источником напряжения.
В основе метода лежит первый закон Кирхгофа.
Если токи выразить через узловые потенциалы, то для схемы, содержащей Nвнутренних узлов, с помощью первого закона Кирхгофа мы получим систему Nуравнений относительно неизвестных– потенциалов внутренних узлов. В векторной форме эта система будет иметь видI(U)=0, гдеI=(I1, I2, …, IN)– вектор узловых токов;U=(U1, U2, …, UN) – вектор узловых потенциалов; j-я компонента вектора I определяется как алгебраическая сумма токов ветвей, связанных с j-м узлом:
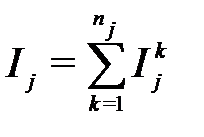 , (8.1)
, (8.1)
гдеIjk–ток k-й ветви, связанной сj-м узлом;nj– количество ветвей, связанных с j-м узлом.
При наличии в схеме емкостей и индуктивностей метод узловых потенциалов позволяет получить математическую модель схемы в виде системы интегро-дифференциальных уравнений.
Одним из способов решения такой системы является способ, основанный на использовании неявных формул интегрирования. Основная идея способа состоит в сведении системы интегро-дифференциальных уравнений на каждом шаге интегрирования к системе нелинейных алгебраических уравнений. Исходя из этого, на (n+1)-м шаге интегрирования на основании метода узловых потенциалов мы можем формировать систему нелинейных алгебраических уравнений относительно вектора узловых потенциаловUn+1:
 .
.
Для решения данной системы в настоящее время, как правило, используется итерационный метод Ньютона-Рафсона, который будет подробно рассмотрен далее. При этом на m-й итерации вычисляется вектор приращений узловых потенциалов ΔUn+1,m путем решения системы линейных алгебраических уравнений:
 (8.2)
(8.2)
где  – матрица узловых проводимостей (матрица Якоби).
– матрица узловых проводимостей (матрица Якоби).
Далее вычисляются скорректированные значения векторов узловых потенциалов на (n+1)-м шаге
 .
.
Итерационный процесс обычно заканчивается, когда норма вектора приращений узловых потенциалов оказывается меньше наперед заданной величины
 .
.
На основании вышеизложенного можно сделать вывод, что при использовании метода узловых потенциалов для анализа схемы необходимо формировать не сами узловые уравнения, а систему (8.1), с помощью которой они решаются. Таким образом, следует иметь алгоритмы формирования матрицы Якоби и вектора узловых токов.
Заметим, что j-я компонента вектора узловых токов I определяется как алгебраическая сумма токов ветвей (т.е. выводов компонентов), связанных с j-м узлом, по формуле (8.2); j,i-й элемент матрицы полных узловых проводимостей определяется как алгебраическая сумма частных производных токов выводов компонентов, связанных с j-м узлом, по напряжению в i-м узле:

Отсюда следует, что вектор узловых токов и матрица полных узловых проводимостей могут быть вычислены при последовательном обращении к математическим моделям всех компонентов схемы. При этом каждый компонент дает определенные составляющие для элементов вышеуказанных вектора и матрицы.
Исходными данными для модели являются параметры модели и значение напряжений на выходах компонента на pпредыдущих шагах интегрирования, где p– порядок формулы интегрирования. Если схема замещения компонента содержит индуктивности, то для модели такого компонента необходимы значения токов через индуктивности на p предыдущих шагах интегрирования.
Рассмотрим действия, которые производятся при обращении к модели k-ого компонента, имеющего n выводов и подсоединенного в схеме к узламj1, j2, …, jn.
Вычисляются токи выводов компонента 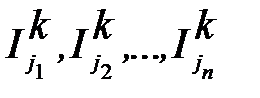 по аналитическим зависимостям, связывающим токи выводов и напряжения на выводах компонента. Например, для резистора, включенного между узлами j1иj2,
по аналитическим зависимостям, связывающим токи выводов и напряжения на выводах компонента. Например, для резистора, включенного между узлами j1иj2,
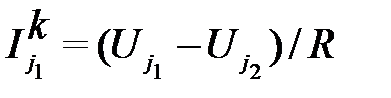 ,
,
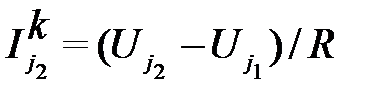 .
.
Эти токи отличаются только знаком  .
.
Токи выводов суммируются с соответствующими элементами вектора узловых токов:  ,i=1,2,…,n.
,i=1,2,…,n.
Вычисляются производные токов выводов по напряжениям на выводах компонента 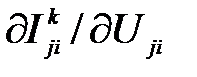 ,i,l=1,2,…,n.Для резистора эти величины равны
,i,l=1,2,…,n.Для резистора эти величины равны
 ,
, 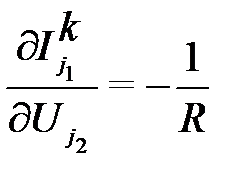 ,
,  ,
, 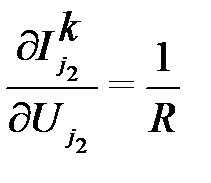 .
.
Вычисленные производные суммируются с соответствующими элементами матрицы полных узловых проводимостей
 , i,l=1,2,…,n.
, i,l=1,2,…,n.
Следует отметить, что рассмотренные операции суммирования производятся только для внутренних узлов схемы.
Ряд ограничений, свойственных методу узловых потенциалов, носит, как правило, чисто теоретический характер и практически несущественен. Многие из этих ограничений при необходимости могут быть устранены с помощью специальных приемов. Например, при наличии в схеме «подвешенного» источника напряжения можно последовательно с ним включить два резистора, одинаковых по величине, но противоположных по знаку, затем любой из них добавить к источнику напряжения и заменить его эквивалентным источником тока. При этом в схеме появится один дополнительный узел.
8.2.1. Пример формирования ММС МУП
Составим математическую модель для принципиальной электрической схемы(см. рис. 8.2).
Составим систему уравнений токов узлов 1, 2 относительно потенциалов узлов φiв соответствии с МУП.
Токи ветвей описываются следующим образом
 ;
;  ;
;  ;
; 

Рис.8.2. Принципиальная электрическая схема
Подставив эти выражения в систему, получим:
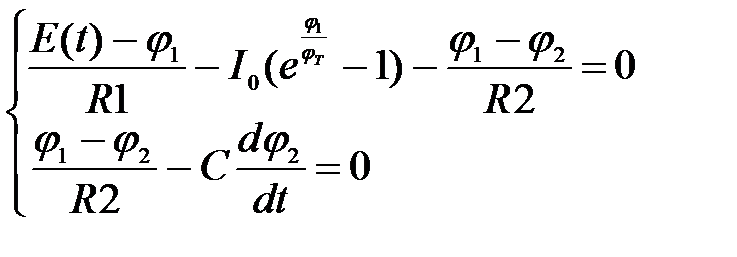
Для этого примера общий вид полученной системы уравнений 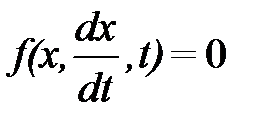 .
.
В частном случае линейной резистивной схемы, т. е. схемы, состоящей из линейных резисторов, источников тока, управляемых напряжением по линейному закону и независимых источников тока, математической моделью будет система линейных алгебраических уравнений видаY⸱φ+J=0.
Здесь: Y– матрица узловых проводимостей,φ–вектор независимых переменных – узловых потенциалов, J– вектор независимых источников тока.
Алгоритм формирования матрицы узловых проводимостей и вектора независимых источников тока:
1) Обнуляем массивы Y, J, отведённые под матрицу узловых проводимостей и вектор независимых источников тока;
2) Просматриваем все ветви, входящие в схему.
Если ветвь, включённая между узлами i, j резистор с проводимостью y, то к элементам ii, ij,ji, jj массива Y прибавляем y,-y,-y,y.
Если ветвь, включённая между узлами i, jисточник тока, управляемый напряжением ветви, включённой между узламиk, m с коэффициентом g, то к элементам ik,im,jk,jmмассива Y прибавляем g,-g, -g, g.
Если ветвь, включённая между узлами i, jнезависимый источник тока G, то к элементам i, jмассива J добавляем G, -G.
8.3. Специфика математических моделей БИС
· Большая размерность
Известно, степень интеграции ИС постоянно растёт, следовательно, растёт размерность соответствующих математических моделей ИС, характеризующихся порядком соответствующих систем уравнений.
· Разреженность
При представлении математических моделей ИС в матричной форме, не более 10% элементов матрицы оказываются ненулевыми. Такое свойство модели называется разреженностью. Очевидно, что хранить нулевые элементы таких матриц и выполнять операции с ними нецелесообразно. Поэтому в практике схемотехнического моделирования нашли применение способы хранения только ненулевых элементов матриц.
· Жёсткость
Элементы схем имеют большой разброс номинальных значений параметров. Это ведет к большому разбросу собственных значений матриц параметров элементов схем (например, матрицы узловых проводимостей при применении метода узловых потенциалов). Если число обусловленности матрицы
 ,
,
где λmax и λmin– соответственно максимальное и минимальное собственные значения матрицы, то уравнение называется жестким.
Жесткость уравнений обусловливает трудности их решения.
8.4. Основы динамического анализа электронных схем
Целью динамического анализа является моделирование процессов распространения электрических сигналов в электронных схемах.
Задачу моделирования переходных процессов в электронных схемах можно свести к задаче интегрирования системы обыкновенных дифференциальных первого порядка с начальными условиями, т.е. к задаче Коши.
Построение алгоритмов численного интегрирования основано на дискретизации задачи путем замены непрерывного временного интервала интегрирования на дискретный. Для этого делят интервал времени моделирования [a, b] на небольшие приращения (вводят дискретный набор точекti). Каждое приращение hk=Δtk называют шагом интегрирования. Производные заменяются конечно-разностными алгебраическими выражениями. В результате исходная система ОДУ заменяется системой конечно-разностных уравнений. Под конечно-разностными уравнениями понимаются алгебраические соотношения между компонентами, отнесенные к узлам. При этом приближенное значение переменнойxk+1вычисляется с учетом значений величин, найденных ранее. Если формула, по которой вычисляетсяxk+1, зависит явно только отxk, то метод называется одношаговым. Если xk+1вычисляется по двум предыдущим значениямxk,xk+1, то метод называется двухшаговым. Следовательно, методы можно классифицировать по признаку числа предыдущих значений переменных, которые используются для вычисления очередного значения переменной. Поскольку численный метод не позволяет найти точное решениеx(tk), обозначим вычисленное значение для момента времени t=tk какxk. Равенствоεk = ||x(tk) - xk||называют локальной ошибкой при t=tk. Локальная ошибка состоит из двух компонентов – методической ошибки и ошибки округления, в предположении, что значение x на предыдущем шаге известно точно. Методическую ошибку называют также алгоритмической, поскольку она зависит от вида численного алгоритма разностной аппроксимации производных.
Локальная ошибка округления зависит от типа вычислительной машины, т.е. она не может быть уменьшена для данной машины, однако различные методы интегрирования по-разному влияют на ошибку округления. Важно помнить, что общая ошибка округления при t=tkне равна сумме локальных ошибок округления, возникающих на каждом шаге. Поэтому для сравнения точности двух алгоритмов необходимо сравнивать их в одни и те же моменты времени tk при одном и том же начальном состоянии.
Помимо локальной ошибки рассматривается также глобальная ошибка. Она является разностью между вычисленным и «теоретическим» решениями. Эта ошибка состоит из двух частей – локальной ошибки и распространяемой ошибки. Глобальная ошибка в узле tk+1– это глобальная ошибка в узлеtk, умноженная на некоторую величину, называемую множителем перехода, плюс локальная ошибка в узлеtk+1. При этом с увеличением числа шагов как методическая, так и ошибка округления могут накапливаться. Метод, обладающий свойством уменьшения ошибки округления при увеличении числа шагов, называется численно-устойчивым. В противном случае он является численно-неустойчивым. Устойчивость метода, как правило, зависит от выбора величины шага интегрирования. В этом случае метод относят к классу условно-устойчивых. Если метод устойчив при любом шаге интегрирования, то его относят к классу глобально (абсолютно, А-устойчивых) методов.
Рассмотрим три простейших метода численного интегрирования. Это:
1) Явный метод Эйлера;
2) Неявный метод Эйлера;
3) Метод трапеций.
Методы Эйлера относятся к классу методов Тейлора первого порядка, поскольку основаны на разложении функции в ряд Тейлора и отбрасывании членов второго и следующих порядков малости. Их также называют методами прямоугольников. Методы основаны на аппроксимации подынтегральной функции полиномом нулевой степени – константой на заданном отрезке интервала. Для такой аппроксимации достаточно одной точки – любого значения подынтегральной функции в любом узле; это значение считается постоянным на всем промежутке между соседними узлами. При выборе левой или правой границ шага разбиения в качестве значения на всем частичном интервале локальные методические ошибки имеют один и тот же порядок.
В методе трапеций используются обе границы частичного интервала. На каждом элементарном отрезке аргумента x участок кривой интегрирования представляет собой отрезок прямой – две ординаты и отрезок оси абсцисс вместе с этой прямой ограничивают фигуру трапецеидальной формы, что и дает название этому методу кусочно-линейной аппроксимации подынтегральной функции. Приближенное значение интеграла определяется площадью трапеции.
 подробно о методах:
подробно о методах:  системы обыкновенных дифференциальных уравнений представимы либо в общем виде, либо в форме Коши.
системы обыкновенных дифференциальных уравнений представимы либо в общем виде, либо в форме Коши.
Общий вид:

Форма Коши:
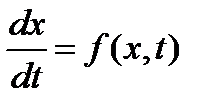
Производную  на основании известной теоремы о среднем в интервале tn, tn+1можно заменить отношением приращенийΔx/Δt, где
на основании известной теоремы о среднем в интервале tn, tn+1можно заменить отношением приращенийΔx/Δt, где
 ,
,
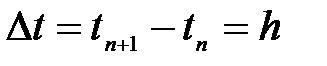 .
.
Примечание: в дальнейшем будем считать за правило:x(tn) – точное значение в момент времени tn, где n – номер узла, xn– приближённое значение.
Тогда, определяя производную для левой точки интервала, получим следующие выражения:
8.4.1. Явный метод Эйлера
Общий вид:
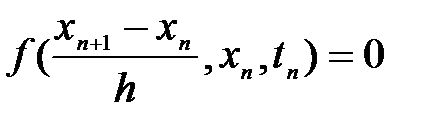
Форма Коши:

Определяя производную для правой точки интервала, получим:
8.4.2. Неявный метод Эйлера
Общий вид:

Форма Коши:

Выражения для явного метода Эйлера применительно к системе уравнений в форме Коши приводит к набору алгебраических функций; остальные выражения – системы трансцендентных нелинейных уравнений.
8.4.3. Метод трапеций
Суммируя выражения для явного и неявного методов Эйлера, получим формулы метода трапеций.
Общий вид:

Форма Коши:
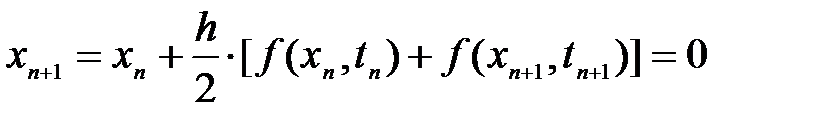
8.4.4. Оценка локальной методической погрешности ЯМЭ и НЯМЭ
Поскольку производная  определяется полиномом ряда Тейлора первой степени, то локальная ошибка метода определяется следующими членами полинома:
определяется полиномом ряда Тейлора первой степени, то локальная ошибка метода определяется следующими членами полинома:
Для явного метода Эйлера:

Для неявного метода Эйлера:

Данные методы –одного порядка точности. Здесьtn<τ<tn+1.
Выводы:
· Очевидно, что точность методов интегрирования зависит от величины шага интегрирования;
· Очевидно, что точность методов первого порядка Эйлера невысока, так что при их применении для обеспечения малой локальной методической ошибки следует интегрировать с малой величиной шага;
· Очевидно также, что локальная методическая ошибка метода трапеций на порядок меньше в силу того, что методические ошибки явного и неявного методов Эйлера имеют противоположные знаки;
· Очевидно также, что при малых значениях вторых производных и малой величине шага локальная методическая ошибка может оказаться существенно меньше заданной;
· Очевидно также, что для сохранения локальной методической ошибки в заданных пределах требуется выбирать шаг, учитывая вторую производную;
· Очевидно также, что в процессе интегрирования можно управлять величиной шага интегрирования с целью сокращения общего числа шагов.
В итоге решение системе уравнений вида f(x)=0.
Такие системы, как правило, решаются итерационными методами.
8.5. Итерационные методы решения систем нелинейных алгебраических уравнений
В основе итерационных методов решения систем нелинейных уравнений лежит:
· Аппроксимация нелинейных функций полиномиальными;
· Задание начального значения решения (приближения);
· Нахождение новых приближений к решению путём многократного использования алгоритма поиска решения.
Итерационные методы характеризуются:
· Величиной методической ошибки;
· Условиями сходимости к решению;
· Скоростью сходимости к решению.
К сожалению, не каждый метод гарантирует сходимость. Как правило, вероятность сходимости растёт, если начальное приближение оказывается близким к решению; поэтому, в ряде случаев, рекомендуется вначале применять алгоритмы, пусть и медленные, но гарантирующие сходимость (глобально сходящиеся), а затем заменять их алгоритмами, имеющими высокую скорость сходимости. К числу первых относятся, в частности, алгоритмы методов дихотомии, к числу вторых – методы Ньютона-Рафсона.
Формулы ряда методов можно получить следующим образом:
Пустьf(x)=0, тогдаK(x)⸱f(x)=0 иx=x+K(x)⸱f(x).
Здесь K(x) – произвольная неособенная (невырожденная) матрица.
Преобразуем последнюю формулу к виду
 .
.
Равенство приближённо выполняется, если ||f(xi)|| ≤ε1 и ||xi+1–xi|| ≤ε2.
В этом случае решение лежит в окрестностиxi.
Различные подходы к выбору матрицыK(x) приводят к различным методам. Наиболее известны: Метод деления отрезка пополам, метод простых итераций(метод Якоби), метод Гаусса-Зейделя, метод последовательной верхней релаксации, метод касательных (Ньютона-Рафсона)иего модификации.
ЕслиK(x)=J-1(x),где J(x) – матрица Якоби: 
получимитерационную формулу метода Ньютона-Рафсона:
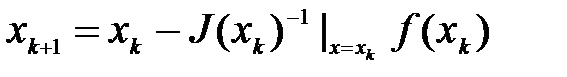 .
.
Метод Ньютона широко применяется на практике, поэтому рассмотрим его более подробно. Известно, что всякую функцию f(x) в окрестности решения можно разложить в ряд Тейлора. В этом случае
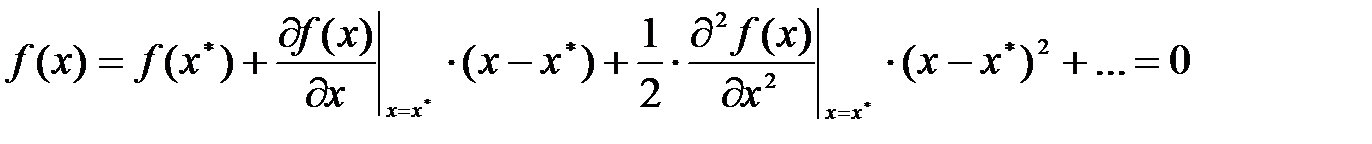 ,
,
где x=x*– решение.
Если в окрестности решения ограничиться двумя первыми членами разложения, то
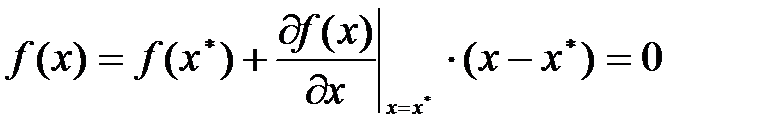
Метод Ньютона имеет квадратичную сходимость в окрестности решения.
Пример квадратичной сходимости: Пусть на k-ой итерации погрешность решения: 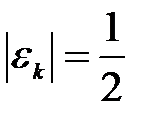 .Тогда
.Тогда
 ,
, 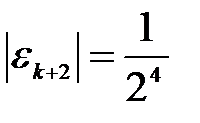 ,
,  ,
,  .
.
Итерационные методы решения систем нелинейных уравнений в конечном итоге сводятся к решению систем линейных уравнений вида Ax=B на каждой итерации.
8.6. Методы решения систем линейных уравнений (СЛАУ)
Методы делятся на прямые («точные») методы и итерационные.
Точные» методы
Приведём определение «точного» метода:
Метод решения системы уравнений относится к классу «точных», если в предположении отсутствия ошибок округления он дает точное решение задачи после конечного числа арифметических и логических операций.
Известно множество способов решения систем линейных уравнений, относящихся к классу «точных», таких как метод Гаусса, LU-факторизация, метод Краута, метод Крамера и др. На практике чаще всего используется метод Гаусса (метод последовательного исключения неизвестных).
Методы рекомендуется применять при решении СЛАУ небольшой и средней размерности. Это связано с большим числом арифметических операций, требуемых для вычислений. Так, если при представлении математической модели в матричной форме модель не разреженная и имеет порядок N*N, то число необходимых операций при решении будет, по меньшей мере, пропорционально N*N*N.
8.6.2. Итерационные методы
Применение итерационных методов в ряде случаев позволяет понизить общее число математических операций по сравнению с точными методами. Кроме того, методы итераций могут оказаться предпочтительней с точки зрения устойчивости вычислений в смысле влияния вычислительных погрешностей на результаты расчётов.
8.6.2.1Метод простых итераций
Итерационные формулы метода

Тогда

И т.д. Здесь k- номер итерации
8.6.2.2. Метод Гаусса-Зейделя (метод последовательных замещений)
Итерационные формулы метода Гаусса-Зейделя:

Недостатком метода простых итераций и метода Гаусса-Зейделя является низкая скорость сходимости.
Лекция 9
Классификация цифровых схем
– Ты что, не знаешь, что такое «это»?
– Я прекрасно знаю, что такое «это»,
когда я его нахожу.
Льюис Кэрролл, «Алиса в Стране чудес»
Цифровые схемы (ЦС) делят на комбинационные и последовательностные.
ПустьX–множество двоичных переменных на входах (x1, …, xn),аY– множество двоичных переменных на выходах (y1, …, yk).
Если значенияYв течение каждого такта определяются только значениямиXв этом же такте, то ЦС называется комбинационной. Такая схема состоит из логических элементов. Если значенияYопределяются значениямиX, как в течение рассматриваемого такта, так и существовавшими в ряде предыдущих тактов, то ЦС называется последовательностной. В последовательностной схеме кроме логических должны быть еще и запоминающие элементы.
Структура последовательностного и комбинационного устройства приведена на рис.9.1.
Поскольку запоминающее устройство может хранить информацию не бесконечно большого, а только ограниченного числа тактов, то ЦС с памятью называют конечными автоматами, к которым относят все ЭВМ.
Комбинационным устройством является, в частности, мультиплексор. Мультиплексор обеспечивает передачу в желаемом порядке цифровой информации, поступающей по нескольким входам на один выход.
К устройствам последовательностного типа относятся триггеры, регистры, счётчики и т.д.

Рис.9.1. Структура комбинационного и последовательностного цифровых устройств
Таблицы, показывающие взаимосвязь между входными и выходными переменными комбинационных устройств, называют таблицами истинности.
Алгебраическая форма этих связей представляет систему уравнений:

В общем виде в последовательностных устройствах выходные переменныеyiзависят не только от входных сигналовxm, но и от сигналов элементов памяти, поступающих за этот же такт. Для описания работы последовательностных устройств используются таблицы переходов состояний.
Таблицы истинности соответствуют только статическим или установившимся режимам работы цифровых устройств. При изменении входных сигналов в комбинационной схеме из-за инерционности логических элементов в ней начинает протекать переходный процесс. Максимальная длительность переходного процесса определяется максимальным числом последовательно включенных ЛЭ. Входные сигналы xmизменяются не мгновенно, а в течение некоторого времениtф, т. е. сигналы имеют фронты конечной длительности. В течение этого времени входные сигналы имеют неопределенное значение. По этой причине, а также из-за задержек сигналов в ЛЭ выходные сигналы комбинационной схемы в течение переходного процесса могут принимать значения, не соответствующие описывающим их функциям. Это явление называют переходными состояниями или “гонками”. Появление кратковременных ложных значений выходных сигналов комбинационной схемы может привести к неправильному срабатыванию других схем, подключенных к ее выходам.
Цифровые устройства можно разделить на асинхронные и синхронные. В асинхронных изменение входных сигналов сразу же вызывает изменение выходных сигналов. В синхронных изменение выходных сигналов, соответствующее новому сочетанию входных, происходит только после подачи синхронизирующих (тактовых) импульсов, управляющих работой автомата. Период синхроимпульсов является, таким образом, минимальным временем между выполнением автоматом двух последовательных микроопераций, т.е. служит единицей машинного времени, называемой тактом. В зависимости от структуры автомата за один такт могут выполняться одна или несколько микроопераций, если они совмещены во времени.
В асинхронных устройствах отсутствуют синхронизирующие сигналы, поэтому в их структуры обычно включаются специальные схемы, которые после окончания каждой микрооперации вырабатывают сигнал готовности к выполнению следующей микрооперации.
Синхронные устройства, в принципе, имеют меньшее быстродействие, чем асинхронные, однако в них легко устраняются опасные состязания.
Логическую схему можно представлять на поведенческом, структурном, физическом уровне (см. рис.9.2).

Рис.9.2. Модели ЦС
При построении моделей ЦС рассматриваются три подхода: функциональный, структурный ипредставление языками описания аппаратуры (HDL).
9.1. Функциональные модели
Суть функционального подхода заключается в абстрагировании от внутренней организации устройства и рассмотрении только его логики функционирования. Как правило, под ЦС подразумеваются устройства, перерабатывающие двоичную информацию.
9.1.1. Модели комбинационных схем
В качестве функциональной модели комбинационных устройств, чаще всего, используют систему булевых функций. Простейшим способом представления булевой функции является таблица истинности. Кроме этих таблиц истинности часто используются также табличные модели в виде так называемых «примитивных» (простых) кубов. Эти кубы в сжатом виде фактически представляют ту же самую информацию. Один «примитивный» куб объединяет несколько «соседних» строк таблицы истинности, на которых булева функция принимает одно и тоже значение. Под «соседними» здесь понимаются строки, отличающиеся значением одного (или более) бита. В отличие от таблиц истинности такие кубы используют не двоичный, а троичный алфавит. Фактически, «примитивный» куб соответствует простой импликанте. (Импликанта функции – некоторая логическая функция, обращаемая в ноль, по крайней мере, на тех же наборах переменных, на которых сама функция также равна нулю).
9.1.2. Модели последовательностных схем
В качестве функциональной модели последовательностных устройств используется абстрактный конечный автомат, являющийся совокупностью пяти объектовA=(Y, X, Z, δ, λ), где Y, X, Z– конечные множества состояний входных и выходных сигналов соответственно; δ: Y×X→Y– функция переходов, определяющая следующее состояние автомата; λ: Y×X→Z– функция выхода, определяющая выходной сигнал.
Автоматы представляются таблицей либо графом переходов и выходов.
Следует отметить, что в этой форме представления неявно предполагается, что функционирование автомата рассматривается в дискретном времени, принимающем целые неотрицательные значенияt=0,1,2,….Такие автоматы называются синхронными.
Асинхронные последовательностные схемы не имеют входов синхронизации. Их поведение может быть также представлено таблицей переходов и выходов. Но, в отличие от предыдущего случая, здесь изменение входного сигнала может вызвать цепочку переходов состояний, пока не будет достигнуто стабильное состояние.
Лекция 10
Логическое проектирование
Убить Время!
Разве такое ему может понравиться!
Если бы ты с ним не ссорилась,
могла бы просить у него всё, что хочешь.
Льюис Кэрролл, «Алиса в Стране чудес»
Этап логического проектирования предшествует разработке принципиальной электрической схемы и её топологии. На этапе логического проектирования необходимо решать следующие взаимосвязанные задачи: логический синтез, логическое моделирование БИС на уровне логических элементов (ЛЭ), синтез контролирующих и диагностических тестов. Задачей логического синтеза, например, функционального узла ЭВМ, является выбор базиса ЛЭ для построения различных БИС и соединение их между собой так, чтобы осуществлялось заданное функционирование. При этом надо учитывать особенности выбранных ЛЭ и их технической реализации, т.е. учитывать схемотехнику, топологические и технологические ограничения (принцип итерационности проектирования). Синтез логических схем может производиться как автоматически по структурной схеме (или по описанию поведения схемы) в заданном логическом базисе, так и вручную. В обоих случаях САПР поддерживает этот этап средствами логического проектирования.
Логическое моделирование включает в себя построение математической модели ЦС – системы соотношений, описывающей поведение исследуемой схемы с заданной точностью, и дальнейший анализ поведения этой модели на заданной последовательности входных воздействий. При решении задач анализа и диагностирования ЦС обычно используется структурная математическая модель объекта, отражающая совокупность компонентов объекта, связи между компонентами и связь объекта с внешней средой. Для выполнения логического моделирования необходимы следующие компоненты:
· Модель ЦС;
· Входные воздействия;
· Библиотека логических элементов;
· Программа моделирования;
· Результаты моделирования.
Структура системы логического моделирования представлена на рис.10.1.
Здесь внешнее описаниесхемы (графическое либо текстовое на специализированном языке) транслируется во внутреннее представление модели ЦС, которое непосредственно используется в процессе моделирования. Входные воздействия также могут быть описаны графически с помощью временных диаграмм либо текстом на специализированном языке. Важнейшей компонентой является библиотека моделей логических элементов, состав которой во многом определяет возможности системы моделирования.

Рис.10.1. Структура системы логического моделирования
С помощью программ логического моделирования в системах автоматизированного проектиро






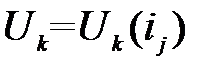

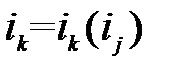



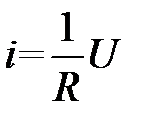 ,
,
 ,
,

 ,
,

 ,
,
 ,
,

 ,
,
 ,
,

 ,
,
 ,
,

 ,
,



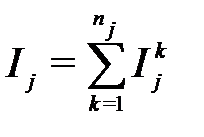 , (8.1)
, (8.1) .
. (8.2)
(8.2) – матрица узловых проводимостей (матрица Якоби).
– матрица узловых проводимостей (матрица Якоби). .
. .
.
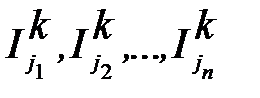 по аналитическим зависимостям, связывающим токи выводов и напряжения на выводах компонента. Например, для резистора, включенного между узлами j1иj2,
по аналитическим зависимостям, связывающим токи выводов и напряжения на выводах компонента. Например, для резистора, включенного между узлами j1иj2,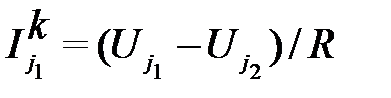 ,
,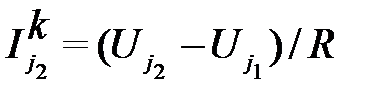 .
. .
. ,i=1,2,…,n.
,i=1,2,…,n.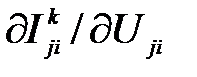 ,i,l=1,2,…,n.Для резистора эти величины равны
,i,l=1,2,…,n.Для резистора эти величины равны ,
, 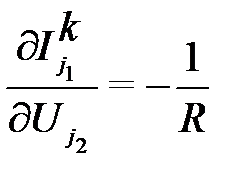 ,
,  ,
, 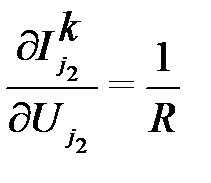 .
. , i,l=1,2,…,n.
, i,l=1,2,…,n. ;
;  ;
;  ;
; 
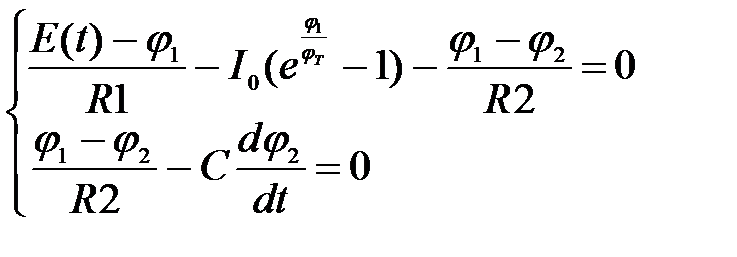
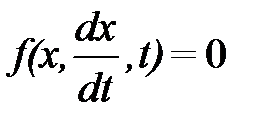 .
. ,
, подробно о методах:
подробно о методах:  системы обыкновенных дифференциальных уравнений представимы либо в общем виде, либо в форме Коши.
системы обыкновенных дифференциальных уравнений представимы либо в общем виде, либо в форме Коши.
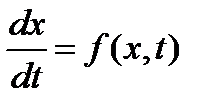
 на основании известной теоремы о среднем в интервале tn, tn+1можно заменить отношением приращенийΔx/Δt, где
на основании известной теоремы о среднем в интервале tn, tn+1можно заменить отношением приращенийΔx/Δt, где ,
,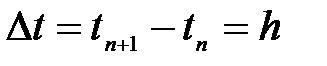 .
.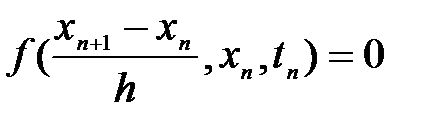




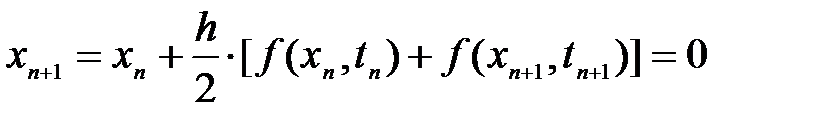
 определяется полиномом ряда Тейлора первой степени, то локальная ошибка метода определяется следующими членами полинома:
определяется полиномом ряда Тейлора первой степени, то локальная ошибка метода определяется следующими членами полинома:

 .
.
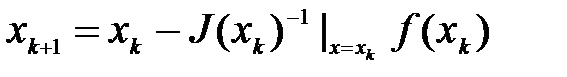 .
.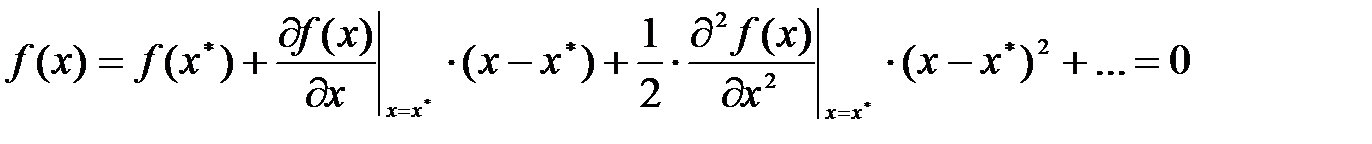 ,
,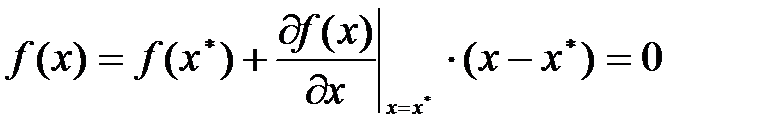
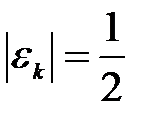 .Тогда
.Тогда ,
, 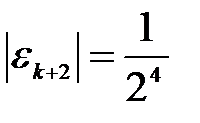 ,
,  ,
,  .
.






