Задание:
1) Вычислить интеграл методом левых и правых прямоугольников при n=10, оценивая точность с помощью сравнения полученных результатов.
2) Вычислить интеграл по формуле средних прямоугольников используя для оценки точности двойной просчет при n 1=S, n 2=10.
Теоретическая часть.
Вычисление определенного интеграла исторически обусловлено задачей расчета площадей различных фигур. Согласно “теореме о среднем” определенный интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке "x i " этого отрезка:
f ( 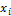 )
)
a 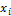 b
b
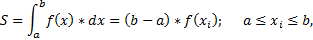
,где a и b - верхний и нижний пределы интегрирования.
Таким образом, определённый интеграл равен площади прямоугольника с основанием длиной 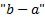 и высотой
и высотой 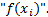 Здесь значение
Здесь значение 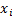 , а значит и
, а значит и 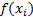 неизвестно. Однако, если отрезок интегрирования разбить на много малых отрезков
неизвестно. Однако, если отрезок интегрирования разбить на много малых отрезков 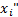 , в которых значение функции
, в которых значение функции 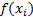 можно принять постоянным, то
можно принять постоянным, то
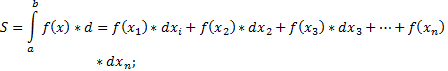
где 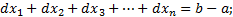
Вычисление определенного интеграла по приведенной выше формуле называется численным интегрированием. Численное интегрирование применяют при решении различных задач, например: при определении площадей сложных геометрических фигур, определении работы сил, расчете длины траектории точки и в других случаях, когда подынтегральная функция "f(x)"задана по точкам, имеет сложное аналитическое выражение или ее первообразная не определяется аналитически. Сущность численных методов интегрирования состоит в различной замене (интерполяции) сложной подынтегральной функции на малых отрезках простой функцией, либо в представлении подынтегральной функции в виде сходящегося бесконечного ряда.
Рассмотрим методы численного интегрирования, основанные на интерполяции подынтегральной функции на малых отрезках равной длины различными видами функций: постоянной, линейной, квадратичной и кубической. Формулы численного интегрирования, получаемые при различных интерполяциях подынтегральной функции, называются квадратурными.
При равномерном разбиении отрезка [a, b] на “N” малых отрезков (интервалов) необходимо определять значения функции 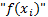 в “M” точках внутри отрезка [a, b].
в “M” точках внутри отрезка [a, b].
Метод прямоугольников основан на интерполяции функции на малом отрезке постоянным значением. Кривую 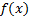 на каждом малом интервале “h” заменяют горизонтальной линией, пересекающей кривую в середине отрезка, при этом M=N. Интеграл вычисляется по формуле:
на каждом малом интервале “h” заменяют горизонтальной линией, пересекающей кривую в середине отрезка, при этом M=N. Интеграл вычисляется по формуле:
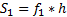 ; - на одном отрезке.
; - на одном отрезке.
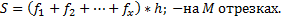
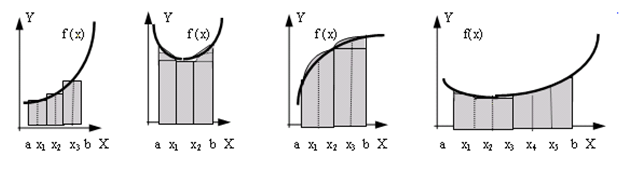 Здесь
Здесь 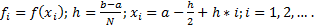
Метод трапеций состоит в том, что кривую f(x) на каждом малом интервале "h" заменяют отрезком прямой, соединяющим точки кривой f(x) на краях этого интервала, при этом M=N - 1. Интеграл вычисляется по формуле:
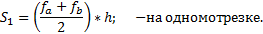
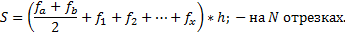
Здесь 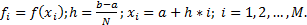
Метод Симпсона основан на интерполяции функции на малом отрезке квадратичной параболой, проходящей через крайние и среднюю точки кривой f(x). При этом M=2 * N - 1, а интеграл вычисляется по формуле:
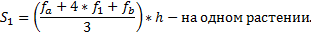
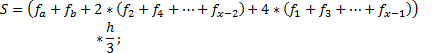
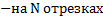 .
.
Здесь 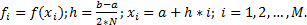
Варианты заданий
№1. 1) 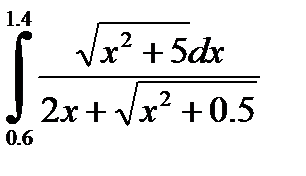 2)
2) 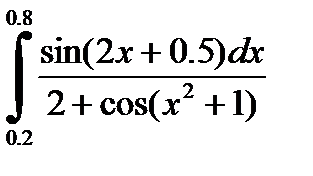
№2. 1) 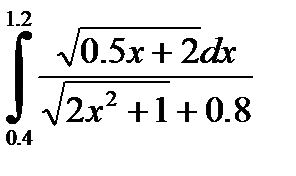 2)
2) 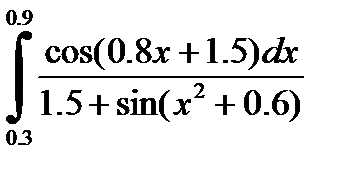
№3. 1) 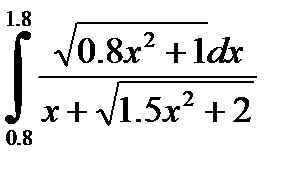 2)
2) 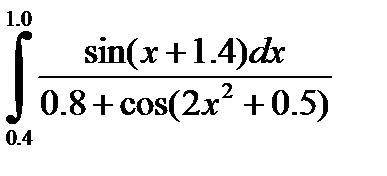
№4. 1) 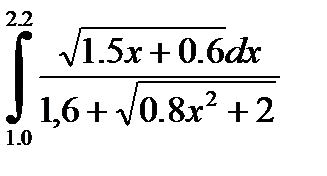 2)
2) 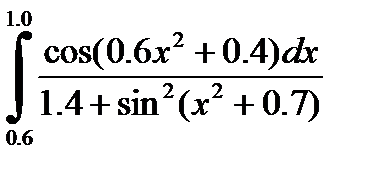
№5. 1) 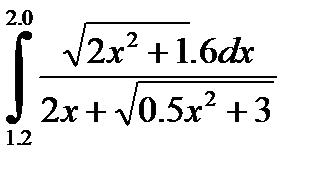 2)
2) 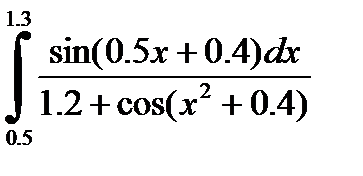
№6. 1) 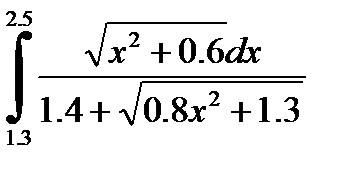 2)
2) 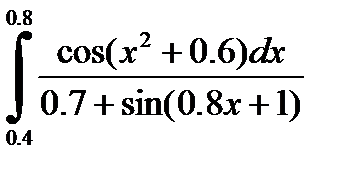
№7. 1) 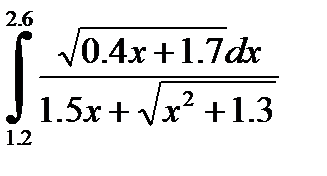 2)
2) 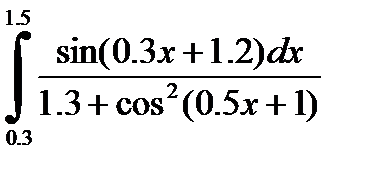
№8. 1) 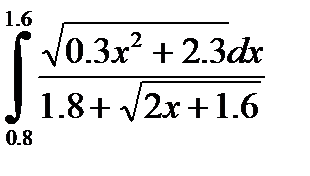 2)
2) 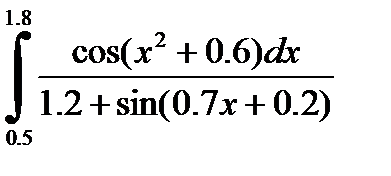
№9. 1) 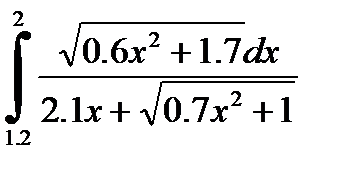 2)
2) 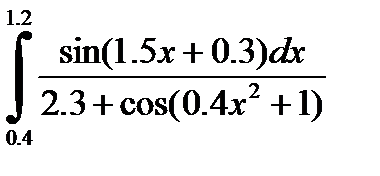
№10. 1) 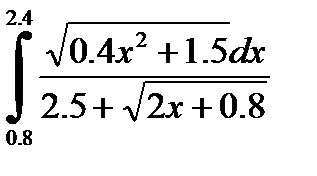 2)
2) 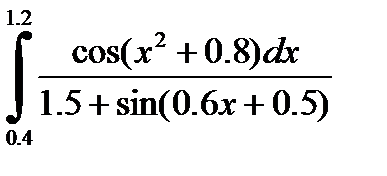
№11. 1) 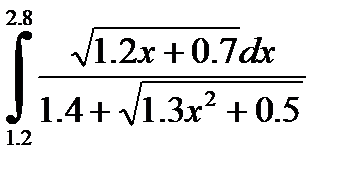 2)
2) 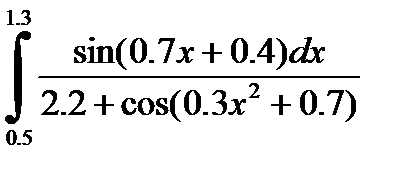
№12. 1) 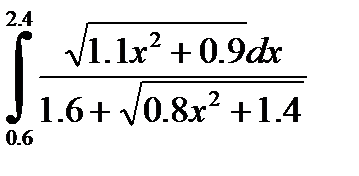 2)
2) 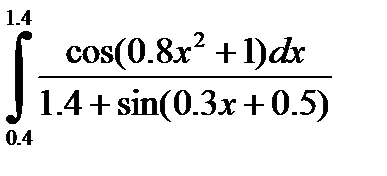
№13. 1) 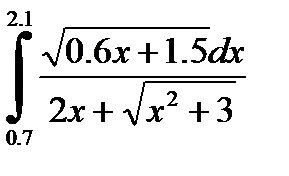 2)
2) 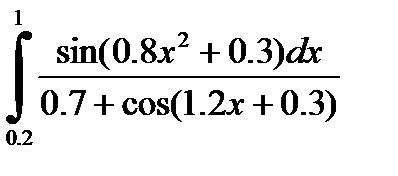
№14. 1) 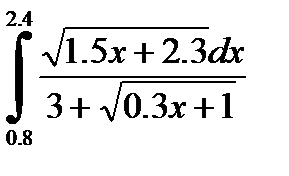 2)
2) 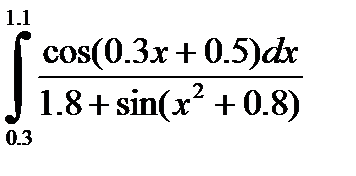
№15. 1) 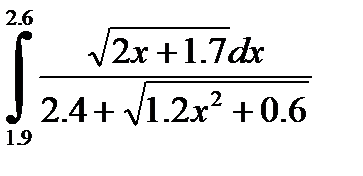 2)
2) 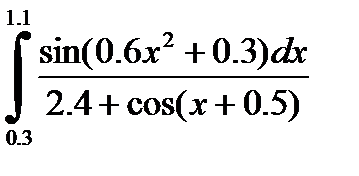
№16. 1) 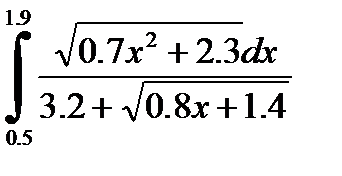 2)
2) 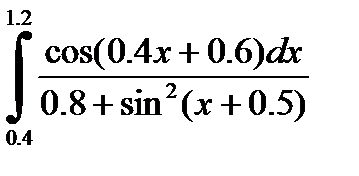
№17. 1) 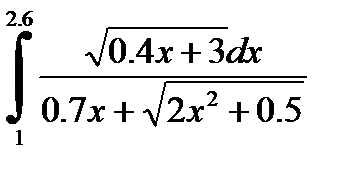 2)
2) 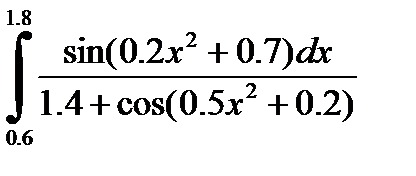
№18. 1) 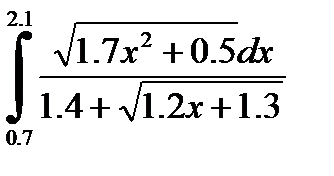 2)
2) 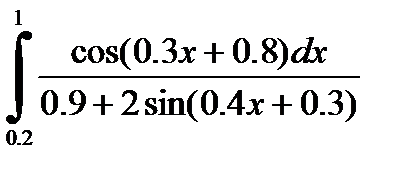
№19. 1)  2)
2) 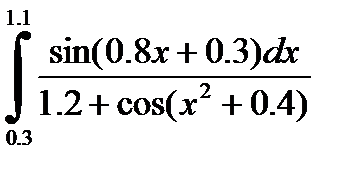
№20. 1) 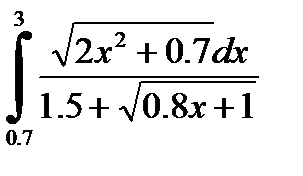 2)
2) 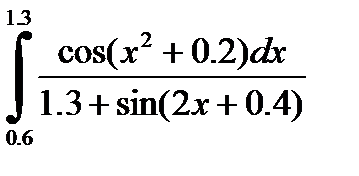
№21. 1) 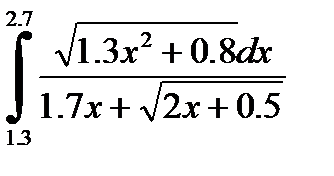 2)
2) 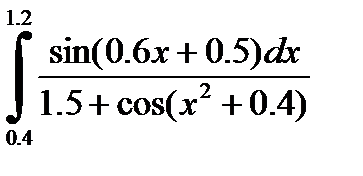
№22. 1) 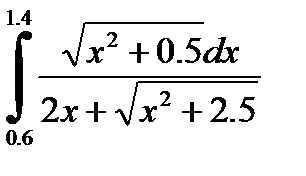 2)
2) 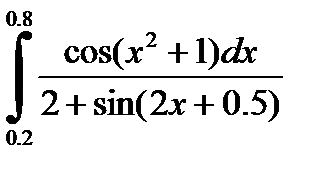
№23. 1) 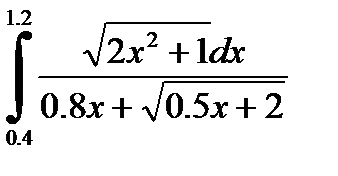 2)
2) 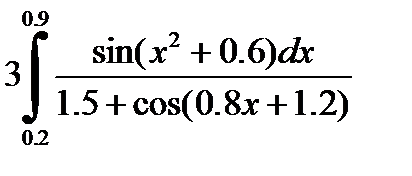
№24. 1) 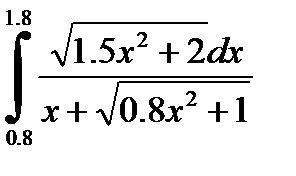 2)
2) 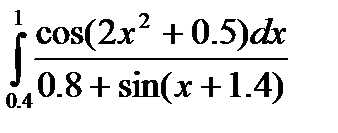
№25. 1) 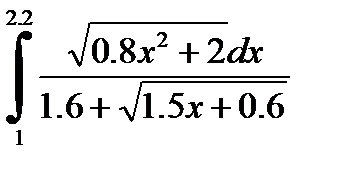 2)
2) 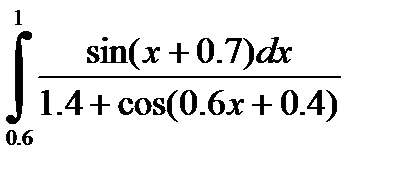
№26. 1) 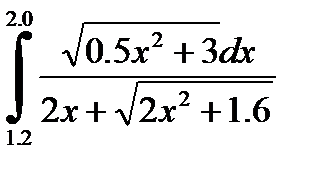 2)
2) 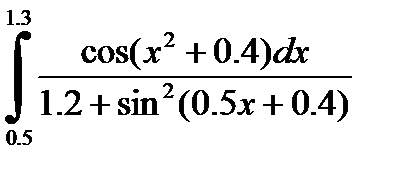
№27. 1) 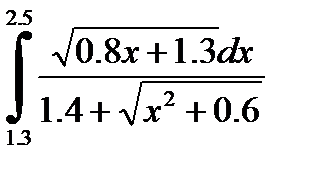 2)
2) 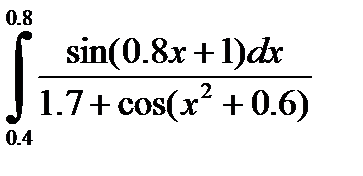
№28. 1) 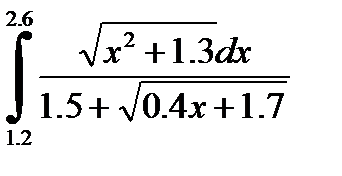 2)
2) 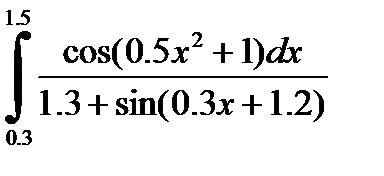
№29. 1) 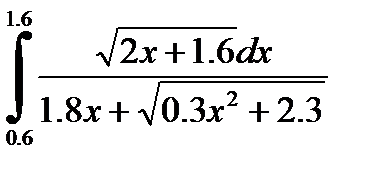 2)
2) 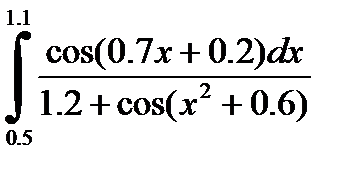
№30. 1) 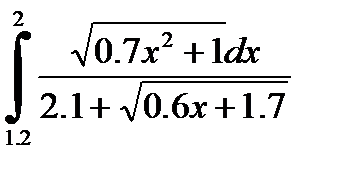 2)
2) 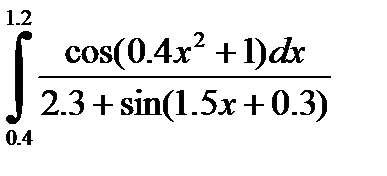
Образец выполнения задания.
№1. 1) 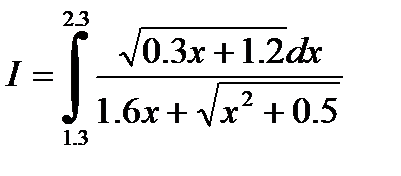 2)
2) 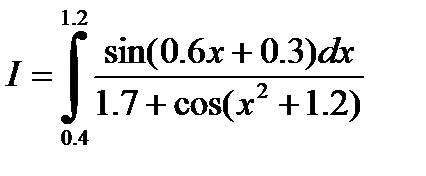
Пример вычисления интегралов методом левых и правых прямоугольников
Для вычислений по формулам левых и правых прямоугольников при n =10 разобьем отрезок интегрирования на 10 частей с шагом
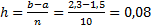 .
.
Составим таблицу значений подынтегральной функции в точках деления отрезка (см. таб. 4):
Таблица 4
| i
| xi
| 0,3xi+1,2
| 
| 
| 1,6xi+ 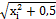
| yi
|
|
| 1,5
1,58
1,66
1,74
1,82
1,90
1,98
2,06
2,14
2,22
2,30
| 1,65
1,674
1,698
1,722
1,746
1,77
1,794
1,818
1,842
1,866
1,89
| 1,2845
1,2938
1,3031
1,3122
1,3214
1,3304
1,3394
1,3483
1,3572
1,3660
1,3748
| 1,6583
1,7310
1,8043
1,8782
1,9525
2,0273
2,1025
2,1780
2,2538
2,3299
2,4062
| 4,0583
4,2590
4,4603
4,6622
4,8545
5,0673
5,2705
5,4740
5,6778
5,8819
6,0862
| 0,3165
0,3037
0,2922
0,2815
0,2716
0,2626
0,2541
0,2463
0,2390
0,2322
0,2259
|
| | 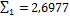
|
| | 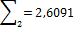
|
В таблице найдены значения сумм: 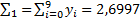 ;
; 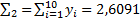 .
.
Найдем приближенные значения интеграла. По формуле левых прямоугольников получим
I1=h 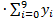 = 0,08
= 0,08  2,6997 = 0,2158.
2,6997 = 0,2158.
По формуле правых прямоугольников находим
I2=h 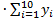 = 0,08
= 0,08  2,6091 = 0,2087.
2,6091 = 0,2087.
Эти результаты отличаются уже в сотых долях. За окончательное значение примем полусумму найденных значений, округлив результат до тысячных:
I= 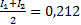 .
.
Пример вычисления интегралов методом средних прямоугольников
Для решения воспользуемся формулой средних прямоугольников:
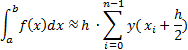
Вычисления выполним дважды при n1=8 и при n2=10 и соответственно при h1=(b - a)/n1 = (1,2 - 0,4)/8 = 0,1 и h2=(b - a)/n2 = (1,2 - 0,4)/10 = 0,08. Результаты вычислений приведены в таблицах 5 и 6
Таблица 5
| i
| xi
| xi+ 
| sin(0,6х+0,3)
| 1,7+cos(x2+1.2)
| y(xi+  ) )
|
|
| 0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
| 0,45
0,55
0,65
0,75
0,85
0,95
1,05
1,15
| 0,53963
0,58914
0,63654
0,68164
0,72429
0,76433
0,80162
0,83603
| 1,86750
1,76824
1,64832
1,05947
1,35550
1,19300
1,03186
0,88559
| 0,28896
0,33318
0,38618
0,45158
0,53433
0,64068
0,77687
0,94404
|
| | 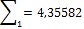
|
Таблица 6
| i
| xi
| xi+ 
| sin(0,6х+0,3)
| 1,7+cos(x2+1.2)
| y(xi+  ) )
|
|
| 0,4
0,48
0,56
0,64
0,72
0,80
0,88
0,96
1,04
1,12
| 0,44
0,52
0,60
0,68
0,76
0,84
0,92
1,00
1,08
1,16
| 0,53457
0,57451
0,61312
0,65032
0,68602
0,72014
0,75260
0,78333
0,81225
0,83930
| 1,87627
1,80022
1,71080
1,60852
1,49467
1,37142
1,24212
1,11150
0,98571
0,87241
| 0,28491
0,31913
0,35838
0,40430
0,45898
0,52511
0,60590
0,70475
0,82403
0,96205
|
| | 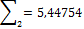
|
Найдем приближенные значения интеграла
I1 = h1 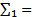 0,1
0,1  4,35582 = 0,43558;
4,35582 = 0,43558;
I2 = h2 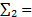 0,08
0,08  5,44754 = 0,43580.
5,44754 = 0,43580.
Значения различаются в десятичных долях, но второе значение точнее первого, поэтому принимаем I 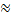 0,4358.
0,4358.
Контрольные вопросы
1. Объяснить уменьшение погрешности нахождения интеграла в методе прямоугольников.
2. Объяснить в каких случаях находит применение метод треугольника.
3. Обосновать возможность получения методом прямоугольников точного значение интеграла.
4. Объяснить влияние на точность интегрирования величины шага
h.
5. Приведите шаблон формулы метода прямоугольников и саму формулу.
Лабораторная работа 4



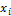 )
)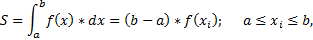
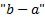 и высотой
и высотой 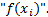 Здесь значение
Здесь значение 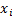 , а значит и
, а значит и 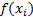 неизвестно. Однако, если отрезок интегрирования разбить на много малых отрезков
неизвестно. Однако, если отрезок интегрирования разбить на много малых отрезков 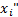 , в которых значение функции
, в которых значение функции 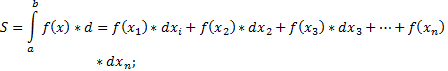
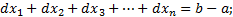
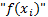 в “M” точках внутри отрезка [a, b].
в “M” точках внутри отрезка [a, b].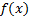 на каждом малом интервале “h” заменяют горизонтальной линией, пересекающей кривую в середине отрезка, при этом M=N. Интеграл вычисляется по формуле:
на каждом малом интервале “h” заменяют горизонтальной линией, пересекающей кривую в середине отрезка, при этом M=N. Интеграл вычисляется по формуле: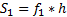 ; - на одном отрезке.
; - на одном отрезке.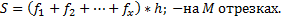
 Здесь
Здесь 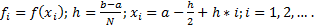
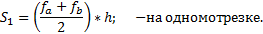
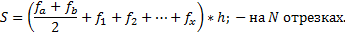
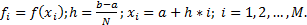
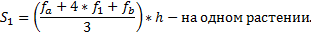
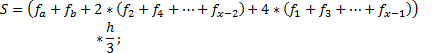
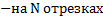 .
.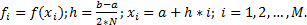
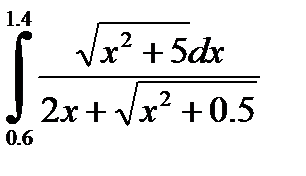 2)
2) 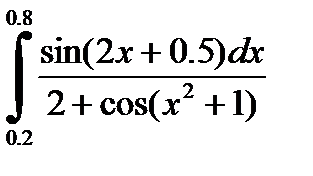
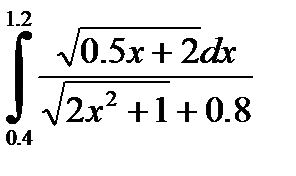 2)
2) 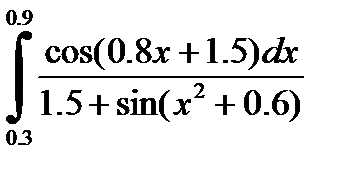
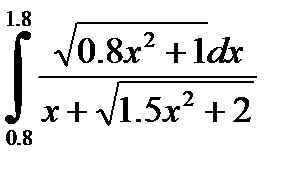 2)
2) 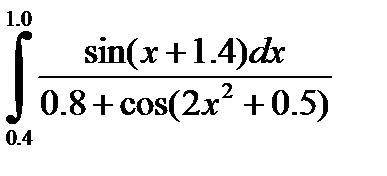
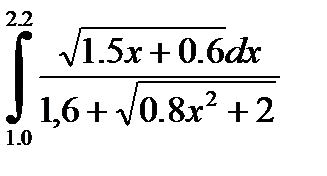 2)
2) 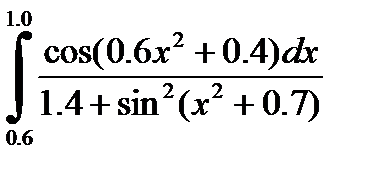
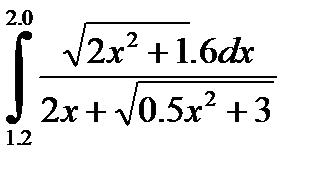 2)
2) 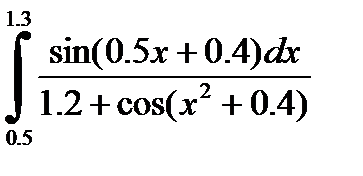
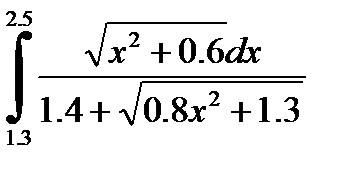 2)
2) 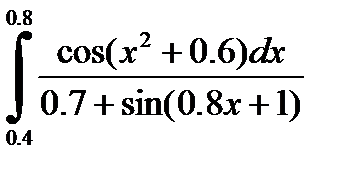
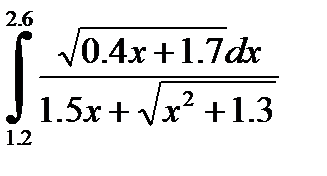 2)
2) 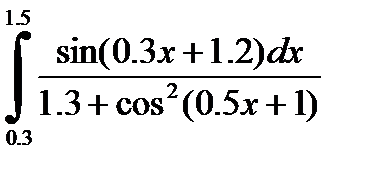
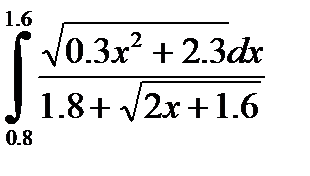 2)
2) 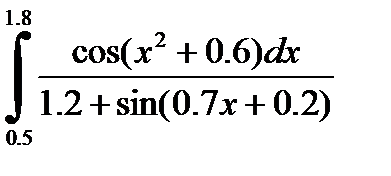
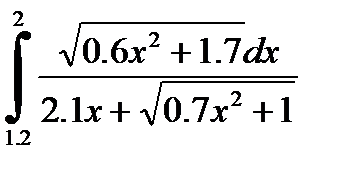 2)
2) 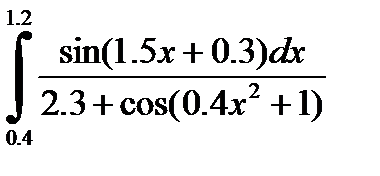
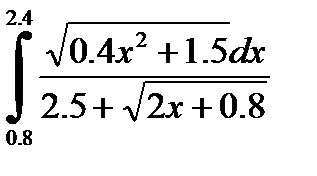 2)
2) 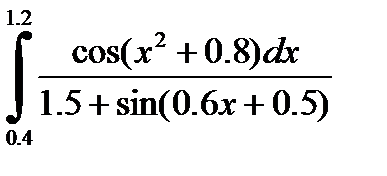
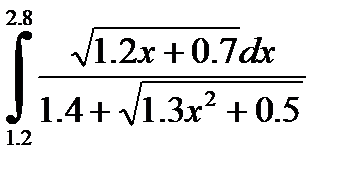 2)
2) 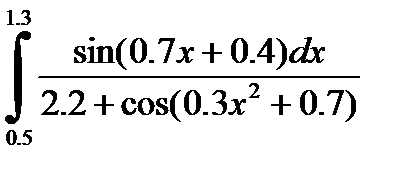
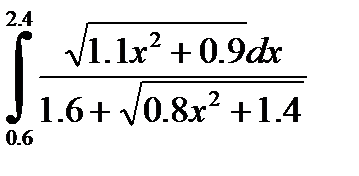 2)
2) 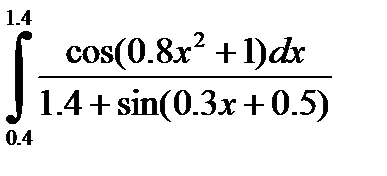
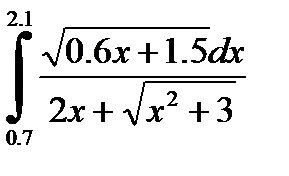 2)
2) 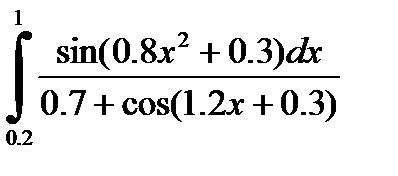
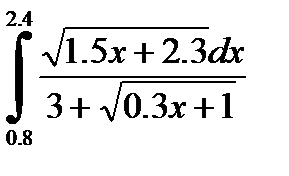 2)
2) 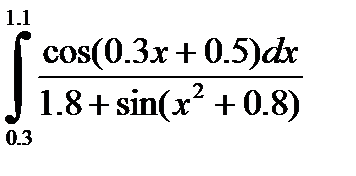
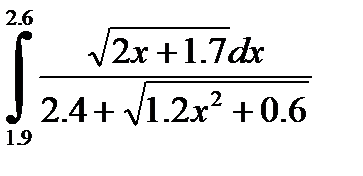 2)
2) 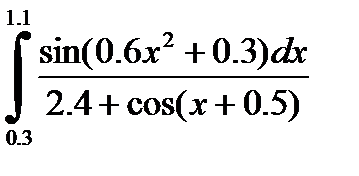
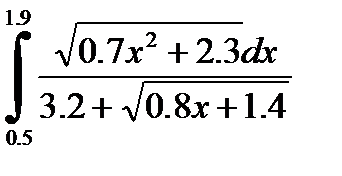 2)
2) 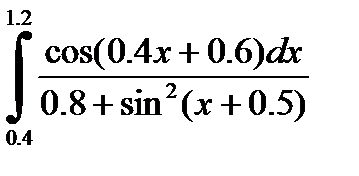
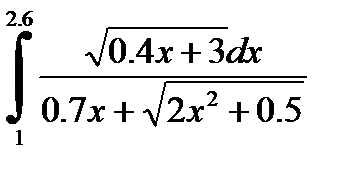 2)
2) 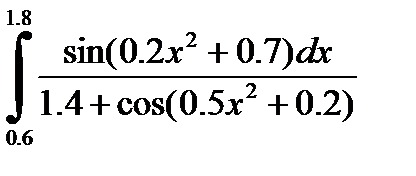
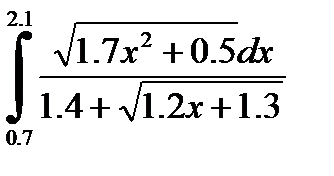 2)
2) 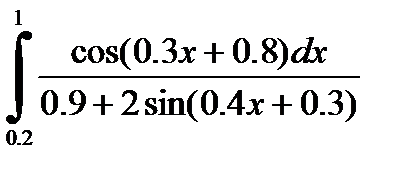
 2)
2) 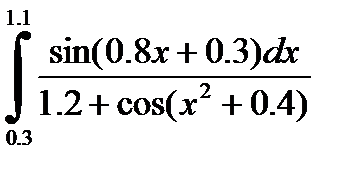
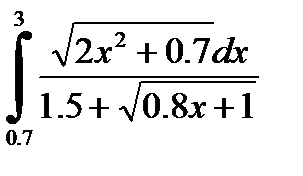 2)
2) 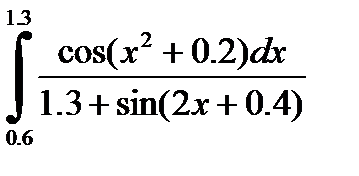
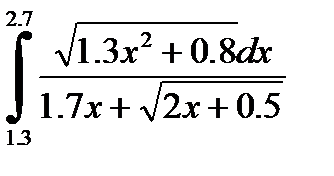 2)
2) 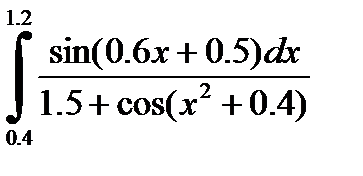
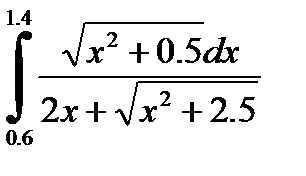 2)
2) 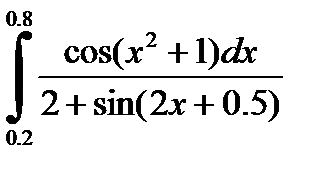
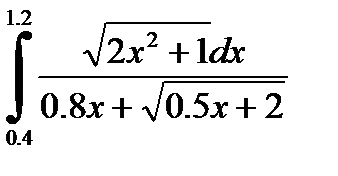 2)
2) 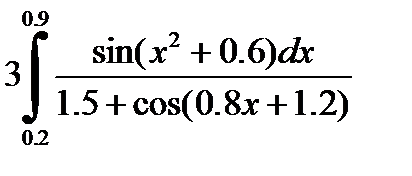
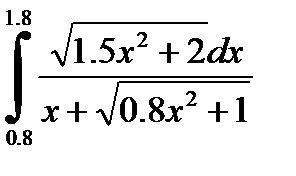 2)
2) 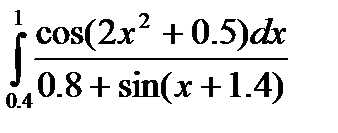
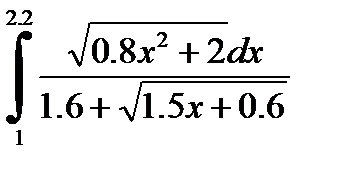 2)
2) 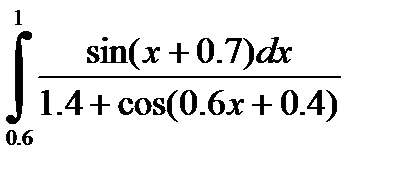
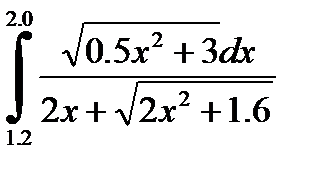 2)
2) 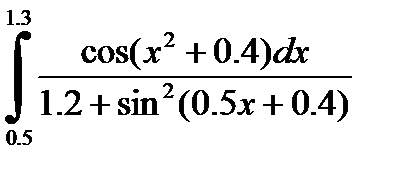
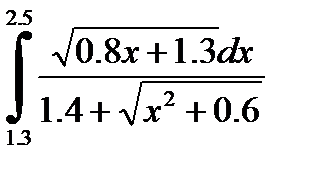 2)
2) 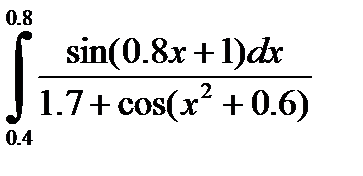
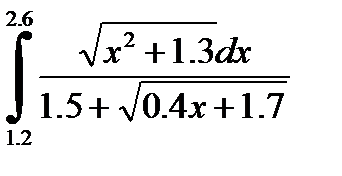 2)
2) 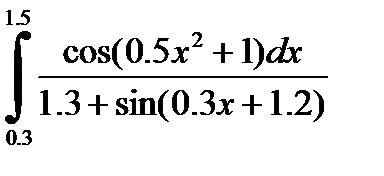
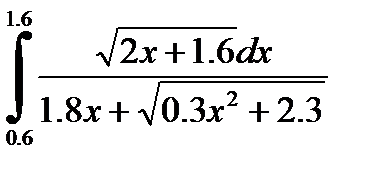 2)
2) 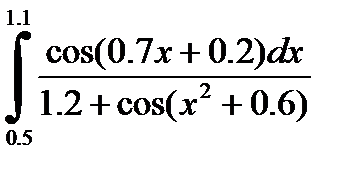
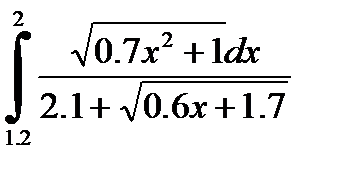 2)
2) 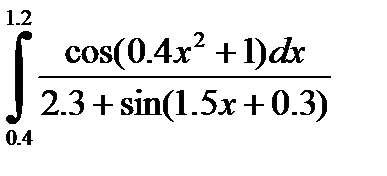
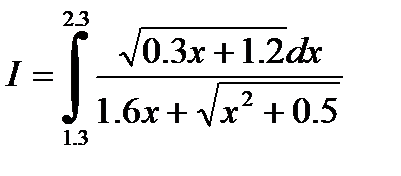 2)
2) 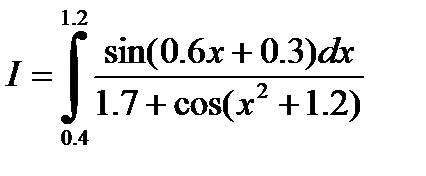
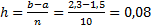 .
.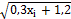
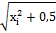
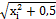
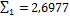
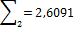
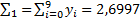 ;
; 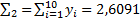 .
.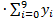 = 0,08
= 0,08  2,6997 = 0,2158.
2,6997 = 0,2158.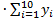 = 0,08
= 0,08 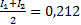 .
.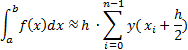

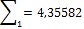
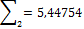
 0,1
0,1  4,35582 = 0,43558;
4,35582 = 0,43558; 0,08
0,08  0,4358.
0,4358.


