Как уже отмечалось выше, определение потенциала в некоторой области пространства является достаточно общей задачей в прикладной математики и физике. В такой задаче потенциал должен удовлетворять уравнению Пуассона

 (96)
(96)
при выполнении условий на границе области s
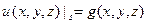 (97)
(97)
Однако в декартовой системе координат функция g для любой криволинейной области будет функцией всех трех координат. Это не только неудобно, но и не позволяет применить некоторые методы решения задачи, как это уже было с методом разделения переменных. В связи с этим целесообразно выбрать такую систему координат, чтобы граница области совпадала с одной из координатной линий. Так например, для решения задачи Дирихле в единичном круге целесообразно выбрать на плоскости полярную систему координат. Тогда, задача будет формулироваться следующим образом:
Требуется найти решение уравнения Пуассона, записанного в полярной системе координат (r, θ)
 (98)
(98)
c граничным условием
 (99)
(99)
Для большей наглядности метода решения здесь выбраны нулевые граничные условия. Вклад неоднородных граничных условий можно будет найти по интегральной формуле Пуассона для уравнения Лапласа из предыдущего параграфа.
Сначала определим потенциал, который создает точечный источник (электрический или тепловой) с мощностью q на расстоянии r. С этой целью запишем поток из окружности радиуса r, который должен быть равен мощности источника q, т.е.
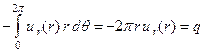
Решая это дифференциальное уравнение, мы получим
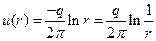 (100)
(100)
Теперь поместим единичный точечный заряд в некоторую точку единичного круга с координатами (ρ, φ), тогда в любой точке круга с координатами (r, θ) (Рис. 29) будет создавать потенциал, равный
 ,
,
где R – расстояние от точки (ρ, φ) до точки (r, θ). Этот потенциал равен нулю на расстоянии R = 1, но на границе круга он, конечно не равен единице, как того требует граничное условие задачи.

Чтобы искомый потенциал удовлетворял граничному условию применим так называемый метод изображений. Поместим снаружи круга (см. Рис. 29) противоположный единичный заряд так, чтобы суммарный потенциал этих двух зарядов на окружности r =1 был бы постоянной величиной. Можно убедиться, что эта цель будет достигнута, если противоположный заряд поместить в точку с координатами (1/ ρ, φ). Действительно, в этом случае суммарный потенциал будет равен
 ,
,
где 
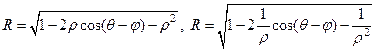
Если мы теперь вычтем из суммарного потенциала  величину
величину  , то потенциал
, то потенциал  на границе будет равен нулю.
на границе будет равен нулю.
Функцию  называют функцией единичного источника для неоднородной задачи Дирихле или функцией Грина. Она является решением задачи Дирихле, если внутри круга помещен одиночный единичный заряд. Для определения потенциала, создаваемого распределенным по кругу зарядом с плотностью f (r, φ), то нужно функцию единичного источника
называют функцией единичного источника для неоднородной задачи Дирихле или функцией Грина. Она является решением задачи Дирихле, если внутри круга помещен одиночный единичный заряд. Для определения потенциала, создаваемого распределенным по кругу зарядом с плотностью f (r, φ), то нужно функцию единичного источника  умножить на эту плотность и проинтегрировать по всей площади единичного круга. Тогда окончательное решение задачи будет иметь вид
умножить на эту плотность и проинтегрировать по всей площади единичного круга. Тогда окончательное решение задачи будет иметь вид
 (101)
(101)
Г л а в а VI. Теория потенциала
Теория потенциала является одной из наиболее ранних областей математической физики и важной с точки зрения приложения к физическим задачам. Эта теория базируется на том, что функция

представляет собой потенциал поля единичной массы (или зарада), помещенной в точке M 0(ξ, η, ζ). Эта функция является решением уравнения Лапласа, которое зависит от координат точки M 0 как от параметров. Обратимся тепеть к понятию объемного потенциала.
Объемный потенциал
Пусть в некоторой точке M 0 помещена масса m 0. По закону всемирного тяготения на массу m, помещенную в точке M (x,y,z), действует сила притяжения
 , (1)
, (1)
где r – радиус-вектор в направлении  , а g – гравитационная постоянная. Выбирая систему единиц так, чтобы g = 1, и полагая m = 1, получим
, а g – гравитационная постоянная. Выбирая систему единиц так, чтобы g = 1, и полагая m = 1, получим
 (2)
(2)
Для векторной функции F существует такая скалярная функция U, называемая потенциалом силового поля, что выполняется соотношение
 , (3)
, (3)
где
 (4)
(4)
В том случае, когда масса непрерывно распределена с плотностью r (x, h,z) по некоторому телу объемом V, где x, h,z – координаты точек этого тела, то его потенциал в точке M (x, y, z) будет определяться выражением
 , (5)
, (5)
где  , а точка M лежит за пределами тела.
, а точка M лежит за пределами тела.
К аналогичному выражению мы приходим и при рассмотрении электростатического поля. По закону Кулона для среды с диэлектрической постоянной, равной единице, сила, действующая со стороны заряда q на одноименный единичный заряд, находящийся на расстоянии r, равна
 (6)
(6)
Следовательно, и для потенциала электрического заряда, непрерывно распределенного по объему V с плотностью заряда ρ с точностью до знака справедлива формула (5). Потенциал, задаваемый этой формулой, называют также ньютоновским потенциалом.




 (96)
(96)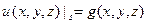 (97)
(97) (98)
(98) (99)
(99)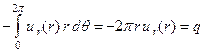
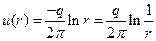 (100)
(100) ,
,
 ,
,
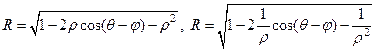
 величину
величину  , то потенциал
, то потенциал  на границе будет равен нулю.
на границе будет равен нулю. называют функцией единичного источника для неоднородной задачи Дирихле или функцией Грина. Она является решением задачи Дирихле, если внутри круга помещен одиночный единичный заряд. Для определения потенциала, создаваемого распределенным по кругу зарядом с плотностью f (r, φ), то нужно функцию единичного источника
называют функцией единичного источника для неоднородной задачи Дирихле или функцией Грина. Она является решением задачи Дирихле, если внутри круга помещен одиночный единичный заряд. Для определения потенциала, создаваемого распределенным по кругу зарядом с плотностью f (r, φ), то нужно функцию единичного источника  (101)
(101)
 , (1)
, (1) , а g – гравитационная постоянная. Выбирая систему единиц так, чтобы g = 1, и полагая m = 1, получим
, а g – гравитационная постоянная. Выбирая систему единиц так, чтобы g = 1, и полагая m = 1, получим (2)
(2) , (3)
, (3) (4)
(4) , (5)
, (5) , а точка M лежит за пределами тела.
, а точка M лежит за пределами тела. (6)
(6)


