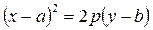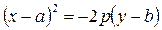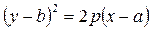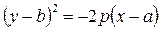1. Угол между двумя плоскостями:
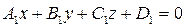 и
и 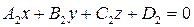 определяется по формуле:
определяется по формуле:
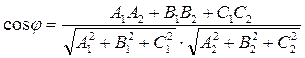 (4)
(4)
Отсюда:
Условия параллельности плоскостей:
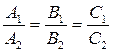 (5)
(5)
Условия перпендикулярности плоскостей:
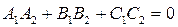 (6)
(6)
Расстояние от точки 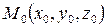 до плоскости
до плоскости 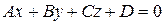 находится по формуле:
находится по формуле:
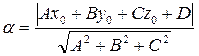 (7)
(7)
Если 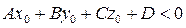 , то М 0 и О (0; 0; 0) расположены по одну сторону от плоскости.
, то М 0 и О (0; 0; 0) расположены по одну сторону от плоскости.
Если 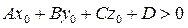 , то М 0 и О (0; 0; 0) расположены по разные стороны от плоскости.
, то М 0 и О (0; 0; 0) расположены по разные стороны от плоскости.
Прямые в пространстве
Прямая может быть задана уравнением двух плоскостей:
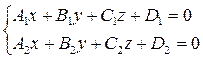 (8)
(8)
Уравнение прямой, проходящей через две точки 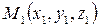 и
и 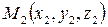
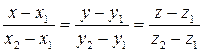 (9)
(9)
Каноническое уравнение прямой
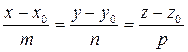 (10)
(10)
проходящей через точку 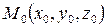 и параллельную вектору (направляющий вектор)
и параллельную вектору (направляющий вектор)
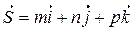 , т.е.
, т.е. 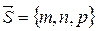
Параметрические уравнения прямой: приравняв (10) к t получим:
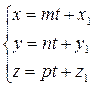 (11)
(11)
Вопросы:
1. Взаимное расположение прямой и плоскости в пространстве.
2. Кривые второго порядка.
2.1. Окружность.
2.2. Эллипс.
2.3. Гипербола.
2.4. Парабола.
Взаимное расположение прямой и плоскости в пространстве
Угол между двумя прямыми, заданными их каноническими уравнениями
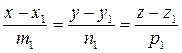 и
и 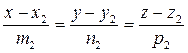 определяется по формуле:
определяется по формуле:
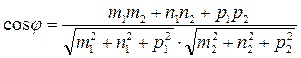 (12)
(12)
Условие параллельности двух прямых:
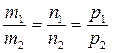 (13)
(13)
Условия перпендикулярности двух прямых:
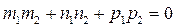 (14)
(14)
Необходимое и достаточное условие нахождения двух прямых, заданных каноническими уравнениями, в одной плоскости:
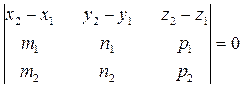 (15)
(15)
Угол между прямой 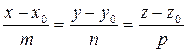 и плоскостью
и плоскостью 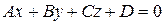 определяется по формуле:
определяется по формуле:
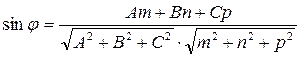
(16)
Условие параллельности плоскости и прямой:
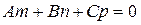 (17)
(17)
Условие перпендикулярности прямой и плоскости:
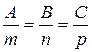 (18)
(18)
Для определения точки пересечения прямой 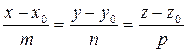 с плоскостью
с плоскостью 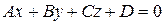 нужно решить совместно их уравнения, используя уравнение (11):
нужно решить совместно их уравнения, используя уравнение (11):
а) если 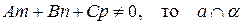
б) если 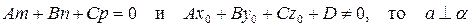
в) если 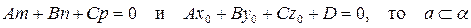
Кривые второго порядка
Окружность
Опр.: Окружностью называют геометрическое место точек, одинаково удаленных от заданной точки, называемой центром.
Обозначим центр точкой если 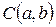 , а расстояние, на которое точки окружности удалены от центра называются радиусом: (R).
, а расстояние, на которое точки окружности удалены от центра называются радиусом: (R).
Выведем каноническое уравнение окружности:
Возьмем на окружности текущую точку 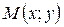 , по формуле расстояния между двумя заданными точками:
, по формуле расстояния между двумя заданными точками:
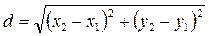
Получим: 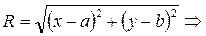
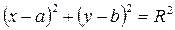 (1)
(1)
Если центр окружности находится в начале координат, то уравнение (1) упрощается: 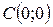
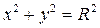 (1')
(1')
Эллипс
 Опр.: Эллипс – геометрическое место точек сумма расстояний от которых до двух заданных точек (называемых фокусами) – есть величина постоянная (равная 2 а).
Опр.: Эллипс – геометрическое место точек сумма расстояний от которых до двух заданных точек (называемых фокусами) – есть величина постоянная (равная 2 а).
Расстояние между фокусами F 1 и F 2 равно 2 с
а > c
r 1 и r 2 – фокальные радиусы
Выведем каноническое уравнение эллипса для случая, когда его фокусы лежат на оси Ox, симметрично относительно начала координат.
Возьмем на эллипсе текущую точку 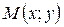 . По определения эллипса
. По определения эллипса
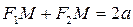
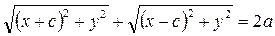
После элементарных преобразований (сделать самостоятельно), получим уравнение:
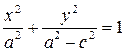
Обозначим 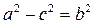 , получим:
, получим:
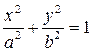 (2)
(2)
– каноническое уравнение эллипса.
Точки 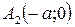 ,
, 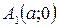 и
и 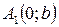 ,
, 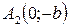 – вершины эллипса.
– вершины эллипса.
А 1 А 2 – большая ось = 2 а
В 1 В 2 – малая ось = 2 b
а – большая полуось
b – малая полуось
Показатель «выпуклости» эллипса – эксцентриситет:
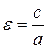
т.к. 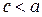 , то
, то 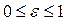
если 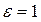 – окружность.
– окружность.
Гипербола
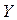

 Опр.: Гиперболой называют геометрическое место точек на плоскости, абсолютная величина разности расстояний от которых до двух заданных точек (называются фокусами) величина постоянная и равна 2 а, причем 2 а < 2 с ⇒ а < с.
Опр.: Гиперболой называют геометрическое место точек на плоскости, абсолютная величина разности расстояний от которых до двух заданных точек (называются фокусами) величина постоянная и равна 2 а, причем 2 а < 2 с ⇒ а < с.
Каноническое уравнение гиперболы аналогично эллипсу:
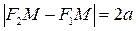
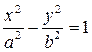 (3)
(3)
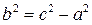
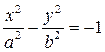 – сопряженная гипербола
– сопряженная гипербола
Гипербола строится из а и b.
Перепишем уравнение гиперболы в виде:
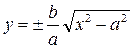
при 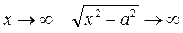 и уравнение принимает вид:
и уравнение принимает вид: 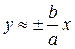
т.е. при 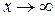 ветви гиперболы как угодно близко подходят к прямым
ветви гиперболы как угодно близко подходят к прямым
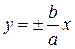 – асимптоты гиперболы.
– асимптоты гиперболы.
Оx – действительная ось гиперболы
Оy – линейная ось гиперболы
эксцентриситет 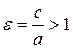 , т.к. с > 0
, т.к. с > 0
Оптические свойства:
1. Лучи света, выходящие из 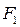 эллипса после отображения от эллипса проходят через
эллипса после отображения от эллипса проходят через 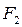 .
.
2. Лучи, исходящие из одного фокуса гиперболы после зеркального отображения – мнимый фокус 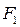 .
.
3. Лучи света из 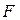 параболы после отражения образуют пучок параллельный оси параболы.
параболы после отражения образуют пучок параллельный оси параболы.
Парабола
Опр.: Параболой называется геометрическое месторасположение точек на плоскости равноудаленных от заданной точки-фокуса и заданной прямой, называемой директрисой.
Расстояние от фокуса до директрисы равно p.
Выведем каноническое уравнение параболы для случая, когда, его фокус лежит на оси Ох. ⇒ Директриса перпендикулярна оси Ох, а начало координат делит расстояние от фокуса до директрисы пополам.
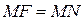
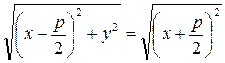
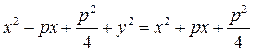
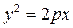 (5)
(5)
– каноническое уравнение параболы.
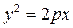 – ветви вправо, если p > 0
– ветви вправо, если p > 0
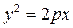 – ветви влево, если p < 0
– ветви влево, если p < 0
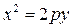 – ветви вверх, если p > 0
– ветви вверх, если p > 0
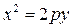 – ветви вниз, если p < 0
– ветви вниз, если p < 0
Вершина параболы может находиться в точке 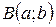 , тогда:
, тогда:
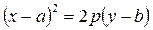
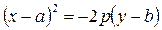
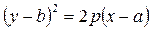
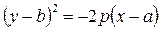
Лекция 2. ТЕОРИЯ ПРЕДЕЛОВ.
1. Предел числовой последовательности.
2. Предел функции в бесконечности и в точке.
3. Замечательные пределы.
4. Непрерывность функции Основные теоремы о пределах



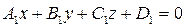 и
и 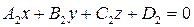 определяется по формуле:
определяется по формуле: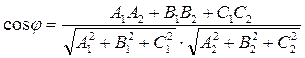 (4)
(4)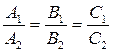 (5)
(5)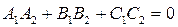 (6)
(6)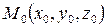 до плоскости
до плоскости 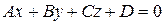 находится по формуле:
находится по формуле: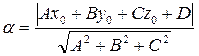 (7)
(7)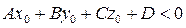 , то М 0 и О (0; 0; 0) расположены по одну сторону от плоскости.
, то М 0 и О (0; 0; 0) расположены по одну сторону от плоскости.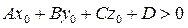 , то М 0 и О (0; 0; 0) расположены по разные стороны от плоскости.
, то М 0 и О (0; 0; 0) расположены по разные стороны от плоскости.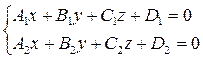 (8)
(8)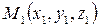 и
и 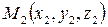
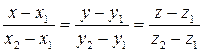 (9)
(9)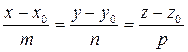 (10)
(10)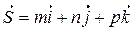 , т.е.
, т.е. 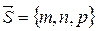
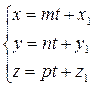 (11)
(11)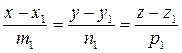 и
и 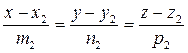 определяется по формуле:
определяется по формуле: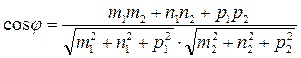 (12)
(12)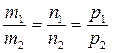 (13)
(13)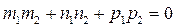 (14)
(14)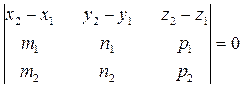 (15)
(15)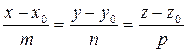 и плоскостью
и плоскостью 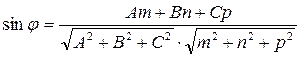
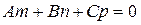 (17)
(17)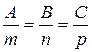 (18)
(18)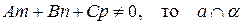
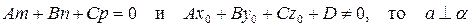
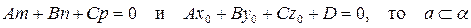
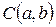 , а расстояние, на которое точки окружности удалены от центра называются радиусом: (R).
, а расстояние, на которое точки окружности удалены от центра называются радиусом: (R).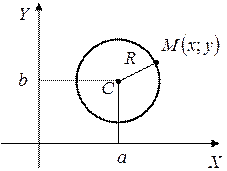
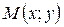 , по формуле расстояния между двумя заданными точками:
, по формуле расстояния между двумя заданными точками: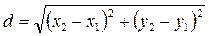
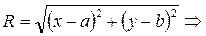
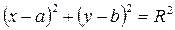 (1)
(1)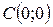
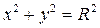 (1')
(1')
 Опр.: Эллипс – геометрическое место точек сумма расстояний от которых до двух заданных точек (называемых фокусами) – есть величина постоянная (равная 2 а).
Опр.: Эллипс – геометрическое место точек сумма расстояний от которых до двух заданных точек (называемых фокусами) – есть величина постоянная (равная 2 а).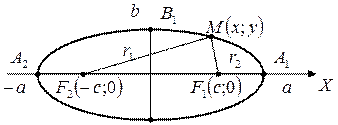
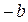
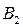
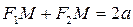
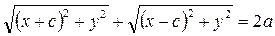
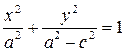
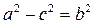 , получим:
, получим: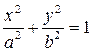 (2)
(2)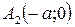 ,
, 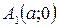 и
и 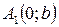 ,
, 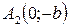 – вершины эллипса.
– вершины эллипса.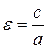
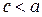 , то
, то 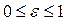
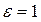 – окружность.
– окружность.
 Опр.: Гиперболой называют геометрическое место точек на плоскости, абсолютная величина разности расстояний от которых до двух заданных точек (называются фокусами) величина постоянная и равна 2 а, причем 2 а < 2 с ⇒ а < с.
Опр.: Гиперболой называют геометрическое место точек на плоскости, абсолютная величина разности расстояний от которых до двух заданных точек (называются фокусами) величина постоянная и равна 2 а, причем 2 а < 2 с ⇒ а < с.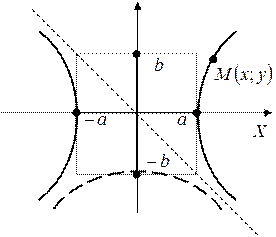
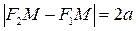
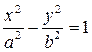 (3)
(3)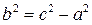
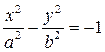 – сопряженная гипербола
– сопряженная гипербола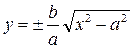
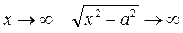 и уравнение принимает вид:
и уравнение принимает вид: 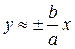
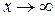 ветви гиперболы как угодно близко подходят к прямым
ветви гиперболы как угодно близко подходят к прямым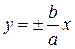 – асимптоты гиперболы.
– асимптоты гиперболы.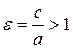 , т.к. с > 0
, т.к. с > 0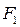 эллипса после отображения от эллипса проходят через
эллипса после отображения от эллипса проходят через 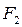 .
.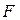 параболы после отражения образуют пучок параллельный оси параболы.
параболы после отражения образуют пучок параллельный оси параболы.
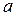
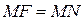
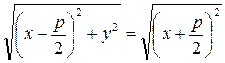
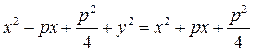
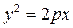 (5)
(5)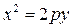 – ветви вверх, если p > 0
– ветви вверх, если p > 0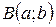 , тогда:
, тогда: