Одна из распространённых алгебраических задач – поиск корней уравнения f (x)=0. Для численного отыскания корней проще всего построить график функции y=f (x) и найти точки его пересечения с осью абсцисс (в MATLAB это можно сделать с помощью команд plot, fplot, ezplot). Аналогично можно поступить и в случае системы двух уравнений с двумя неизвестными f (x, у)=0, g (x, y)=0, построив на плоскости (х, у) графики этих функций и найдя точки их пересечения друг с другом. Сложнее обстоит дело с поиском комплексных корней, здесь требуется привлечение специальных методов.
Для поиска корней сложных уравнений с одной переменной, например, включающих логарифмические, тригонометрические, экспоненциальные зависимости, применяют команду fzero. Её входными аргументами служат имя функции, вычисляющей левую часть уравнения f(x)=0, и начальное приближение x0.
Пример 3.1.7. Возьмём полином f(x)=x2+3x+2 с корнями -1 и -2.
В MATLAB их можно найти посредством команды fzero двумя путями. В первом случае нужно сформировать вспомогательную функцию Fun317 в виде отдельного файла во-втором же создать временную функцию (на период данного сеанса MATLAB) при помощи команды inline. Команда fzero, использующая численные методы, возвращает один из корней полинома в зависимости от начального приближения.
Первый способ
1) Создаём m-файл вычисления заданного полинома
function [y] = Fun317(x)
y=x^2+3*x+2;
end
2) Строим график полинома
>>x=-3:0.2:0;
>> y=Fun317(x);
>>plot(x,y,'-k'), grid
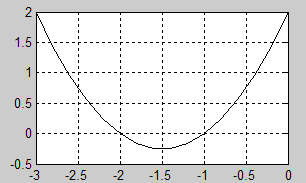 3) Дважды вызываем команду fzero, указывая координаты точек начала интервала поиска
>> x1=fzero(@Fun317,-3)
x1 = -2.000000000000000e+00
>> x2=fzero(@Fun317,0)
x2 = -1
3) Дважды вызываем команду fzero, указывая координаты точек начала интервала поиска
>> x1=fzero(@Fun317,-3)
x1 = -2.000000000000000e+00
>> x2=fzero(@Fun317,0)
x2 = -1
| Второй способ
1) Создаём временную функцию (на период данного сеанса MATLAB) при помощи команды inline.
f(x)=inline(‘x^2+3*x+2’);
2) Строим график полинома
>>x=-3:0.2:0;
>> y=Fun317(x);
>>plot(x,y,'-k'), grid
 3) Дважды вызываем команду fzero, указывая координаты точек начала интервала поиска
>> x1=fzero(f(x),-3)
x1 = -2.000000000000000e+00
>> x2=fzero(f(x),0)
x2 = -1
3) Дважды вызываем команду fzero, указывая координаты точек начала интервала поиска
>> x1=fzero(f(x),-3)
x1 = -2.000000000000000e+00
>> x2=fzero(f(x),0)
x2 = -1
|
В команде fzero и других командах, рассматриваемых ниже, имеется возможность задавать структуру опций решателя. Её можно описать вручную, но удобнее использовать команды optimget и optimset. Для получения полного списка опций и значений по умолчанию применяют формат optimset(‘имя решателя'), например, opts=optimset('fzero'). Для изменения опций используется команда
opts=optimset(‘имя параметра’,значение_параметра).
>> o=optimset('fzero'); %опции команды zero по умолчанию
>> optimget(o,'TolX'); %точность вычислений по умолчанию
>> x1=fzero(@Fun317,-3,o) %оптимизация с точностью 1е-16
x1 = -2.000000000000000e+00
x2=fzero(@Fun317,0,o)
x2 = -1
Уменьшим точность вычислений в предыдущем примере, изменяя опции решателя:
>> o=optimset('fzero'); %опции команды zero по умолчанию
>> о=optimset(o,'TolX',1e-1); %точность вычислений 0.01
>> x1=fzero(@Fun317,-3,o) %оптимизация с точностью 1е-1
x1 = -1.970825976146193e+00
>> x2=fzero(@Fun317,0,o)
x2 = -1.024000000000001e+00
Получили менее точный результат
Для численного решения систем нелинейных алгебраических уравнений с несколькими неизвестными вида F(X)=0, где F – вектор-функция, Х – вектор переменных, предназначена команда fsolve. Ее входными аргументами служат имя функции, оформленной в виде отдельного файла, в которой описаны левые части нелинейных уравнений, и вектор начальных значений переменных. Проиллюстрируем применение этой команды на примере.
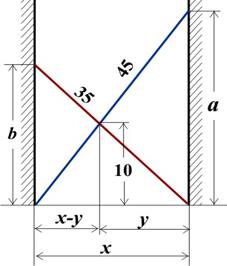
Пример 3.1.8 Задача о двух лестницах.
В узком коридоре крест-накрест стоят две лестницы длиной 45 и 35 метров (рис. 3.4).
Рис.3.5. Графическая иллюстрация и матмодель задачи.
Расстояние от земли до точки их пересечения составляет 10 метров. Определить ширину коридора.
Решение. Обозначим расстояние от верхних точек лестниц до земли через a и b, ширину переулка через x, а расстояние от точки пересечения до левой стенки через y. Тогда можем записать систему 4 уравнений с 4 неизвестными, приведённую на рис. 4.18.
Решим систему в численном виде с помощью команды fsolve. Предварительно составим вспомогательную функцию Fun318, содержащую информацию об уравнениях.
function [fn]=Fun318(p)
x=p(1); y=p(2); a=p(3); b=p(4);
f(1)=x^2 + a^2 - 45^2; f(2)=x^2 + b^2 - 35^2;
f(3)=y/10 - x/b; f(4)=(x-y)/10 - x/a;
fn=f(:);
End
Решаем систему, задав вектор начальных условий [10; 10; 20; 20]
x=fsolve(@Fun318,[10; 10; 20; 20])
Уравнение решено.
fsolve завершил работу, потому что вектор функциональных значений – близок к нулю
как измерено значением по умолчанию функционального допуска, и
проблема кажется регулярной как определено градиентом.
< подробности критериев завершения >
x = 3.181745909535552e+01
2.181893352212048e+01
3.182215103847459e+01
1.458249967308561e+01
Получаем ответ: x =31.8175; y =21.8189; a =31.8222; b =14.5825.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
1. Ознакомиться с теоретическим материалом и ответить на вопросы.
2. Организовать ввод данных и вычисления в интерактивном режиме согласно заданиям.
3. Протоколы выполненных заданий оформить в текстовом процессоре Word, показать преподавателю.
Задание №1
Создайте m-файл, вычисляющий значения функции f(x) на отрезке [ a; b ] с шагом h (Таблица 2.1). Постройте график этой функции с помощью процедуры fplot в границах, заданных в задании. Вычислите интеграл от функции в тех же пределах, используя встроенные функции. Найдите экстремумы и ближайший корень (нуль) функции.
Таблица 2.1
| Вар
| Функция f(x)
| a
| b
| h
| Вар
| Функция f(x)
| a
| b
| h
|
|
| 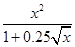
| 1.1
| 3.1
| 0.2
|
| (ex/5)-2(x-1)2
| -1
|
| 0.2
|
|
| 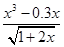
| 2.05
| 3.05
| 0.1
|
| 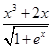
| -0,2
| 0,8
| 0,1
|
|
| 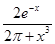
|
| 1.6
| 0.16
|
| 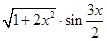
|
|
| 0,2
|
|
| 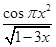
| -1
|
| 0,1
|
| 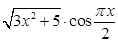
| 0,5
| 1,5
| 0,1
|
|
| 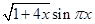
| 0,1
| 0,8
| 0,07
|
| 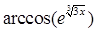
| 0,2
| 0,5
| 0,03
|
|
| 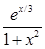
| 1,4
| 2,4
| 0,1
|
| 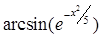
|
|
| 0,5
|
|
| 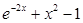
| 0,25
| 2,25
| 0,2
|
| 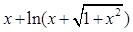
| -0,5
| 0,5
| 0,1
|
|
| 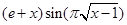
| 1,8
| 2,8
| 0,1
|
| 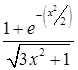
|
|
| 0,2
|
|
| 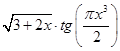
| 0,1
| 0,9
| 0,08
|
| 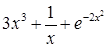
| 1,2
| 2,2
| 0,1
|
|
| 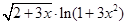
| -0,1
| 0,9
| 0,1
|
| 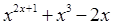
|
|
| 0,4
|
|
| 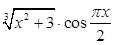
|
| 2,5
| 0,15
|
| 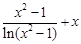
| 2,75
| 4,2
| 0,2
|
|
| 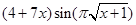
|
|
| 0,7
|
| 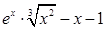
| 2,35
| 4,55
| 0,5
|
|
| 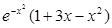
|
|
| 0,2
|
| 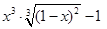
| 8,5
| 12,5
| 0,5
|
|
| 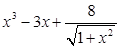
|
| 1,7
| 0,17
|
| 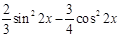
| 6,32
| 7,8
|
|
|
| 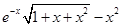
| 6,25
| 6,65
| 0,05
|
| 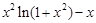
| 7,5
| 9,5
| 0,5
|
Задание №2
Найдите локальные экстремумы функции двух переменных, приняв за начальную, точку с заданными координатами x0, y0 (таблица 2.1). Предварительно создайте соответствующую файл-функцию.
Таблица 2.1
| Вар.
| Функция f(x,y)
| x0
| y0
|
|
| 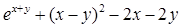
| 0.0
| 1.0
|
|
| 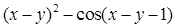
| 0.7
| -1.2
|
|
| 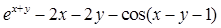
| 1.5
| -0.5
|
|
| 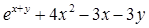
| 0.5
| 1.5
|
|
| 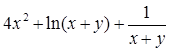
| 0.0
| 1.0
|
|
| 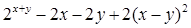
| 1.2
| 0.7
|
|
| 
| 0.0
| -0.9
|
|
| 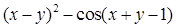
| 0.8
| 1.3
|
|
| 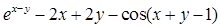
| 1.5
| 0.5
|
|
| 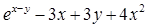
| 0.5
| -1.5
|
|
| 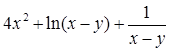
| 0.0
| -1.0
|
|
| 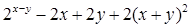
| 1.2
| -0.8
|
Задание №3
Рассчитать аэродинамический нагрев тела в полете со скоростью V, в зависимости от высоты полета H для условий международной стандартной атмосферы (МСА).
Значение высоты H принять от 0 до 25000м с шагом 1000м.
Зависимость температуры атмосферы TH [K]от высоты Н [м] определяется по формуле:
TH = T0 - β·Н
где β - коэффициент снижения температуры β = 6,5·10-3 [K/м];
T0 – температура атмосферы на высоте Н = 0, T0= 288,2[K]
Начиная с высоты 11000м (тропосфера) до высоты 25000м (стратосфера) температура окружающей среды остается постоянной.
Аэродинамический нагрев Δ T* [K] рассчитывается по формуле:
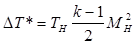
где М Н – число Маха 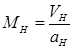 ; аН – местная скорость звука [м/с], определяется по формуле
; аН – местная скорость звука [м/с], определяется по формуле 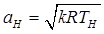 .
.
Показатель адиабаты для воздуха k = 1,4.
Удельная газовая постоянная R = 287,13[Дж/кг·К]
Варианты исходных данных (скорость полета V H)
| Вариант
задания
|
|
|
|
|
|
|
|
|
|
| Скорость
полета
[м/c]
|
|
|
|
|
|
|
|
|
|
В отчете о выполнении задания необходимо:
1. Вывести рассчитанные данные зависимостей TH (Н) и Δ T*(Н) в виде таблиц. Для чего после расчета сохранить их в текстовый файл. Затем ….
2. Построить графики этих зависимостей.



 3) Дважды вызываем команду fzero, указывая координаты точек начала интервала поиска
>> x1=fzero(@Fun317,-3)
x1 = -2.000000000000000e+00
>> x2=fzero(@Fun317,0)
x2 = -1
3) Дважды вызываем команду fzero, указывая координаты точек начала интервала поиска
>> x1=fzero(@Fun317,-3)
x1 = -2.000000000000000e+00
>> x2=fzero(@Fun317,0)
x2 = -1
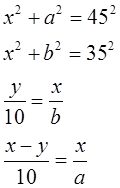
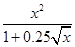
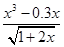
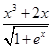
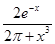
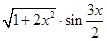
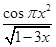
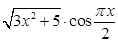
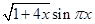
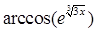
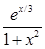
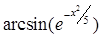
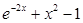
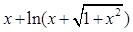
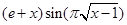
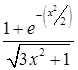
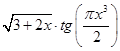
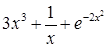
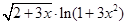
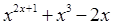
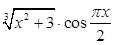
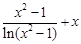
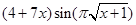
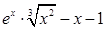
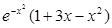
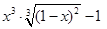
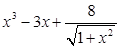
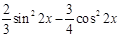
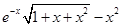
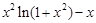
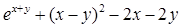
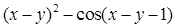
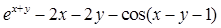
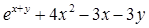
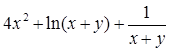
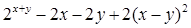

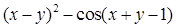
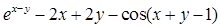
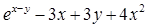
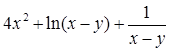
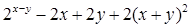
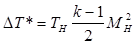
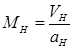 ; аН – местная скорость звука [м/с], определяется по формуле
; аН – местная скорость звука [м/с], определяется по формуле 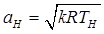 .
.


