ИНЖЕНЕРНО-ВЫЧИСЛИТЕЛЬНЫЕ ТЕХНОЛОГИИ
Лабораторная работа № 3.
Решение типовых задач алгебры и анализа
Создание процедур (файлов-функций) в среде MatLAB
Цель работы:
Создание простейших подпрограмм (файл-функций)
3.2.1. Общие требования к структуре файл-функций.
Файл-функция (процедура-функция) должна начинаться со строки заголовка
function [< ПКВ >] = < имя процедуры >(< ПВВ >).
Если перечень конечных (выходных) величин (ПКВ) содержит только один объект (в общем случае - матрицу), то файл-функция представляет собой обычную функцию (одной или нескольких переменных). Фактически даже в этом простейшем случае файл-функция является уже процедурой в обычном смысле других языков программирования, если выходная величина является вектором или матрицей. Первая строка в этом случае имеет вид:
function <имя переменной> = <имя процедуры>(<ПВВ>).
Если же в результате выполнения файл-функции должны быть определены (вычислены) несколько объектов (матриц), такая файл-функция представляет собой уже более сложный объект, который в программировании обычно называется процедурой (в языке Паскаль), или подпрограммой. Общий вид первой строки в этом случае становится таким:
function [ y1, y2,..., yn ] = <имя процедуры>(<ПВВ>),
т. е. перечень выходных величин y1, y2,..., y должен быть представлен как вектор-строка с элементами y1, y2,..., y (все они могут быть матрицами).
В простейшем случае заголовок функции одной переменной приобретёт вид:
function y = func(x)
где func - имя функции (m-файла).
Пример 3.1 Рассмотрим составление m-файла для вычисления функции

Для открытия редактора m-файла следует активизировать меню < File> < New> < M-File > командного окна MatLAB. На экране появится окно текстового редактора. В нем нужно набрать текст:
function [y] = Fun331(x,d)
%Процедура, которая вычисляет значение функции
% y = (d3)*ctg(x)*sqrt(sin(x)4-cos(x)4).
% Обращение y = F1(x,d).
y = (d^3).*cot(x).*sqrt(sin(x).^4-cos(x).^4);
После этого необходимо сохранить этот текст в файле под именем (допустим) F331.m в вашем активном каталоге. Необходимый m-файл создан. Теперь можно пользоваться этой функцией при расчётах. Так, если ввести команду в окне Command Window
» y = Fun331(1, 0.1)
то получим результат
y =
4. 1421e-04.
Следует заметить, что аналогично можно получить сразу вектор всех значений указанной функции при разных значениях аргумента Так, если сформировать вектор zet
» zet= 0:0.3:1.8;
и обратиться в ту же процедуру
» my = F331(zet,1)
то получим:
my =
Columns 1 through 6
0 + Infi 0 + 2.9369i 0 + 0.8799i 0.3783 0.3339 0.0706
Column 7
-0.2209
Примечания.
1. Возможность использования сформированной процедуры как для отдельных чисел, так и для векторов и матриц обусловлена применением в записи соответствующего M-файла вместо обычных знаков арифметических действий их аналогов с предшествующей точкой (.*./.^)
2. Во избежание вывода на экран нежелательных промежуточных результатов, необходимо в тексте процедуры все вычислительные операторы завершать символом "; ".
3. Как показывают приведённые примеры, имена переменных, указанные в заголовке файл-функции могут быть любыми, т. е. носят формальный характер. Важно, чтобы структура обращения полностью соответствовала структуре заголовка в записи текста M-файла и чтобы переменные в этом обращении имели тот же тип и размер, как и в заголовке M-файла.
Чтобы получить информацию о созданной процедуре, достаточно набрать в командном окне команду:
» help F331,
и в командном окне появится
Процедура, которая вычисляет значение функции
y = (d3)*ctg(x)*sqrt(sin(x)4-cos(x)4).
Обращение y = F1(x,d)
Пример 3.2 Другой пример. Построим график двух функций:
y1 = 200 sin(x)/x; y2 = x2.
Для этого создадим m-файл, который вычисляет значения этих функций:
function [y] = Fun332(x)
%Вычисление двух функций
% y(1) = 200 sin(x)/x и y(2) = x2.
y(:,1) = 200*sin(x)./x;
y(:,2) = x*2;
End
Теперь построим графики этих функций в окне Command Window
>> fplot('Fun332', [-20 20], 50, 2), grid
>> set(gcf,'color','white'); title('График функций "y(1) = 200 sin(x)/x и y(2) = x2"')
Результат изображён на рис. 2.1.

Рис. 3.1.График функций y1 = 200 sin(x)/x; y2 = x2.
Пример 3.3 Cоздание файл-функции, вычисляющей значения функции
y(t) = k1+k2·t+k3·sin(k4·t+k5)
В этом случае удобно объединить совокупность коэффициентов k в единый вектор К:
К = [k1 k2 k3 k4 k5] и создать такой M-файл:
function [y] = Fun333(x,K)
%Вычисление функции
% y = K(1)+K(2)*x+K(3)*sin(K(4)*x+K(5)),
% где К - вектор из пяти элементов
% Используется для определения текущих значений
% параметров движения объекта
y = K(1)+K(2)*x+K(3)*sin(K(4)*x+K(5));
End
Тогда расчёт, например, 11-ти значений этой функции можно осуществить так
» K = ones(1,5);
» t = 0:1:10;
» fi = Fun333(t, K)
fi =
1. 8415 2. 9093 3. 1411 3. 2432 4. 0411 5. 7206 7. 6570 8. 9894 9. 4560 10. 0000
3.2.2. Типовое оформление файла-функции
Рекомендуется оформлять m-файл процедуры-функции по такой схеме:
function [<Выходные парам.>] = <имя функции>(<Входные парам.>)
% <Краткое пояснение назначения процедуры>
% Входные переменные
%<Детальное пояснение о назначении, типе и размерах
% каждой из переменных, перечисленных в перечне <Входные парам.>
% Выходные переменные
% <Детальное пояснение о назначении, типе и размерах
% каждой из переменных перечня <Выходные парам.>
% и величин, используемых в процедуре как глобальные>
% Использование других функций и процедур
% <Раздел заполняется, если процедура содержит обращение
% к другим процедурам, кроме встроенных процедур MatLab>
< П у с т а я с т р о к а >
% Автор: < Указывается автор процедуры, дата создания конечного варианта
% процедуры и организация, в которой созданная программа>
< Т е к с т и с п о л н я е м о й ч а с т и п р о ц е д у р ы >
Перечень входных и выходных переменных, разделяется запятыми.
Примечание. При использовании команды help <имя процедуры> в командное окно выводятся строки комментария до первой пустой строки.
3.2.3 Функции функций
Некоторые важные универсальные процедуры в MatLAB используют в качестве переменного параметра имя функции, с которой они оперируют, и поэтому требуют при обращении к ним указания имени M-файла, в котором записан текст некоторой другой процедуры (функции). Такие процедуры называют функциями функций.
Чтобы воспользоваться такой функцией от функции, необходимо, чтобы пользователь предварительно создал M-файл, в котором вычислялось бы значение нужной функции по известному значению её аргумента.
Перечислим некоторые из стандартных функций от функций, предусмотренных в MatLAB.
Вычисление определённых интегралов
Для вычисления интегралов методом трапеций в системе MATLAB предусмотрена функция trapz:
Integ = trapz (х,у);
Одномерный массив х (вектор) содержит дискретные значения аргументов подынтегральной функции. Значения подынтегральной функции в этих точках сосредоточены в одномерном массиве у. Чаще всего для интегрирования выбирают равномерную сетку, то есть значения элементов массива х отстоят друг от друга на одну и ту же величину (шаг интегрирования). Точность вычисления интеграла зависит от величины шага интегрирования: чем меньше этот шаг, тем больше точность.
Вычислим простой интеграл методом трапеций с шагом интегрирования π/10.

>> x = 0:pi/10:pi;
>> y=cos(x);
>> J1 = trapz(x,y)
J1 =
1.387778780781446e-16
Обычно для достижения высокой точности требуется выполнять интегрирование с очень малыми шагами, а контроль достигнутой точности осуществлять путём сравнения последовательных результатов. При одном и том же шаге интегрирования методы более высоких порядков точности достигают более точных результатов.
В системе MatLab методы интегрирования более высоких порядков точности реализуются функцией: quad (метод квадратур)
Как и многие другие функции системы MATLAB, функция quad может принимать различное количество параметров. Полный формат вызова этой функции
Q = quad(‘Fun’,a,b,Tol,Trace)
альтернативный вариант вызова
Q = quad(@Fun,a,b,Tol,Trace)
включает в себя три параметра: ‘Fun’ (@Fun) - имя подынтегральной функции; a - нижний предел интегрирования; b - верхний предел интегрирования; Tol – требуемая точность вычислений и Trace – графическое сопровождение процесса вычисления. По умолчанию погрешность вычисления равна 1Е-06.
Из высшей математики известно, что к определённым интегралам могут быть сведены многие другие типы интегралов, например криволинейные интегралы. Таким образом, с помощью функций quad, quad8 (или trapz) можно вычислить и эти интегралы.
Примеры:
Q = quad(@myfun,0,2);
myfun.m файл с подынтегральной функцией:
%-------------------%
function y = myfun(x)
y = 1./(x.^3-2*x-5);
%-------------------%
Если функция имеет в качестве дополнительного параметра константу:
Q = quad(@(x)myfun2(x,5),0,2);
myfun2.m - файл с подынтегральной функцией
%----------------------%
function y = myfun2(x,c)
y = 1./(x.^3-2*x-c);
%----------------------%
Пример 3.1.1 Рассмотрим пример вычисления криволинейного интеграла первого рода. Пусть требуется вычислить массу М винтовой линии С:
х = sin(t); у = 2cos(t); z =3t; 0 <= t <= 2
с постоянной линейной плотностью, равной 5.
Задача решается с помощью криволинейного интеграла первого рода:

который сводится к вычислению следующего обыкновенного определённого интеграла:


Для вычисления подынтегральной функции создадим следующий текст:
function [z] = Fun311(t)
%Вычисляет значение функции
% z = sqrt(cos(t)^2 + 4*sin(t)^2 +9)
z = sqrt(cos(t).^2 + 4*sin(t).^2+9);
End
который запишем в файл Fun311.m, после чего вызываем функцию quad:
M = 5*quad('Fun311',0,2)
М =
34.2901
Двойные интегралы в системе MATLAB вычисляются с помощью специальной функции dblquad.
Пример 3.1.2 Вычислим интеграл:

Оформим подынтегральную функцию в следующем виде:
function z = Fun312(x, у)
z = x.*sin(y) + y.*sin(x);
(записав этот текст в файл Fun312.m) и вызовем функцию dblquad:
J = dblquad('Fun312', 0, 1, 1, 2);
J =
1.1678
Пример 3.1.3 Вычислить значение интеграла функции y(x) на отрезке [1;3] с шагом 0.1 и построить график на отрезке интегрирования при d= 5.

Последовательность действий будет такой:
1) Создаем процедуру (подпрограмму) F1 вычисления y(x) и сохраняем в файле F1.m
function [y] = Fun313(x,d)
%Процедура вычисляет значение функции
% y = d^3*sqrt(sin(x)4+cos(x)4).
% Обращение y = F1(x,d).
y = d^3*sqrt(sin(x).^4+cos(x).^4);
End
где y – выходной параметр (возвращает результат работы процедуры)
x,d - входные параметры (передаёт в процедуру значение аргумента x и константы d)
2) Вычисляем значение интеграла используя процедуру quad не задавая шаг интегрирования.
>> d=5;
>> M =d^3*quad(@(x)Fun313(x,d), 1, 3)
M =
2.701850399088707e+04
2) Строим график заданной функции
>> z= 1:0.1:3;
>> my = Fun313(z,5);
>> plot(z,my)
>> xlabel('(x)'); ylabel('(y)');
>> set(gcf,'color','white'); title('График функции "y = (d3)*sqrt(sin(x)4+cos(x)4)."')
В результате получим график (Рис.3.1)

Рис. 3.2График функции 
Пример 3.1.4
Определить экстремумы функции y=x4-0.5x3-28x2+140 на отрезке [-4;6]
В M-файле с именем Fun314.m пишем:
function [y] = Fun314(x)
y=x.^4-0.5*x.^3-28*x.^2+140;
End
Потом в командном окне пишем:
x=-4:0.1:6;
y=x.^4-0.5*x.^3-28*x.^2+140;
Plot(x,y,'-k'), grid
Опираясь на полученный график (Рис.3.3 а) функции задаём интервалы поиска локальных экстремумов.
% Ближайший минимум функции от точки x=-4
y=Fun314(x);
[xmin,ymin]=fminsearch(@Fun314,-4)
xmin = -3.558886718750000e+00
ymin = -3.168172523631594e+01
Для другого интервала [0;5]
% Минимум функции на интервале от точки x=3
[xmin,ymin]=fminsearch(@Fun314,3)
xmin = 3.933875000000005e+00
ymin = -8.426236646759048e+01
Для определения максимума ставим знак минус перед вычислением f(x) в функции записанной в файле Fun341 и сохраняем его с именем Fun341a
function [y] = Fun314a(x)
y=-(x.^4-0.5*x.^3-28*x.^2+140);
End
строим график записанной нами функции Fun341a (Рис.3.2.б)
>> x=-4:0.1:6;
>> y=Fun314a(x);
>> plot(x,y,'-k'), grid
И определяем «минимум» в интервале [-2,2], который является максимумом для исходной функции
[xmax,ymax]=fminsearch(@Fun314a,-2,2)
xmax = 1.776356839400251e-15
ymax = -140
 а)
а)
|  б)
б)
|
Рис.3.3 Определение экстремумов функции y=x4-0.5x3-28x2+140 на отрезке [-4;6]
End
>> [z,fval]=fminunc(@Fun316,[3 3],optimset('Gradobj','on'))
Локальный минимум найден.
Процесс оптимизации завершён, потому что шаг градиента - меньше чем
значение по умолчанию функционального допуска.
< подробности критериев остановки >
z = 0 0
fval = 0
Из полученного результата можно сделать вывод, что функция fminunc выполняет задачу с большей точностью, чем функция fminsearch. Но для её использования необходимо хорошо представлять математический аппарат алгоритма нахождения экстремума функции.
Рис.3.5. Графическая иллюстрация и матмодель задачи.
Расстояние от земли до точки их пересечения составляет 10 метров. Определить ширину коридора.
Решение. Обозначим расстояние от верхних точек лестниц до земли через a и b, ширину переулка через x, а расстояние от точки пересечения до левой стенки через y. Тогда можем записать систему 4 уравнений с 4 неизвестными, приведённую на рис. 4.18.
Решим систему в численном виде с помощью команды fsolve. Предварительно составим вспомогательную функцию Fun318, содержащую информацию об уравнениях.
function [fn]=Fun318(p)
x=p(1); y=p(2); a=p(3); b=p(4);
f(1)=x^2 + a^2 - 45^2; f(2)=x^2 + b^2 - 35^2;
f(3)=y/10 - x/b; f(4)=(x-y)/10 - x/a;
fn=f(:);
End
Решаем систему, задав вектор начальных условий [10; 10; 20; 20]
x=fsolve(@Fun318,[10; 10; 20; 20])
Уравнение решено.
fsolve завершил работу, потому что вектор функциональных значений – близок к нулю
как измерено значением по умолчанию функционального допуска, и
проблема кажется регулярной как определено градиентом.
< подробности критериев завершения >
x = 3.181745909535552e+01
2.181893352212048e+01
3.182215103847459e+01
1.458249967308561e+01
Получаем ответ: x =31.8175; y =21.8189; a =31.8222; b =14.5825.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
1. Ознакомиться с теоретическим материалом и ответить на вопросы.
2. Организовать ввод данных и вычисления в интерактивном режиме согласно заданиям.
3. Протоколы выполненных заданий оформить в текстовом процессоре Word, показать преподавателю.
Задание №1
Создайте m-файл, вычисляющий значения функции f(x) на отрезке [ a; b ] с шагом h (Таблица 2.1). Постройте график этой функции с помощью процедуры fplot в границах, заданных в задании. Вычислите интеграл от функции в тех же пределах, используя встроенные функции. Найдите экстремумы и ближайший корень (нуль) функции.
Таблица 2.1
| Вар
| Функция f(x)
| a
| b
| h
| Вар
| Функция f(x)
| a
| b
| h
|
|
| 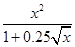
| 1.1
| 3.1
| 0.2
|
| (ex/5)-2(x-1)2
| -1
|
| 0.2
|
|
| 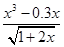
| 2.05
| 3.05
| 0.1
|
| 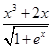
| -0,2
| 0,8
| 0,1
|
|
| 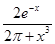
|
| 1.6
| 0.16
|
| 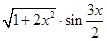
|
|
| 0,2
|
|
| 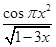
| -1
|
| 0,1
|
| 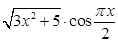
| 0,5
| 1,5
| 0,1
|
|
| 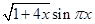
| 0,1
| 0,8
| 0,07
|
| 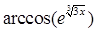
| 0,2
| 0,5
| 0,03
|
|
| 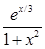
| 1,4
| 2,4
| 0,1
|
| 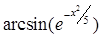
|
|
| 0,5
|
|
| 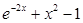
| 0,25
| 2,25
| 0,2
|
| 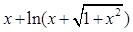
| -0,5
| 0,5
| 0,1
|
|
| 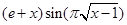
| 1,8
| 2,8
| 0,1
|
| 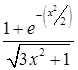
|
|
| 0,2
|
|
| 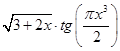
| 0,1
| 0,9
| 0,08
|
| 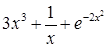
| 1,2
| 2,2
| 0,1
|
|
| 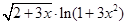
| -0,1
| 0,9
| 0,1
|
| 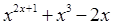
|
|
| 0,4
|
|
| 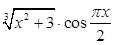
|
| 2,5
| 0,15
|
| 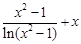
| 2,75
| 4,2
| 0,2
|
|
| 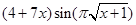
|
|
| 0,7
|
| 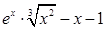
| 2,35
| 4,55
| 0,5
|
|
| 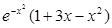
|
|
| 0,2
|
| 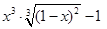
| 8,5
| 12,5
| 0,5
|
|
| 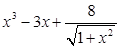
|
| 1,7
| 0,17
|
| 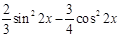
| 6,32
| 7,8
|
|
|
| 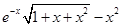
| 6,25
| 6,65
| 0,05
|
| 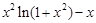
| 7,5
| 9,5
| 0,5
|
Задание №2
Найдите локальные экстремумы функции двух переменных, приняв за начальную, точку с заданными координатами x0, y0 (таблица 2.1). Предварительно создайте соответствующую файл-функцию.
Таблица 2.1
| Вар.
| Функция f(x,y)
| x0
| y0
|
|
| 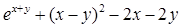
| 0.0
| 1.0
|
|
| 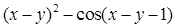
| 0.7
| -1.2
|
|
| 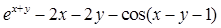
| 1.5
| -0.5
|
|
| 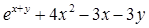
| 0.5
| 1.5
|
|
| 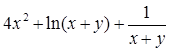
| 0.0
| 1.0
|
|
| 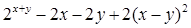
| 1.2
| 0.7
|
|
| 
| 0.0
| -0.9
|
|
| 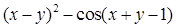
| 0.8
| 1.3
|
|
| 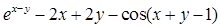
| 1.5
| 0.5
|
|
| 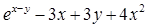
| 0.5
| -1.5
|
|
| 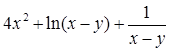
| 0.0
| -1.0
|
|
| 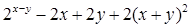
| 1.2
| -0.8
|
Задание №3
Рассчитать аэродинамический нагрев тела в полете со скоростью V, в зависимости от высоты полета H для условий международной стандартной атмосферы (МСА).
Значение высоты H принять от 0 до 25000м с шагом 1000м.
Зависимость температуры атмосферы TH [K]от высоты Н [м] определяется по формуле:
TH = T0 - β·Н
где β - коэффициент снижения температуры β = 6,5·10-3 [K/м];
T0 – температура атмосферы на высоте Н = 0, T0= 288,2[K]
Начиная с высоты 11000м (тропосфера) до высоты 25000м (стратосфера) температура окружающей среды остается постоянной.
Аэродинамический нагрев Δ T* [K] рассчитывается по формуле:
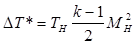
где М Н – число Маха 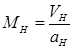 ; аН – местная скорость звука [м/с], определяется по формуле
; аН – местная скорость звука [м/с], определяется по формуле 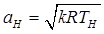 .
.
Показатель адиабаты для воздуха k = 1,4.
Удельная газовая постоянная R = 287,13[Дж/кг·К]
Варианты исходных данных (скорость полета V H)
| Вариант
задания
|
|
|
|
|
|
|
|
|
|
| Скорость
полета
[м/c]
|
|
|
|
|
|
|
|
|
|
В отчете о выполнении задания необходимо:
1. Вывести рассчитанные данные зависимостей TH (Н) и Δ T*(Н) в виде таблиц. Для чего после расчета сохранить их в текстовый файл. Затем ….
2. Построить графики этих зависимостей.
ИНЖЕНЕРНО-ВЫЧИСЛИТЕЛЬНЫЕ ТЕХНОЛОГИИ
Лабораторная работа № 3.
Решение типовых задач алгебры и анализа
Создание процедур (файлов-функций) в среде MatLAB
Цель работы:












 а)
а)
 б)
б)
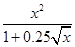
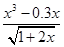
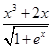
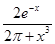
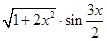
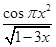
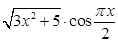
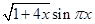
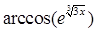
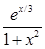
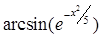
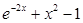
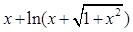
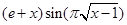
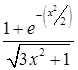
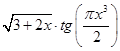
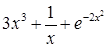
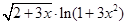
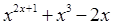
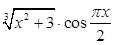
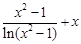
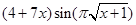
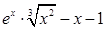
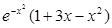
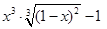
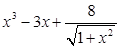
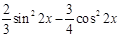
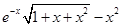
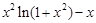
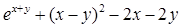
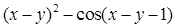
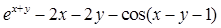
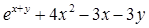
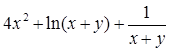
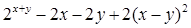

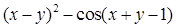
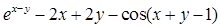
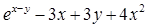
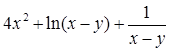
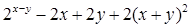
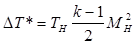
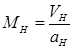 ; аН – местная скорость звука [м/с], определяется по формуле
; аН – местная скорость звука [м/с], определяется по формуле 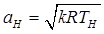 .
.


