О п р е д е л е н и е 11. Числовой ряд вида
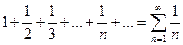 (10)
(10)
называется гармоническим рядом.
О п р е д е л е н и е 12. Числовой ряд вида
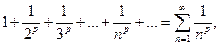 где
где 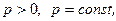 (11)
(11)
называется рядом Дирихле (или обобщенным гармоническим рядом).
З а м е ч а н и е 7. Ряд (10) можно рассматривать как частный случай ряда (11) при 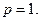
Т е о р е м а 5. Ряд Дирихле (11) сходится при 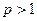 и расходится при
и расходится при 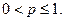
З а м е ч а н и е 4. Ряд (11), где 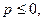 также является расходящимся. Но в этом случае для него не выполнено необходимое условие сходимости, так как
также является расходящимся. Но в этом случае для него не выполнено необходимое условие сходимости, так как
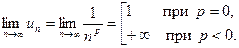
Поэтому числовой ряд (11) сходится при 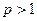 и расходится при
и расходится при 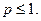
ПРИЗНАКИ СРАВНЕНИЯ ПОЛОЖИТЕЛЬНЫХ РЯДОВ
Т е о р е м а 6 (первый признак сравнения). Пусть члены положительных рядов
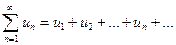 (12)
(12)
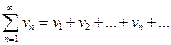 (13)
(13)
удовлетворяют неравенству:
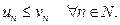 (14)
(14)
Тогда: если ряд (13) сходится, то сходится ряд (12); если ряд (12) расходится, то расходится ряд (13).
З а м е ч а н и е 9. Теорема 6 сохраняет силу, если условие (14) будет выполнено, начиная с некоторого номера  (так как отбрасывание или приписывание к ряду любого конечного числа первых членов не меняет характер сходимости ряда).
(так как отбрасывание или приписывание к ряду любого конечного числа первых членов не меняет характер сходимости ряда).
Т е о р е м а 7 (второй признак сравнения). Пусть члены положительных рядов (12) и (13) таковы, что существует конечный предел
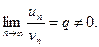 (15)
(15)
Тогда ряды (12) и (13) эквивалентны с точки зрения сходимости, то есть сходятся или расходятся одновременно.
З а м е ч а н и е 10. Для сравнения с данным рядом во многих случаях целесообразно в качестве второго ряда выбирать ряд Дирихле 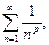 который сходится, если
который сходится, если 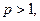 и расходится, если
и расходится, если 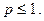
ПРИЗНАК ДАЛАМБЕРА
Т е о р е м а 8 (признак Даламбера). Пусть для положительного ряда (7) существует конечный предел
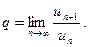 (16)
(16)
Тогда при 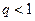 ряд (7) сходится, при
ряд (7) сходится, при 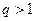 ряд (7) расходится. При
ряд (7) расходится. При 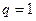 вопрос о сходимости или расходимости ряда (7) остается нерешенным.
вопрос о сходимости или расходимости ряда (7) остается нерешенным.
З а м е ч а н и е 11. Если
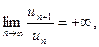
То, как и в случае 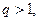 ряд (7) расходится.
ряд (7) расходится.
РАДИКАЛЬНЫЙ ПРИЗНАК КОШИ
Т е о р е м а 9 (радикальный признак Коши). Пусть для положительного ряда (7) существует конечный предел
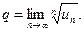 (17)
(17)
Тогда при 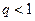 ряд (7) сходится; при
ряд (7) сходится; при 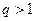 ряд (7) расходится; при
ряд (7) расходится; при 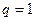 вопрос о сходимости ряда (7) остается нерешенным.
вопрос о сходимости ряда (7) остается нерешенным.
З а м е ч а н и е 12. Если 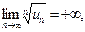 то, как и при
то, как и при 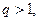 ряд (7) расходится.
ряд (7) расходится.
ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Указать седьмой член последовательности
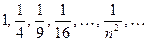 .
.
Р е ш е н и е. Нетрудно видеть, что общий член рассматриваемой последовательности задается формулой: 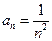 . Придавая числу
. Придавая числу 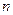 разные значения из множества натуральных чисел, находим члены последовательности. Например,
разные значения из множества натуральных чисел, находим члены последовательности. Например,
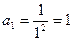 ,
, 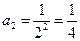 ,
, 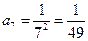 .
.
О т в е т: 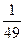 .
.
Пример 2. Найти общий член последовательности
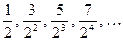 . (18)
. (18)
Указать ее 18-й член.
Решение. Заметим, что числители дробей (7)образуют арифметическую прогрессию 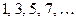 , у которой первый член
, у которой первый член 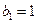 и разность
и разность 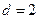 .
.
Поэтому 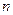 -й член последовательности нечетных натуральных чисел находим по формуле:
-й член последовательности нечетных натуральных чисел находим по формуле:
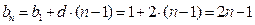 .
.
Знаменатели дробей (18) образуют геометрическую прогрессию 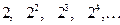 , у которой
, у которой 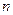 -й член вычисляется по формуле
-й член вычисляется по формуле 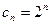 . Следовательно, общий член последовательности (18) задается формулой:
. Следовательно, общий член последовательности (18) задается формулой: 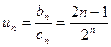 . Поэтому заключаем:
. Поэтому заключаем: 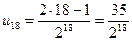 .
.
Ответ: 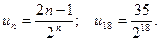
П р и м е р 3. Найти общий член ряда:
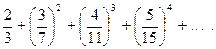
Р е ш е н и е. Показатель степени каждого члена совпадает с номером этого члена, поэтому показатель 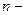 го члена равен
го члена равен 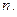 Числители дробей
Числители дробей 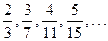 образуют арифметическую прогрессию, где
образуют арифметическую прогрессию, где 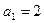 и
и 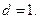 Поэтому
Поэтому 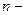 й числитель равен
й числитель равен 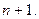 Знаменатели указанных дробей образуют арифметическую прогрессию с
Знаменатели указанных дробей образуют арифметическую прогрессию с 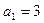 и
и 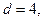 поэтому
поэтому 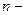 й знаменатель равен
й знаменатель равен 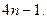 Тогда общим членом ряда является
Тогда общим членом ряда является 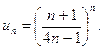
О т в е т: 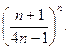
Пример 4. Исследовать на сходимость ряд:
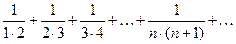 . (19)
. (19)
Р е ш е н и е. Для ряда (19) имеем:
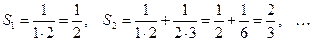 ,
,
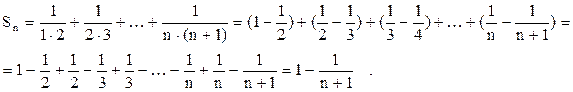
Следовательно, 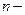 я частичная сумма ряда (8) вычисляется по формуле:
я частичная сумма ряда (8) вычисляется по формуле:
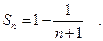
Поэтому 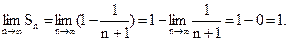 Значит, ряд (19) сходится и его сумма
Значит, ряд (19) сходится и его сумма 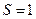 .
.
О т в е т: сходится, 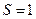 .
.
Пример 5. Исследовать сходимость ряда
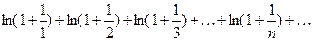 . (20)
. (20)
Р е ш е н и е. Найдем для него 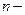 ю частичную сумму:
ю частичную сумму:
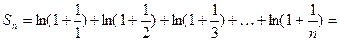
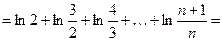
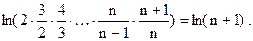
Следовательно, 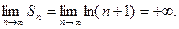 Поэтому ряд (20) расходится.
Поэтому ряд (20) расходится.
О т в е т: расходится.
Пример 6. Исследовать на сходимость положительный ряд
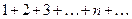 .. (21)
.. (21)
Решение. В данном случае общий член ряда задается формулой 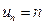 , откуда находим:
, откуда находим:
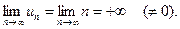
Следовательно, нарушено необходимое условие сходимости ряда и по замечанию 2 ряд (21) расходится.
Ответ: ряд расходится.
Пример 7. Исследовать сходимость рядов: 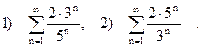
Решение.  В этом случае ряд составлен из членов геометрической прогрессии, где
В этом случае ряд составлен из членов геометрической прогрессии, где 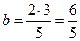 и
и 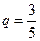 . Так как
. Так как 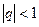 , то по теореме 2 ряд сходится и его сумма вычисляется по формуле:
, то по теореме 2 ряд сходится и его сумма вычисляется по формуле: 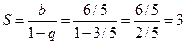 .
.
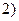 В этом случае ряд составлен из членов геометрической прогрессии, где
В этом случае ряд составлен из членов геометрической прогрессии, где 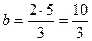 и
и 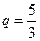 . Так как
. Так как 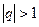 , то по теореме 2 ряд расходится.
, то по теореме 2 ряд расходится.
Ответ: 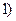 сходится,
сходится, 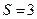 ;
; 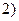 расходится.
расходится.
Пример 8. Исследовать сходимость ряда
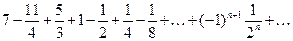 . (22)
. (22)
Решение. Рассмотрим вспомогательный числовой ряд
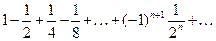 , (23)
, (23)
полученный из ряда (22) отбрасыванием первых трех членов. Видим, что ряд (23) составлен из членов геометрической прогрессии 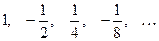 с первым членом
с первым членом 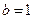 и знаменателем
и знаменателем 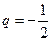 , значит,
, значит, 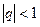 . Следовательно, по теореме 2 ряд (23) сходится и имеет сумму
. Следовательно, по теореме 2 ряд (23) сходится и имеет сумму
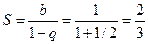 .
.
Поэтому, воспользовавшись свойством 2, получаем: ряд (11) сходится и его сумма равна числу:
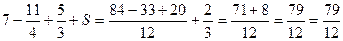 .
.
Ответ: сходится, 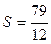 .
.
П р и м е р 9. Найти сумму ряда 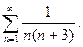
Р е ш е н и е. Заметим, что для любого натурального числа 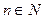 справедливо равенство:
справедливо равенство:
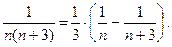
Применим эту формулу для вычисления частичной суммы 
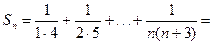
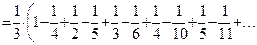
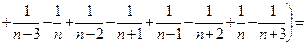
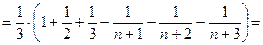
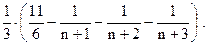
Следовательно, 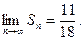
О т в е т: 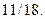
П р и м е р 10. Исследовать сходимость ряда: 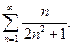
Р е ш е н и е. Рассмотрим функцию 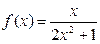 при
при 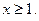 Она непрерывна на
Она непрерывна на 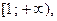 положительна и монотонно убывает (
положительна и монотонно убывает (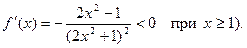 Поэтому интегральный признак Коши применим к рассматриваемому ряду.
Поэтому интегральный признак Коши применим к рассматриваемому ряду.
Вычислим интеграл:
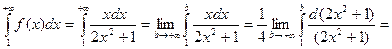
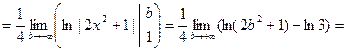
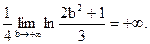
Итак, по интегральному признаку Коши из расходимости интеграла следует расходимость изучаемого в примере ряда.
О т в е т: расходится.
П р и м е р 11. Исследовать сходимость ряда: 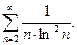
Р е ш е н и е. Рассмотрим функцию 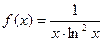 ,
, 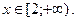 Она непрерывна при
Она непрерывна при 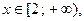 положительна, монотонно убывает (так как
положительна, монотонно убывает (так как 
Вычислим интеграл:
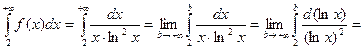
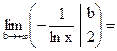
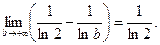
Следовательно, несобственный интеграл 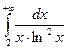 сходится. Значит, по интегральному признаку Коши сходится рассматриваемый в примере ряд.
сходится. Значит, по интегральному признаку Коши сходится рассматриваемый в примере ряд.
О т в е т: сходится.
П р и м е р 12. Исследовать на сходимость ряды:
а) 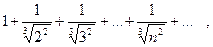 б)
б) 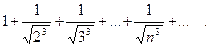
Р е ш е н и е. Ряд а) совпадает со следующим:  . Он расходится как ряд Дирихле с показателем
. Он расходится как ряд Дирихле с показателем 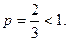 Ряд б) совпадает со следующим:
Ряд б) совпадает со следующим: 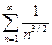 . Он сходится как ряд Дирихле с показателем
. Он сходится как ряд Дирихле с показателем 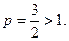
О т в е т: а) расходится; б) сходится.
П р и м е р 13. Исследовать сходимость ряда: 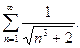
Р е ш е н и е. Общий член данного ряда задается формулой: 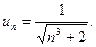
Рассмотрим вспомогательный ряд 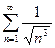 с общим членом
с общим членом 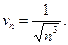 Нетрудно видеть, что
Нетрудно видеть, что 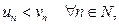 так как
так как
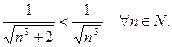
Значит, вспомогательный ряд сходится как ряд Дирихле с показателем 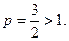 Следовательно, по первому признаку сравнения положительных рядов следует сходимость исходного ряда.
Следовательно, по первому признаку сравнения положительных рядов следует сходимость исходного ряда.
О т в е т: сходится.
П р и м е р 14. Исследовать на сходимость ряд: 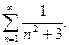
Р е ш е н и е. В данном случае 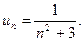 Рассмотрим вспомогательный ряд
Рассмотрим вспомогательный ряд 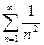 , для которого
, для которого 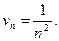 Так как
Так как 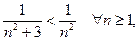 то есть
то есть 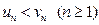 . Следовательно, выполнены условия первого признака сравнения рядов.
. Следовательно, выполнены условия первого признака сравнения рядов.
Известно, что выбранный вспомогательный ряд - ряд Дирихле с показателем 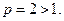 Следовательно, он сходится. Тогда по первому признаку сравнения будет сходиться и данный в примере ряд.
Следовательно, он сходится. Тогда по первому признаку сравнения будет сходиться и данный в примере ряд.
О т в е т: сходится.
П р и м е р 15. Исследовать на сходимость ряд:
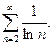 (24)
(24)
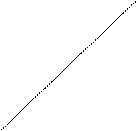
Р е ш е н и е. Для сравнения с рядом (24) возьмем расходящийся гармонический ряд 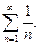 На рис. 1 даны графики функций
На рис. 1 даны графики функций 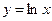 и
и 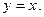 Очевидно, что
Очевидно, что 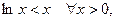 в частности, при
в частности, при 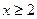 , где
, где 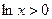 . Тогда
. Тогда 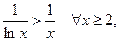 откуда заключаем:
откуда заключаем: 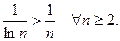
 у
у
у = х
 у = lnx
у = lnx

 1
1
 О 1 е х
О 1 е х
Рис. 1
Следовательно, по первому признаку сравнения из расходимости гармонического ряда следует расходимость исходного ряда (24).
О т в е т: расходится.
П р и м е р 16. Исследовать сходимость ряда: 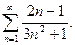
Р е ш е н и е. Применим второй признак сравнения, рассмотрев дополнительно гармонический ряд. Тогда 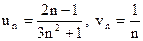 , откуда получаем
, откуда получаем
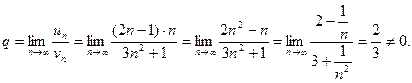
Следовательно, учитывая, что гармонический ряд расходится, расходящимся является рассматриваемый в примере ряд.
О т в е т: расходится.
П р и м е р 17. Исследовать сходимость ряда:
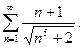 (25)
(25)
Р е ш е н и е. Заметим, что для ряда (25) общий член при больших значениях числа 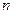 удовлетворяет приближенному равенству:
удовлетворяет приближенному равенству:
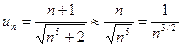 .
.
Поэтому для сравнения с рядом (25) возьмем ряд Дирихле 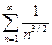 с показателем
с показателем 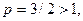 а значит, сходящийся. Его общий член задается формулой:
а значит, сходящийся. Его общий член задается формулой: 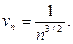
Вычислим предел:
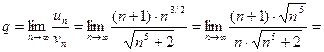

Следовательно, по второму признаку сравнения ряд (26) сходится.
О т в е т: сходится.
П р и м е р 18. Исследовать сходимость ряда: 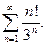
Р е ш е н и е. Напомним, что 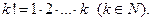 Для данного ряда
Для данного ряда 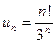 и
и 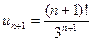 .
.
Вычислим предел:
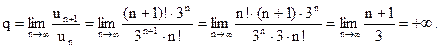
Следовательно, исходный ряд расходится по признаку Даламбера.
О т в е т: расходится.
П р и м е р 19. Исследовать сходимость ряда: 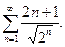
Р е ш е н и е. Для данного ряда 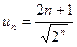 и
и 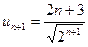 . Поэтому получаем:
. Поэтому получаем:
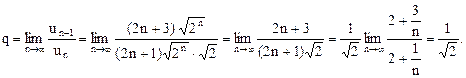
Следовательно, учитывая, что 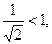 то по признаку Даламбера заключаем: рассматриваемый ряд сходится.
то по признаку Даламбера заключаем: рассматриваемый ряд сходится.
О т в е т: сходится.
П р и м е р 20. Исследовать на сходимость ряд:
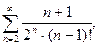 где
где 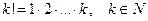 .
.
Р е ш е н и е. В данном случае 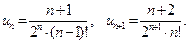 Поэтому получаем:
Поэтому получаем:
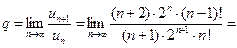
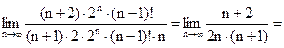
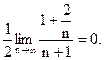
Следовательно, воспользовавшись признаком Даламбера, где 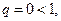 заключаем: ряд сходится.
заключаем: ряд сходится.
О т в е т: сходится.
П р и м е р 21. Исследовать на сходимость ряд: 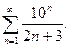
Р е ш е н и е. В данном случае 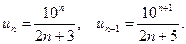 Поэтому получаем:
Поэтому получаем:
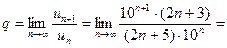

Следовательно, по признаку Даламбера ряд расходится, так как 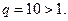
О т в е т: расходится.
П р и м е р 22. Исследовать сходимость ряда: 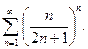
Р е ш е н и е. Для данного ряда  . Вычислим предел:
. Вычислим предел:
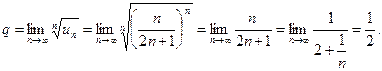
Следовательно, так как 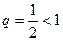 , то по радикальному признаку Коши изучаемый в примере ряд сходится.
, то по радикальному признаку Коши изучаемый в примере ряд сходится.
О т в е т: сходится.
П р и м е р 23. Исследовать сходимость ряда: 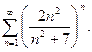
Р е ш е н и е. В данном случае
 , откуда
, откуда 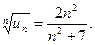
Вычислим предел: 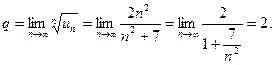
Следовательно, по радикальному признаку Коши рассматриваемый в примере ряд расходится.
О т в е т: расходится.
ПРИМЕРЫ
Найти общий член ряда:
1. 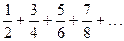 . 2.
. 2. 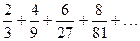 . 3.
. 3. 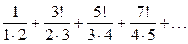 .
.
4. 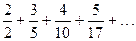 . 5.
. 5. 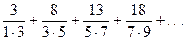 . 6.
. 6. 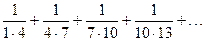 .
.
7. 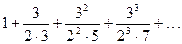 . 8.
. 8. 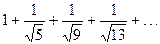 .
.
Исследовать на сходимость, исходя из определения, и найти сумму:
9. 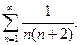 10.
10. 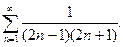 11.
11. 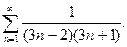 12.
12. 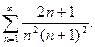
Проверить выполнение необходимого условия сходимости ряда:
13. 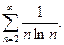 14.
14. 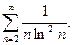 15.
15. 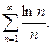 16.
16. 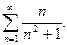
17. 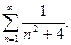 18.
18. 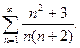 19.
19. 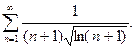 20.
20. 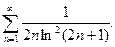
21. 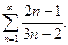 22.
22. 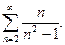 23.
23. 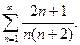 24.
24. 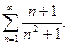
25. 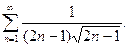 26.
26. 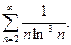 27.
27. 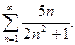 28.
28. 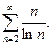
Исследовать на сходимость по интегральному признаку Коши:
29. 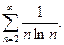 30.
30. 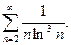 31.
31. 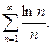 32.
32. 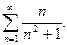 33.
33. 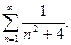 34.
34. 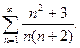
35. 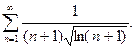 36.
36. 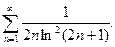 37.
37. 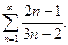 38.
38. 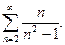 39.
39. 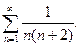
40. 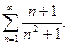 41.
41. 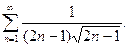 42.
42. 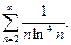 43.
43. 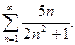 44.
44. 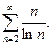
Исследовать ряды на сходимость по признакам сравнения:
45. 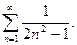 46.
46. 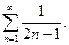 47.
47. 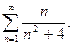 48.
48. 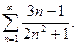 49.
49. 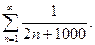
50. 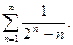 51.
51. 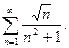 52.
52. 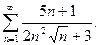 53.
53. 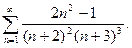
54. 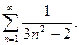 55.
55. 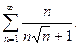 56.
56. 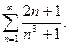 57.
57. 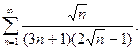
58. 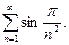 59.
59. 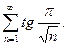 60.
60. 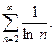 61.
61. 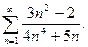
Исследовать ряды на сходимость по признаку Даламбера:
62. 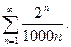 63.
63. 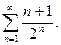 64.
64. 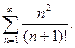 65.
65. 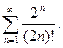 66.
66. 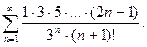
67. 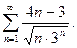 68.
68. 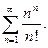 69.
69. 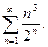 70.
70. 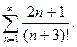 71.
71. 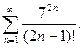 72.
72. 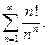
73. 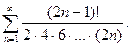 74.
74. 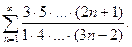 75.
75.  76.
76. 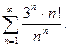
Исследовать сходимость рядов с помощью радикального признака Коши:
77. 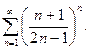 78.
78. 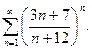 79.
79. 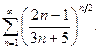 80.
80. 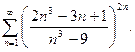
81. 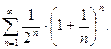 82.
82. 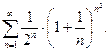 83.
83. 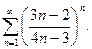 84.
84. 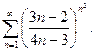
ОТВЕТЫ
1. 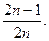 2.
2. 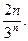 3.
3. 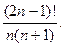 4.
4. 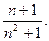 5.
5. 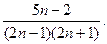 6.
6. 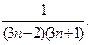
7. 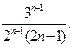 8.
8. 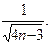 9. сходится;
9. сходится; 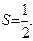 10. сходится;
10. сходится; 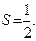 11. сходится;
11. сходится; 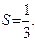
12. сходится; 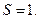 13. выполняется. 14. выполняется. 15. выполняется.
13. выполняется. 14. выполняется. 15. выполняется.
16. выполняется. 17. выполняется. 18. невыполняется, расходится.
19. выполняется. 20. выполняется. 21. не выполняется, расходится.
22. выполняется. 23. выполняется. 24. выполняется. 25. выполняется.
26. выполняется. 27. выполняется. 28. не выполняется, расходится.
29. расходится. 30. сходится. 31. расходится. 32. расходится.
33. сходится. 34. расходится. 35. расходится. 36. сходится.
37. расходится. 38. расходится. 39. сходится. 40. расходится.
41. сходится. 42. сходится. 43. расходится. 44. расходится.
45. сходится. 46. расходится. 47. расходится. 48. расходится.
49. расходится. 50. сходится. 51. сходится. 52. сходится.
53. сходится. 54. сходится. 55. расходится. 56. сходится.
57. расходится. 58. сходится. 59. расходится. 60. расходится.
61. сходится. 62. расходится. 63. сходится. 64. сходится.
65. сходится. 66. сходится. 67. сходится. 68. расходится.
69. сходится. 70. сходится. 71. сходится. 72. сходится.
73. расходится. 74. сходится. 75. сходится. 76. расходится.
77. сходится. 78. расходится. 79. сходится. 80. расходится.
81. сходится. 82. расходится. 83. сходится. 84. сходится.



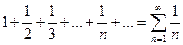 (10)
(10)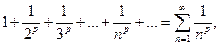 где
где 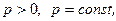 (11)
(11)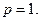
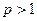 и расходится при
и расходится при 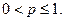
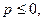 также является расходящимся. Но в этом случае для него не выполнено необходимое условие сходимости, так как
также является расходящимся. Но в этом случае для него не выполнено необходимое условие сходимости, так как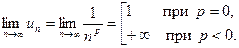
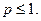
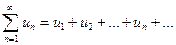 (12)
(12)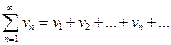 (13)
(13)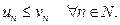 (14)
(14) (так как отбрасывание или приписывание к ряду любого конечного числа первых членов не меняет характер сходимости ряда).
(так как отбрасывание или приписывание к ряду любого конечного числа первых членов не меняет характер сходимости ряда).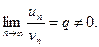 (15)
(15)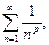 который сходится, если
который сходится, если 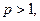 и расходится, если
и расходится, если 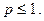
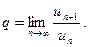 (16)
(16)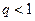 ряд (7) сходится, при
ряд (7) сходится, при 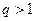 ряд (7) расходится. При
ряд (7) расходится. При 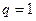 вопрос о сходимости или расходимости ряда (7) остается нерешенным.
вопрос о сходимости или расходимости ряда (7) остается нерешенным.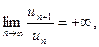
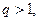 ряд (7) расходится.
ряд (7) расходится.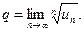 (17)
(17)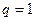 вопрос о сходимости ряда (7) остается нерешенным.
вопрос о сходимости ряда (7) остается нерешенным.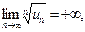 то, как и при
то, как и при 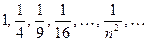 .
.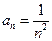 . Придавая числу
. Придавая числу 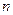 разные значения из множества натуральных чисел, находим члены последовательности. Например,
разные значения из множества натуральных чисел, находим члены последовательности. Например,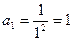 ,
, 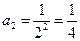 ,
, 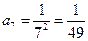 .
.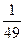 .
.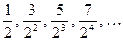 . (18)
. (18)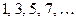 , у которой первый член
, у которой первый член 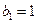 и разность
и разность 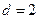 .
.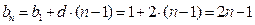 .
.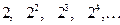 , у которой
, у которой 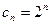 . Следовательно, общий член последовательности (18) задается формулой:
. Следовательно, общий член последовательности (18) задается формулой: 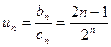 . Поэтому заключаем:
. Поэтому заключаем: 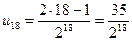 .
.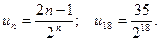
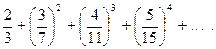
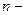 го члена равен
го члена равен 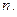 Числители дробей
Числители дробей 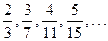 образуют арифметическую прогрессию, где
образуют арифметическую прогрессию, где 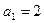 и
и 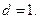 Поэтому
Поэтому 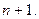 Знаменатели указанных дробей образуют арифметическую прогрессию с
Знаменатели указанных дробей образуют арифметическую прогрессию с 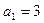 и
и 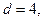 поэтому
поэтому 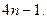 Тогда общим членом ряда является
Тогда общим членом ряда является 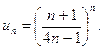
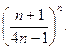
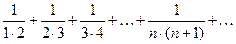 . (19)
. (19)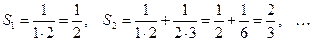 ,
,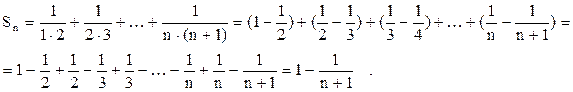
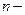 я частичная сумма ряда (8) вычисляется по формуле:
я частичная сумма ряда (8) вычисляется по формуле: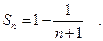
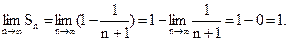 Значит, ряд (19) сходится и его сумма
Значит, ряд (19) сходится и его сумма 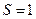 .
.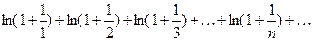 . (20)
. (20)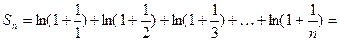
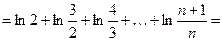
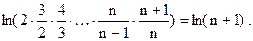
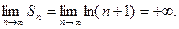 Поэтому ряд (20) расходится.
Поэтому ряд (20) расходится.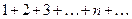 .. (21)
.. (21)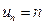 , откуда находим:
, откуда находим: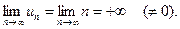
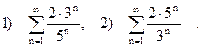
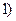 В этом случае ряд составлен из членов геометрической прогрессии, где
В этом случае ряд составлен из членов геометрической прогрессии, где 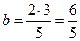 и
и 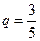 . Так как
. Так как 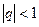 , то по теореме 2 ряд сходится и его сумма вычисляется по формуле:
, то по теореме 2 ряд сходится и его сумма вычисляется по формуле: 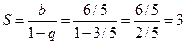 .
.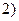 В этом случае ряд составлен из членов геометрической прогрессии, где
В этом случае ряд составлен из членов геометрической прогрессии, где 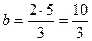 и
и 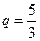 . Так как
. Так как 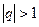 , то по теореме 2 ряд расходится.
, то по теореме 2 ряд расходится.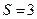 ;
; 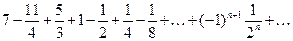 . (22)
. (22)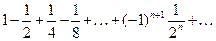 , (23)
, (23)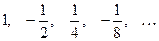 с первым членом
с первым членом 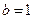 и знаменателем
и знаменателем 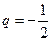 , значит,
, значит, 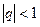 . Следовательно, по теореме 2 ряд (23) сходится и имеет сумму
. Следовательно, по теореме 2 ряд (23) сходится и имеет сумму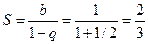 .
.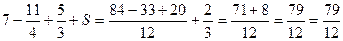 .
.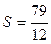 .
.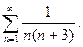
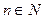 справедливо равенство:
справедливо равенство: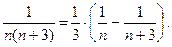

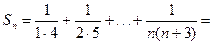
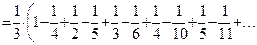
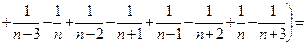
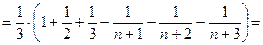
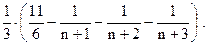
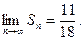
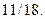
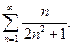
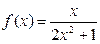 при
при 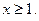 Она непрерывна на
Она непрерывна на 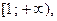 положительна и монотонно убывает (
положительна и монотонно убывает (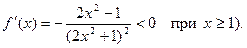 Поэтому интегральный признак Коши применим к рассматриваемому ряду.
Поэтому интегральный признак Коши применим к рассматриваемому ряду.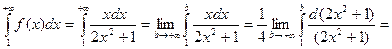
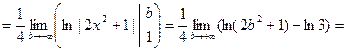
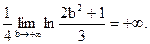
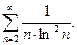
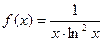 ,
, 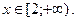 Она непрерывна при
Она непрерывна при 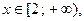 положительна, монотонно убывает (так как
положительна, монотонно убывает (так как 
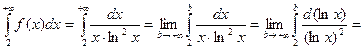
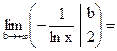
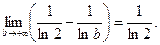
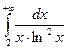 сходится. Значит, по интегральному признаку Коши сходится рассматриваемый в примере ряд.
сходится. Значит, по интегральному признаку Коши сходится рассматриваемый в примере ряд.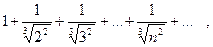 б)
б) 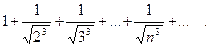
 . Он расходится как ряд Дирихле с показателем
. Он расходится как ряд Дирихле с показателем 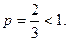 Ряд б) совпадает со следующим:
Ряд б) совпадает со следующим: 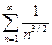 . Он сходится как ряд Дирихле с показателем
. Он сходится как ряд Дирихле с показателем 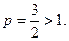
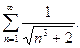
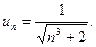
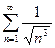 с общим членом
с общим членом 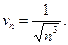 Нетрудно видеть, что
Нетрудно видеть, что 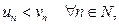 так как
так как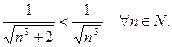
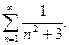
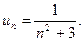 Рассмотрим вспомогательный ряд
Рассмотрим вспомогательный ряд 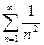 , для которого
, для которого 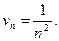 Так как
Так как 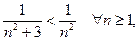 то есть
то есть 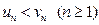 . Следовательно, выполнены условия первого признака сравнения рядов.
. Следовательно, выполнены условия первого признака сравнения рядов.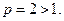 Следовательно, он сходится. Тогда по первому признаку сравнения будет сходиться и данный в примере ряд.
Следовательно, он сходится. Тогда по первому признаку сравнения будет сходиться и данный в примере ряд.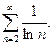 (24)
(24)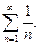 На рис. 1 даны графики функций
На рис. 1 даны графики функций 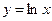 и
и 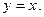 Очевидно, что
Очевидно, что 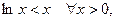 в частности, при
в частности, при 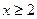 , где
, где 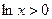 . Тогда
. Тогда 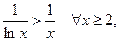 откуда заключаем:
откуда заключаем: 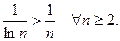

 у
у у = lnx
у = lnx

 1
1 О 1 е х
О 1 е х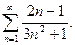
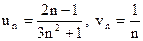 , откуда получаем
, откуда получаем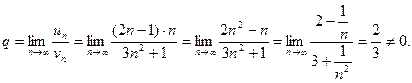
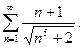 (25)
(25)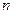 удовлетворяет приближенному равенству:
удовлетворяет приближенному равенству: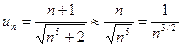 .
.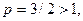 а значит, сходящийся. Его общий член задается формулой:
а значит, сходящийся. Его общий член задается формулой: 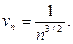
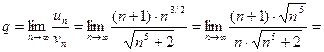

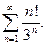
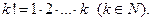 Для данного ряда
Для данного ряда 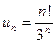 и
и 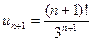 .
.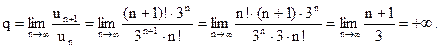
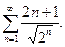
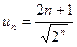 и
и 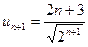 . Поэтому получаем:
. Поэтому получаем: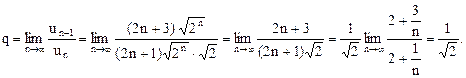
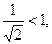 то по признаку Даламбера заключаем: рассматриваемый ряд сходится.
то по признаку Даламбера заключаем: рассматриваемый ряд сходится.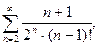 где
где 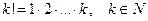 .
.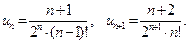 Поэтому получаем:
Поэтому получаем: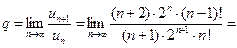
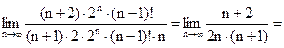
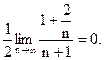
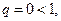 заключаем: ряд сходится.
заключаем: ряд сходится.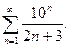
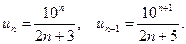 Поэтому получаем:
Поэтому получаем: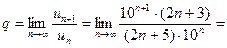

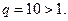
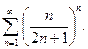
 . Вычислим предел:
. Вычислим предел: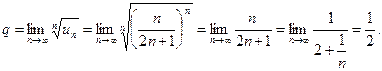
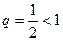 , то по радикальному признаку Коши изучаемый в примере ряд сходится.
, то по радикальному признаку Коши изучаемый в примере ряд сходится.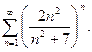
 , откуда
, откуда 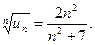
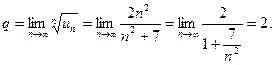
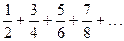 . 2.
. 2. 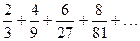 . 3.
. 3. 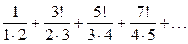 .
.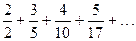 . 5.
. 5. 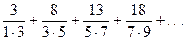 . 6.
. 6. 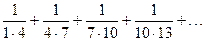 .
.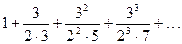 . 8.
. 8. 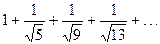 .
.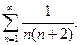 10.
10. 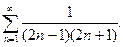 11.
11. 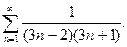 12.
12. 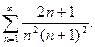
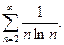 14.
14. 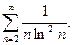 15.
15. 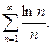 16.
16. 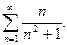
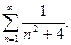 18.
18. 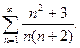 19.
19. 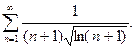 20.
20. 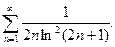
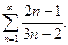 22.
22. 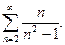 23.
23. 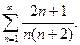 24.
24. 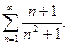
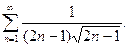 26.
26. 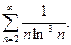 27.
27. 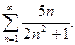 28.
28. 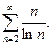
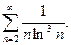 31.
31. 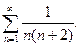
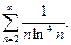 43.
43. 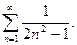 46.
46. 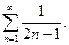 47.
47. 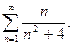 48.
48. 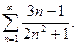 49.
49. 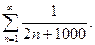
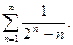 51.
51. 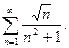 52.
52. 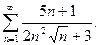 53.
53. 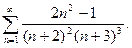
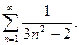 55.
55. 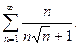 56.
56. 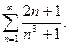 57.
57. 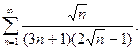
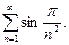 59.
59. 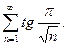 60.
60. 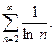 61.
61. 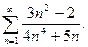
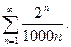 63.
63. 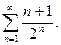 64.
64. 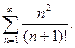 65.
65. 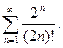 66.
66. 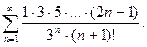
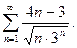 68.
68. 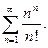 69.
69. 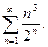 70.
70. 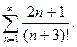 71.
71. 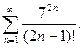 72.
72. 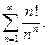
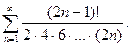 74.
74. 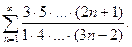 75.
75.  76.
76. 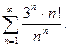
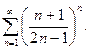 78.
78. 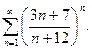 79.
79. 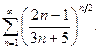 80.
80. 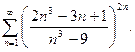
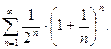 82.
82. 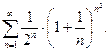 83.
83. 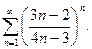 84.
84. 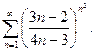
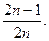 2.
2. 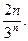 3.
3. 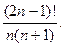 4.
4. 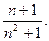 5.
5. 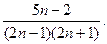 6.
6. 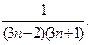
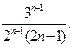 8.
8. 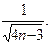 9. сходится;
9. сходится; 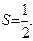 10. сходится;
10. сходится; 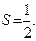 11. сходится;
11. сходится; 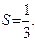
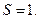 13. выполняется. 14. выполняется. 15. выполняется.
13. выполняется. 14. выполняется. 15. выполняется.


