Опыт показывает, что внутренняя энергия идеального газа зависит только от температуры:

Здесь В — коэффициент пропорциональности, который остается постоянным в весьма широком интервале температур.
Отсутствие зависимости внутренней энергии от занимаемого газом объема указывает на то, что молекулыидеального газа подавляющую часть времени не взаимодействуют друг с другом. Действительно, если бы молекулы взаимодействовали между собой, во внутреннюю энергию входила бы слагаемым потенциальная энергия взаимодействия, которая зависела бы от среднего расстояния между молекулами, т. е. от  .
.
Отметим, что взаимодействие должно иметь место при столкновениях, т. е. при сближении молекул на очень малое расстояние. Однако такие столкновения в разреженном газе происходят редко. Подавляющую часть времени каждая молекула проводит в свободном полете.
Теплоемкостью какого-либо тела называется величина, равная количеству тепла, которое нужно сообщить телу, чтобы повысить его температуру на один кельвин. Если сообщение телу количества тепла  повышает его температуру на
повышает его температуру на  то теплоемкость по определению равна
то теплоемкость по определению равна

Эта величина измеряется в джоулях на кельвин (Дж/К).
Теплоемкость моля вещества, называемую молярной теплоемкостью, мы будем обозначать прописной буквой С. Измеряется она в джоулях на моль-кельвин (Дж/(моль•К)).
Теплоемкость единицы массы вещества называется удельной теплоемкостью. Ее мы будем обозначать строчной буквой с. Измеряется с в джоулях на килограмм-кельвин 
Между молярной и удельной теплоемкостями одного и того же вещества имеется соотношение

( — молярная масса).
— молярная масса).
Величина теплоемкости зависит от условий, при которых происходит нагревание тела. Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или при постоянном давлении. В первом случае теплоемкость называется теплоемкостью при постоянном объеме (обозначается  ), во втором — теплоемкостью при постоянном давлении
), во втором — теплоемкостью при постоянном давлении 
Если нагревание происходит при постоянном объеме, тело не совершает работы над внешними телами и, следовательно, согласно первому началу термодинамики (см. (83.4)), все тепло идет на приращение внутренней энергии тела:

Из (87.4) вытекает, что теплоемкость любого тела при постоянном объеме равна

Такая запись подчеркивает то обстоятельство, что при дифференцировании выражения для U по Т объем следует считать постоянным. В случае идеального газа U зависит только от Т, так что выражение (87.5) можно представить в виде

(чтобы получить молярную теплоемкость, нужно взять внутреннюю энергию моля газа).
Выражение (87.1) для одного моля газа имеет вид  Продифференцировав его по Т, получим, что
Продифференцировав его по Т, получим, что  Таким образом, выражение для внутренней энергии одного моля идеального газа можно представить в виде
Таким образом, выражение для внутренней энергии одного моля идеального газа можно представить в виде

где  — молярная теплоемкость газа при постоянном объеме.
— молярная теплоемкость газа при постоянном объеме.
Внутренняя энергия произвольной массы газа  будет равна внутренней энергии одного моля, умноженной на число молей газа, содержащихся в массе
будет равна внутренней энергии одного моля, умноженной на число молей газа, содержащихся в массе  :
:

Если нагревание газа происходит при постоянном давлении, то газ будет расширяться, совершая над внешними телами положительную работу. Следовательно, для повышения температуры газа на один кельвин в этом случае понадобится больше тепла, чем при нагревании при постоянном объеме, — часть тепла будет затрачиваться на совершение газом работы. Поэтому теплоемкость при постоянном давлении должна быть больше, чем теплоемкость при постоянном объеме.
Напишем уравнение (84.4) первого начала термодинамики для моля газа:

В этом выражении индекс  при
при  указывает на то, что тепло сообщается газу в условиях, когда
указывает на то, что тепло сообщается газу в условиях, когда  постоянно. Разделив (87.8) на
постоянно. Разделив (87.8) на  получим выражение для молярной теплоемкости газа при постоянном давлении:
получим выражение для молярной теплоемкости газа при постоянном давлении:
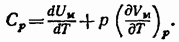
Слагаемое  равно, как мы видели, молярной теплоемкости при постоянном объеме. Поэтому формула (87.9) может быть написана следующим образом:
равно, как мы видели, молярной теплоемкости при постоянном объеме. Поэтому формула (87.9) может быть написана следующим образом:
 (87.10)
(87.10)
Величина  представляет собой приращение объема моля газа при повышении температуры на один кельвин, получающееся в случае, когда
представляет собой приращение объема моля газа при повышении температуры на один кельвин, получающееся в случае, когда  постоянно. В соответствии с уравнением состояния (86.3)
постоянно. В соответствии с уравнением состояния (86.3)  . Дифференцируя это выражение по Т, полагая р=const, находим
. Дифференцируя это выражение по Т, полагая р=const, находим

Наконец, подставив этот результат в (87.10), получаем
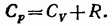 (87.11)
(87.11)
Таким образом, работа, которую совершает моль идеального газа при повышении его температуры на один кельвин при постоянном давлении, оказывается равной газовой постоянной R.
Отметим, что соотношение (87.11) получено с использованием уравнения состояния идеального газа и, следовательно, справедливо только для идеального газа.
Величина
 (87.12)
(87.12)
представляет собой характерную для каждого газа величину. Для одноатомных газов это отношение близко к 5/3, для двухатомных — к 7/5, для трехатомных — к 4/3 и т. д. В дальнейшем (см. § 97) мы увидим, что значение у определяется числом и характером степеней свободы молекулы.
В соответствии с (87.11)
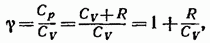
откуда
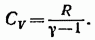 (87.13)
(87.13)
Подставив это значение  в формулу (87.7), получим следующее выражение:
в формулу (87.7), получим следующее выражение:

Сопоставление с (86.4) дает еще одно выражение для внутренней энергии идеального газа:

Вопрос №63
Адиабатический процесс - это такое изменение состояний газа, при котором он не отдает и не поглощает извне теплоты. Следовательно, адиабатический процесс характеризуется отсутствием теплообмена газа с окружающей средой. Адиабатическими можно считать быстро протекающие процессы. Так как передачи теплоты при адиабатическом процессе не происходит, то  и уравнение I начала термодинамики принимает вид
и уравнение I начала термодинамики принимает вид

| (9.20)
|
или

т.е. внешняя работа газа может производиться вследствие изменения его внутренней энергии. Адиабатное расширение газа (dV>0) сопровождается положительной внешней работой, но при этом внутренняя энергия уменьшается и газ охлаждается (dT<0).
Сжатие газа (dV0, т.е. адиабатное сжатие газа сопровождается его нагреванием.
Найдем связь между параметрами состояния идеального газа (например, Р и V) в адиабатическом процессе. Для этого перепишем (9.20) в форме

а величину 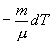 найдем из уравнения Менделеева - Клапейрона
найдем из уравнения Менделеева - Клапейрона

Таким образом,

или, учитывая, что для идеального газа 

Разделим обе части этого уравнения на 

где  безразмерная величина, называемая постоянной адиабаты. Пренебрегая зависимостью
безразмерная величина, называемая постоянной адиабаты. Пренебрегая зависимостью  от температуры, можно считать, что для данного газа
от температуры, можно считать, что для данного газа  . Интегрируя последнее уравнение
. Интегрируя последнее уравнение

получим

т.е.

| (9.21)
|
Это выражение называют уравнением Пуассона. Соотношение между давлением и температурой, а также между объемом и температурой идеального газа в адиабатическом процессе имеют вид

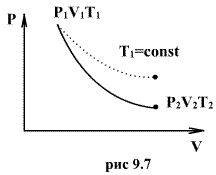
Эти соотношения легко получить из (9.21), пользуясь уравнением Менделеева - Клапейрона. Линию, изображающую адиабатический процесс в диаграмме состояния, называют адиабатой. На рис. 9.7 сплошной линией показан вид адиабаты в (P-V) диаграмме. Для сравнения в том же рисунке пунктирной линией изображена изотерма, соответствующая температуре газа в начальном состоянии 1. Так как для любого идеального газа показатель адиабаты  , то в (P-V) диаграмме адиабата всегда идет круче, чем изотерма. Объясняется это тем, что при адиабатическом сжатии увеличение давления обусловлено не только уменьшением объема газа, как при изотермическом сжатии, то также еще и увеличения температуры. При адиабатическом расширении температура газа уменьшается, поэтому давление газа падает быстрее, чем при изотермическом расширении.
, то в (P-V) диаграмме адиабата всегда идет круче, чем изотерма. Объясняется это тем, что при адиабатическом сжатии увеличение давления обусловлено не только уменьшением объема газа, как при изотермическом сжатии, то также еще и увеличения температуры. При адиабатическом расширении температура газа уменьшается, поэтому давление газа падает быстрее, чем при изотермическом расширении.
Работу, совершаемую газом в адиабатическом процессе, найдем интегрируя выражение

Полная работа

Из уравнения Майера (9.18) и выражения  для показателя адиабаты γ следует, что
для показателя адиабаты γ следует, что

Поэтому

| (9.22)
|
В соответствии с соотношением 

Следовательно, выражение (9.22) для работы можно представить в виде

или
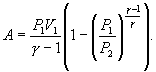
Вопрос №64
Анализируя работу тепловых двигателей, французский инженер С. Карно в 1824г. пришел к выводу, что наивыгоднейшим круговым процессом является обратимый круговой процесс, состоящий из двух изотермических и двух адиабатических процессов, т.к. он характеризуется наибольшим коэффициентом полезного действия. Такой цикл получил название цикла Карно. В прямом цикле Карно рабочее тело изотермически, а затем адиабатически расширяется, после чего снова изотермически (при более низкой температуре) и потом адиабатически сжимается. Т.е. цикл Карно ограничен двумя изотермами и двумя адиабатами.
При изотермическом расширении от нагревателя отбирается тепло  (на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны
(на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны  . На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т2. Параметры точки 3 -
. На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т2. Параметры точки 3 -  . На участке 3-4 газ изотермически сжимается. Параметры точки 4 -
. На участке 3-4 газ изотермически сжимается. Параметры точки 4 - 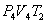 . Выделяющееся при этом тепло
. Выделяющееся при этом тепло  отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту
отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту  , а холодильник отобрал
, а холодильник отобрал  Разность
Разность  определяет полезную работу газа за один цикл, так как согласно I началу термодинамики
определяет полезную работу газа за один цикл, так как согласно I началу термодинамики  , но для кругового процесса
, но для кругового процесса  и, следовательно
и, следовательно  .
.

Отношение полезной работы к затраченной энергии нагревателя определяет коэффициент полезного действия (к.п.д.) тепловой машины:

| (9.23)
|
Эта формула справедлива для любого обратимого и необратимого процесса.
Определим коэффициент полезного действия цикла Карно для обратимого процесса. Теплота подводится на участке 1-2 и отводится на участке 3-4. Для изотермического процесса внутренняя энергия Q=const и все подводимое тепло расходуется на работу  .
.
Тогда
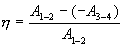
или

Для изотермического процесса работа


С учетом последних выражений
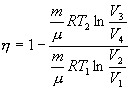
| (9.24)
|
Покажем, что

Так как процессы на участках 2-3 и 1-4 адиабатические, для определения связи между  и
и  и
и  и
и  используем уравнение Пуассона в виде
используем уравнение Пуассона в виде 
Следовательно,

и

Разделим эти уравнения и получим

Тогда выражение для к.п.д. (9.24) примет вид

Эта формула справедлива только для обратимого цикла Карно.
Теоремы Карно.
- Все обратимые машины, работающие по циклу Карно, имеют, независимо от природы рабочего тела, одинаковый КПД при условии если у них общий нагреватель и холодильник.
- Если две тепловые машины имеют общий нагреватель и холодильник и одна обратимая, а другая необратимая, то КПД обратимой больше необратимой

Вопрос №65
Рассмотрим обратимый и необратимый циклы Карно
Обратимый цикл Карно. Для обратимого цикла коэффициент полезного действия можно вычислить по любой из полученных ранее формул

Отсюда
 или
или 
 - количество тепла, подводимое к системе в процессе перехода из состояния 1 в состояние 2.
- количество тепла, подводимое к системе в процессе перехода из состояния 1 в состояние 2.  - отведенное тепло в течение изотермического процесса 3-4. Или для случая отвода тепла можно сказать, что к системе подведено
- отведенное тепло в течение изотермического процесса 3-4. Или для случая отвода тепла можно сказать, что к системе подведено  тепла. Тогда
тепла. Тогда

| (9.25)
|
Отношение количества теплоты, подведенной к системе, к температуре, при которой это происходит, называется приведенной теплотой. Таким образом,  - приведенная теплота, передаваемая системе.
- приведенная теплота, передаваемая системе. 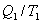 - приведенная теплота в 1 процессе.
- приведенная теплота в 1 процессе.  - приведенная теплота во II процессе. На участках 2-3 и 4-1 Q=0. Следовательно, это вся теплота охватывающая цикл Карно. Таким образом, для обратимого цикла Карно
- приведенная теплота во II процессе. На участках 2-3 и 4-1 Q=0. Следовательно, это вся теплота охватывающая цикл Карно. Таким образом, для обратимого цикла Карно

| (9.26)
|
Так как любой замкнутый цикл можно представить как сумму бесконечного числа циклов Карно, то для любого замкнутого обратимого цикла выражение (9.26) будет справедливо и его можно записать в следующем виде

| (9.27)
|
Последнее соотношение носит название равенства Клаузиуса.
Необратимый цикл Карно. В этом случае

И все равенства превращаются в неравенства
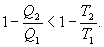
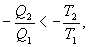







| (9.28)
|
Уравнение (9.28) называется неравенством Клаузиуса.
Объединяя (9.27) и (9.28), получим

| (9.29)
|
Таким образом, сумма приведенных теплот любого цикла равна нулю (обратимый процесс) или меньше нуля (необратимый процесс).
Вопрос №66
равнение Ван–дер–Ваальса (7.1.2) – одно из первых уравнений состояния реального газа. Данное уравнение учитывает конечные размеры всех молекул, что становится существенным при больших давлениях, а также притяжение молекул в результате межмолекулярного взаимодействия.
Уравнение состояния реального газа, предложенное Ван–дер–Ваальсом можно получить из следующих рассуждений. Учтем влияние конечных размеров молекул на уравнение состояния реального газа. Давление определяется средней кинетической энергией теплового движения всех молекул Р = nkT. 7.2.1 При конечных размерах молекул, имеющих радиус r, область 4p(2r)3/3 вокруг каждой из молекул будет недоступна для попадания в нее другой неточечной молекулы. В результате в сосуде, содержащем N молекул конечных размеров, область объемом (N/2)4p(2r)3/3 = 4NVмолек (Vмолек = 4pr3/3 – объем одной молекулы) будет недоступна для столкновений. Поэтому можно считать, что половина всех молекул занимает объем b = 4NVмолек и покоится, а другая половина представляет собой точечные молекулы и движется с удвоенной кинетической энергией, обладая температурой Т´ = 2Т. Объем, доступный точечным молекулам, будет равен V - b, а давление, оказываемое на стенки сосуда, определяется точечными подвижными молекулами (N´ = N/2):
Р = n´kT´ = 
Если в сосуде находится один моль газа, то уравнение состояния примет вид (N = NA, NAk = R, b = 4NAVмолек):
P(V - b) = RT.
Для v = m/m молей газа уравнение состояния газа с учетом конечного размера молекул примет вид
P(V - nb) = nRT.
Отметим, что это уравнение является приближенным и выведено в предположении только парных столкновений. При больших давлениях это условие уже не выполняется, и возможно одновременное соприкосновение трех и более частиц, а такие случаи были исключены из рассмотрения.
Рассмотрим теперь влияние сил притяжения на уравнение состояния идеального газа. Будем считать для простоты частицы газа точечными. Наличие сил притяжения между ними, действующих на больших расстояниях, приводит к появлению дополнительного внутреннего воздействия на газ. Это обусловлено тем, что в то время как в объеме газа действие сил притяжения между молекулами в среднем уравновешивается, на границе «газ – стенка сосуда» действие сил притяжения со стороны газа остается не скомпенсированным, и появляется избыточная сила, направленная в сторону газа (рис. 7.3).

Рис. 7.3
Дополнительное внутреннее давление пропорционально числу частиц, приходящихся на единицу площади границы nS и силе взаимодействия этих частиц с другими частицами газа, находящимися в единице объема nV.
В результате избыточное внутреннее давление Pi (i - intrinsic) будет пропорционально квадрату концентрации числа частиц
Pi ~ nS nV ~ N 2/V 2,
где N – полное число частиц в сосуде объема V. Если N = NA – в сосуде находится один моль газа, то запишем
Pi = a/V 2,
где а – постоянная величина, своя для каждого сорта газа. В случае v -молей имеем
Pi = v2a/V 2.
С учетом внутреннего давления уравнение состояния примет вид
P + Pi = nkT.
Давление Pi не зависит от материала стенки, в противном случае удалось бы создать вечный двигатель первого рода. Роль стенки может играть и сам газ. Достаточно для этого выполнить мысленное сечение произвольной плоскостью любой внутренней области объема газа. Полученное уравнение, с учетом выражения для Pi переходит в новое уравнение состояния реального газа при наличии сил притяжения:
(P + v2 a/V 2)V = vRT.
Учитывая совместное действие сил притяжения и сил отталкивания и полученные поправки для объема и давления в уравнении Менделеева – Клапейрона, получим уравнение Ван–дер–Ваальса для реального газа:
(P + v2 a/V 2)(V - vb) = vRT, (7.2.3)
или для одного моля:
|
|  . .
|
| 7.2.4
|
Данное уравнение справедливо при условии vb << V и v2a/V 2 << P. Помимо этого предполагается, что частицы газа сферически симметричны. Поскольку реально это не так, то даже для неплотных газов величины а и b зависят от температуры. Константы Ван–дер–Ваальса и критические данные приведены в таблице 7.1
Таблица 7.1.
|
| Pk, атм
| Vk, м3/кмоль
| Тk, К
| а, ат×м6/кмоль2
| b, м3/кмоль
| R / NAk
|
| HCl H2 He H2O O2 N2 CO2
| 86 13,2 2,34 225 51,4 34,8 75
| 0,060 0,065 0,058 0,055 0,075 0,090 0,096
| 324,6 33,2 5,2 647,3 154,3 126,0 304,1
| 0,922 0,194 0,035 5,65 1,40 1,39 3,72
| 0,020 0,022 0,024 0,031 0,032 0,039 0,043
| 0,469 0,813 0,821 0,602 0,768 0,782 0,745
|
Примечание. Константы а и b выбраны таким образом, чтобы получить оптимальное согласование уравнения Ван–дер–Ваальса с измеренными изотермами для комнатной температуры. Для плотных газов уравнение Ван–дер–Ваальса как количественное соотношение не годится. Однако качественно оно позволяет описывать поведение газов при высоких давлениях, конденсацию газов и переход газов в критическое состояние.
Вопрос №67
ассмотрим поверхность жидкости, опирающуюся на некоторый плоский контур (рис. 314, а). Если поверхность жидкости не плоская, то стремление её к сокращению приведет к возникновению давления, дополнительного к тому, которое испытывает жидкость с плоской поверхностью. В случае выпуклой поверхности это дополнительное давление положительно (рис. 314, б), в случае вогнутой поверхности – отрицательно (рис. 314, в). В последнем случае поверхностный слой, стремясь сократиться, растягивает жидкость.
Величина добавочного давления, очевидно, должна возрастать с увеличением коэффициента поверхностного натяжения  и кривизны поверхности. Вычислим добавочное давление для сферической поверхности жидкости. Для этого рассечем мысленно сферическую каплю Жидкости диаметральной плоскостью на два полушария (рис. 315).
и кривизны поверхности. Вычислим добавочное давление для сферической поверхности жидкости. Для этого рассечем мысленно сферическую каплю Жидкости диаметральной плоскостью на два полушария (рис. 315).
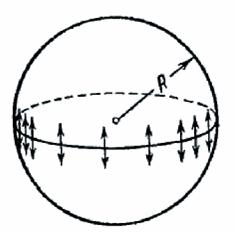
Рис. 315.
Из-за поверхностного натяжения оба полушария притягиваются друг к другу с силой, равной

Эта сила прижимает друг к другу оба полушария по поверхности  и, следовательно обусловливается дополнительное давление
и, следовательно обусловливается дополнительное давление
|
| 
| (144.1)
|
Кривизна сферической поверхности всюду одинакова и определяется радиусом сферы R. Очевидно, что чем меньше R, тем больше кривизна сферической поверхности. Кривизну произвольной поверхности принято характеризовать так называемой средней кривизной, которая может оказаться различной для разных точек поверхности.
Средняя кривизна определяется через кривизну нормальных сечений. Нормальные сечением поверхности в некоторой точке называется линия пересечения этой поверхности с плоскостью, проходящей через нормаль к поверхности в рассматриваемой точке. Для сферы любое нормальное сечение представляет собой окружность радиуса R (R — радиус сферы). Величина H=1/R дает кривизну сферы. В общем случае различные нормальные сечения, проведенные через одну и ту же точку, имеют различную кривизну. В геометрии доказывается, что полусумма обратных радиусов кривизны:
|
| 
| (144.2)
|
для любой пары взаимно-перпендикулярных нормальных сечений имеет одно и то же значение. Эта величина и есть средняя кривизна поверхности в данной точке.
Радиусы R1 и R2 в формуле (144.2) — алгебраические величины. Если центр кривизны нормального сечения находится под данной поверхностью, соответствующий радиус кривизны положителен; если центр кривизны лежит над поверхностью, радиус кривизны отрицателен (рис. 316).

Рис. 316.
Таким образом, неплоская поверхность может иметь среднюю кривизну, равную нулю. Для этого нужно, чтобы радиусы кривизны R1 и R2 были одинаковы по величине и противоположны по знаку.
Для сферы  , и по формуле (144.2)
, и по формуле (144.2) 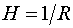 . Подставляя это значение в (144.1), получаем для добавочного давления под сферической поверхностью
. Подставляя это значение в (144.1), получаем для добавочного давления под сферической поверхностью
|
| 
| (144.3)
|
Как показал Лаплас, формула (144.3) справедлива для поверхности любой формы, если под Н понимать среднюю кривизну поверхности в той точке, под которой определяется дополнительное давление. Подставив в (144.3) выражение (144.2) для средней кривизны, получим формулу для добавочного давления под произвольной поверхностью:
|
| 
| (144.4)
|
Она называется формулой Лапласа.
Добавочное давление (144.4) обусловливает изменение уровня жидкости в узких трубках (капиллярах), вследствие чего называется иногда капиллярным давлением.
Рассмотрим поверхность, имеющую форму кругового цилиндра радиуса R. В качестве нормальных сечений возьмем сечение поверхности плоскостью, проходящей через ось цилиндра, и сечение плоскостью, перпендикулярной к оси {рис. 317).

Рис. 317.
Первым сечением будет прямая  вторым — окружность радиуса R*(R2=R). Кривизна цилиндрической поверхности по формуле (144.2) равна 1/2R, т. е. в 2 раза меньше, чем кривизна сферической поверхности того же радиуса. Дополнительное давление подцилиндрической поверхностью радиуса R согласно формуле (144.4) равно
вторым — окружность радиуса R*(R2=R). Кривизна цилиндрической поверхности по формуле (144.2) равна 1/2R, т. е. в 2 раза меньше, чем кривизна сферической поверхности того же радиуса. Дополнительное давление подцилиндрической поверхностью радиуса R согласно формуле (144.4) равно
|
| 
| (144.5)
|
Если в жидкости имеется пузырек газа, то поверхность пузырька, стремясь сократиться, будет оказывать на газ дополнительное давление. Повторяя рассуждения, приведшие нас к формуле (144.1), можно показать, что величина этого давления равна  . Найдем радиус пузырька в воде, при котором добавочное давление равно 1 aт. Коэффициент поверхностного натяжения воды при 20°С равен 0,073 н/м, 1 ат соответствует примерно 105 н/м2. Следовательно, для R получается следующее значение:
. Найдем радиус пузырька в воде, при котором добавочное давление равно 1 aт. Коэффициент поверхностного натяжения воды при 20°С равен 0,073 н/м, 1 ат соответствует примерно 105 н/м2. Следовательно, для R получается следующее значение:

Таким образом, Δp=lam при диаметре пузырька примерно 3 мк. Для пузырька диаметром 1 мм добавочное давление превышает 2 мм рт.ст.




 .
. повышает его температуру на
повышает его температуру на  то теплоемкость по определению равна
то теплоемкость по определению равна


 — молярная масса).
— молярная масса). ), во втором — теплоемкостью при постоянном давлении
), во втором — теплоемкостью при постоянном давлении 



 Продифференцировав его по Т, получим, что
Продифференцировав его по Т, получим, что  Таким образом, выражение для внутренней энергии одного моля идеального газа можно представить в виде
Таким образом, выражение для внутренней энергии одного моля идеального газа можно представить в виде
 — молярная теплоемкость газа при постоянном объеме.
— молярная теплоемкость газа при постоянном объеме. будет равна внутренней энергии одного моля, умноженной на число молей газа, содержащихся в массе
будет равна внутренней энергии одного моля, умноженной на число молей газа, содержащихся в массе  :
:

 при
при  указывает на то, что тепло сообщается газу в условиях, когда
указывает на то, что тепло сообщается газу в условиях, когда  постоянно. Разделив (87.8) на
постоянно. Разделив (87.8) на  получим выражение для молярной теплоемкости газа при постоянном давлении:
получим выражение для молярной теплоемкости газа при постоянном давлении: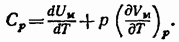
 равно, как мы видели, молярной теплоемкости при постоянном объеме. Поэтому формула (87.9) может быть написана следующим образом:
равно, как мы видели, молярной теплоемкости при постоянном объеме. Поэтому формула (87.9) может быть написана следующим образом: (87.10)
(87.10) представляет собой приращение объема моля газа при повышении температуры на один кельвин, получающееся в случае, когда
представляет собой приращение объема моля газа при повышении температуры на один кельвин, получающееся в случае, когда  постоянно. В соответствии с уравнением состояния (86.3)
постоянно. В соответствии с уравнением состояния (86.3)  . Дифференцируя это выражение по Т, полагая р=const, находим
. Дифференцируя это выражение по Т, полагая р=const, находим
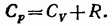 (87.11)
(87.11) (87.12)
(87.12)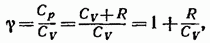
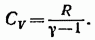 (87.13)
(87.13) в формулу (87.7), получим следующее выражение:
в формулу (87.7), получим следующее выражение:

 и уравнение I начала термодинамики принимает вид
и уравнение I начала термодинамики принимает вид


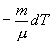 найдем из уравнения Менделеева - Клапейрона
найдем из уравнения Менделеева - Клапейрона





 безразмерная величина, называемая постоянной адиабаты. Пренебрегая зависимостью
безразмерная величина, называемая постоянной адиабаты. Пренебрегая зависимостью  от температуры, можно считать, что для данного газа
от температуры, можно считать, что для данного газа  . Интегрируя последнее уравнение
. Интегрируя последнее уравнение



 , то в (P-V) диаграмме адиабата всегда идет круче, чем изотерма. Объясняется это тем, что при адиабатическом сжатии увеличение давления обусловлено не только уменьшением объема газа, как при изотермическом сжатии, то также еще и увеличения температуры. При адиабатическом расширении температура газа уменьшается, поэтому давление газа падает быстрее, чем при изотермическом расширении.
, то в (P-V) диаграмме адиабата всегда идет круче, чем изотерма. Объясняется это тем, что при адиабатическом сжатии увеличение давления обусловлено не только уменьшением объема газа, как при изотермическом сжатии, то также еще и увеличения температуры. При адиабатическом расширении температура газа уменьшается, поэтому давление газа падает быстрее, чем при изотермическом расширении.


 для показателя адиабаты γ следует, что
для показателя адиабаты γ следует, что




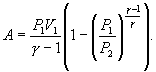
 (на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны
(на участке 1-2 рис. 9.11). Вследствие этого температура газа поддерживается неизменной. Соответственно, параметры точки 2 будут равны  . На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т2. Параметры точки 3 -
. На участке 2-3 происходит адиабатное расширение. Внутренняя энергия газа уменьшается и его температура падает до Т2. Параметры точки 3 -  . На участке 3-4 газ изотермически сжимается. Параметры точки 4 -
. На участке 3-4 газ изотермически сжимается. Параметры точки 4 - 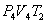 . Выделяющееся при этом тепло
. Выделяющееся при этом тепло  отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту
отбирается холодильником. Участок 4-1 -адиабатическое сжатие до исходного состояния, соответствующего точке 1. Таким образом, завершен цикл “1-2-3-4-1 и в итоге нагреватель отдал газу теплоту  определяет полезную работу газа за один цикл, так как согласно I началу термодинамики
определяет полезную работу газа за один цикл, так как согласно I началу термодинамики  , но для кругового процесса
, но для кругового процесса  и, следовательно
и, следовательно  .
.

 .
.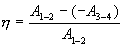



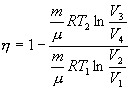

 и
и  и
и  используем уравнение Пуассона в виде
используем уравнение Пуассона в виде 






 или
или 
 тепла. Тогда
тепла. Тогда
 - приведенная теплота, передаваемая системе.
- приведенная теплота, передаваемая системе. 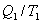 - приведенная теплота в 1 процессе.
- приведенная теплота в 1 процессе.  - приведенная теплота во II процессе. На участках 2-3 и 4-1 Q=0. Следовательно, это вся теплота охватывающая цикл Карно. Таким образом, для обратимого цикла Карно
- приведенная теплота во II процессе. На участках 2-3 и 4-1 Q=0. Следовательно, это вся теплота охватывающая цикл Карно. Таким образом, для обратимого цикла Карно


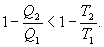
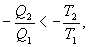









 .
.
 а)
а)
 б)
б)
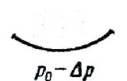 в)
в)
 и кривизны поверхности. Вычислим добавочное давление для сферической поверхности жидкости. Для этого рассечем мысленно сферическую каплю Жидкости диаметральной плоскостью на два полушария (рис. 315).
и кривизны поверхности. Вычислим добавочное давление для сферической поверхности жидкости. Для этого рассечем мысленно сферическую каплю Жидкости диаметральной плоскостью на два полушария (рис. 315).

 и, следовательно обусловливается дополнительное давление
и, следовательно обусловливается дополнительное давление


 , и по формуле (144.2)
, и по формуле (144.2) 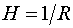 . Подставляя это значение в (144.1), получаем для добавочного давления под сферической поверхностью
. Подставляя это значение в (144.1), получаем для добавочного давления под сферической поверхностью


 вторым — окружность радиуса R*(R2=R). Кривизна цилиндрической поверхности по формуле (144.2) равна 1/2R, т. е. в 2 раза меньше, чем кривизна сферической поверхности того же радиуса. Дополнительное давление подцилиндрической поверхностью радиуса R согласно формуле (144.4) равно
вторым — окружность радиуса R*(R2=R). Кривизна цилиндрической поверхности по формуле (144.2) равна 1/2R, т. е. в 2 раза меньше, чем кривизна сферической поверхности того же радиуса. Дополнительное давление подцилиндрической поверхностью радиуса R согласно формуле (144.4) равно
 . Найдем радиус пузырька в воде, при котором добавочное давление равно 1 aт. Коэффициент поверхностного натяжения воды при 20°С равен 0,073 н/м, 1 ат соответствует примерно 105 н/м2. Следовательно, для R получается следующее значение:
. Найдем радиус пузырька в воде, при котором добавочное давление равно 1 aт. Коэффициент поверхностного натяжения воды при 20°С равен 0,073 н/м, 1 ат соответствует примерно 105 н/м2. Следовательно, для R получается следующее значение:



