Для тестовых примеров, имеющих аналитическое решение можно найти разность между приближенным и точным результатом. Распространение этой оценки на другие примеры очень ненадежно. Выход может быть найден, если вместо точного использовать приближенное, но более точное по сравнению с проверяемым значение. Однако при этом возникают два вопроса: как получить это более точное значение и как проверить, что оно действительно точнее исходного.
Более точное значение можно вычислить, пользуясь тем же способом, что и проверяемое. Но это приводит к дополнительным требованиям к ресурсам, которые могут оказаться невыполнимыми. Есть и другой способ: использовать более грубые результаты (с меньшим числом узлов и временем счета). Если погрешность метода подчиняется некоторому закону, то, зная этот закон (в виде характера зависимости, например, степенной, экспоненциальный и т.п.), можно по нескольким результатам провести идентификацию и приближенно предсказать значение, соответствующее бесконечному числу узлов.
Ответить на второй вопрос можно с помощью повторной экстраполяции, т.е. экстраполяцией экстраполированных результатов, полученных для разных наборов исходных данных. В этом случае получается оценка погрешности экстраполированных результатов (или размытость оценки погрешности). Если эта оценка удовлетворяет требованиям: в три и более раз меньше оценки погрешности исходных данных (относительная размытость меньше 1/3 [9]), то цель достигнута. Если нет, то данный способ оценки в конкретном случае следует признать ненадежным. Подробнее о критерии надежности сказано ниже.
Кроме того, при хороших оценках результаты экстраполяции можно использовать вместо вычисленных данных, как более точные. При этом необходима дополнительная экстраполяция, чтобы убедиться в надежности полученных таким способом результатов. В некоторых случаях путем повторной экстраполяции можно получить результаты, на многие порядки более точные, чем рассчитанные непосредственно с помощью численного метода, и чего невозможно было бы добиться прямым расчетом в связи с огромными затратами времени, превышающими разумные пределы.
Численная фильтрация
При экстраполяции требуется априорное знание характера зависимости результата расчетов от числа узлов (или математической модели погрешности), например
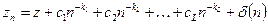 , (6)
, (6)
где 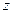 – точное значение;
– точное значение; 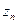 – приближенный результат, полученный при числе узловых точек, равном n;
– приближенный результат, полученный при числе узловых точек, равном n; 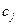 – коэффициенты, которые предполагаются не зависящими от n;
– коэффициенты, которые предполагаются не зависящими от n; 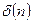 – величина, полагаемая малой по сравнению с
– величина, полагаемая малой по сравнению с 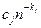 при тех значениях n, которые использовались в данных конкретных расчетах, k 1,…, kL – произвольные действительные числа (предполагается, что k 1< k 2<…< < kL).
при тех значениях n, которые использовались в данных конкретных расчетах, k 1,…, kL – произвольные действительные числа (предполагается, что k 1< k 2<…< < kL).
В математическом анализе обычно оценивается только первый член, поскольку остальные являются асимптотически (при n ®¥) бесконечно малыми более высокого порядка. Однако для конечных n остальные слагаемые могут вносить существенный вклад и должны приниматься во внимание.
Если решение задачи представляет собой функцию с несколькими непрерывными производными, то можно допустить возможность его разложения по формуле Тейлора, тогда 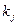 – это часть ряда натуральных чисел. Тогда к задаче нахождения предельного при
– это часть ряда натуральных чисел. Тогда к задаче нахождения предельного при 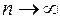 значения z можно подойти как к задаче интерполяции зависимости
значения z можно подойти как к задаче интерполяции зависимости 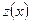 от параметра
от параметра 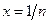 алгебраическим многочленом с последующей экстраполяцией до
алгебраическим многочленом с последующей экстраполяцией до 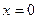 . Есть и другой подход, приводящий при условии постоянства
. Есть и другой подход, приводящий при условии постоянства 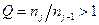 к тому же алгоритму, но не требующий целочисленности
к тому же алгоритму, но не требующий целочисленности 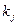 . Это решение задачи численной фильтрации, т.е. последовательное устранение степенных слагаемых суммы (6) при сохранении значения константы z. Рассмотрим два значения
. Это решение задачи численной фильтрации, т.е. последовательное устранение степенных слагаемых суммы (6) при сохранении значения константы z. Рассмотрим два значения 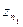 ,
, 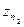 , вычисленные при числе узлов, равном
, вычисленные при числе узлов, равном 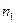 и
и 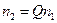 соответственно. Составим линейную комбинацию
соответственно. Составим линейную комбинацию
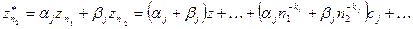
и потребуем, чтобы, суммарный коэффициент при z был равен 1, а при 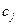 (для определенного j) равен 0. Отсюда получим формулу фильтрации, которая совпадает с экстраполяционной формулой Ричардсона [1]
(для определенного j) равен 0. Отсюда получим формулу фильтрации, которая совпадает с экстраполяционной формулой Ричардсона [1]
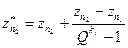 . (7)
. (7)
Проводя последовательно экстраполяцию по всем парам соседних значений, получим отфильтрованную зависимость, не содержащую члена с 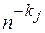
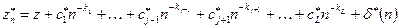 , (8)
, (8)
где 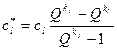 . (9)
. (9)
Заметим, что отфильтрованная последовательность 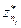 содержит на один член меньше, чем исходная. Если она содержит больше одного члена, то ее также можно отфильтровать, устранив степенную составляющую с
содержит на один член меньше, чем исходная. Если она содержит больше одного члена, то ее также можно отфильтровать, устранив степенную составляющую с 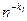 . Операции фильтрации можно повторять последовательно для
. Операции фильтрации можно повторять последовательно для 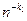 ,…,
,…, 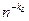 , если исходная последовательность содержит достаточное количество членов. Результаты экстраполяций удобно представлять в виде треугольной матрицы
, если исходная последовательность содержит достаточное количество членов. Результаты экстраполяций удобно представлять в виде треугольной матрицы
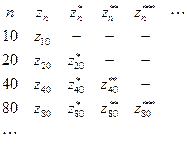 (10)
(10)
Применение повторной экстраполяции при kj = j известно под названием метода Ромберга. При его применении возникает ряд ограничений.
Применение повторной экстраполяции приводит к изменению коэффициентов суммы (6). При 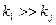 увеличение абсолютной величины коэффициентов может оказаться весьма существенным. Это ограничивает число возможных экстраполяций.
увеличение абсолютной величины коэффициентов может оказаться весьма существенным. Это ограничивает число возможных экстраполяций.
Величина 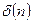 в (6) может оказаться суммой регулярной составляющей, имеющей вид
в (6) может оказаться суммой регулярной составляющей, имеющей вид  , и нерегулярной составляющей
, и нерегулярной составляющей 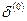 , обусловленной погрешностью исходных данных, которая, например, связана с ограниченной разрядностью чисел в машинном представлении. Тогда исходная нерегулярная часть погрешности, содержащаяся в вычисленных значениях
, обусловленной погрешностью исходных данных, которая, например, связана с ограниченной разрядностью чисел в машинном представлении. Тогда исходная нерегулярная часть погрешности, содержащаяся в вычисленных значениях 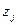 , при каждой экстраполяции умножается на коэффициент
, при каждой экстраполяции умножается на коэффициент
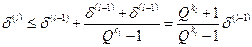 .
.
Для метода Ромберга, применяемого к последовательности (6) при 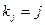 , произведение таких множителей ограничено числом, приблизительно равным 8 (получено численно), т.е. метод Ромберга является устойчивым к погрешности исходных данных, но сам уровень нерегулярной погрешности может ограничить число возможных экстраполяций.
, произведение таких множителей ограничено числом, приблизительно равным 8 (получено численно), т.е. метод Ромберга является устойчивым к погрешности исходных данных, но сам уровень нерегулярной погрешности может ограничить число возможных экстраполяций.
Процесс Эйткена
При оценке погрешности частичных сумм значение k в (2.4) может быть неизвестно. В этом случае можно использовать следующую модификацию правила Ричардсона. Вычислим три значения z 1, z 2, z 3 при трех номерах последовательности: n, nQ, nQ 2 и составим систему трех уравнений [1, 9]
 (11)
(11)
Найдем разности
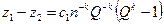 ,
,
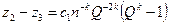 ,
,
и, разделив одну на другую, определим Qk
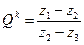 . (12)
. (12)
Теперь можно найти z
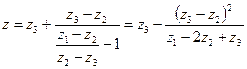 . (13)
. (13)
Как и в рассмотренных ранее случаях, мы нашли экстраполированное (уточненное) значение z = z *, а вместе с ним и оценку погрешности zi - z *.
Этот способ экстраполяции при неизвестном порядке точности принято называть алгоритмом Эйткена или d2-алгоритмом, который в более общем случае применяется для экстраполяции векторных последовательностей
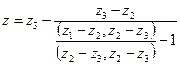 .
.
В последнем выражении zi – векторы, а скобками обозначается скалярное произведение.
Критерий размытости оценки
Оценка погрешности по правилу Рунге сводится к сравнению значения zn с экстраполированным значением 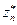 . Поскольку эта оценка справедлива при допущении, что величина
. Поскольку эта оценка справедлива при допущении, что величина 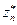 точнее, чем zn, то необходима проверка справедливости этого допущения. Это можно сделать следующим образом. Повторим процесс экстраполяции и получим значение
точнее, чем zn, то необходима проверка справедливости этого допущения. Это можно сделать следующим образом. Повторим процесс экстраполяции и получим значение 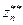 . Разность
. Разность 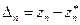 представляет собой оценку погрешности приближенного значения zn.. Разность
представляет собой оценку погрешности приближенного значения zn.. Разность 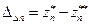 является оценкой погрешности экстраполированного значения
является оценкой погрешности экстраполированного значения 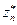 или оценкой погрешности оценки погрешности (рис. 10). Отношение
или оценкой погрешности оценки погрешности (рис. 10). Отношение 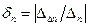 имеет смысл относительной размытости оценки погрешности.
имеет смысл относительной размытости оценки погрешности.
Если 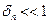 , то это означает, что относительная размытость оценки
, то это означает, что относительная размытость оценки 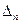 мала, и такой оценке можно доверять.
мала, и такой оценке можно доверять.
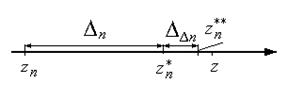
Рис. 10. Размытость оценки погрешности
Пусть оценка погрешности представляется в виде интервала 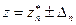 . Для определения порогового значения d n для принятия или отклонения полученной оценки желательно на основании имеющейся информации установить, не может ли при гипотетическом продолжении экстраполяций произойти переход получающихся значений левее
. Для определения порогового значения d n для принятия или отклонения полученной оценки желательно на основании имеющейся информации установить, не может ли при гипотетическом продолжении экстраполяций произойти переход получающихся значений левее 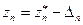 или правее
или правее 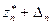 . Для этого предположим, что при последующих гипотетических экстраполяциях значение
. Для этого предположим, что при последующих гипотетических экстраполяциях значение 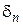 , как коэффициента уменьшения расстояния между соседними экстраполированными значениями, будет сохраняться:
, как коэффициента уменьшения расстояния между соседними экстраполированными значениями, будет сохраняться: 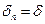 . Тогда предельное удаление предельного значения от
. Тогда предельное удаление предельного значения от 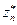 определяется суммой геометрической прогрессии
определяется суммой геометрической прогрессии 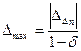 . Отсюда следует неравенство
. Отсюда следует неравенство
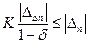 , (14)
, (14)
где K ³1 – коэффициент «запаса» надежности оценки. Необходимость введения коэффициента K вызвано желанием получать достаточно надежные оценки в условиях неопределенности, вызванной влиянием нерегулярных составляющих погрешности. Тогда получим условие (критерий принятия оценки)
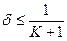 .
.
Примем величину K =2. Тогда пороговое значение 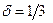 , тогда при
, тогда при 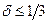 оценка принимается, а при
оценка принимается, а при 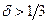 отвергается. Это же значение было получено эмпирически при анализе реальных численных данных [9].
отвергается. Это же значение было получено эмпирически при анализе реальных численных данных [9].



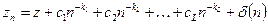 , (6)
, (6)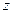 – точное значение;
– точное значение; 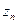 – приближенный результат, полученный при числе узловых точек, равном n;
– приближенный результат, полученный при числе узловых точек, равном n; 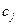 – коэффициенты, которые предполагаются не зависящими от n;
– коэффициенты, которые предполагаются не зависящими от n; 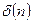 – величина, полагаемая малой по сравнению с
– величина, полагаемая малой по сравнению с 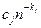 при тех значениях n, которые использовались в данных конкретных расчетах, k 1,…, kL – произвольные действительные числа (предполагается, что k 1< k 2<…< < kL).
при тех значениях n, которые использовались в данных конкретных расчетах, k 1,…, kL – произвольные действительные числа (предполагается, что k 1< k 2<…< < kL).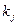 – это часть ряда натуральных чисел. Тогда к задаче нахождения предельного при
– это часть ряда натуральных чисел. Тогда к задаче нахождения предельного при 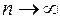 значения z можно подойти как к задаче интерполяции зависимости
значения z можно подойти как к задаче интерполяции зависимости 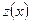 от параметра
от параметра 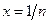 алгебраическим многочленом с последующей экстраполяцией до
алгебраическим многочленом с последующей экстраполяцией до 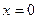 . Есть и другой подход, приводящий при условии постоянства
. Есть и другой подход, приводящий при условии постоянства 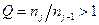 к тому же алгоритму, но не требующий целочисленности
к тому же алгоритму, но не требующий целочисленности 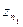 ,
, 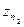 , вычисленные при числе узлов, равном
, вычисленные при числе узлов, равном 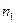 и
и 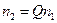 соответственно. Составим линейную комбинацию
соответственно. Составим линейную комбинацию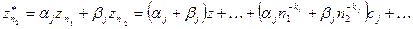
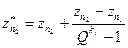 . (7)
. (7)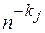
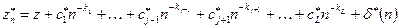 , (8)
, (8)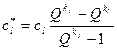 . (9)
. (9) содержит на один член меньше, чем исходная. Если она содержит больше одного члена, то ее также можно отфильтровать, устранив степенную составляющую с
содержит на один член меньше, чем исходная. Если она содержит больше одного члена, то ее также можно отфильтровать, устранив степенную составляющую с  . Операции фильтрации можно повторять последовательно для
. Операции фильтрации можно повторять последовательно для 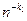 ,…,
,…, 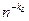 , если исходная последовательность содержит достаточное количество членов. Результаты экстраполяций удобно представлять в виде треугольной матрицы
, если исходная последовательность содержит достаточное количество членов. Результаты экстраполяций удобно представлять в виде треугольной матрицы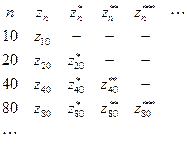 (10)
(10)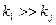 увеличение абсолютной величины коэффициентов может оказаться весьма существенным. Это ограничивает число возможных экстраполяций.
увеличение абсолютной величины коэффициентов может оказаться весьма существенным. Это ограничивает число возможных экстраполяций. , и нерегулярной составляющей
, и нерегулярной составляющей 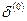 , обусловленной погрешностью исходных данных, которая, например, связана с ограниченной разрядностью чисел в машинном представлении. Тогда исходная нерегулярная часть погрешности, содержащаяся в вычисленных значениях
, обусловленной погрешностью исходных данных, которая, например, связана с ограниченной разрядностью чисел в машинном представлении. Тогда исходная нерегулярная часть погрешности, содержащаяся в вычисленных значениях 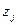 , при каждой экстраполяции умножается на коэффициент
, при каждой экстраполяции умножается на коэффициент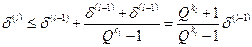 .
.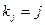 , произведение таких множителей ограничено числом, приблизительно равным 8 (получено численно), т.е. метод Ромберга является устойчивым к погрешности исходных данных, но сам уровень нерегулярной погрешности может ограничить число возможных экстраполяций.
, произведение таких множителей ограничено числом, приблизительно равным 8 (получено численно), т.е. метод Ромберга является устойчивым к погрешности исходных данных, но сам уровень нерегулярной погрешности может ограничить число возможных экстраполяций. (11)
(11)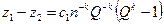 ,
,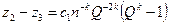 ,
,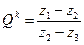 . (12)
. (12)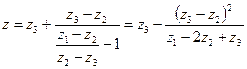 . (13)
. (13)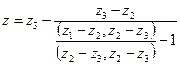 .
.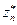 . Поскольку эта оценка справедлива при допущении, что величина
. Поскольку эта оценка справедлива при допущении, что величина 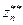 . Разность
. Разность 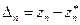 представляет собой оценку погрешности приближенного значения zn.. Разность
представляет собой оценку погрешности приближенного значения zn.. Разность 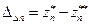 является оценкой погрешности экстраполированного значения
является оценкой погрешности экстраполированного значения 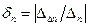 имеет смысл относительной размытости оценки погрешности.
имеет смысл относительной размытости оценки погрешности.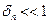 , то это означает, что относительная размытость оценки
, то это означает, что относительная размытость оценки 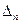 мала, и такой оценке можно доверять.
мала, и такой оценке можно доверять.
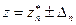 . Для определения порогового значения d n для принятия или отклонения полученной оценки желательно на основании имеющейся информации установить, не может ли при гипотетическом продолжении экстраполяций произойти переход получающихся значений левее
. Для определения порогового значения d n для принятия или отклонения полученной оценки желательно на основании имеющейся информации установить, не может ли при гипотетическом продолжении экстраполяций произойти переход получающихся значений левее 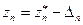 или правее
или правее 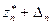 . Для этого предположим, что при последующих гипотетических экстраполяциях значение
. Для этого предположим, что при последующих гипотетических экстраполяциях значение 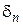 , как коэффициента уменьшения расстояния между соседними экстраполированными значениями, будет сохраняться:
, как коэффициента уменьшения расстояния между соседними экстраполированными значениями, будет сохраняться: 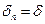 . Тогда предельное удаление предельного значения от
. Тогда предельное удаление предельного значения от 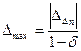 . Отсюда следует неравенство
. Отсюда следует неравенство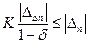 , (14)
, (14)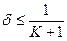 .
.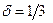 , тогда при
, тогда при 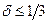 оценка принимается, а при
оценка принимается, а при 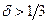 отвергается. Это же значение было получено эмпирически при анализе реальных численных данных [9].
отвергается. Это же значение было получено эмпирически при анализе реальных численных данных [9].


