

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Предложение, которое содержит хотя бы одну переменную и становится высказыванием при подстановке вместо всех переменных их значений, называется высказывательной формой.
Из высказывательных форм можно получать высказывания также с помощью специальных слов, так называемых кванторов. Их два: 1) квантор всеобщности – 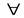 (любой, всякий, каждый); 2) квантор существования –
(любой, всякий, каждый); 2) квантор существования – 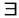 (существует, найдется, имеется, некоторый, по меньшей мере, один). Например, из высказывательной формы «Площадь комнаты 20 м2» можно с помощью кванторов получить высказывания: «Площадь любой комнаты 20 м2» – ложное, «Существует комната, площадь которой 20 м2» – истинное. Предложения, образованные с помощью квантора всеобщности, называются общеутвердительными; предложения, образованные с помощью квантора существования, называются частноутвердительными.
(существует, найдется, имеется, некоторый, по меньшей мере, один). Например, из высказывательной формы «Площадь комнаты 20 м2» можно с помощью кванторов получить высказывания: «Площадь любой комнаты 20 м2» – ложное, «Существует комната, площадь которой 20 м2» – истинное. Предложения, образованные с помощью квантора всеобщности, называются общеутвердительными; предложения, образованные с помощью квантора существования, называются частноутвердительными.
Союзы «и», «или», «если, то», «тогда и только тогда, когда», а также частицу «не» (словосочетание «неверно, что») называют логическими связками.
Предложения, образованные из других предложений с помощью логических связок, называют составными или сложными. Предложения, которые не содержат логических связок, называют элементарными или простыми.
1. Отрицание – единственная операция, которая может применяться к одному высказыванию.
Отрицанием высказывания называется новое высказывание, которое истинно тогда и только тогда, когда само высказывание ложно и ложно, когда само высказывание истинно.
Отрицание обозначается  , или b, читается: «не А» или «неверно, что А».
, или b, читается: «не А» или «неверно, что А».
Для произвольного высказывания А определение удобно записывать с помощью так называемой таблицы истинности:
| А | 
|
2.Конъюнкция (логическое умножение).
|
|
Конъюнкцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания истинны.
Конъюнкция обозначается 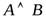 или А&B; читается: «А и В».
или А&B; читается: «А и В».
Таблица истинности для конъюнкции выглядит следующим образом:
| А | В | 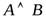
|
3. Дизъюнкция (логическое сложение).
Дизъюнкцией двух высказываний является новое высказывание, которое ложно тогда и только тогда, когда оба высказывания ложны.
Дизъюнкция обозначается 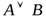 и читается «А или В».
и читается «А или В».
Таблица истинности для дизъюнкции выглядит следующим образом:
| А | В | 
|
4. Импликация (логическое следствие).
Эквиваленцией двух высказываний называется новое высказывание, которое истинно тогда и только тогда, когда оба высказывания одновременно истинны либо ложны.
Эквиваленция обозначается  или
или 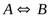 , читается «А тогда и только тогда, когда В».
, читается «А тогда и только тогда, когда В».
Таблица истинности для эквиваленции выглядит так:
| А | В | 
|
В форме эквиваленции, как правило, формулируются определения (например, определения логических операций).
3. Дать определения функции, композиции функций и указать их свойства.
Определение.
Пусть даны две переменные х и y с областями изменения Х и Y. Переменная y называется функцией от х, если по некоторому правилу или закону каждому значению  ставится в соответствие одно определенное значение
ставится в соответствие одно определенное значение  .
.
Для указания этого факта, что y есть функция от х, пишут:  ,
, 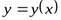 ,
,  и т.п.
и т.п.
Можно также сказать, что функция f отображает множество Х на множество Y. Это обозначается так 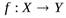 (рис.1.1).
(рис.1.1).
 Рис. 1.1
Рис. 1.1
Переменная х называется независимой переменной или аргументом.
Переменная y называется зависимой переменной или функцией.
Относительно самих величин х и y говорят, что они находятся в функциональной зависимости.
Область определения и изменения функции
|
|
Определение.
Совокупность всех значений независимой переменной х, для которых функция y определена, называется областью определения или областью существования этой функции.
Определение.
Множество Х называется областью определения функции и обозначается 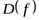 .
.
Определение.
Множество значений Y называется областью изменения или областью значений функции, и обозначается  .
.
Область изменения функции (множество ее значений) определяется законом соответствия.
Определение.
Функция 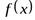 называется числовой функцией, если ее область определения
называется числовой функцией, если ее область определения 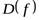 и множество значений
и множество значений  содержатся в множестве действительных чисел R.
содержатся в множестве действительных чисел R.
В дальнейшем будем изучать лишь числовые функции. Частное значение функции 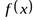 при
при  записывается так:
записывается так: 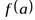 .
.
Характеризуют функцию по следующим свойствам:
Рассмотрим эти характеристики.
Четные и нечетные функции
Определение.
Функция  называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е.
называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е.  .
.
График четной функции расположен симметрично относительно оси  .
.
Определение.
Функция  называется нечетной, если при изменении знака аргумента знак функции меняется на противоположный, а числовое значение её сохраняется, т.е.
называется нечетной, если при изменении знака аргумента знак функции меняется на противоположный, а числовое значение её сохраняется, т.е. 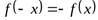 .
.
График нечетной функции расположен симметрично относительно начала координат.
Функция может быть ни четной ни нечетной, и в этом случае её называют функцией общего вида.
Графики таких функций не симметричны ни относительно оси  , ни относительно начала координат.
, ни относительно начала координат.
Периодические функции
Определение.
Функция  называется периодической, если существует такое положительное число
называется периодической, если существует такое положительное число  , что
, что  в области определения функции.
в области определения функции.
Наименьшее из положительных чисел Т, удовлетворяющих условию определения, называется периодом функции 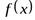 .
.
Нули функции
Определение.
Значение аргумента, при котором функция обращается в нуль,  , называется нулем функции.
, называется нулем функции.
Монотонные функции
Определение.
Функция называется возрастающей (убывающей) в некоторой области изменения аргумента, если большему значению аргумента соответствует большее (меньшее) значение функции.
|
|
Определение.
Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной.
Ограниченные функции
Определение.
Функция  называется ограниченной на множестве Х, если существует такое число
называется ограниченной на множестве Х, если существует такое число  , что для всех
, что для всех  выполняется неравенство
выполняется неравенство  .
.
Например, функции 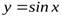 и
и 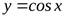 – ограниченные функции, т.к.
– ограниченные функции, т.к. 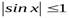 и
и 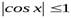 для
для  .
.
График ограниченной функции лежит между прямыми  и
и 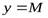 .
.
Пусть даны числовые функции f(x) и g(x), такие, что E(f) ⊂ UD(g). Их композицией называется новая числовая функция F, заданная на D(f), которая каждому x ∈ D(f) ставит в соответствие число g[f(x)]. Функцию F обозначают также: g○ f:
(g ○ f) (x) = g(f(x))
Если функции f(x) и g(x) заданы своими выражениями, то для получения выражения композиции этих функций надо подставить в выражение функции g(x) вместо x выражение функции f(x).
Свойства композиции
Композиция ассоциативна:
 .
.
Если  — тождественное отображение на
— тождественное отображение на  , то есть
, то есть
 ,
,
то
 .
.
Если  — тождественное отображение на
— тождественное отображение на  , то есть
, то есть
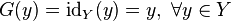 ,
,
то
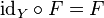 .
.
Рассмотрим пространство всех биекций множества  на себя и обозначим его
на себя и обозначим его  . То есть если
. То есть если 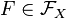 , то
, то  — биекция. Тогда композиция функций из
— биекция. Тогда композиция функций из  является бинарной операцией, а
является бинарной операцией, а  — группой.
— группой. 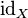 является нейтральным элементом этой группы. Обратным к элементу
является нейтральным элементом этой группы. Обратным к элементу 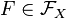 является
является 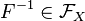 — обратная функция.
— обратная функция.
Группа  , вообще говоря, не коммутативна, то есть
, вообще говоря, не коммутативна, то есть  .
.
Свойства отношений
Определение 1. Бинарное отношение на множестве X называется рефлексивным, если для любого элемента a 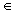 X выполняется условие a a:
X выполняется условие a a:
(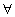 a
a 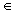 X) a a.
X) a a.
Определение 2. Бинарное отношение на X называется антирефлексивным, если ни для одного a 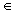 X не выполняется условие a a:
X не выполняется условие a a:
(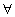 a
a 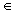 X)
X) 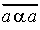 .
.
Определение 3. Бинарное отношение на множестве X называется симметричным, если из a b следует b a:
(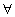 a, b
a, b 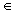 X)(a b
X)(a b 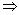 b a).
b a).
Определение 4. Бинарное отношение на множестве X называется антисимметричным, если для любых различных элементов a и b условия a b и b a не выполняются одновременно:
(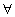 a, b
a, b 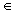 X) (a b & b a
X) (a b & b a 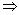 a = b).
a = b).
Определение 5. Бинарное отношение a на множестве X называется транзитивным, если для любых трех элементов a, b, c 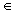 X из a b и b c следует a c:
X из a b и b c следует a c:
|
|
(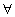 a, b, c
a, b, c 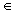 X) (a b & b c a c).
X) (a b & b c a c).
Определение 6. Бинарное отношение на множестве X называется связным, если для любых двух различных элементов a и b имеет место a b, либо b a:
(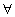 a, b, c
a, b, c 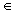 X)(a
X)(a 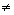 b
b 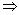 a b
a b 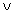 b a).
b a).
Определение 1
Пусть имеем систему из n-векторов  и имеем набор чисел
и имеем набор чисел  , тогда
, тогда
 (1)
(1)
называется линейной комбинацией данной системы векторов с данным набором коэффициентов.
Определение 2 (через нулевую линейную комбинацию)
Система векторов  называется линейно зависимой, если существует такой набор коэффициентов
называется линейно зависимой, если существует такой набор коэффициентов  , из которых хотя бы один не равен нулю, что линейная комбинация данной системы векторов с этим набором коэффициентов равна нулевому вектору:
, из которых хотя бы один не равен нулю, что линейная комбинация данной системы векторов с этим набором коэффициентов равна нулевому вектору:
 . (2)
. (2)
Пусть  , тогда
, тогда

Определение 3 ( через представление одного вектора системы в виде линейной комбинации остальных)
Система векторов  называется линейно зависимой, если хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов этой системы.
называется линейно зависимой, если хотя бы один из векторов этой системы можно представить в виде линейной комбинации остальных векторов этой системы.
Утверждение 1
Определения 2 и 3 эквивалентны.
Теорема Кронекера-Капелли.
Для того, чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы.
Доказательство теоремы.
Необходимость. Система 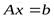 совместна. Докажем, что
совместна. Докажем, что 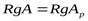 .
.
Система 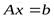 совместна — существуют такие числа
совместна — существуют такие числа 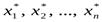 ,что
,что

т.е. вектор-столбец правой части линейно выражается через столбцы 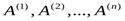 матрицы A. Это означает, что при добавлении столбца
матрицы A. Это означает, что при добавлении столбца 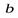 число линейно независимых столбцов не увеличивается, т.е.
число линейно независимых столбцов не увеличивается, т.е. 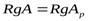 . Необходимость доказана.
. Необходимость доказана.
Достаточность. 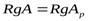 . Докажем, что система
. Докажем, что система 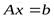 совместна.
совместна.
Пусть 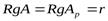 . Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов
. Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов  . Тогда столбцы
. Тогда столбцы 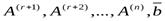 — линейно зависимы и, следовательно, столбец
— линейно зависимы и, следовательно, столбец 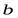 линейно выражается через
линейно выражается через 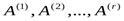 :
:  .
.
Положим 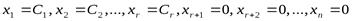 ,
,
тогда
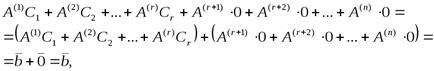
т.е. вектор 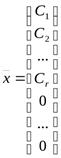 — решение системы
— решение системы  ,
,
т.е. система  совместна. Теорема доказана.
совместна. Теорема доказана.
Предложение, которое содержит хотя бы одну переменную и становится высказыванием при подстановке вместо всех переменных их значений, называется высказывательной формой.
Из высказывательных форм можно получать высказывания также с помощью специальных слов, так называемых кванторов. Их два: 1) квантор всеобщности – 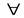 (любой, всякий, каждый); 2) квантор существования –
(любой, всякий, каждый); 2) квантор существования – 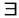 (существует, найдется, имеется, некоторый, по меньшей мере, один). Например, из высказывательной формы «Площадь комнаты 20 м2» можно с помощью кванторов получить высказывания: «Площадь любой комнаты 20 м2» – ложное, «Существует комната, площадь которой 20 м2» – истинное. Предложения, образованные с помощью квантора всеобщности, называются общеутвердительными; предложения, образованные с помощью квантора существования, называются частноутвердительными.
(существует, найдется, имеется, некоторый, по меньшей мере, один). Например, из высказывательной формы «Площадь комнаты 20 м2» можно с помощью кванторов получить высказывания: «Площадь любой комнаты 20 м2» – ложное, «Существует комната, площадь которой 20 м2» – истинное. Предложения, образованные с помощью квантора всеобщности, называются общеутвердительными; предложения, образованные с помощью квантора существования, называются частноутвердительными.
|
|
|
|
|

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!