ВВЕДЕНИЕ
Первое, дошедшее до нас, научное изложение геометрии содержится в труде «Начала», составленном древнегреческим ученым Евклидом, жившим в III веке до нашей эры в городе Александрии. Именно Евклидом была сделана первая попытка дать аксиоматическое изложение геометрии. Впервые научная система аксиом Евклида была сформулирована Д. Гильбертом (1862-1943) в конце CIC века.
Школьный курс геометрии состоит из двух частей: планиметрии и стереометрии. В планиметрии изучаются свойства геометрических фигур на плоскости.
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «стереос» – объемный, пространственный и «метрео» – измерять.
Представление о геометрических телах, изучаемых в стереометрии, дают окружающие нас предметы. В отличие от реальных предметов геометрические тела являются воображаемыми объектами. Изучая свойства геометрических тел, мы получаем представление о геометрических свойствах реальных предметов и можем использовать эти свойства в практической деятельности. Геометрия, в частности стереометрия, широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники.
Схема построения геометрии
Перечисляются основные неопределяемые понятия.
Формулируются свойства основных понятий - аксиомы.
Определяются другие геометрические понятия.
Формулируются и доказываются свойства геометрических понятий - теоремы.
АКСИОМЫ СТЕРЕОМЕТРИИ. СЛЕДСТВИЯ ИЗ АКСИОМ
Основные понятия стереометрии: точка, прямая, плоскость, расстояние.
Определение: Аксиомой называется предложение, не требующее доказательства .
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах. Вся система аксиом стереометрии состоит из ряда аксиом, известных нам по курсу планиметрии, и аксиом о взаимном расположении точек, прямых и плоскостей в пространстве.
АКСИОМЫ СТЕРЕОМЕТРИИ
I. Аксиомы принадлежности
 I1. Существуют хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек.
I1. Существуют хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек.
Обозначение:
А, В, С, D – точки;
а, b, с – прямые;
a, b, g – плоскости;
А Î а – точка А принадлежит прямой а, прямая а проходит через точку А;
Е Ï а – точка Е не принадлежит прямой а;
С Î a – точка С принадлежит плоскости a, плоскость a проходит через точку С;
Е Ï a – точка Е не принадлежит плоскости a.
Вывод: Существуют точки, принадлежащие прямой и не принадлежащие прямой, существуют точки, принадлежащие плоскости и не принадлежащие плоскости.
I2. Через две различные точки проходит одна и только одна прямая.
Обозначение: а = АВ
Вывод: Прямые, имеющие две различные общие точки, совпадают.
I3. Прямая, проходящая через две любые точки плоскости, лежит в этой плоскости.
Обозначение:
а Ì a – плоскость a проходит через прямую а;
b Ë a – плоскость a не проходит через прямую b.
 I4. Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость.
I4. Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость.
Обозначение: a = АВС
 Вывод: Плоскости, имеющие три различные общие точки, совпадают.
Вывод: Плоскости, имеющие три различные общие точки, совпадают.
I5. Если две различные плоскости имеют общую точку, то их пересечением является прямая.
Обозначение: М Î a, М Î b, a ¹ b, a ìü b = l.
II. Аксиомы расстояния
II1. Для любых двух точек А и В имеется неотрицательная величина, называемая расстоянием от А до В. Расстояние АВ равно нулю тогда и только тогда, когда точки А и В совпадают.
Обозначение: АВ ³ 0.
II2. Расстояние от А до В равно расстоянию от В до А.
Обозначение: АВ = ВА.
 II3. Для любых трех точек А, В, С расстояние от А до С не больше суммы расстояний от А до В и от В до С.
II3. Для любых трех точек А, В, С расстояние от А до С не больше суммы расстояний от А до В и от В до С.
Обозначение: АС £ АВ + ВС.
III. Аксиомы порядка
III1. Любая точка О прямой р разбивает множество всех отличных от точки О точек прямой р на два непустых множества так, что для любых двух точек А и В, принадлежащим разным множествам, точка О лежит между точками А и В; если точки А и В принадлежат одному и тому же множеству, то одна из них лежит между другой и точкой О.
III2. Для любого расстояния а на заданном луче с началом О существует одна и только одна точка А, расстояние от которой до точки О равно а.
 III3. Если точка С лежит между точками А и В, то точки А, В, С принадлежат одной прямой.
III3. Если точка С лежит между точками А и В, то точки А, В, С принадлежат одной прямой.
 III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
IV. Аксиома подвижности плоскости
Если точки А, В, А1, В1 лежат в плоскости a, причем АВ > 0 и АВ = А1В1, то существует два и только два перемещения этой плоскости, каждое из которых отображает точку А на точку А1 а точку В на точку В1.
V. Аксиома параллельных
Через точку А проходит не более одной прямой, параллельной данной прямой р.
СЛЕДСТВИЯ ИЗ АКСИОМ
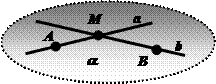
Следствие 1: Через прямую и не принадлежащую ей точку можно провести одну и только одну плоскость.
Дано: М, а, М Ï а
Доказать:
1.  ;
;
2.  .
.
Доказательство:
1. Выберем на прямой а точки А и В (аксиома I1 ): А Î а, В Î а.
Через точки М, А, В проходит плоскость a (аксиома I4 ): a = МАВ.
Так как точки А, В принадлежат плоскости a, то прямая а принадлежит плоскости a (аксиома I3 ): а Ì a.
Следовательно, существует плоскость a, проходящая через прямую а и не принадлежащую ей точку М:  .
.
2. Плоскость a содержит прямую а и точку М, то есть проходит через точки М, А, В. Через три точки, не принадлежащие одной прямой, проходит единственная плоскость (аксиома I4 ).
Следствие 2: Через две пересекающиеся прямые можно провести одну и только одну плоскость.
Дано: а, b, а ´ b
Доказать:
1.  ;
;
2.  .
.
Доказательство:
1. Обозначим точку пересечения прямых а и b:  .
.
Выберем на прямой а точку А, на прямой b точку В (аксиома I1 ): А Î а, В Î b.
Через точки М, А, В проходит плоскость a (аксиома I4 ): a = МАВ.
Так как точки А, М принадлежат плоскости a, то прямая а принадлежит плоскости a (аксиома I3 ): АМ = а Ì a.
Так как точки В, М принадлежат плоскости a, то прямая b принадлежит плоскости a (аксиома I3 ): ВМ = b Ì a.
Следовательно, существует плоскость a, проходящая через две пересекающиеся прямые а и b:  .
.
2. Плоскость a содержит прямые а и b, то есть проходит через точки М, А, В. Через три точки, не принадлежащие одной прямой, проходит единственная плоскость (аксиома I4 ).
 Определение: Прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек или совпадают.
Определение: Прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек или совпадают.

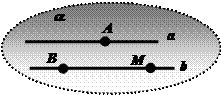 Следствие 3: Через две параллельные прямые можно провести одну и только одну плоскость.
Следствие 3: Через две параллельные прямые можно провести одну и только одну плоскость.
Дано: а, b, 
Доказать:
1.  ;
;
2.  .
.
Доказательство:
1. Существование плоскости a, проходящей через две параллельные прямые а и b, следует из определения параллельных прямых.
2. Предположим, что существует другая плоскость, содержащая прямые а и b. Выберем на прямой а точку А, на прямой b точки В и М (аксиома I1 ): А Î а, В Î b, М Î b. Получили, что через точки А, В, М проходят две плоскости, что противоречит аксиоме I4. Следовательно, предположение не верно, плоскость а – единственная.
Упражнения:
1. Прочитать запись и сделать схематический рисунок:
a)  ;
;
b)  ;
;
c) 
 ;
;
d)  .
.
2. По рисунку назвать:
a) плоскости, в которых лежат прямые РЕ, МК, DВ, АВ, ЕС;
b) точки пересечения прямой DК с плоскостью АВС, прямой СЕ с плоскостью АDВ;
c) точки, лежащие в плоскостях АDВ и DВС;
d)  прямые, по которым пересекаются плоскости АВС и DСВ, АВD и СDА, РDС и АВС.
прямые, по которым пересекаются плоскости АВС и DСВ, АВD и СDА, РDС и АВС.
3. По рисунку назвать:
a) точки, лежащие в плоскостях DСС1 и ВQС;
b) плоскости, в которых лежит прямая АА1;
c) точки пересечения прямой МК с плоскостью АВD, прямых DК и ВР с плоскостью А1В1С1;
d) прямые, по которым пересекаются плоскости АА1В1 и АСD, РВ1С1 и АВС;
e) точки пересечения прямых МК и DС, В1С1 и ВР, С1М и DС.
3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ В ПРОСТРАНСТВЕ
ПРИЗНАК СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ
Рис. 1. Рис. 2. Рис. 3.
Определение: Плоскости параллельны, если они не имеют общих точек или совпадают.
ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД
 В теме «Геометрические тела, их поверхности и объёмы» мы будем изучать многогранники – геометрические тела, поверхности которых составлены из многоугольников. Для иллюстрации понятий, связанных с взаимным расположением прямых и плоскостей в пространстве познакомимся с двумя многогранниками – тетраэдром и параллелепипедом.
В теме «Геометрические тела, их поверхности и объёмы» мы будем изучать многогранники – геометрические тела, поверхности которых составлены из многоугольников. Для иллюстрации понятий, связанных с взаимным расположением прямых и плоскостей в пространстве познакомимся с двумя многогранниками – тетраэдром и параллелепипедом.
Рассмотрим произвольный треугольник АВС и точку D, не лежащую в плоскости этого треугольника. Соединив точку D отрезками с вершинами треугольника АВС, получим треугольники DАВ, DВС, DСА.
Поверхность, составленная из четырёх треугольников АВС, DАВ, DВС, DСА, называется тетраэдром и обозначается DАВС.
Треугольники, из которых состоит тетраэдр, называются гранями, их стороны – рёбрами, а вершины – вершинами тетраэдра. Тетраэдр имеет четыре грани, шесть рёбер и четыре вершины.
Два ребра тетраэдра, не имеющие общих вершин, называются противоположными. У тетраэдра DАВС противоположными являются рёбра АD и ВС, ВD и АС, СD и АВ. Часто одну из граней тетраэдра называют основанием, и три другие – боковыми гранями.
 Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1, СС1 и DD1 параллельны. Четырёхугольники АВВ1А1, ВСС1В1, СDD1С1, DАА1D1 также являются параллелограммами, так как каждый из них имеет попарно параллельные противоположные стороны.
Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1, СС1 и DD1 параллельны. Четырёхугольники АВВ1А1, ВСС1В1, СDD1С1, DАА1D1 также являются параллелограммами, так как каждый из них имеет попарно параллельные противоположные стороны.
Поверхность, составленная из двух равных параллелограммов АВСD и А1В1С1D1 и четырёх параллелограммов АВВ1А1, ВСС1В1, СDD1С1, DА А1D1, называется параллелепипедом и обозначается АВСDА1В1С1D1.
Параллелограммы, из которых составлен параллелепипед, называются гранями, их стороны – рёбрами, а вершины параллелограммов – вершинами параллелепипеда. Параллелепипед имеет шесть граней, двенадцать рёбер и восемь вершин. Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер – противоположными. Две вершины, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Каждый параллелепипед имеет четыре диагонали.
Диагоналями параллелепипеда АВСDА1В1С1D1 являются отрезки АС1, ВD1, СА1, DВ1.
Часто выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани – боковыми гранями параллелепипеда. Рёбра параллелепипеда, не принадлежащие основаниям, называются боковыми рёбрами.
 Если в качестве оснований параллелепипеда АВСDА1В1С1D1 выбрать грани АВСD и А1В1С1D1, то боковыми гранями будут параллелограммы АВВ1А1, ВСС1В1, СDD1С1, DА А1D1, а боковыми рёбрами отрезки АА1, ВВ1, СС1 и DD1.
Если в качестве оснований параллелепипеда АВСDА1В1С1D1 выбрать грани АВСD и А1В1С1D1, то боковыми гранями будут параллелограммы АВВ1А1, ВСС1В1, СDD1С1, DА А1D1, а боковыми рёбрами отрезки АА1, ВВ1, СС1 и DD1.
Упражнения:
1. В тетраэдре DАВС точки М, N, Q, Р – середины отрезков ВD, DС, АС, АВ. Найти периметр четырехугольника МNQР, если АD = 12 см, ВС = 14 см.
УГОЛ МЕЖДУ ПРЯМЫМИ
 Определение: Углом между непараллельными прямыми т и п называется меньший из смежных углов, образованных пересекающимися прямыми т' и п', где т' || т, п' || п.
Определение: Углом между непараллельными прямыми т и п называется меньший из смежных углов, образованных пересекающимися прямыми т' и п', где т' || т, п' || п.
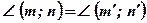 ,
,  ,
,  .
.
Замечание: Угол между параллельными прямыми считается равным нулю.
Определение: Две прямые в пространстве называются перпендикулярными, если угол между ними равен  .
.
Обозначение: 
Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
Задача: Дан куб АВСDА1В1С1D1.
Найти:  ;
;  ;
;  .
.
Решение:
По признаку параллельности двух прямых:
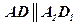 и
и  , следовательно,
, следовательно, 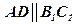 .
.  .
.
 .
.  , так как СDD1С1 является квадратом.
, так как СDD1С1 является квадратом.
 .
.
По признаку скрещивающихся прямых:
 , следовательно,
, следовательно,  ·
·  .
.
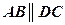 , следовательно,
, следовательно,  .
.
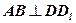 .
.
Вывод: 
Из центра О круга радиуса 3 дм восстановлен перпендикуляр ОВ к его плоскости. К окружности проведена касательная в точке А и на этой касательной отложен от точки касания отрезок АС, равный 2 дм. Найти длину наклонной ВС, если длина перпендикуляра ОВ равна 6 дм.
5. Из вершины D прямоугольника АВСD, стороны которого АВ = 9 см и ВС = 8 см, восстановлен к плоскости прямоугольника перпендикуляр DF = 12 см. Найти расстояния от точки F до вершин прямоугольника.
8. ДВУГРАННЫЙ УГОЛ. ЛИНЕЙНЫЙ УГОЛ ДВУГРАННОГО УГЛА
 III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
Множества, на которые прямая р разбивает множество не принадлежащих ей точек плоскости a, называются открытыми полуплоскостями с границей р.
Сторона ВС прямоугольника АВСD служит стороной треугольника ВСF, причём вершина F проектируется на DС. Назвать линейный угол двугранного угла, образованного плоскостями АВС и ВСF (Рис. 1.).
Рис. 1. Рис. 2.
Дано изображение равнобедренной трапеции АВСD и треугольника АВМ. Отрезок МС перпендикулярен плоскости АВС. Построить линейный угол двугранного угла, образованного плоскостями АВС и ВСМ так, чтобы одна из его сторон проходила через точку М (Рис. 2.).
3. На грани двугранного угла, равного 45°, дана точка, удалённая от ребра на 4 см. Найти расстояние от этой точки, до другой грани.
Многоугольник разбивается диагоналями, проведёнными из одной вершины, на конечное число треугольников, для каждого из которых теорема верна. Поэтому теорема будет верна и для суммы площадей всех треугольников, плоскости которых образуют один и тот же угол с плоскостью проекции.
Замечание: Доказанная теорема справедлива для любой плоской фигуры, ограниченной замкнутой кривой.

Упражнения:
1. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом  , если проекция его – правильный треугольник со стороной а.
, если проекция его – правильный треугольник со стороной а.
2. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом  , если проекция его – равнобедренный треугольник с боковой стороной 10 см и основанием 12 см.
, если проекция его – равнобедренный треугольник с боковой стороной 10 см и основанием 12 см.
3. Найти площадь треугольника, плоскость которого наклонена к плоскости проекции под углом  , если проекция его – треугольник со сторонами 9, 10 и 17 см.
, если проекция его – треугольник со сторонами 9, 10 и 17 см.
4. Вычислить площадь трапеции, плоскость которой наклонена к плоскости проекции под углом  , если проекция её – равнобедренная трапеция, большее основание которой 44 см, боковая сторона 17 см и диагональ 39 см.
, если проекция её – равнобедренная трапеция, большее основание которой 44 см, боковая сторона 17 см и диагональ 39 см.
5. Вычислить площадь проекции правильного шестиугольника со стороной 8 см, плоскость которого наклонена к плоскости проекции под углом  .
.
6. Ромб со стороной 12 см и острым углом  образует с данной плоскостью угол
образует с данной плоскостью угол  . Вычислить площадь проекции ромба на эту плоскость.
. Вычислить площадь проекции ромба на эту плоскость.
7. Ромб со стороной 20 см и диагональю 32 см образует с данной плоскостью угол  . Вычислить площадь проекции ромба на эту плоскость.
. Вычислить площадь проекции ромба на эту плоскость.
8. Проекция навеса на горизонтальную плоскость есть прямоугольник со сторонами  и
и  . Найти площадь навеса, если боковые грани – равные прямоугольники, наклонённые к горизонтальной плоскости под углом
. Найти площадь навеса, если боковые грани – равные прямоугольники, наклонённые к горизонтальной плоскости под углом  , а средняя часть навеса – квадрат, параллельный плоскости проекции.
, а средняя часть навеса – квадрат, параллельный плоскости проекции.
11. Упражнения по теме «Прямые и плоскости в пространстве»:
Стороны треугольника равны 20 см, 65 см, 75 см. Из вершины большего угла треугольника проведён к его плоскости перпендикуляр, равный 60 см. Найти расстояние от концов перпендикуляра до большей стороны треугольника.
2. Из точки, отстоящей от плоскости на расстоянии  см, проведены две наклонные, образующие с плоскостью углы, равные
см, проведены две наклонные, образующие с плоскостью углы, равные  , а между собой – прямой угол. Найти расстояние между точками пересечения наклонных с плоскостью.
, а между собой – прямой угол. Найти расстояние между точками пересечения наклонных с плоскостью.
3. Сторона правильного треугольника равна 12 см. Точка М выбрана так, что отрезки, соединяющие точку М со всеми вершинами треугольника, образуют с его плоскостью углы  . Найти расстояние от точки М до вершин и сторон треугольника.
. Найти расстояние от точки М до вершин и сторон треугольника.
4. Через сторону квадрата проведена плоскость под углом  к диагонали квадрата. Найти углы, под которыми наклонены к плоскости две стороны квадрата.
к диагонали квадрата. Найти углы, под которыми наклонены к плоскости две стороны квадрата.
5. Катет равнобедренного прямоугольного треугольника наклонён к плоскости a, проходящей через гипотенузу, под углом  . Доказать, что угол между плоскостью a и плоскостью треугольника равен
. Доказать, что угол между плоскостью a и плоскостью треугольника равен  .
.
6. Двугранный угол между плоскостями треугольников АВС и DВС равен  . Найти АD, если АВ = АС =5 см, ВС = 6 см, ВD = DС =
. Найти АD, если АВ = АС =5 см, ВС = 6 см, ВD = DС = 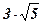 см.
см.
Контрольные вопросы по теме «Прямые и плоскости в пространстве»
1. Перечислить основные понятия стереометрии. Сформулировать аксиомы стереометрии.
2. Доказать следствия из аксиом.
3. Каково взаимное расположение двух прямых в пространстве? Дать определения пересекающихся, параллельных, скрещивающихся прямых.
4. Доказать признак скрещивающихся прямых.
5. Каково взаимное расположение прямой и плоскости? Дать определения пересекающихся, параллельных прямой и плоскости.
6. Доказать признак параллельности прямой и плоскости.
7. Каково взаимное расположение двух плоскостей?
8. Дать определение параллельных плоскостей. Доказать признак параллельности двух плоскостей. Сформулировать теоремы о параллельных плоскостях.
9. Дать определение угла между прямыми.
10. Доказать признак перпендикулярности прямой и плоскости.
11. Дать определения основания перпендикуляра, основания наклонной, проекции наклонной на плоскость. Сформулировать свойства перпендикуляра и наклонных, опущенных на плоскость из одной точки.
12. Дать определение угла между прямой и плоскостью.
13. Доказать теорему о трех перпендикулярах.
14. Дать определения двугранного угла, линейного угла двугранного угла.
15. Доказать признак перпендикулярности двух плоскостей.
16. Дать определение расстояния между двумя различными точками.
17. Дать определение расстояния от точки до прямой.
18. Дать определение расстояния от точки до плоскости.
19. Дать определение расстояния между прямой и параллельной ей плоскостью.
20. Дать определение расстояния между параллельными плоскостями.
21. Дать определение расстояния между скрещивающимися прямыми.
22. Дать определение ортогональной проекции точки на плоскость.
23. Дать определение ортогональной проекции фигуры на плоскость.
24. Сформулировать свойства проекций на плоскость.
25. Сформулировать и доказать теорему о площади проекции плоского многоугольника.
ВВЕДЕНИЕ
Первое, дошедшее до нас, научное изложение геометрии содержится в труде «Начала», составленном древнегреческим ученым Евклидом, жившим в III веке до нашей эры в городе Александрии. Именно Евклидом была сделана первая попытка дать аксиоматическое изложение геометрии. Впервые научная система аксиом Евклида была сформулирована Д. Гильбертом (1862-1943) в конце CIC века.
Школьный курс геометрии состоит из двух частей: планиметрии и стереометрии. В планиметрии изучаются свойства геометрических фигур на плоскости.
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «стереос» – объемный, пространственный и «метрео» – измерять.
Представление о геометрических телах, изучаемых в стереометрии, дают окружающие нас предметы. В отличие от реальных предметов геометрические тела являются воображаемыми объектами. Изучая свойства геометрических тел, мы получаем представление о геометрических свойствах реальных предметов и можем использовать эти свойства в практической деятельности. Геометрия, в частности стереометрия, широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники.
Схема построения геометрии



 I1. Существуют хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек.
I1. Существуют хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек.

 I4. Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость.
I4. Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость. Вывод: Плоскости, имеющие три различные общие точки, совпадают.
Вывод: Плоскости, имеющие три различные общие точки, совпадают.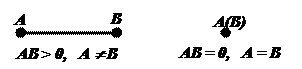
 II3. Для любых трех точек А, В, С расстояние от А до С не больше суммы расстояний от А до В и от В до С.
II3. Для любых трех точек А, В, С расстояние от А до С не больше суммы расстояний от А до В и от В до С.
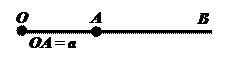
 III3. Если точка С лежит между точками А и В, то точки А, В, С принадлежат одной прямой.
III3. Если точка С лежит между точками А и В, то точки А, В, С принадлежат одной прямой. III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
 ;
; .
. .
.
 ;
; .
. .
. Определение: Прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек или совпадают.
Определение: Прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек или совпадают.
 Следствие 3: Через две параллельные прямые можно провести одну и только одну плоскость.
Следствие 3: Через две параллельные прямые можно провести одну и только одну плоскость.
 ;
; ;
;
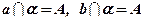 ;
;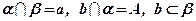 .
. прямые, по которым пересекаются плоскости АВС и DСВ, АВD и СDА, РDС и АВС.
прямые, по которым пересекаются плоскости АВС и DСВ, АВD и СDА, РDС и АВС. В теме «Геометрические тела, их поверхности и объёмы» мы будем изучать многогранники – геометрические тела, поверхности которых составлены из многоугольников. Для иллюстрации понятий, связанных с взаимным расположением прямых и плоскостей в пространстве познакомимся с двумя многогранниками – тетраэдром и параллелепипедом.
В теме «Геометрические тела, их поверхности и объёмы» мы будем изучать многогранники – геометрические тела, поверхности которых составлены из многоугольников. Для иллюстрации понятий, связанных с взаимным расположением прямых и плоскостей в пространстве познакомимся с двумя многогранниками – тетраэдром и параллелепипедом. Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1, СС1 и DD1 параллельны. Четырёхугольники АВВ1А1, ВСС1В1, СDD1С1, DАА1D1 также являются параллелограммами, так как каждый из них имеет попарно параллельные противоположные стороны.
Рассмотрим два равных параллелограмма АВСD и А1В1С1D1, расположенных в параллельных плоскостях так, что отрезки АА1, ВВ1, СС1 и DD1 параллельны. Четырёхугольники АВВ1А1, ВСС1В1, СDD1С1, DАА1D1 также являются параллелограммами, так как каждый из них имеет попарно параллельные противоположные стороны. Если в качестве оснований параллелепипеда АВСDА1В1С1D1 выбрать грани АВСD и А1В1С1D1, то боковыми гранями будут параллелограммы АВВ1А1, ВСС1В1, СDD1С1, DА А1D1, а боковыми рёбрами отрезки АА1, ВВ1, СС1 и DD1.
Если в качестве оснований параллелепипеда АВСDА1В1С1D1 выбрать грани АВСD и А1В1С1D1, то боковыми гранями будут параллелограммы АВВ1А1, ВСС1В1, СDD1С1, DА А1D1, а боковыми рёбрами отрезки АА1, ВВ1, СС1 и DD1. Определение: Углом между непараллельными прямыми т и п называется меньший из смежных углов, образованных пересекающимися прямыми т' и п', где т' || т, п' || п.
Определение: Углом между непараллельными прямыми т и п называется меньший из смежных углов, образованных пересекающимися прямыми т' и п', где т' || т, п' || п.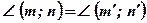 ,
,  ,
,  .
. .
.
 ;
;  ;
;  .
.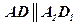 и
и  , следовательно,
, следовательно, 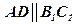 .
.  .
. .
.  , так как СDD1С1 является квадратом.
, так как СDD1С1 является квадратом. .
. , следовательно,
, следовательно,  ·
·  .
.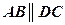 , следовательно,
, следовательно,  .
.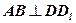 .
.
 III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.
III4. Любая прямая р, лежащая в плоскости a, разбивает множество не принадлежащих ей точек этой плоскости на два непустых множества так, что любые две точки, принадлежащие разным множествам, разделены прямой р; любые две точки, принадлежащие одному и тому же множеству, не разделены прямой р.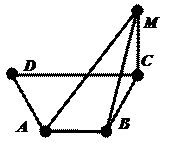


 , если проекция его – правильный треугольник со стороной а.
, если проекция его – правильный треугольник со стороной а. , если проекция её – равнобедренная трапеция, большее основание которой 44 см, боковая сторона 17 см и диагональ 39 см.
, если проекция её – равнобедренная трапеция, большее основание которой 44 см, боковая сторона 17 см и диагональ 39 см. .
. и
и  . Найти площадь навеса, если боковые грани – равные прямоугольники, наклонённые к горизонтальной плоскости под углом
. Найти площадь навеса, если боковые грани – равные прямоугольники, наклонённые к горизонтальной плоскости под углом  см, проведены две наклонные, образующие с плоскостью углы, равные
см, проведены две наклонные, образующие с плоскостью углы, равные 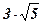 см.
см.

