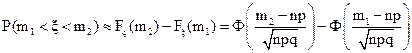Центральная предельная теорема

При изучении нормального распределения было сформулировано следующее утверждение: если случайные величины x₁, x₂, …, x _n независимы и нормальны с одними и теми же (а, s), то сумма x₁ + x₂ + … + x _n также нормальна. Оказывается справедливо гораздо более глубокое утверждение: если случайные величины независимы и имеют один и тот же закон распределения (неважно какой), то при достаточно большом числе слагаемых сумма x₁ + x₂ + … + x_n приближенно нормальна. Это утверждение называется центральной предельной теоремой теории вероятности.

Приведем строгую формулировку этой теоремы.

Рассмотрим бесконечную последовательность независимых случайных величин x₁, x₂, …, x _n , … с одним и тем же законом распределения, в частности, с одними и теми же параметрами (а, s).

Сумма первых n случайных величин

x₁ + x₂ + … + x _n (38)

имеет числовые характеристики

M = na, D = n s² СКО=s . (39)

Обозначим F_n (х) функцию распределения случайной величины (38). Поставим вопрос: как меняется F_n (х) при неограниченном возрастании числа слагаемых?

Функция распределения нормальной случайной величины с числовыми характеристиками (39) имеет вид (см.§5 главы 4)

,

где Ф (х) – функция Лапласса. Справедлива

Теорема. В указанной ситуации имеет место соотношение

при n ® ¥.

Практически это означает: при достаточно большом числе слагаемых сумма (38) независимых случайных величин с одним и тем же законом распределения с большой точностью подчинена нормальному закону с параметрами (na, s ) независимо от закона распределения слагаемых.

Пример. Определить вероятность того, что продолжи-тельность 100 производственных операций окажется в пределах от 77 до 82 ч., если среднее время одной операции 47,4с., а среднеквадратическое отклонение – 4,9 с.

решение. Обозначим через x _i – случайную величину, равную продолжительности i- ой производственной операции, i = 1, 2, …, 100. Очевидно, по условию а = m = 47, 4 с.,

с. Обозначим через – случайную величину равную продолжительности 100 производственных операций, тогда = x₁ + x₂ + … + x₁₀₀. По условию x _i независимые и однотипные случайные величины, следовательно, из центральной предельной теоремы вытекает, что приближенно нормальна, , и по формуле (19) имеем

Р (77 · 60≤ ≤ 82 · 60) = Р (4620 ≤ ≤ 4920) =

Замечание 1. Эта теорема впервые была доказана в XIXв. немецким математиком Линдебергом. Позднее русским ученым А.М.Ляпуновым утверждение этой теоремы было значительно усилено: оказалось, что в ней требование одинакового закона распределения слагаемых не обязательно.

Приведем нестрогую формулировку теоремы Ляпунова: если случайные величины x₁, x₂, …, x _n независимы и каждая из них не доминирует над остальными, то при достаточно большом числе слагаемых их сумма приближенно нормальна.

Наиболее общая формулировка центральной предельной теоремы была получена русским ученым С.Н.Бернштейном в 20-е годы ХХ века.

Замечание 2. Теорема Ляпунова объясняет причину широкого распространения нормального закона. Действи-тельно, в ряде случаев случайные величины представляют собой результат наложения большого числа независимых небольших случайных факторов. Например, на показание измерительного прибора влияет большое число случайных факторов: колебание температуры, влажность и плотность воздуха, небольшие погрешности при изготовлении и эксплуатации прибора и т. д. Эти факторы независимы и каждый из них не доминирует над остальными, поэтому в силу теоремы Ляпунова показания прибора с большой точностью является нормальной случайной величиной.

Замечание 3. Покажем, что приведенная §6 гл.1 формула Муавра-Лапласа (13) является следствием централь­ной предельной теоремы.

В §2 главы 5 было показано: число успехов в схеме Бернулли может быть представлено в виде суммы (38) независимых случайных величин (индикаторов) с одним и тем же законом распределения и числовыми характеристиками m=np, D=npq.

Из центральной предельной теоремы следует: при достаточно большом числе испытаний число успехов x в схеме Бернулли является с большой точностью нормальной случайной величиной с функцией распределения

.

Откуда получаем

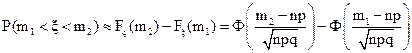
Глава 6. Элементы математической статистики