СОДЕРЖАНИЕ
ВВЕДЕНИЕ. 3
1 МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ ОПТИМИЗАЦИИ.. 4
1.1 Необходимые условия для применения оптимизационных методов. 6
1.2 Определение границ системы.. 6
1.3 Характеристический критерий. 7
1.4 Независимые переменные. 8
1.5 Модель системы.. 9
2 ПРИМЕНЕНИЕ МЕТОДОВ ОПТИМИЗАЦИИ В ИНЖЕНЕРНОЙ ПРАКТИКЕ 11
3 ОПТИМИЗАЦИЯ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.. 13
3.1 Методы прямого поиска. 13
3.2 Критерий оптимальности. 14
3.3 Метод поиска по симплексу (S2-метод) 17
3.4 Алгоритм симплекс-метода. 19
4 РАЗРАБОТКА ОБУЧАЮЩЕЙ ПРОГРАММЫ.. 26
4.1 Текст исходной программы.. 26
4.2 Блок-схема исходной программы.. 37
4.3 Описание руководства по работе с программой. 37
ЗАКЛЮЧЕНИЕ. 42
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.. 43
ПРИЛОЖЕНИЕ. 44
ВВЕДЕНИЕ
Важнейшие задачи, стоящие перед системой высшего образования, заключаются в том, чтобы обеспечить условия и государственные гарантии качества профессионального образования, мобильность выпускников. Перестройка высшего образования, направленная на корректное улучшение качества подготовки специалистов, обусловливает необходимость обновления квалификационных требований к выпускникам высших учебных заведений с учетом последних достижений и перспектив развития науки, техники, производства, образования и культуры. В этой связи разработка новых методов обучения является актуальной проблемой, решение которой напрямую связано с решением вышеозначенных задач.
Целью данной работы являлось разработка обучающих и контролирующих программ, ориентированных на широкое использование информационных технологий.
В работе решались следующие задачи в рамках дисциплины «Методы оптимизации композитных систем»:
1) Обучающие задачи:
а) сформировать знания у будущих специалистов по методологическим основам оптимизации;
б) сформировать знания у будущих специалистов по рациональному выбору методов оптимизации при решении конкретных задач;
в) изучение основ теории оптимизации при решении технических задач;
г) освоение методов оптимизации КС (состава КС, проектирования, конструирования и технологии изготовления изделий из КС);
д) получение практических навыков при постановке оптимизационных задач и путей их решения.
2) Разработка обучающих и контролирующих программ оптимизации функций нескольких переменных.
Пояснительная записка оформлена на примере оптимизации функций нескольких переменных симплекс- методом.
Необходимые условия для применения оптимизационных методов
Для того чтобы использовать математические результаты и численные методы теории оптимизации для решения конкретных инженерных задач, необходимо установить границы подлежащей оптимизации инженерной системы, определить количественный критерий, на основе которого можно произвести анализ вариантов с целью выявления «наилучшего», осуществить выбор внутрисистемных переменных, которые используются для определения характеристик и идентификации вариантов, и, наконец, построить модель, отражающую взаимосвязи между переменными. Эта последовательность действий составляет содержание процесса постановки задачи инженерной оптимизации. Корректная постановка задачи служит ключом к успеху оптимизационного исследования и ассоциируется в большей степени с искусством, нежели с точной наукой. Искусство постановки задач постигается в практической деятельности на примерах успешно реализованных разработок и основывается на четком представлении преимуществ, недостатков и специфических особенностей различных методов теории оптимизации.
Определение границ системы
Прежде чем приступить к оптимизационному исследованию, важно четко определить границы изучаемой системы. Границы системы задаются пределами, отделяющими систему от внешней среды, и служат для выделения системы из ее окружения. При проведении анализа обычно предполагается, что взаимосвязи между системой и внешней средой зафиксированы на некотором выбранном уровне представления. Тем не менее, поскольку такие взаимосвязи всегда существуют, определение границ системы является первым шагом в процессе приближенного описания реальной системы.
В ряде случаев может оказаться, что первоначальный выбор границы является слишком жестким. Для более полного анализа данной инженерной системы может возникнуть необходимость расширения установленных границ системы путем включения других подсистем, оказывающих существенное влияние на функционирование исследуемой системы. производственного цеха. Расширение границ системы повышает размерность и сложность многокомпонентной системы и, следовательно, в значительной мере затрудняет ее анализ. Очевидно, что в инженерной практике следует, насколько это возможно, стремиться к разбиению больших сложных систем на относительно небольшие подсистемы, которые можно изучать по отдельности. Однако при этом необходимо иметь уверенность в том, что такая декомпозиция не приведет к излишнему упрощению реальной ситуации.
Характеристический критерий
Если подлежащая исследованию система определена и ее границы установлены, то на следующем этапе постановки задачи оптимизации необходимо осуществить выбор критерия, на основе которого можно оценить характеристики системы или ее проекта, с тем чтобы выявить «наилучший» проект или множество «наилучших» условий функционирования системы. В инженерных приложениях обычно выбираются критерии экономического характера. Однако спектр возможных формулировок таких критериев весьма широк; при определении критерия могут использоваться такие экономические характеристики, как валовые капитальные затраты, издержки в единицу времени, чистая прибыль в единицу времени, доходы от инвестиций, отношение затрат к прибыли или собственный капитал на данный момент времени. В других приложениях критерий может основываться на некоторых технологических факторах, например, когда требуется минимизировать продолжительность процесса производства изделия, максимизировать темпы производства, минимизировать количество потребляемой энергии, максимизировать величину крутящего момента, максимизировать нагрузку и т. п. Независимо от того, какой критерий выбирается при оптимизации, «наилучшему» варианту всегда соответствует минимальное или максимальноезначение характеристического показателя качества функционирования системы.
Важно отметить, что независимо от содержания оптимизационных методов, рассматриваемых в настоящей книге, только один критерий (и, следовательно, характеристическая мера) может использоваться при определении оптимума, так как невозможно получить решение, которое, например, одновременно обеспечивает минимум затрат, максимум надежности и минимум потребляемой энергии. Здесь мы опять сталкиваемся с существенным упрощением реальной ситуации, поскольку в ряде практических случаев было бы весьма желательным найти решение, которое бы являлось «наилучшим» с позиций нескольких различных критериев.
1. Один из путей учета совокупности противоречивых целевых установок состоит в том, что какой-либо из критериев выбирается в качестве первичного, тогда как остальные критерии считаются вторичными. В этом случае первичный критерий используется при оптимизации как характеристическая мера, а вторичные критерии порождают ограничения оптимизационной задачи, которые устанавливают диапазоны изменений соответствующих показателей от минимального до максимального приемлемого значения.
Критерии не могут быть реализованы при оптимизации одновременно. Приемлемым компромиссом является выбор в качестве первичного характеристического показателя качества функционирования системы подлежащего минимизации показателя суммарных затрат в единицу времени с последующим учетом необходимых вторичных условий, к числу которых относится поддержание объемов складских запасов изделий всех видов в заранее установленных границах,, а также ограничение количества изменений в ассортименте изделий и используемых красок в течение недели.
Независимые переменные
На третьем основном этапе постановки задачи оптимизации осуществляется выбор независимых переменных, которые должны адекватно описывать допустимые проекты или условия функционирования системы. В процессе выбора независимых переменных следует принять во внимание ряд важных обстоятельств.
Во-первых, необходимо провести различие между переменными, значения которых могут изменяться в достаточно широком диапазоне, и переменными, значения которых фиксированы и определяются внешними факторами. Важно провести различие между теми параметрами системы, которые могут предполагаться постоянными, и параметрами, которые подвержены флуктуациям вследствие воздействия внешних или неконтролируемых факторов.
Во-вторых, при постановке задачи следует учитывать все основные переменные, которые влияют на функционирование системы или качество проекта. Независимые переменные должны выбираться таким образом, чтобы все важнейшие технико-экономические решения нашли отражение в формулировке задачи.
Еще одним существенным фактором, влияющим на выбор переменных, является уровень детализации при исследовании системы. Очень важно ввести в рассмотрение все основные независимые переменные, но не менее важно не «перегружать» задачу большим количеством мелких, несущественных деталей. При выборе независимых переменных целесообразно руководствоваться правилом, согласно которому следует рассматривать только те переменные, которые оказывают существенное влияние на характеристический критерий, выбранный для анализа сложной системы.
Модель системы
После того как характеристический критерий и независимые переменные выбраны, на следующем этапе постановки задачи необходимо построить модель, которая описывает взаимосвязи между переменными задачи и отражает влияние независимых переменных на степень достижения цели, определяемой характеристическим критерием. В принципе оптимизационное исследование можно провести на основе непосредственного экспериментирования с системой.
Для этого следует зафиксировать значения независимых внутрисистемных переменных, реализовать процедуру наблюдения за функционированием системы в этих условиях и оценить значение характеристического показателя качества функционирования системы, исходя из зарегистрированных характеристик. Затем с помощью оптимизационных методов можно скорректировать значения независимых переменных и продолжить серию экспериментов. Однако на практике оптимизационные исследования проводятся, как правило, на основе упрощенного математического представления системы, которое носит название модели.Применение моделей обусловлено тем, что эксперименты с реальными системами обычно требуют слишком больших затрат средств и времени, а также в ряде случаев оказываются связанными с риском. Модели широко используются при инженерном проектировании, поскольку это открывает возможности для реализации наиболее экономичного способа изучения влияния изменений в значениях основных независимых переменных на показатель качества функционирования системы.
В самом общем представлении структура модели включает основные уравнения материальных и энергетических балансов, соотношения, связанные с проектными решениями, а также уравнения, описывающие физические процессы, протекающие в системе. Эти уравнения обычно дополняются неравенствами, которые определяют область допустимых значений независимых переменных, позволяют определить требования, накладываемые на верхние или нижние границы изменения характеристик функционирования системы, и установить лимиты имеющихся ресурсов. Таким образом, элементы модели содержат всю информацию, которая обычно используется при расчете проекта или прогнозировании характеристик инженерной системы. Очевидно, что процесс построения модели является весьма трудоемким и требует четкого понимания специфических особенностей рассматриваемой системы. В общем случае модель представляет собой некоторый набор уравнений и неравенств, которые определяют взаимосвязь между переменными системы и ограничивают область допустимых изменений переменных.
Методы прямого поиска
Многомерные методы, реализующие процедуру поиска оптимума на основе вычисления значений функции, с общих позиций можно разделить на эвристические и теоретические. Эвристические методы, как это следует из названия, реализуют процедуры поиска с помощью интуитивных геометрических представлений и обеспечивают получение частных эмпирических результатов. С другой стороны, теоретические методы основаны на фундаментальных математических теоремах и обладают такими операционными свойствами, как сходимость (по крайней мере при выполнении некоторых определенных условий). Ниже рассматриваются три метода прямого поиска:
1) поиск по симплексу, или S2-метод;
2) метод поиска Хука — Дживса;
3) метод сопряженных направлений Пауэлла.
Первые два из перечисленных методов относятся к категории эвристических и реализуют принципиально различающиеся стратегии поиска. В процессе поиска по S2-методу последовательно оперируют регулярными симплексами в пространстве управляемых переменных, тогда как при реализации метода Хука— Дживса используется фиксированное множество (координатных) направлений, выбираемых рекурсивным способом. Метод Пауэлла основан на теоретических результатах и ориентирован на решение задач с квадратичными целевыми функциями; для таких задач метод сходится за конечное число итераций. К числу общих особенностей всех трех методов следует отнести относительную простоту соответствующих вычислительных процедур, которые легко реализуются и быстро корректируются.
Критерий оптимальности
Сначала рассмотрим вопрос анализа «в статике» с использованием положений линейной алгебры и дифференциального исчисления, а также условия, которые (в достаточно общих возможных ситуациях) позволяют идентифицировать точки оптимума. Такие условия используются для проверки выбранных точек и дают возможность выяснить, являются ли эти точки точками минимума, максимума или седловыми точками. При этом задача выбора указанных точек остаётся вне рамок проводимого анализа; основное внимание уделяется решению вопроса о том, соответствуют ли исследуемые точки решениям многомерной задачи безусловной оптимизации, в которой требуется
минимизировать f(х), xÎRN, (3.1)
при отсутствии ограничений на х, где х — вектор управляемых переменных размерности N, f — скалярная целевая функция. Обычно предполагается, что xi (для всех значений i = 1, 2, 3,…, N)могут принимать любые значения, хотя в ряде практических приложений область значений х выбирается в виде дискретного множества. Кроме того, часто оказывается удобным предполагать, что функция f и ее производные существуют и непрерывны всюду, хотя известно, что оптимумы могут достигаться в точках разрыва f или ее градиента
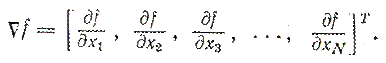
 (3.2)
(3.2)
Функция f может принимать минимальное значение в точке 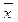 , в которой f или
, в которой f или 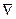 f претерпевают разрыв. Кроме того, в этой точке
f претерпевают разрыв. Кроме того, в этой точке 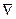 f может не существовать. Для того чтобы построить систему конструктивных критериев оптимальности, необходимо (по крайней мере на первой стадии исследования) исключить из рассмотрения подобные ситуации, которые весьма усложняют анализ. Наконец, в ряде случаев приходится ограничиваться лишь идентификацией локальных оптимумов, поскольку нелинейная целевая функция f не всегда обладает свойством выпуклости и, следовательно, может оказаться мультимодальной.
f может не существовать. Для того чтобы построить систему конструктивных критериев оптимальности, необходимо (по крайней мере на первой стадии исследования) исключить из рассмотрения подобные ситуации, которые весьма усложняют анализ. Наконец, в ряде случаев приходится ограничиваться лишь идентификацией локальных оптимумов, поскольку нелинейная целевая функция f не всегда обладает свойством выпуклости и, следовательно, может оказаться мультимодальной.
Далее перейдем к вопросу анализа «в динамике», который формулируется следующим образом: если точка х(0) не удовлетворяет условиям, налагаемым упомянутыми выше критериями оптимальности, то как получить «хорошее» новое приближение x (1)к решению х *? Попытка дать ответ на этот вопрос приводит к необходимости рассмотрения ряда методов, описание которых составляет значительную часть данной главы. Рассматриваемые методы классифицируются в соответствии с тем, используется ли информация о производных исследуемых функций.
Рассматрим условия, которые позволяют характеризовать (т. е. классифицировать) точки пространства управляемых переменных. Критерии оптимальности необходимы для распознавания решений и, кроме того, составляют основу большинства используемых методов поиска решений. Рассмотрим разложение Тейлора для функции нескольких переменных:
f(x)=f( )+
)+ 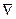 f(
f( )
) 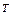 ∆x+½∆x
∆x+½∆x 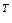
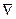
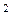 f(
f( )∆x+O
)∆x+O 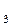 (∆x), (3.3)
(∆x), (3.3)
где  — точка разложения из пространства RN; ∆ х = х -
— точка разложения из пространства RN; ∆ х = х -  — величина изменения х;
— величина изменения х; 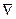 f(x) — N-мерный вектор-столбец первых производных f(х), вычисленных в точке
f(x) — N-мерный вектор-столбец первых производных f(х), вычисленных в точке  ;
; 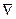
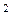 f(
f( ) = H
) = H 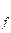 (
( ) — симметрическая матрица порядка N × N вторых частных производных f(x), вычисленных в точке
) — симметрическая матрица порядка N × N вторых частных производных f(x), вычисленных в точке  . (Эту матрицу часто называют матрицей Гессе. Ее элемент, расположенный на пересечении i -й строки и j -го столбца, равен
. (Эту матрицу часто называют матрицей Гессе. Ее элемент, расположенный на пересечении i -й строки и j -го столбца, равен 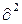 f / dx
f / dx 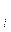
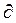 x
x 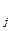 .) O
.) O 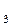 (∆x) — сумма всех членов разложения, имеющих порядок по ∆x выше второго. Пренебрегая членами высших порядков (т. е. исключая O
(∆x) — сумма всех членов разложения, имеющих порядок по ∆x выше второго. Пренебрегая членами высших порядков (т. е. исключая O 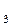 (∆x)), определим величину изменения целевой функции f (х), соответствующего произвольному изменению х:
(∆x)), определим величину изменения целевой функции f (х), соответствующего произвольному изменению х:
∆ f(x)= f(x) - f( ) =
) = 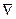 f(
f( )
) 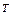 ∆x+½∆x
∆x+½∆x 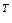
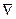
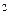 f(
f( )∆x (3.4)
)∆x (3.4)
Напомним, что по определению во всех точках из окрестности точки минимума целевая функция принимает значения, которые превышают минимальное, т. е. имеет место неравенство
∆f = f(x) - f( ) ≥0. (3.5)
) ≥0. (3.5)
Точка  является точкой глобального минимума, если неравенство (3.5) выполняется для всех хÎ RN; такие точки будем обозначать через х**. Когда формула (3.5) справедлива лишь в некоторой δ-окрестности точки
является точкой глобального минимума, если неравенство (3.5) выполняется для всех хÎ RN; такие точки будем обозначать через х**. Когда формула (3.5) справедлива лишь в некоторой δ-окрестности точки  , т. е. для всех х, таких, что || х –
, т. е. для всех х, таких, что || х –  || < δ при заданном δ > 0, то
|| < δ при заданном δ > 0, то  есть точка локального минимума, или х *. Если же
есть точка локального минимума, или х *. Если же
∆ f = f(x) – f( ) ≤0. (3.6)
) ≤0. (3.6)
то  есть точка максимума (локального или глобального в соответствии с данными выше определениями). Исключение знака равенства из формул (3.5) и (3.6) позволяет определить точку строгого минимума или максимума. В случае когда ∆f принимает как положительные и отрицательные, так и нулевые значения в зависимости от выбора точек из δ-окрестности, точка
есть точка максимума (локального или глобального в соответствии с данными выше определениями). Исключение знака равенства из формул (3.5) и (3.6) позволяет определить точку строгого минимума или максимума. В случае когда ∆f принимает как положительные и отрицательные, так и нулевые значения в зависимости от выбора точек из δ-окрестности, точка  представляет собой седловую точку.
представляет собой седловую точку.
Вернемся к равенству (3.4) и вспомним о выдвинутом ранее предположении о том, что f(х), 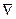 f(x) и
f(x) и 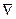
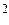 f(x) существуют и непрерывны для всех х Î RN. Как следует из формулы (3.4), для того чтобы знак ∆f не менялся при произвольном варьировании ∆х, градиент
f(x) существуют и непрерывны для всех х Î RN. Как следует из формулы (3.4), для того чтобы знак ∆f не менялся при произвольном варьировании ∆х, градиент 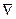 f(
f( ) должен быть равен нулю, т. е.
) должен быть равен нулю, т. е.  должна быть стационарной точкой. В противном случае разность ∆f может принимать положительные или отрицательные значения в зависимости от знаков
должна быть стационарной точкой. В противном случае разность ∆f может принимать положительные или отрицательные значения в зависимости от знаков 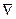 f(
f( ) и ∆х. Таким образом, точка
) и ∆х. Таким образом, точка  должна удовлетворять условию стационарности
должна удовлетворять условию стационарности
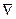 f(
f( ) = 0, (3.7)
) = 0, (3.7)
и формула (3.4) принимает следующий вид:
∆f(x) = +½∆x 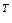
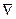
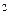 f(
f( )∆x. (3.8)
)∆x. (3.8)
Очевидно, что знак ∆f(x) определяется квадратичной формой
Q (х) = ∆x 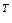
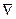
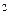 f(
f( )∆x (3.9)
)∆x (3.9)
или Q(z)=zTAz.
Из линейной алгебры известно, что
А — положительно определенная матрица, если Q(z)>0 для любых z;
А — положительно полуопределенная матрица, если Q (z)≥0 для любых z;
А — отрицательно определенная матрица, если Q(z)<0 для любых z; (3.10)
А — отрицательно полуопределенная матрица, если Q(z)≤0 для любых z;
А — неопределенная матрица, если Q (z)>0 для некоторых z и Q(z)<0 для остальных z.
Из (3.10) следует, что стационарная точка  есть
есть
точка минимума, если 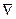 2f(
2f( ) — положительно полуопределенная матрица;
) — положительно полуопределенная матрица;
точка максимума, если 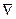 2f(
2f( ) — отрицательно полуопределенная матрица; (3.11)
) — отрицательно полуопределенная матрица; (3.11)
cедловая точка, если 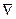 2f(x)
2f(x)  0 — неопределенная матрица.
0 — неопределенная матрица.
3.3 Метод поиска по симплексу (S2-метод)
Первые попытки решения оптимизационных задач без ограничений на основе прямого поиска связаны с использованием одномерных методов оптимизации. Как правило, при реализации таких методов допустимая область определения показателя качества функционирования системы (целевой функции) заменяется дискретным множеством (решеткой) точек пространства управляемых переменных, а затем используются различные стратегии уменьшения области, которая содержит решение задачи. Часто эта процедура оказывается эквивалентной равномерному поиску в узлах решетки и, следовательно, непригодной для решения задач с числом переменных, превышающим 2. Более полезная идея заключается в выборе базовой точки и оценивании значений целевой функции в точках, окружающих базовую точку. Например, при решении задачи с двумя переменными можно воспользоваться квадратным образцом, изображенным на рис. 3.1. Затем «наилучшая» из пяти исследуемых точек выбирается в качестве следующей базовой точки, вокруг которой строится, аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца следует уменьшить, после чего продолжить поиск.
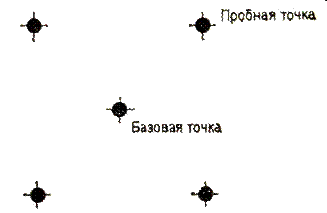
Рисунок 3.1 - Квадратный образец (частный случай кубического образца)
Этот тип эволюционной оптимизации был использован Боксом и другими исследователями для анализа функционирования промышленных предприятий, когда эффект варьирования значений переменных, описывающих производственные процессы, измеряется с ошибкой. В задачах большой размерности вычисление значений целевой функции проводится во всех вершинах, а также в центре тяжести гиперкуба, т. е. в точках так называемого кубического образца. Если количество переменных (размерность пространства, в котором ведется поиск) равно N, то поиск по кубическому образцу требует 2 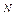 +1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вычислений значения целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.
+1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вычислений значения целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.
Одна из вызывающих особый интерес стратегий поиска положена в основу метода поиска по симплексу, предложенного Спендли, Хекстом и Химсвортом. Следует отметить, что указанный метод и другие подобные методы не имеют отношения к симплекс-методу линейного программирования, а сходство названий носит случайный характер. Процедура симплексного поиска Спендли, Хекста и Химсворта базируется на том, что экспериментальным образцом, содержащим наименьшее количество точек, является регулярный симплекс. Регулярный симплекс в N-мерном пространстве представляет собой многогранник, образованный N+1 равностоящими друг от друга точками-вершинами.
Например, в случае двух переменных симплексом является равносторонний треугольник; в трехмерном пространстве симплекс представляет собой тетраэдр. В алгоритме симплексного поиска используется важное свойство симплексов, согласно которому новый симплекс можно построить на любой грани начального симплекса путем переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведенной через центр тяжести остальных вершин начального симплекса. Полученная таким образом точка является вершиной нового симплекса, а выбранная при построении вершина начального симплекса исключается. Нетрудно видеть, что при переходе к новому симплексу требуется одно вычисление значения целевой функции. Рис. 3.2 иллюстрирует процесс построения нового симплекса на плоскости.
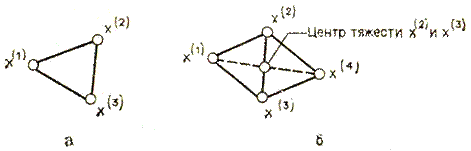
a — начальный симплекс; x(1), x(2), x(3); б — новый симплекс; x(2),x(3), x(4)
Рисунок 3.2 - Построение нового симплекса
Алгоритм симплекс-метода
Работа алгоритма симплексного поиска начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой из вершин симплекса. При этом определяется вершина, которой соответствует наибольшее значение целевой функции. Затем найденная вершина проецируется через центр тяжести остальных вершин симплекса в новую точку, которая используется в качестве вершины нового симплекса. Если функция убывает достаточно плавно, итерации продолжаются до тех пор, пока либо не будет накрыта точка минимума, либо не начнется циклическое движение по двум или более симплексам. В таких ситуациях можно воспользоваться следующими тремя правилами.
Текст исходной программы
В данном разделе приведен листинг исходной программы для изучения метода оптимизации функции нескольких переменных с использованием симплекс-метода.
Dim Proba As Boolean
Private Sub Pause()
' Создаём цикл, который работает до тех пор,
' пока мы не нажмём кнопку "Далее"
Do
DoEvents
If Proba = True Then
Exit Do
End If
Loop
Proba = False
End Sub
Private Sub cmdNext_Click()
' Остановка цикла
Proba = True
End Sub
Private Sub visib()
cmdRun.Visible = True
cmdRefresh.Visible = False
cmdNext.Visible = False
Proba = True
End Sub
Private Sub cmdRefresh_Click()
lblComment1 = ""
lblComment2 = ""
lblComment3 = ""
txtFunction = ""
txtMM = ""
txtX1 = ""
txtX2 = ""
End Sub
Private Sub cmdRun_Click()
cmdRun.Visible = False
cmdRefresh.Visible = True
cmdNext.Visible = True
Proba = False
'Проверяем на наличие данных
If txtFunction = "" Then
MsgBox "Введите функцию!"
Call visib
Exit Sub
ElseIf txtMM = "" Then
MsgBox "Введите масштабный множитель!"
Call visib
Exit Sub
ElseIf txtX1 = "" Then
MsgBox "Введите X1"
Call visib
Exit Sub
ElseIf txtX2 = "" Then
MsgBox "Введите X2"
Call visib
Exit Sub
End If
'Вводим исходные данные
Dim Otklick As Variant
Dim MM As Variant
Dim X01 As Variant
Dim X02 As Variant
Dim Prirash1 As Variant
Dim Prirash2 As Variant
Dim X11 As Variant
Dim X12 As Variant
Dim X21 As Variant
Dim X22 As Variant
lblComment1 = "Определение приращений p1 и p2"
lblComment2 = "p1 = ((N+1)^0,5 + N - 1) / (N * 2^0,5)) * M; p2 = ((N+1)^0,5 - 1) / (N * 2^0,5)) * M, где N - размерность задачи, M - масштабный множитель."
MM = Val(txtMM.Text)
X01 = Val(txtX1.Text)
X02 = Val(txtX2.Text)
Prirash1 = ((Sqr(3) + 1) / (2 * Sqr(2))) * MM
Prirash2 = ((Sqr(3) - 1) / (2 * Sqr(2))) * MM
lblComment3 = "p1 = ((2+1)^0,5 + 2 - 1) / (2 * 2^0,5)) * " & MM & "= " & Prirash1 & "; p2 = ((2+1)^0,5 - 1) / (2 * 2^0,5)) * " & MM & "= " & Prirash2
Call Pause
lblComment1 = "Вычисляем координаты двух остальных вершин симплекса"
lblComment2 = "Х1,1 = Х0,1 + р2; Х1,2 = Х0,2 + р1; Х2,1 = Х0,1 + р1; Х2,2 = Х0,2 + р2"
X11 = X01 + Prirash2
X12 = X01 + Prirash1
X21 = X01 + Prirash1
X22 = X01 + Prirash2
lblComment3 = "X1,1 = " & X01 & " + " & Prirash2 & " = " & X11 & "; X1,2 = " & X02 & " + " & Prirash1 & " = " & X12 & "; X2,1 = " & X01 & " + " & Prirash1 & " = " & X21 & "; x2,2 = " & X02 & " + " & Prirash2 & " = " & X22
Call Pause
lblComment1 = "Вычисляем значения функции в каждой из вершин симплекса"
'создаём лист XL
Dim ExcelSheet As Object
Set ExcelSheet = CreateObject("Excel.Sheet")
' Make Excel visible through the Application object.
ExcelSheet.Application.Visible = False
' Place some text in the first cell of the sheet.
'заносим начальные значения и считаем их в ХL-e
ExcelSheet.Application.range("X1").Value = X01
ExcelSheet.Application.range("X2").Value = X02
ExcelSheet.Application.range("A3").Value = "=" & txtFunction
Dim ZnachFunctionX0 As Variant
ZnachFunctionX0 = ExcelSheet.Application.range("A3").Value
ExcelSheet.Application.range("X1").Value = X11
ExcelSheet.Application.range("X2").Value = X12
Dim ZnachFunctionX1 As Variant
ZnachFunctionX1 = ExcelSheet.Application.range("A3").Value
ExcelSheet.Application.range("X1").Value = X21
ExcelSheet.Application.range("X2").Value = X22
Dim ZnachFunctionX2 As Variant
ZnachFunctionX2 = ExcelSheet.Application.range("A3").Value
lblComment2 = "f(X0,1; X0,2) = f(" & X01 & "; " & X02 & ") = " & ZnachFunctionX0 & "; f(X1,1; X1,2)=f(" & X11 & "; " & X12 & ") = " & ZnachFunctionX1 & "; f(X2,1; X2,2)=f(" & X21 & "; " & X22 & ") = " & ZnachFunctionX2
lblComment3 = ""
Call Pause
lblComment1 = "Отражение точки"
Dim X31 As Variant
Dim X32 As Variant
Dim ZnachFunctionX3 As Variant
Dim i As Integer
i = 3
Dim j As Integer
j = 0
Dim k As Integer
k = 1
Dim z As Integer
z = 2
Dim X01Copy As Variant
Dim X02Copy As Variant
Dim X11Copy As Variant
Dim X12Copy As Variant
Dim X21Copy As Variant
Dim X22Copy As Variant
Do
If ZnachFunctionX0 > ZnachFunctionX1 And ZnachFunctionX0 > ZnachFunctionX2 Then
If i = j + 1 Then
lblComment1 = "Остановка поиска"
lblComment2 = "f(X" & j & ",1; Х" & j & ",2)>f(X" & k & ",1; Х" & k & ",2) и f(X" & j & ",1; Х" & j & ",2)>f(X" & z & ",1; Х" & z & ",2);" & ZnachFunctionX0 & ">" & ZnachFunctionX1 & " и " & ZnachFunctionX0 & " > " & ZnachFunctionX2 & ", следовательно необходимо отразить точку с коодинатами (Х" & j & ",1; Х" & j & ",2), (" & X01 & "; " & X02 & ") относительно центра тяжести двух остальных вершин симплекса"
X01Copy = X01
X02Copy = X02
X01 = X11 + X21 - X01
X02 = X12 + X22 - X02
lblComment3 = "Х" & i & "1 = Х" & k & "1 + Х" & z & "1 - Х" & j & "1 = " & X11 & " + " & X21 & " - " & X01Copy & " = " & X01 & ";Х" & i & "2 = Х" & k & "2 + Х" & z & "2 - Х" & j & "2 = " & X12 & " + " & X22 & " - " & X02Copy & " = " & X02 & ". Поиск останавливается, т. к. эта вершина симплекса встречалась на предыдущей итерации."
Call Pause
ExcelSheet.Application.range("X1").Value = X01
ExcelSheet.Application.range("X2").Value = X02
ZnachFunctionX0 = ExcelSheet.Application.range("A3").Value
lblComment2 = "Оптимум находится внутри симплекса с вершинами (Х" & j & "1, X" & j & "2); (Х" & k & "1), X" & k & "2); (X" & z & "1, X" & z & "2); (" & X01 & "; " & X02 & "); (" & X11 & "; " & X12 & "); (" & X21 & "; " & X22 & ")."
lblComment3 = "f(Х" & j & "1, X" & j & "2) = " & ZnachFunctionX0 & "; f(Х" & k & "1, X" & k & "2) = " & ZnachFunctionX1 & "; f(X" & z & "1, X" & z & "2) =" & ZnachFunctionX2 & "."
Exit Do
End If
lblComment2 = "f(X" & j & ",1; Х" & j & ",2)>f(X" & k & ",1; Х" & k & ",2) и f(X" & j & ",1; Х" & j & ",2)>f(X" & z & ",1; Х" & z & ",2);" & ZnachFunctionX0 & ">" & ZnachFunctionX1 & " и " & ZnachFunctionX0 & " > " & ZnachFunctionX2 & ", следовательно необходимо отразить точку с коодинатами (Х" & j & ",1; Х" & j & ",2), (" & X01 & "; " & X02 & ") относительно центра тяжести двух остальных вершин симплекса"
X01Copy = X01
X02Copy = X02
X01 = X11 + X21 - X01
X02 = X12 + X22 - X02
lblComment3 = "Х" & i & "1 = Х" & k & "1 + Х" & z & "1 - Х" & j & "1 = " & X11 & " + " & X21 & " - " & X01Copy & " = " & X01 & ";Х" & i & "2 = Х" & k & "2 + Х" & z & "2 - Х" & j & "2 = " & X12 & " + " & X22 & " - " & X02Copy & " = " & X02
ExcelSheet.Application.range("X1").Value = X01
ExcelSheet.Application.range("X2").Value = X02
ZnachFunctionX0 = ExcelSheet.Application.range("A3").Value
j = i
GoTo 10
ElseIf ZnachFunctionX1 > ZnachFunctionX0 And ZnachFunctionX1 > ZnachFunctionX2 Then
If i = k + 1 Then
lblComment1 = "Остановка поиска"
lblComment2 = "f(X" & k & ",1; Х" & k & ",2)>f(X" & j & ",1; Х" & j & ",2) и f(X" & k & ",1; Х" & k & ",2)>f(X" & z & ",1; Х" & z & ",2);" & ZnachFunctionX1 & ">" & ZnachFunctionX0 & " и " & ZnachFunctionX1 & " > " & ZnachFunctionX2 & ", следовательно необходимо отразить точку с коодинатами (Х" & k & ",1; Х" & k & ",2), (" & X11 & "; " & X12 & ") относительно центра тяжести двух остальных вершин симплекса"
X11Copy = X11
X12Copy = X12
X11 = X01 + X21 - X11
X12 = X02 + X22 - X12
lblComment3 = "Х" & i & "1 = Х" & j & "1 + Х" & z & "1 - Х" & k & "1 = " & X01 & " + " & X21 & " - " & X11Copy & " = " & X11 & ";Х" & i & "2 = Х" & j & "2 + Х" & z & "2 - Х" & k & "2 = " & X02 & " + " & X22 & " - " & X12Copy & " = " & X12 & ". Поиск останавливается, т. к. эта вершина симплекса встречалась на предыдущей итерации."
Call Pause
ExcelSheet.Application.range("X1").Value = X11
ExcelSheet.Application.range("X2").Value = X12
ZnachFunctionX1 = ExcelSheet.Application.range("A3").Value
lblComment2 = "Оптимум находится внутри симплекса с вершинами (Х" & j & "1, X&q



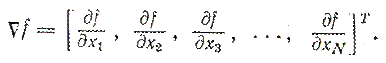
 (3.2)
(3.2)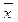 , в которой f или
, в которой f или 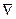 f претерпевают разрыв. Кроме того, в этой точке
f претерпевают разрыв. Кроме того, в этой точке  )+
)+ 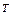 ∆x+½∆x
∆x+½∆x 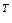
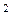 f(
f(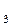 (∆x), (3.3)
(∆x), (3.3)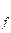 (
(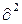 f / dx
f / dx 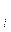
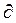 x
x 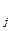 .) O
.) O 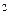 f(
f(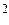 f(x) существуют и непрерывны для всех х Î RN. Как следует из формулы (3.4), для того чтобы знак ∆f не менялся при произвольном варьировании ∆х, градиент
f(x) существуют и непрерывны для всех х Î RN. Как следует из формулы (3.4), для того чтобы знак ∆f не менялся при произвольном варьировании ∆х, градиент  0 — неопределенная матрица.
0 — неопределенная матрица.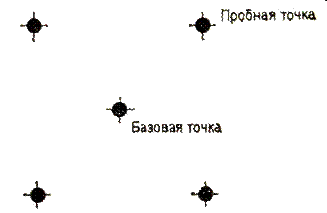
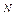 +1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вычислений значения целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.
+1 вычислений значения функций для одного образца. При увеличении размерности задачи необходимое количество вычислений значения целевой функции возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.



