Прямая  и плоскость
и плоскость  перпендикулярны при значениях
перпендикулярны при значениях  и
и 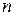 , равных …
, равных …
Решение:
Прямая перпендикулярна плоскости, если направляющий вектор прямой  и нормальный вектор плоскости
и нормальный вектор плоскости  коллинеарны и, следовательно, их координаты пропорциональны:
коллинеарны и, следовательно, их координаты пропорциональны:  .
.
Тема: Прямая линия в пространстве
Дана прямая 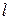 , заданная уравнением
, заданная уравнением  , и плоскость
, и плоскость  , заданная уравнением
, заданная уравнением  . Тогда прямая
. Тогда прямая 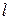 …
…
1. пересекает плоскость  под острым углом;
под острым углом;
2. принадлежит плоскости  ;
;
3. перпендикулярна плоскости  ;
;
4. параллельна плоскости  .
.
Решение:
Направляющий вектор прямой  и нормальный вектор плоскости
и нормальный вектор плоскости  . Скалярное произведение векторов
. Скалярное произведение векторов  . Поэтому эти векторы взаимно перпендикулярны, а это означает, что прямая
. Поэтому эти векторы взаимно перпендикулярны, а это означает, что прямая 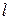 либо параллельна плоскости
либо параллельна плоскости  , либо принадлежит плоскости
, либо принадлежит плоскости  . Точка
. Точка  принадлежит прямой
принадлежит прямой 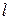 , но не принадлежит плоскости
, но не принадлежит плоскости  :
:  . Поэтому прямая
. Поэтому прямая 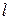 параллельна плоскости
параллельна плоскости  .
.
Тема: Прямая линия в пространстве
Прямая  параллельна плоскости
параллельна плоскости 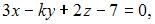 если параметр
если параметр 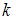 равен …
равен …
Решение:
Прямая параллельна плоскости, если скалярное произведение направляющего вектора прямой  и нормального вектора плоскости
и нормального вектора плоскости  равно нулю, то есть векторы перпендикулярны. Тогда
равно нулю, то есть векторы перпендикулярны. Тогда  или
или 
Тема: Прямая линия в пространстве
Угол  между прямой
между прямой  и плоскостью
и плоскостью  равен …
равен …
Решение:
Синус угла между прямой  и плоскостью
и плоскостью 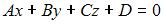 находится как
находится как
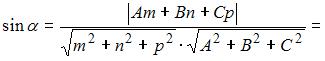

Тогда острый угол между прямой и плоскостью 
Тема: Прямая линия в пространстве
Угол  между прямой
между прямой  и плоскостью
и плоскостью  равен …
равен …
Выберите один из 4 вариантов ответа:
1) 
2) 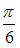
3) 
4) 
Верный ответ (1 б.): 1;
Тема: Прямая линия в пространстве
Точка пересечения прямой 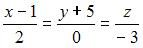 и плоскости
и плоскости  имеет координаты …
имеет координаты …
Решение:
Запишем уравнение прямой в параметрическом виде:
 то есть
то есть 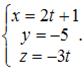
Подставим полученные уравнения в уравнение плоскости  .
.
Тогда  или
или  Подставляя значение параметра
Подставляя значение параметра  в систему параметрических уравнений
в систему параметрических уравнений  найдем координаты точки пересечения прямой и плоскости
найдем координаты точки пересечения прямой и плоскости 
Тема: Прямая линия в пространстве
Даны прямая линия l, заданная уравнением  и плоскость
и плоскость 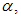 заданная уравнением
заданная уравнением 
Тогда прямая l …
Выберите один из 4 вариантов ответа:
1) параллельна плоскости 
2) принадлежит плоскости 
3) перпендикулярна плоскости 
4) пересекает плоскость  под острым углом
под острым углом
Верный ответ (1 б.): 1;
Вопрос:
Расстояние между прямой  и плоскостью
и плоскостью  равно …
равно …
Выберите один из 4 вариантов ответа:
1) 3
2) 18
3) 0
4) 15
Верный ответ (1 б.): 1;
Задание # 76 - ошибка!
Вопрос:
Параметрические уравнения прямой, параллельной оси Oy и проходящей через точку  имеют вид …
имеют вид …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 
Верный ответ (1 б.): 1;
Задание # 77 - ошибка!
Вопрос:
Каноническое уравнение прямой, проходящей через начало координат перпендикулярно прямым  и
и  имеет вид …
имеет вид …
Выберите один из 4 вариантов ответа:
1) 
2) 
3) 
4) 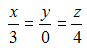
Верный ответ (1 б.): 1;
Тема: Прямая линия в пространстве
Уравнение перпендикуляра, опущенного из точки  на ось
на ось  имеет вид …
имеет вид …
Решение:
Перпендикуляр, опущенный из точки  на ось
на ось  пересекает ее в точке
пересекает ее в точке  Уравнение прямой, проходящей через точки
Уравнение прямой, проходящей через точки  и
и  имеет вид
имеет вид  Тогда
Тогда 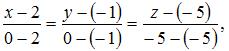 или
или 



 и плоскость
и плоскость  перпендикулярны при значениях
перпендикулярны при значениях  и
и 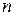 , равных …
, равных … и нормальный вектор плоскости
и нормальный вектор плоскости  коллинеарны и, следовательно, их координаты пропорциональны:
коллинеарны и, следовательно, их координаты пропорциональны:  .
.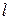 , заданная уравнением
, заданная уравнением  , и плоскость
, и плоскость  , заданная уравнением
, заданная уравнением  . Тогда прямая
. Тогда прямая  и нормальный вектор плоскости
и нормальный вектор плоскости  . Скалярное произведение векторов
. Скалярное произведение векторов  . Поэтому эти векторы взаимно перпендикулярны, а это означает, что прямая
. Поэтому эти векторы взаимно перпендикулярны, а это означает, что прямая  принадлежит прямой
принадлежит прямой  . Поэтому прямая
. Поэтому прямая  параллельна плоскости
параллельна плоскости 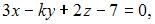 если параметр
если параметр 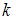 равен …
равен …

 и нормального вектора плоскости
и нормального вектора плоскости  равно нулю, то есть векторы перпендикулярны. Тогда
равно нулю, то есть векторы перпендикулярны. Тогда  или
или 
 между прямой
между прямой  и плоскостью
и плоскостью  равен …
равен …

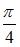

 и плоскостью
и плоскостью 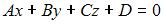 находится как
находится как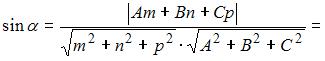


 между прямой
между прямой  и плоскостью
и плоскостью  равен …
равен …
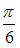


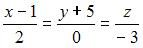 и плоскости
и плоскости  имеет координаты …
имеет координаты …



 то есть
то есть 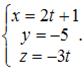
 или
или  Подставляя значение параметра
Подставляя значение параметра  в систему параметрических уравнений
в систему параметрических уравнений  найдем координаты точки пересечения прямой и плоскости
найдем координаты точки пересечения прямой и плоскости 
 и плоскость
и плоскость 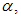 заданная уравнением
заданная уравнением 

 и плоскостью
и плоскостью  равно …
равно … имеют вид …
имеют вид …



 и
и  имеет вид …
имеет вид …


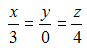
 на ось
на ось  имеет вид …
имеет вид …

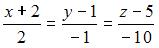

 на ось
на ось  пересекает ее в точке
пересекает ее в точке  Уравнение прямой, проходящей через точки
Уравнение прямой, проходящей через точки  и
и  имеет вид
имеет вид  Тогда
Тогда 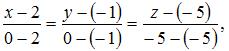 или
или 



