Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
 2024-02-15 |
 19 |
из
5.00
|
Заказать работу |
ИНТЕГРАЛОВ
Цель:
- сформировать навыки приближённого вычисления определённых интегралов c заданной точностью;
- развить умение находить значения функций в заданных точках;
- закрепить знания о формулах приближённых вычислений;
Материально – техническое обеспечение: методические указания по выполнению работы, микрокалькуляторы;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
Приближенные методы вычисления определенного интеграла в большинстве случаев основаны на том, что определенный интеграл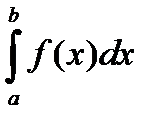 
численно равен площади криволинейной трапеции, ограниченной кривой 
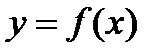, сегментом оси ОХ и вертикальными прямым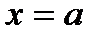и 
и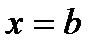 
, проведенными через эти точки. Благодаря этому задача о приближенном вычислении интеграла равносильна задаче о приближенном вычислении площади криволинейной трапеции.
Идея приближенного вычисления интеграла заключается в том, что кривая заменяется новой, достаточно «близкой» к ней кривой. В зависимости от выбора новой кривой мы получим ту или иную приближенную формулу интегрирования.
1. Формула прямоугольников:
,
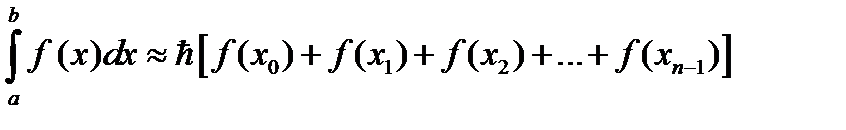где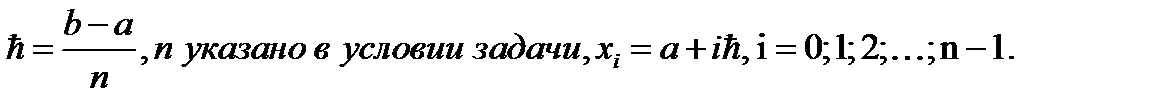 
2. Формула трапеций:
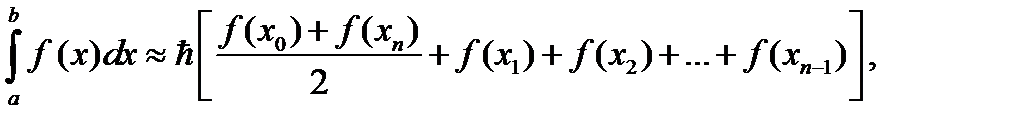
где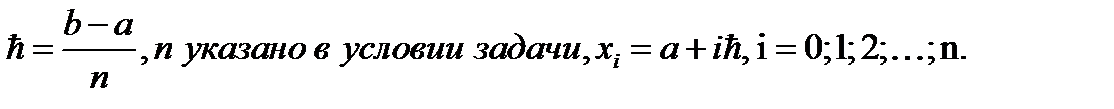 
3. Формула параболических трапеций (формула Симпсона):
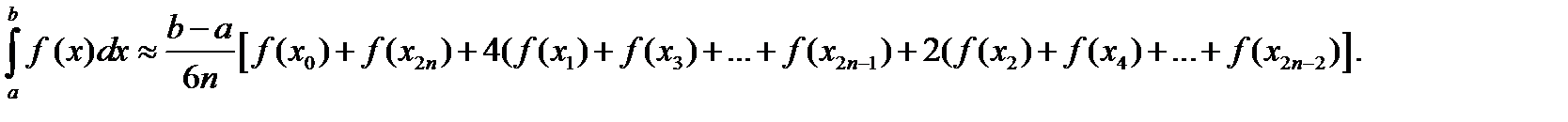
Пример 1. Найти приближенное значение интеграла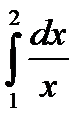 
, вычисленное по формуле прямоугольников при n=10 с точностью до 0,001:
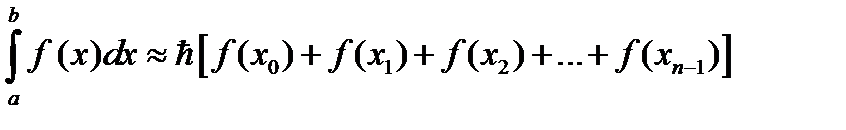
Решение. По условию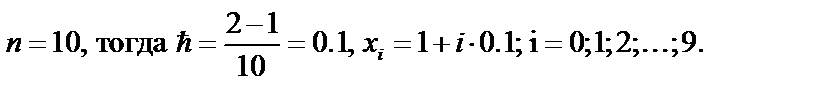 
Найдём значения аргументов х i и соответствующие значения функции f( xi) c шагом 0,1:
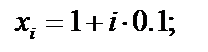
| f( xi)= 1 ∕х i |
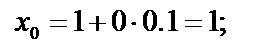
| f ( x0 )= 1 ∕х 0 = 1 ∕ 1=1 |
| f ( x 1 )= 1 ∕х1=1 ∕1. 1 ≈ 0.909 |
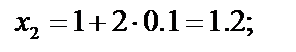
| f ( x2 )= 1 ∕х 2 =1 ∕1 .2 ≈ 0.833 |
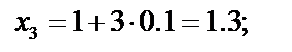
| f ( x3 )= 1 ∕х 3 =1 ∕1 .3 ≈ 0.769 |
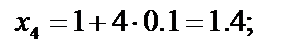
| f ( x4 )= 1 ∕х 4 = 1 ∕ 1.4 ≈ 0.714 |
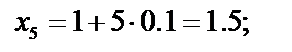
| f ( x5 )= 1 ∕х 5 = 1 ∕ 1.5 ≈ 0.667 |
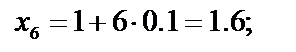
| f ( x6 )= 1 ∕х 6 = 1 ∕ 1.6 ≈ 0.625 |
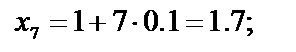
| f ( x7 )= 1 ∕х 7 = 1 ∕ 1.7 ≈ 0.588 |
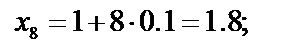
| f ( x8 )= 1 ∕х 8 = 1 ∕ 1.8 ≈ 0.556 |
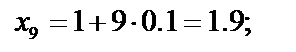
| f ( x9 )= 1 ∕х 9 = 1 ∕ 1.9 ≈ 0.526 |
Подставим найденные значения в формулу прямоугольников и вычислим приближённое значение интеграла с точностью до 0,001:
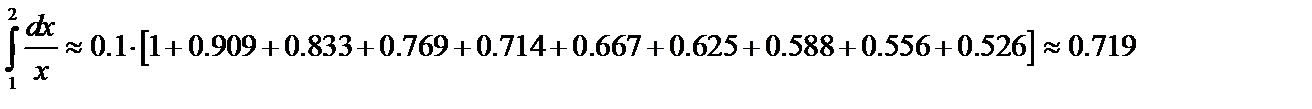
Пример 2. Найти приближенное значение интеграла 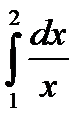, вычисленное по формуле трапеций при n=10 с точностью до 0,0001:
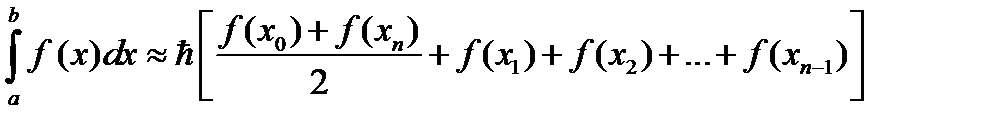
Решение. По условию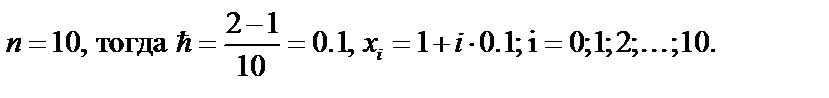 
Найдём значения аргументов х i и соответствующие значения функции f( xi) c шагом 0,1:
|
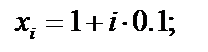
| f( xi)= 1 ∕х i |
|
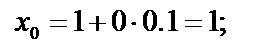
| f ( x0 )= 1 ∕х 0 = 1 ∕ 1=1 |
|
| f ( x 1 )= 1 ∕х1=1 ∕1. 1 ≈ 0.909 1 |
|
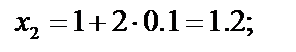
| f ( x2 )= 1 ∕х 2 =1 ∕1 .2 ≈ 0.833 3 |
|
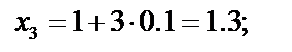
| f ( x3 )= 1 ∕х 3 =1 ∕1 .3 ≈ 0.769 2 |
|
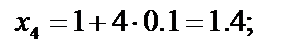
| f ( x4 )= 1 ∕х 4 = 1 ∕ 1.4 ≈ 0.714 2 |
|
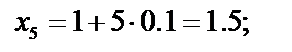
| f ( x5 )= 1 ∕х 5 = 1 ∕ 1.5 ≈ 0.6667 |
|
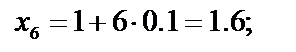
| f ( x6 )= 1 ∕х 6 = 1 ∕ 1.6 ≈ 0.6250 |
|
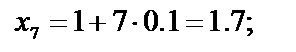
| f ( x7 )= 1 ∕х 7 = 1 ∕ 1.7 ≈ 0.5882 |
|
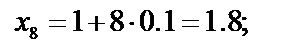
| f ( x8 )= 1 ∕х 8 = 1 ∕ 1.8 ≈ 0.5556 |
|
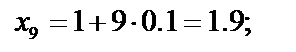
| f ( x9 )= 1 ∕х 9 = 1 ∕ 1.9 ≈ 0.5263 |
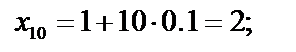
| f ( x 10 )= 1 ∕х 10 =1 ∕2 = 0.5 |
Подставим найденные значения в формулу трапеций и вычислим приближённое значение интеграла с точностью до 0,0001:
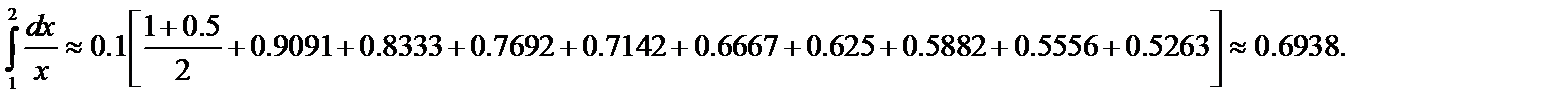
Пример 3. Найти приближенное значение интеграла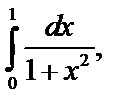 
вычисленное по формуле Симпсона при n=2 с точностью до 0,0001:
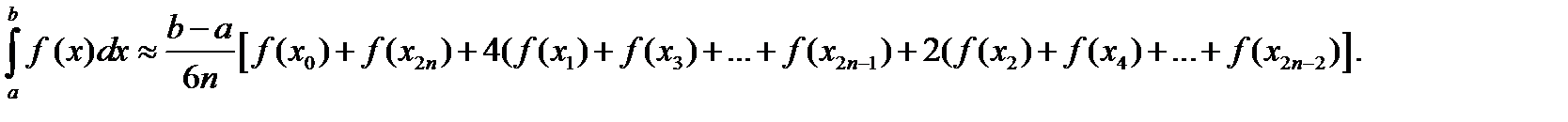
Решение. По условию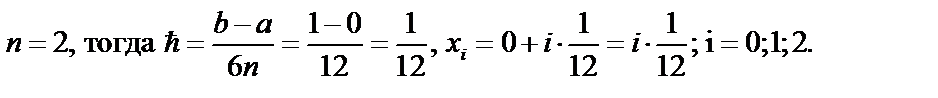 
Найдём значения аргументов х i и соответствующие значения функции f( xi) c шагом 1 ∕ 12:
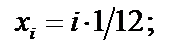
| f( xi)= 1 ∕ 1 +х 2 i |
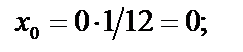
| f ( x0 )= 1 ∕ 1 + х 2 0 = 1 ∕ 1=1 |
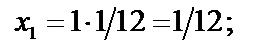
| f ( x 1 )= 1 ∕ 1 + х 2 1 =1 ∕1 45 ∕ 144 ≈ 0.9931 |
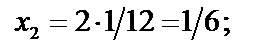
| f ( x 2 )= 1 ∕ 1+ х 2 2 =1 ∕ 37 ∕ 36 ≈ 0. 9730 |
| f ( x3 )= 1 ∕ 1+ х 2 3 =1 ∕ 17 ∕ 16 ≈ 0. 9412 |
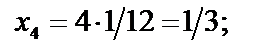
| f ( x4 )= 1 ∕ 1+ х 2 4 =1 ∕ 10 ∕ 9 ≈ 0. 9 |
Подставим найденные значения в формулу Симпсона и вычислим приближённое значение интеграла с точностью до 0,0001:
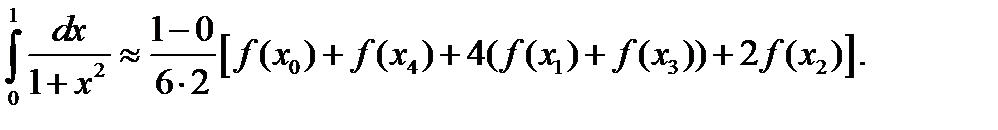
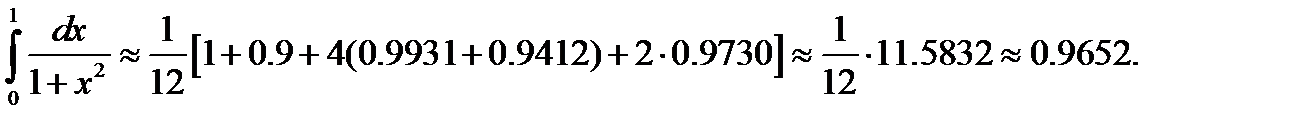
Задания для самостоятельного выполнения:
1. Найти приближённые значения интегралов по формуле прямоугольников.
2. Вычислить приближённое значение интеграла по формуле трапеций с точностью до 0,0001.
3. Найти приближённое значение интеграла по формуле Симпсона с точностью до 0,001.
1. а)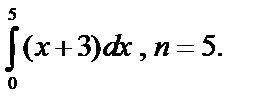 
б) 
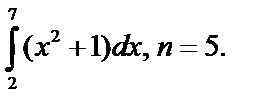в)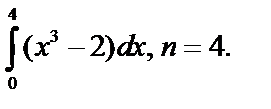 
2. 
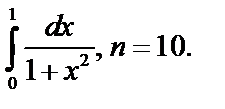
3. 
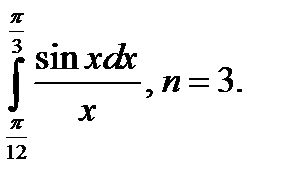
Вопросы для самоконтроля:
1. Как найти приближённое значение интеграла по формуле прямоугольников?
2. Запишите формулу трапеций для приближённого вычисления определённого интеграла.
3. Формула Симпсона (формула параболических трапеций)?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 19
ОТНОШЕНИЯ МНОЖЕСТВ
Цель:
- сформировать навыки задания множеств;
- развить умения устанавливать отношения множеств;
- закрепить знания о свойствах отношений;
Материально – техническое обеспечение: методические указания по выполнению работы, чертёжные инструменты;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
На конкретных примерах покажем алгоритм выполнения операций над множествами, способы их заданий, установим отношения множеств.
Пример 1. Найти все подмножества множества А = { 1; 2; 3 }.
Решение: Данное множество состоит из 3-х элементов, n=3, значит, оно имеет 23 = 8 подмножеств. Тогда подмножествами данного множества являются следующие множества:
{ 1 }, { 2 }, { 3 }, { 1; 2 }, { 1; 3 }, { 2; 3 }, { 1; 2; 3 }, {Ø}.
Пример 2. Определить все равные множеству А = {2,4,6,8} множества.
Решение: Множества называют равными, если они состоят из одних и тех же элементов, причем порядок их расстановки не имеет значения. Множество А состоит из 4-ёх элементов, значит, число перестановок его элементов равно 4!= 1*2*3*4=24. Таким образом, множество А имеет 24 равных множества, включая его само: А1={2,4,6,8}, А2={2,4,8,6}, А3={2,6,4,8}, А4={2,6,8,4}, А5={2,8,4,6}, А6={2,8,6,4}, А7={4,2,6,8}, А8={4,2,8,6}, А9={4,6,8,2}, А10={4,6,2,8}, А11={4,8,6,2}, А12={4,8,2,6}, А13={6,4,2,8}, А14={6,4,8,2}, А15={6,2,4,8}, А16={6,2,8,4}, А17={6,8,4,2}, А18={6,8,2,4}, А19={8,6,4,2}, А20={8,6,2,4}, А21={8,2,6,4}, А22={8,2,4,6}, А23={8,4,6,2}, А24={8,4,2,6}.
Пример 3. Указать характеристическое свойство элементов множества
А ={12,22,32,42,52,62,72,82,92}.
Решение: Характеристическое свойство – свойство, которым обладает каждый элемент данного множества и не обладает ни один элемент, ему не принадлежащий. Все перечисленные элементы являются натуральными, двузначными и оканчиваются цифрой 2.
Задания для самостоятельного выполнения:
1) Найти все подмножества данного множества;
2) Определить все равные данному множеству множества;
3) Укажите характеристическое свойство элементов данного множества;
Вариант 1.
1. А = { 1; 3; 7; 9 }.
2. А = { -3; -4; -5; -6 }.
3. А = { 11; 13; 15; 17;19 }.
Вариант 2.
1. А = { 3; 4; 5; 7 }.
2. А = { 3; 4; 6; 8 }.
3. А = { 21; 23; 25; 27;29 }.
Вариант 3.
1. А = { -1; -2; -3; -4 }.
2. А ={ 5; 1; 3; 6 }.
3. А ={ 18; 15; 12 }.
Вариант 4.
1. А = { -1; 0; 1; 2 }.
2. А = { 1; 2; 5; 8 }.
3. А ={ 10; 15; 20;25;30;35;40;45;50;55;60;65;70;75;80;85;90;95 }.
Вариант 5.
1. А = { 0; 1; 2; 6 }.
2. А = { 3; 1; 7; 9 }.
3. А = { 78; 76; 74; 72;70 }.
Вариант 6.
1. А = { 2; 6; 7; 8 }.
2. А = { 5; 2; 4; 3 }.
3. А = { 31; 33; 35; 37;39 }.
Вариант 7.
1. А = { 4; 6; 7; 9 }.
2. А = { 7; 9; 3; 5 }.
3. А = { 98; 96; 94; 92; 90 }.
Вариант 8.
1. А = { 1; 4; 5; 7; 9 }.
2. А = { 3; 5; 7; 9 }.
3. А ={ 20; 22; 24; 26; 28 }.
Вариант 9.
1. А = { 7; 8; 9; 3; 5 }.
2. А = { 4; 6; 7; 9 }.
3. А = { 11; 22; 33; 44; 55; 66; 77; 88; 99 }.
Вариант 10.
1. А = { 5; 2; 4; 3; 7 }.
2. А = { 2; 6; 7; 8 }.
3. А = { 41; 43; 45;47;49 }.
Вариант 11.
1. А = { 3; 1; 7; 9; 5 }.
2. А = { 0; 1; 2; 6 }.
3. А ={ 60; 62;64; 66; 68 }.
Вариант 12.
1. А = { 7; 2; 9; 5; 1 }.
2. А = { -1; 0; 1; 2 }.
3. А ={ 27; 24; 21 }.
Вариант 13.
1. А = { 5; 1; 3; 6; 8 }.
2. А = { -1; -2; -3; -4 }.
3. А ={ 30; 32; 34; 36; 38 }.
Вариант 14.
1. А = { 2; 3; 4; 6; 9 }.
2. А = { 1; 2; 3; 4 }.
3. А = { 111; 222; 333; 444; 555; 666; 777; 888; 999 }.
Вариант 15.
1. А = { 6; 7; 1; 1/2; 1/3 }.
2. А = { 3; 4; 5; 7 }.
3. А = { 88; 86; 84; 82; 80 }.
Вопросы для самоконтроля:
1. Перечислите способы задания множеств.
2. Какие множества называют равными?
3. Что называют характеристическим свойством множества?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 20
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Цель:
- сформировать навыки выполнения операций над множествами;
- развить умения построения кругов Эйлера - Венна;
- закрепить знания об отношениях множеств;
Материально – техническое обеспечение: методические указания по выполнению работы, чертёжные инструменты;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
На конкретных примерах покажем выполнение операций над множествами, графическое изображение множеств с помощью диаграмм Эйлера.
Пример 2. Найдите:
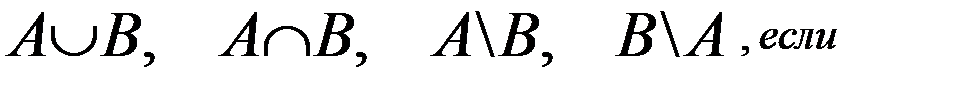
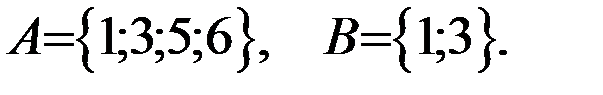
Решение:
Находим:
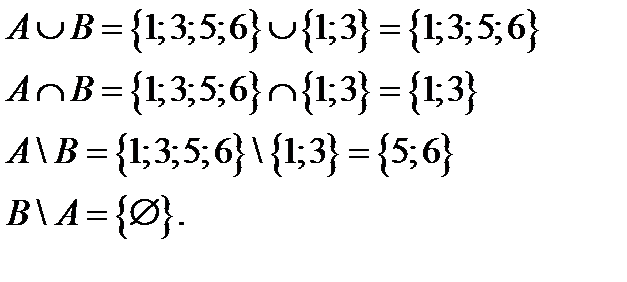
Пример 3. Найти декартово произведение множеств А={1,2,3} и В = {3,5}.
Решение:
Декартовым произведением множеств А и В называется множество всех пар, образованных из элементов обоих множеств, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В.
А × В= {(1;3),(1;5),(2;3),(2;5),(3;3),(3;5)}
| А*В | 3 | 5 |
| 1 | (1;3) | (1,5) |
| 2 | (2,3) | (2, 5 ) |
| 3 | (3,3) | (3, 5 ) |
Задания для самостоятельного выполнения:
I. Изобразите на диаграммах Эйлера – Венна данные множества.
II. Выполните операции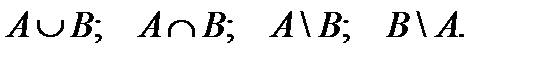 
III. Найдите декартово произведение множеств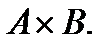 
Вариант 1.
1. 
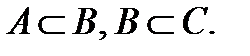
2. А = { 3; 4; 5;7 }, B = { 3; 5; 6 }.
3. А = { 2; 3; 5; 6 }, B = { 1; 2; 3 }.
Вариант 2.
1. 
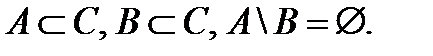
2. А={ 0; 1; 7; 8 }, B ={ -7; 0; 6; 9 }.
3. А = { 1; 5; 7; 9 }, B = { 4; 5; 7 }.
Вариант 3.
1. 
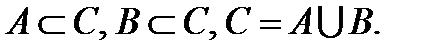
2. А={ 1; 3; 5; 7 }, B = { 2; 4; 6; 8 }.
3. А = { 2; 4; 6; 9 }, B = { 5; 7; 8 }.
Вариант 4.
1. 
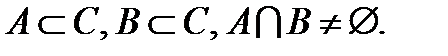
2. А={ 1; 2; 3 }, B ={ -1; 0; 2; 3 }.
3. А = { 6; 3; 4; 8 }, B = { 3; 2; 1 }.
Вариант 5.
1. 
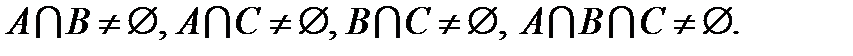
2. А={ 1; 2; 3 }, B ={ 0; 1; 2; 3; 5 }.
3. А = { 5; 6; 8; 9 }, B = { 3; 1; 4 }.
Вариант 6.
1. 
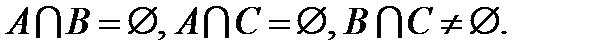
2. А={ -3; -1; 0; 1}, B = {2; -1; -2 }.
3. А = { 0; 1 }, B = { -1; 0; 1; 2 }.
Вариант 7.
1. 
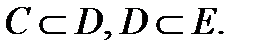
2. А={ -2; -1; 0; 1; 2 }, B ={ -1; 0; 4 }.
3. А = { 6; 7; 9 }, B = { 1; 2; 5; 7 }.
Вариант 8.
1. 
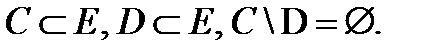
2. А={ 0; 1; 2; 3; 7 }, B ={ 5; 3; 1; 0 }.
3. А = { 3; 6; 8 }, B = { 6; 3; 2; 1 }.
Вариант 9.
1. 
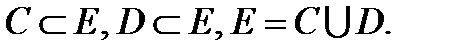
2. А={ 1; 2; 3; 7 }, B ={0; 1; 3; 4 }.
3. А = { 7; 8; 2; 1 }, B = { 1; 2; 5; 7 }.
Вариант 10.
1. 
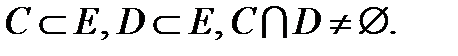
2. А={ 5; 7; 8 }, B ={ 8; 9 }.
3. А = { -2; -1; 0; 6 }, B = { 2; 3; 6 }.
Вариант 11.
1. 
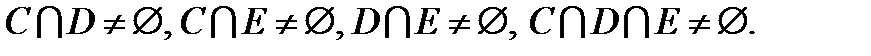
2. А={ 5; 6; 7; 8; 9 }, B ={6; 8; 9 }.
3. А = { -6; 1; 2; 7; 8 }, B = { 3; 6; -4 }.
Вариант 12.
1. 
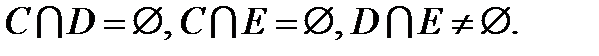
2. А={ 1; 2; 3; 4 }, B={ 0; 1/2; 1}.
3. А = { 4; 8; 2; 7 }, B = { 1/3; 5; 1; 8 }.
Вариант 13.
1. 
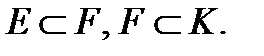
2. А={ 3; 4; 5; 7 }, В ={0; 1; 4; 7}
3. А = { 2; 7; 0; 8; 9 }, B = { 5; 1; 2; 3 }.
Вариант 14.
1. 
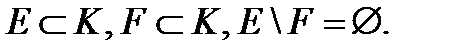
2. А={ 1/3; 4; 7; 9}, B ={ 6; 7; 9 }.
3. А = { -1; 0; 1; 2 }, B = { 5; 3; 4 }.
Вариант 15.
1. 
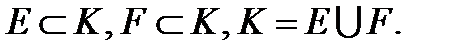
2. А={1/6; 3; 4 }, B= {1/6; 2; 3; 4}.
3. А = { 0; 1; 2; 5 }, B = { 3; 4; 6; 7 }.
Вопросы для самоконтроля:
1. Перечислите основные операции над множествами.
2. Что изображают диаграммой Эйлера – Венна?
3. Дайте определение декартовому произведению множеств.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 21
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Цель:
- сформировать навыки решения комбинаторных задач;
- развить умения вычисления комбинаторных соединений;
- закрепить знания об элементах комбинаторики;
Материально – техническое обеспечение: методические указания по выполнению работы;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения: На основе конкретных примеров покажем способы вычисления перестановок, размещений, сочетаний, факториала.
Пример1. Сколькими способами можно составить дозор из трех солдат и одного офицера, если имеется 80 солдат и 3 офицера?
Решение:
Используем формулу вычисления: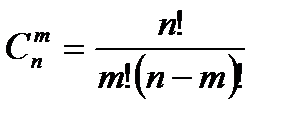 
.
Солдат в дозор можно выбрать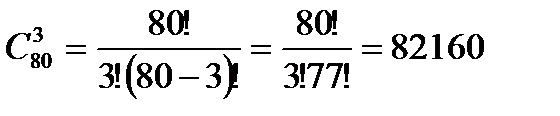 
способами, а офицеров 
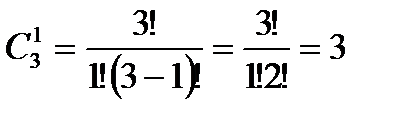способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется 246480 способов.
Пример 2. Сколько двухзначных комбинаций можно составить из четырех букв А, В, С, D, при условии, что ни одна из них не повторяется?
Решение:
Так как двухзначные комбинации отличаются друг от друга или самими буквами, или их порядком, то искомое количество равно числу размещений из четырех элементов по два.
Число размещений вычислим по формуле:
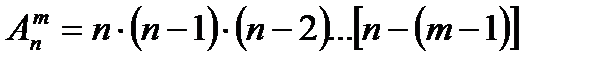
Итак,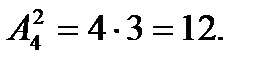 
Всего имеется 12 различных комбинаций.
Пример 3.
Сколькими способами можно расставить 6 различных книг на полке, чтобы определенные 4 книги стояли рядом?
Решение:
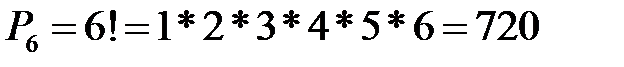Если обозначить 4 определенные книги как одно целое, то получается 6 книг, которые можно переставлять способами.
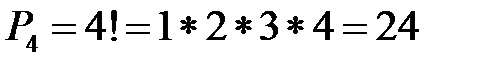4 определенные книги можно переставлять способами.
Тогда всего перестановок по правилу умножения будет
Задания для самостоятельного выполнения:
1-2. Решить комбинаторные задачи.
3. Найти корни уравнения.
Вариант 1.
1. Сколько двузначных чисел можно составить из цифр 1, 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых цифр?
2. Из 6 открыток надо выбрать 3. Сколькими способами это можно сделать?
3. Решить уравнение: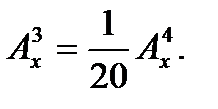 
Вариант 2.
1. Сколькими способами могут разместиться 5 человек за столом?
2. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов?
3. Решить уравнение: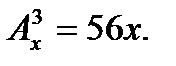 
Вариант 3.
1. Сколько различных пятизначных чисел можно составить из цифр 0, 1, 3, 5, 7 так, чтобы в каждом числе не было одинаковых чисел?
2. Из 10 кандидатов нужно выбрать 3 человека на конференцию. Сколькими различными способами это можно сделать?
3. Решить уравнение: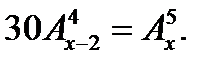 
Вариант 4.
1. Бригадир должен отправить на работу бригаду из трех человек. Сколько таких бригад можно составить из 8 человек?
2. На собрании должны выступать 5 человек (А, В, С, Д, Е). Сколькими способами их можно разместить в списке выступающих, если А должен выступать первым?
3. Решить уравнение: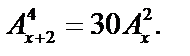 
Вариант 5.
1. Сколькими способами можно расставить на полке 6 книг?
2. Сколькими способами можно выбрать гласную и согласную буквы из слова «журнал»?
3. Решить уравнение: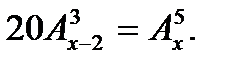 
Вариант 6.
1. Сколькими способами можно составить список из 6 человек?
2. Сколькими способами собрание, состоящее из 18 человек, может из своего состава выбрать председателя и секретаря?
3. Решить уравнение: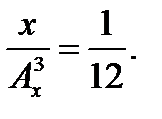 
Вариант 7.
1. Среди перестановок из цифр 1, 2, 3, 4, 5 сколько таких, которые не начинаются цифрами 3 и 5?
2. Сколькими способами можно выбрать различные краски из имеющихся пяти?
3. Решить уравнение: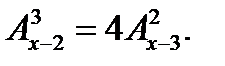 
Вариант 8.
1. Сколькими различных трехзначных чисел, не содержащих одинаковых цифр, можно составить из цифр 1, 2, 3, 4 , 5, 6, 7, 8, 9?
2. При встрече 16 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
3. Решить уравнение: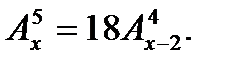 
Вариант 9.
1. Имеется 8 пар перчаток различных размеров. Сколькими способами можно выбрать из них одну перчатку на левую руку и одну на правую руку так, чтобы эти перчатки были различных размеров?
2. Сколькими способами можно разместить в четырехместной каюте четырех человек?
3. Решить уравнение: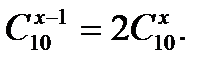 
Вариант 10.
1. Сколько различных двузначных чисел можно образовать из цифр 1, 2, 3, 4 при условии, что в каждом числе нет одинаковых цифр?
2. В местком избрано 11 человек. Из них надо выбрать председателя, заместителя председателя, секретаря. Сколькими способами это можно сделать?
3. Решить уравнение: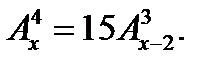 
Вариант 11.
1. Сколько различных двузначных чисел можно составить из цифр 1, 2, 5, 7?
2. Студенты данной группы изучают 8 учебных предметов. Если расписание занятий каждого дня включается по 4 предмета, то сколькими способами могут быть распределены предметы в день?
3. Решить уравнение: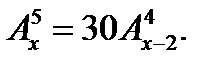 
Вариант 12.
1. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?
2. Сколькими способами можно разложить семь монет различного достоинства в два кармана?
3. Решить уравнение: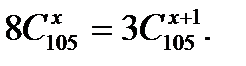 
Вариант 13.
1. Сколько различных диагоналей можно провести в выпуклом десятиугольнике?
2. Пять девушек и три юноши играют в баскетбол. Сколькими способами они могут быть разбиться на две команды по четыре игрока, если в каждой команде должно быть не менее одного юноши?
3. Решить уравнение: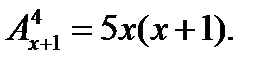 
Вариант 14.
1. Сколько может быть случаев при выборе двух карандашей и трех ручек из пяти различных карандашей и пяти различных ручек?
2. Укротителю диких зверей предстоит вывести на арену цирка одного за другим пять львов и четыре тигра. Сколькими способами он может это сделать, причем так, чтобы никакие два тигра не шли друг за другом?
3. Решить уравнение: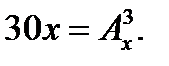 
Вариант 15.
1. Сколько двузначных чисел можно составить из цифр 1, 3, 5, 8, 9 так, чтобы в каждом числе не было одинаковых чисел?
2. Из цифр 0, 1, 2 , 3 составлены все возможные четырехзначные числа так, что в каждом числе нет одинаковых цифр. Сколько получилось чисел?
3. Решить уравнение: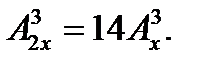 
Вопросы для самоконтроля:
1. Что называется n – факториалом?
2. Перечислите основные виды комбинаторных соединений.
3. Запишите формулы вычислений перестановок, размещений, сочетаний.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 22
ВЕРОЯТНОСТЬ СОБЫТИЯ
Цель:
- сформировать навыки решения вероятностных задач;
- развить умения вычисления вероятностей совместных и несовместных, независимых событий;
- закрепить знания о теоремах сложения и умножения вероятностей.
Материально – техническое обеспечение: методические указания по выполнению работы;
Время выполнения: 2 академических часа;
Ход занятия:
1. Изучить краткие теоретические сведения;
2. Выполнить задания;
3. Сделать вывод по работе;
4. Подготовить защиту работы по контрольным вопросам.
Краткие теоретические сведения:
На основе конкретных примеров покажем способы вычисления вероятностей события.
Пример 1.
В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение.
Общее число различных исходов есть n=1000. Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле P(A)=m/n , получим Р(А)=200/1000=1/5=0,2.
Пример 2.
Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Решение.
Обозначим событие, состоящее в появлении черного шара, через А. Общее число случаев n=5+3=8. Число случаев m, благоприятствующих появлению события А, равно 3. По формуле P(A)=m/n получим Р(А)=m/n=3/8=0,375.
Пример 3.
Из урны в которой находится 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными?
Решение.
Обозначим событие, состоящее в проявлении черного шара, через А. Общее число возможных случаев n равно числу сочетаний из 20 элементов (12+8) по два: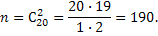 
Число случаев m, благоприятствующих событию А, составляет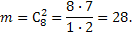 
По формуле P(A)=m/n находим вероятность появления двух черных шаров: Р(А)=m/n=28/190=14/95=0,147.
Пример 4.
Найти вероятность того, что наудачу взятое двузначное число окажется кратным либо 3, либо 5, либо тому и другому одновременно.
Решение.
Пусть А- событие, состоящее в том, что наудачу взятое число кратно 3, а В- в том, что оно кратно 5. Найдем Р(А+В). Так как А и В совместные события, то воспользуемся формулой Р(А+В)=Р(А)+Р(В)-Р(АВ).
Всего имеется 90 двузначных чисел: 10,11,…,98,99. Из них 30 являются кратными 3 (благоприятствуют наступлению события А); 18- кратными 5 (благоприятствуют наступлению события В) и 6- кратными одновременно 3 и 5 (благоприятствуют наступлению события АВ). Таким образом, Р(А)=30/90=1/3, Р(В)=18/90=1/5, Р(АВ)=6/90=1/15, т.е. Р(А+В)=1/3+1/5-1/15=7/15=0,467.
Пример 5.
В одной урне находится 4 белых и 8 черных шаров, в другой – 3 белых и 9 черных. Из каждой урны вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
Решение.
Пусть А - появление белого шара из первой урны, а В - появление белого шара из второй урны. Очевидно, что события А и В независимы. Найдем Р(А) = 4/12=1/3, Р(В) = 3/12=1/4.
По формуле получим Р(АВ)=Р(А)*Р(В)=(1/3)*(1/4)=1/12=0,083.
Задания для самостоятельного выполнения:
Найти вероятности данных событий.
Вариант 1.
1. В лотерее из 50 билетов 8 выигрышных. Какова вероятность того, что среди пяти наугад выбранных билетов два окажутся выигрышными?
2. На карточках разрезной азбуки написаны 32 буквы русского алфавита. 4 карточки вынимают наугад одну за другой и укладывают на стол в порядке появления. Какова вероятность того, что получится слово “ Югра”?
Вариант 2.
1. Из шести одинаковых карточек разрезной азбуки: “а”, ”е”, ”м”,”н”,”о”, ”р” наудачу выбирают четыре карточки и складывают их в ряд в порядке их извлечения. Какова вероятность при этом получить слово “море”?
2. В партии из 15 деталей имеется 9 стандартных. Найдите вероятность того, что среди семи взятых наугад деталей 5 стандартных?
Вариант 3.
1. На шести одинаковых карточках написаны буквы “а”, ”в”, ”к”,”м”, ”о”, ”с” . Карточки перемешивают и раскладывают наудачу в ряд. Какова вероятность того, чтобы получилось слово “Москва”?
2. В партии из 10 деталей имеется 8 стандартных. Найдите вероятность того, что среди двух взятых наугад деталей одна бракованная?
Вариант 4.
1. Из урны, содержащей 5 шаров с цифрами 1, 2, 3,4,5 извлекают наудачу все шары один за другим. Какова вероятность того, что номера извлеченных шаров идут в порядке возрастания?
2. Экзаменационные билеты пронумерованы числами от 1 до 35. Какова вероятность того, что номер выбранного билета нечётный?
Вариант 5.
1. В партии из 100 деталей 5 % бракованных. Какова вероятность того, что наугад выбранная деталь окажется стандартной?
2. Трехтомное собрание сочинений М.Ю. Лермонтова расположено на полке в случайном порядке. Какова вероятность того, что тома стоят по порядку номеров?
Вариант 6.
1. Из полного набора домино наудачу извлекают одну кость. Какова вероятность того, что число очков на ней четно?
2. Из 50 электролампочек имеется 4 бракованных. Какова вероятность того, что две взятые наугад лампы окажутся бракованными?
Вариант 7.
1. Из 60 экзаменационных вопросов учащийся подготовил 50. На экзамене он должен ответить на два вопроса. Какова вероятность того, что учащийся ответит на оба вопроса?
2. В книжном магазине на полке лежит 20 книг, причем 10 книг стоят по 20 руб. каждая, 3 книги - по 40 руб. и 7 книг - по 10руб. Найти вероятность того, что взятые наугад две книги стоят 50 руб.?
Вариант 8.
1. Из 10 билетов лотереи выигрышными являются два. Какова вероятность того, что среди взятых наудачу пяти билетов два выигрышных?
2. На шести одинаковых карточках написаны буквы “а”, ”в”, ”к”,”м”, ”о”, ”с” . Карточки перемешивают и раскладывают наудачу в ряд. Какова вероятность того, чтобы получилось слово “Москва”?
Вариант 9.
1. В урне 100 шаров, помеченных номерами 1,2,3,…100. Из урны наугад выбирают один шар. Какова вероятность того, что номер вынутого шара содержит цифру 5?
2. Задания программированной контрольной работы пронумерованы всеми двухзначными числами. Какова вероятность того, что номер наугад выбранного задания состоит из одинаковых цифр?
Вариант 10.
1. В урне 6 белых и 9 черных шаров. Из урны вынимают одновременно два шара. Какова вероятность того, что оба шара окажутся черными?
2. На карточках разрезной азбуки написаны 32 буквы русского алфавита. Шесть карточек вынимают наугад одну за другой и укладывают на стол в порядке появления. Какова вероятность того, что получится слово “ призма”?
Вариант 11.
1. В партии из 8 деталей имеется 6 стандартных. Какова вероятность того, что среди пяти взятых наугад деталей ровно 3 стандартных?
2. Четырехтомное собрание сочинений А.С. Пушкина расположено на полке в случайном порядке. Какова вероятность того, что тома стоят по порядку номеров?
Вариант 12.
1. Восемь различных книг расставляют наугад на одной полке. Какова вероятность того, что две определенные книги окажутся поставленными рядом?
2. Экзаменационные билеты пронумерованы числами от 1 до 35. Какова вероятность того, что номер выбранного билета чётный?
Вариант 13.
1. В урне 7 белых и 5 черных шаров. Из урны наугад вынимают два шара. Найдите вероятность того, что два шара белые.
2. В книжном магазине на полке лежит 20 книг, причем 10 книг стоят по 20 руб. каждая, 3 книги - по 40 руб. и 7 книг - по 10руб. Найти вероятность того, что взятые наугад две книги стоят 30 руб.?
Вариант 14.
1. В урне 8 красных и 5 синих шаров. Из урны наугад вынимают два шара. Найдите вероятность того, что они разного цвета.
2. Брошена игральная кость. Какова вероятность того, что выпадет четное число очков?
Вариант 15.
1. Десять различных книг расставляют наугад на одной полке. Найдите вероятность того, что три определенные книги окажутся поставленными рядом.
2. В партии из 12 деталей имеется 9 стандартных. Найдите вероятность того, что среди семи взятых наугад деталей 6 стандартных?
Вопросы самоконтроля:
1. Что называется вероятностью события?
2. Сформулируте теоремы сложения и умножения вероятностей.
3. Приведите примеры совместных и несовместных, независимых событий;
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 23
История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!