Поглощение электромагнитных волн из-за столкновений между частицами. В элементарной теории это поглощение по-прежнему учитывается введением члена - me n eff 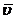 в правую часть уравнения движения электрона (4.3). То есть теперь мы имеем:
в правую часть уравнения движения электрона (4.3). То есть теперь мы имеем:
 .
.
Введем обозначения:

 .
.
Тогда уравнение движение можно записать в виде:
U 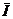 -i[
-i[ 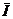 ,
,  ]+X
]+X  =0.
=0.
Из уравнений Максвелла имеем ( 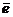 - единичный орт вдоль волнового вектора):
- единичный орт вдоль волнового вектора):
rot  =i[
=i[ 
 ]=i w n/c[
]=i w n/c[ 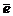
 ]=i w /c
]=i w /c 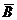 или
или  n[
n[ 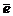
 ],
],
а также:
rot 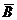 =-i w /c
=-i w /c  +
+  или n[
или n[ 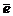
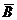 ]+
]+  +
+ 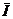 =0.
=0.
Таким образом, имеем систему уравнений:
U 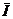 -i[
-i[ 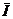 ,
,  ]+X
]+X  =0
=0
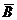 =n[
=n[ 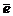
 ]
]
n[ 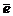
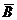 ]+
]+  +
+ 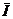 =0.
=0.
Подставим второе уравнение в третье и раскроем в результате двойное векторное произведение. В итоге имеем систему из двух уравнений:
U 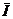 -i[
-i[ 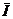 ,
,  ]+X
]+X  =0
=0
n2( 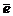
 )
) 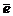 - n2
- n2  +
+  +
+ 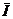 =0.
=0.
Из второго уравнения получим 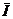 и подставим в первое уравнение.
и подставим в первое уравнение.
U(n2-1)  -n2U(
-n2U( 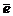
 )
) 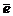 -i(n2-1)[
-i(n2-1)[ 
 ]+in2(
]+in2( 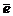
 )[
)[ 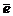
 ]+X
]+X  =0,
=0,
или:
(U(n2-1)+X)  -n2U(
-n2U( 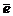
 )
) 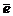 -i(n2-1)[
-i(n2-1)[ 
 ]+in2(
]+in2( 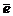
 )[
)[ 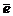
 ] =0. (5.1)
] =0. (5.1)
Направим ось z по вектору 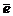 . Вектор
. Вектор  расположим в плоскости zx. Тогда
расположим в плоскости zx. Тогда  =Yt
=Yt 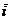 + Ye
+ Ye 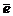 .
.
Используем далее соотношения:
[ 
 ]=
]= 
и
[ 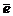
 ]=[
]=[ 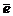 , Yt
, Yt 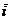 ]=Yt
]=Yt 
Спроектируем уравнение (5.1) на координатные оси:
(U(n2-1)+X)Ex-i(n2-1)YeEy
(U(n2-1)+X)Ey-i(n2-1)(YtEz-YeEx)+in2YtEz=0
(U(n2-1)+X)Ez- n2UEz+i(n2-1)YtEy=0.
Определитель этой системы равен:
 =
=
=(n2-1)2U2(X-U)+2(n2-1)UX(X-U)+X2(X-U)+
+ (n2-1)2UYt2+(n2-1)XYt2+(n2-1)2Ye2(U-X)=0,
или:
D=(n2-1)2(U2(X-U)+ UYt2+ Ye2(U-X))+
+(n2-1)(2UX(X-U)+ XYt2)+ X2(X-U)=0.
Тогда, используя соотношение
x2=1+ 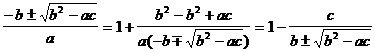 , получаем формулу Аппельтона-Хартри:
, получаем формулу Аппельтона-Хартри:
 .
.
В квазипродольном приближении можно положить Yt=0, тогда:
 ,
,
где n± - действительный показатель преломления, а h± - показатель поглощения. Учитывая малость Z, отсюда получим:
 ,
,  . (5.2)
. (5.2)
Здесь  .
.
В достаточно разреженном слое плазмы ( v << 1) со слабым магнитным полем (  ) и в широком интервале углов a , где реализуется случай квазипродольного распространения, оптическая толщина:
) и в широком интервале углов a , где реализуется случай квазипродольного распространения, оптическая толщина:
 . (5.3)
. (5.3)
Здесь  = BT –3/2 N 2 L , где L - толщина слоя. При написании формулы (5.3) учтено, что:
= BT –3/2 N 2 L , где L - толщина слоя. При написании формулы (5.3) учтено, что:
 ,
,
и величина h1,2=h± получена путем разложения в ряд по степеням 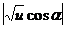 выражения (5.2). Яркостная температура теплового тормозного излучения из слоя Т b1,2= Т(1 -
выражения (5.2). Яркостная температура теплового тормозного излучения из слоя Т b1,2= Т(1 - 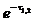 ) и на частотах w 2 << w cr 2 будет равна Т для обоих типов волн. Степень поляризации излучения на этих частотах равна нулю. В области w 2 >> w cr 2 слой становится оптически тонким, Т b1,2= T t1,2- Поскольку t1> t2(см. (5.3)), отсюда заключаем, что наложение магнитного поля на плазму увеличивает интенсивность тормозного излучения на необыкновенной волне, снижая одновременно излучение обыкновенной компоненты. Суммарная интенсивность I w µ Tb 1 + Tb 2 при этом не меняется (точнее, она возрастает в более высоком приближении по степеням
) и на частотах w 2 << w cr 2 будет равна Т для обоих типов волн. Степень поляризации излучения на этих частотах равна нулю. В области w 2 >> w cr 2 слой становится оптически тонким, Т b1,2= T t1,2- Поскольку t1> t2(см. (5.3)), отсюда заключаем, что наложение магнитного поля на плазму увеличивает интенсивность тормозного излучения на необыкновенной волне, снижая одновременно излучение обыкновенной компоненты. Суммарная интенсивность I w µ Tb 1 + Tb 2 при этом не меняется (точнее, она возрастает в более высоком приближении по степеням 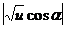 ). Поэтому частотный спектр излучения 1 w ( w ) отличается от представленного на графике рис.4.2. Степень круговой поляризации излучения, выходящего за пределы источника, равна:
). Поэтому частотный спектр излучения 1 w ( w ) отличается от представленного на графике рис.4.2. Степень круговой поляризации излучения, выходящего за пределы источника, равна:
 .
.
Эта формула позволяет оценить продольную компоненту магнитного поля Bo½cos a½ в источнике теплового тормозного излучения по измеренной степени круговой поляризации. Измерения при этом должны производиться в той области частотного спектра, где источник – оптически тонкий, то есть на частотах w 2 >> w cr 2 .
Глава 6. Перенос излучения
Уравнение переноса в изотропной плазме
Для определения интенсивности излучения источника при знании физических условий в нем необходимо решать задачу переноса излучения в среде источника.
Интенсивность излучения в элементарном объеме изменяется за счет поглощенной  и излученной энергии
и излученной энергии  :
:
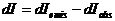 .
.
Доля поглощенной энергии пропорциональна коэффициенту поглощения среды 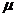 и длине пройденного пути
и длине пройденного пути  :
:
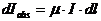 .
.
Для нахождения  воспользуемся законом Кирхгофа, согласно которому отношение коэффициента излучения
воспользуемся законом Кирхгофа, согласно которому отношение коэффициента излучения  к
к 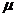 есть величина, равная для теплового излучения интенсивности излучения «абсолютно черного» тела
есть величина, равная для теплового излучения интенсивности излучения «абсолютно черного» тела  . Величина
. Величина  определяется формулой Планка:
определяется формулой Планка:
 .
.
В радиодиапазоне 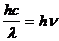 <<
<< 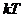 и формула Планка переходит в формулу Релея-Джинса:
и формула Планка переходит в формулу Релея-Джинса:
 .
.
Итак: 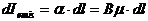 .
.
Введем понятие оптической глубины. Если излучение идет к нам, то оптическую глубину удобнее измерять от наблюдателя. Тогда определим оптическую глубину 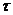 как
как

Тогда  . Следовательно:
. Следовательно:
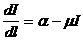 ,
,
или:
 . (6.1)
. (6.1)
Затем получим: (  )
) 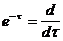 (
(  )
) 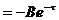 .
.
Интегрируя обе части этого выражения от 0 до  , находим:
, находим:
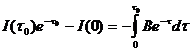 ,
,
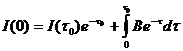 .
.
Если 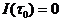 и
и  << 1, то
<< 1, то 
 или в температурах
или в температурах  .
.
Поскольку aw не связана с интенсивностью излучения I w, она характеризует спонтанные процессы, не зависящие от наличия или отсутствия излучения вдоль данного луча. Наоборот, член m j I w определяет те индуцированные (вынужденные) процессы излучения и поглощения, которые происходят лишь под действием излучения, переносимого вдоль этого луча, и исчезают при I w -> 0. Как aw, так и m j, могут зависеть от интенсивности излучения вдоль других лучей (или от величины интенсивности вдоль данного луча, но переносимой в противоположном направлении, или имеющей другую частоту). В этом случае речь идет об учете в уравнении переноса (6.1) процессов рассеяния излучения.
| Рис. 6.1. К учету рефракции.
|
Уравнение переноса (6.1) справедливо лишь в однородной среде. При переходе к случаю неоднородной плазмы в уравнении переноса следует учесть то обстоятельство, что интенсивность излучения не сохраняется вдоль луча даже при a w = 0 и m = 0. Это связано, в конечном счете, с изменением телесного угла dW, в котором распространяется излучение, вследствие рефракции в среде с показателем преломления nj ( 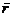 ). Будем предполагать, что изотропная плазма - плоскослоистая, т. е. ее показатель преломления nj зависит только от одной декартовой координаты z . Учет рефракции в этом случае значительно упрощается.
). Будем предполагать, что изотропная плазма - плоскослоистая, т. е. ее показатель преломления nj зависит только от одной декартовой координаты z . Учет рефракции в этом случае значительно упрощается.
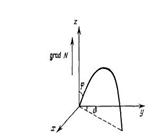
Введем в плоскослоистой среде систему координат х, у, z , направив ось z вдоль grad N. Рассмотрим луч, расположенный в плоскости, проходящей через ось z , и составляющий с плоскостью у z угол J (рис. 6.1).
Уравнение луча определяется законом Декарта-Снеллиуса и в нашем случае он может быть записано в форме:
 ;
; 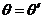 , (6.2)
, (6.2)
где nj , j, 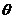 относятся к значению z, а
относятся к значению z, а  ,
, 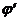 ,
, 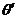 - к значению z’ ( z и z ’ определяют две произвольно выбранные плоскости, параллельные плоскости ху
- к значению z’ ( z и z ’ определяют две произвольно выбранные плоскости, параллельные плоскости ху
С учетом соотношений (6.2) , малости приращений d j и d J и учитывая, что:
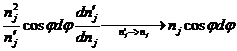 ,
,
получим:
 ,
,  . (6.3)
. (6.3)
Перемножая почленно первое равенство из (6.2) и оба равенства (6.3) и принимая во внимание, что sinj d j d 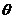 и sinj ’ d j ’ d
и sinj ’ d j ’ d 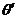 представляют собой элементы телесных углов dW и dW’, в которых лежат лучи из интервалов d j d
представляют собой элементы телесных углов dW и dW’, в которых лежат лучи из интервалов d j d 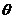 и d j ’ d
и d j ’ d 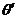 , получим следующее соотношение:
, получим следующее соотношение:
 . (6.4)
. (6.4)
Далее учтем, что в плоскослоистой среде с a w= 0 и m j =0и при стационарном распределении интенсивности вдоль лучей закон сохранения энергии требует, чтобы потоки энергии через одинаковые площадки dS и dS', сквозь которые проходит рассматриваемый луч в плоскостях z и z', были равны между собой. Поток энергии через dS равен I wcosj dWdS и, следовательно, равенство потоков через dS = dS' приводит к соотношению:
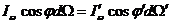 (6.5)
(6.5)
(I w — интенсивность вдоль луча в точке z , I w ’ - то же самое, но в точке г'). Деля почленно равенство (6.5) на (6.4), получаем:
 .
.
Поскольку плоскости z и z' были выбраны произвольно, отсюда следует, что в прозрачной (m j = 0) и неизлучающей ( a w = 0) плоскослоистой среде со стационарным распределением интенсивности I w (l) имеет место следующий инвариант вдоль луча:
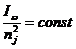 . (6.6)
. (6.6)
Тот же инвариант соблюдается в изотропной среде с произвольным (но плавным) характером неоднородности.
Посмотрим теперь, каким образом учет этого инварианта в неоднородной среде меняет вид уравнения переноса. Согласно (6.6) вносимое рефракцией изменение интенсивности на единице длины луча составляет:  или:
или:
 .
.
В неоднородной среде с отличной от нуля излучательной способностью a w, и коэффициентом поглощения m j , величину (2 I w/nj) dnj / dl нужно добавить в правую часть уравнения переноса (6.1). В результате оно приобретет следующий вид:
 . (6.7)
. (6.7)
В магнитоактивной, прозрачной (m j =0), неизлучающей (a w =0) плазме имеет место следующий инвариант вдоль луча:

 .
.
Здесь 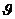 - угол между волновым вектором и групповой скоростью. В этом случае уравнение переноса принимает вид:
- угол между волновым вектором и групповой скоростью. В этом случае уравнение переноса принимает вид:

 . (6.8)
. (6.8)
Радиоизлучение в плоскослоистой, сферически-симметричной среде (солнечной короне)
Запишем закон Декарта-Снеллиуса:
 , (6.9)
, (6.9)
Конcтанта в (6.9) будет фиксирована, если задать угол j = j o между 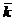 j и осью z на некотором уровне z = z 0 :
j и осью z на некотором уровне z = z 0 :
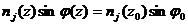 . (6.10)
. (6.10)
Часто в качестве уровня z 0 выбирают начало плазменного слоя e=1, где имеет место переход от плазмы к вакууму. Угол j 0 в этом слое называется углом падения волны на слой, значение nj { z 0 ) здесь равно единице для электромагнитных волн.
О поведении луча при наклонном падении волны под углом j 0 на плоскослоистую среду можно судить по рис. 6.2, а. Вершина луча, соответствующая точке отражения zref определяется из (6.10) при условии j=p/2:
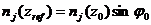 ,
,
или, что - то же самое (  ):
):
 . (6.11)
. (6.11)
Если в плазме находится источник, излучающий во всех направлениях, то благодаря рефракции излучение при выходе из плазмы приобретает направленный характер. Интервал углов j < j max под которыми излучение покидает среду, легко найти, если учесть, что луч, выходящий за пределы плазмы под наибольшим углом jmax имеет вершину в точке z=zsrc, где располагается источник (рис. 6.2, b).

a b
Рис. 6.2. Рефракция в плоскослоистой плазме с DN вдоль оси z : (а) форма луча, входящего в плазму под углом j o ; (b) лучи от точечного источника в плазме .
Тогда согласно (6.11):
 , (6.12)
, (6.12)
где  . Из этого выражения следует, что направленность увеличивается по мере приближения источника к уровню e ( z , w )=0 (либо за счет перемещения источника постоянной частоты в глубь плазмы, либо вследствие уменьшения частоты, генерируемой источником). Формула (6.12) позволяет оценить величину электронной концентрации в окрестности источника по наблюдаемой ширине углового спектра излучения на данной частоте.
. Из этого выражения следует, что направленность увеличивается по мере приближения источника к уровню e ( z , w )=0 (либо за счет перемещения источника постоянной частоты в глубь плазмы, либо вследствие уменьшения частоты, генерируемой источником). Формула (6.12) позволяет оценить величину электронной концентрации в окрестности источника по наблюдаемой ширине углового спектра излучения на данной частоте.
Закон преломления в сферически-симметричной среде:
 . (6.13)
. (6.13)
Если обозначить через R ¥ точку на траектории луча вне среды, то этому закону преломления можно придать следующий вид:
 , (6.14)
, (6.14)
где r - "прицельный параметр", характеризующий расстояние от входящего в среду луча до идущего параллельно ему радиуса. На Солнце параметр r имеет смысл расстояния от центра солнечного диска. Для поперечных электромагнитных волн показатель преломления за пределами короны nj ( R ¥ ) = 1 учет формального отличия nj ( R ¥ ) от единицы нужен лишь при рассмотрении рефракции плазменных волн. Типичный ход луча в солнечной короне с монотонно убывающей при увеличении R электронной концентрацией приведен на рис. 6.3.

a)
b)
Рис. 6.3a,b. К расчету формы луча в сферически-симметричной солнечной короне
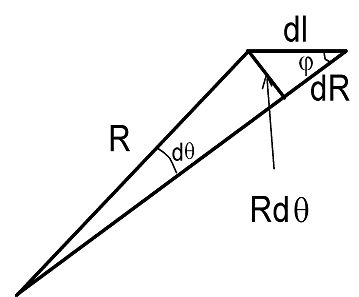
Из (6.14) и этого рисунка ясно, что элемент длины луча:
 (6.15)
(6.15)
Так как  , то
, то  и тогда траектория луча в полярных координатах R , q:
и тогда траектория луча в полярных координатах R , q:
 . (6.16)
. (6.16)
Величина q ¥, очевидно, совпадает с j ( R ¥ ). Точка отражения (точка "поворота"), где j = p/2, R = R* и q = q*, определяется равенством:
 . (6.17)
. (6.17)
Траектория луча симметрична относительно радиуса R*, проходящего через точку поворота, и лежит в плоскости, проходящей через центр симметрии.



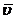 в правую часть уравнения движения электрона (4.3). То есть теперь мы имеем:
в правую часть уравнения движения электрона (4.3). То есть теперь мы имеем: .
.
 .
.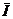 -i[
-i[  ]+X
]+X  =0.
=0.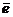 - единичный орт вдоль волнового вектора):
- единичный орт вдоль волнового вектора):
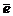
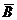 или
или  n[
n[  или n[
или n[ 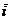 + Ye
+ Ye 

 =
=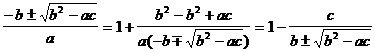 , получаем формулу Аппельтона-Хартри:
, получаем формулу Аппельтона-Хартри: .
. ,
, ,
,  . (5.2)
. (5.2) .
. ) и в широком интервале углов a , где реализуется случай квазипродольного распространения, оптическая толщина:
) и в широком интервале углов a , где реализуется случай квазипродольного распространения, оптическая толщина: . (5.3)
. (5.3) = BT –3/2 N 2 L , где L - толщина слоя. При написании формулы (5.3) учтено, что:
= BT –3/2 N 2 L , где L - толщина слоя. При написании формулы (5.3) учтено, что: ,
,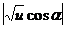 выражения (5.2). Яркостная температура теплового тормозного излучения из слоя Т b1,2= Т(1 -
выражения (5.2). Яркостная температура теплового тормозного излучения из слоя Т b1,2= Т(1 - 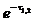 ) и на частотах w 2 << w cr 2 будет равна Т для обоих типов волн. Степень поляризации излучения на этих частотах равна нулю. В области w 2 >> w cr 2 слой становится оптически тонким, Т b1,2= T t1,2- Поскольку t1> t2(см. (5.3)), отсюда заключаем, что наложение магнитного поля на плазму увеличивает интенсивность тормозного излучения на необыкновенной волне, снижая одновременно излучение обыкновенной компоненты. Суммарная интенсивность I w µ Tb 1 + Tb 2 при этом не меняется (точнее, она возрастает в более высоком приближении по степеням
) и на частотах w 2 << w cr 2 будет равна Т для обоих типов волн. Степень поляризации излучения на этих частотах равна нулю. В области w 2 >> w cr 2 слой становится оптически тонким, Т b1,2= T t1,2- Поскольку t1> t2(см. (5.3)), отсюда заключаем, что наложение магнитного поля на плазму увеличивает интенсивность тормозного излучения на необыкновенной волне, снижая одновременно излучение обыкновенной компоненты. Суммарная интенсивность I w µ Tb 1 + Tb 2 при этом не меняется (точнее, она возрастает в более высоком приближении по степеням  .
. и излученной энергии
и излученной энергии  :
: 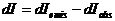 .
.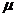 и длине пройденного пути
и длине пройденного пути  :
: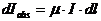 .
. к
к  . Величина
. Величина  .
.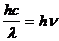 <<
<< 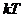 и формула Планка переходит в формулу Релея-Джинса:
и формула Планка переходит в формулу Релея-Джинса: .
.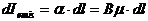 .
.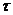 как
как
 . Следовательно:
. Следовательно: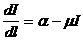 ,
, . (6.1)
. (6.1) )
) 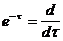 (
(  )
) 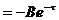 .
. , находим:
, находим: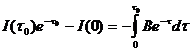 ,
,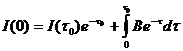 .
. и
и 
 или в температурах
или в температурах  .
.
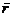 ). Будем предполагать, что изотропная плазма - плоскослоистая, т. е. ее показатель преломления nj зависит только от одной декартовой координаты z . Учет рефракции в этом случае значительно упрощается.
). Будем предполагать, что изотропная плазма - плоскослоистая, т. е. ее показатель преломления nj зависит только от одной декартовой координаты z . Учет рефракции в этом случае значительно упрощается. ;
; 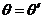 , (6.2)
, (6.2)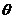 относятся к значению z, а
относятся к значению z, а  ,
, 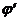 ,
, 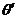 - к значению z’ ( z и z ’ определяют две произвольно выбранные плоскости, параллельные плоскости ху
- к значению z’ ( z и z ’ определяют две произвольно выбранные плоскости, параллельные плоскости ху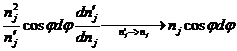 ,
, ,
,  . (6.3)
. (6.3) . (6.4)
. (6.4)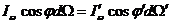 (6.5)
(6.5) .
.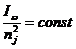 . (6.6)
. (6.6) или:
или: .
. . (6.7)
. (6.7) .
.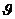 - угол между волновым вектором и групповой скоростью. В этом случае уравнение переноса принимает вид:
- угол между волновым вектором и групповой скоростью. В этом случае уравнение переноса принимает вид: . (6.8)
. (6.8) , (6.9)
, (6.9)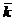 j и осью z на некотором уровне z = z 0 :
j и осью z на некотором уровне z = z 0 : 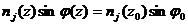 . (6.10)
. (6.10)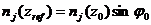 ,
, ):
): . (6.11)
. (6.11)
 , (6.12)
, (6.12) . Из этого выражения следует, что направленность увеличивается по мере приближения источника к уровню e ( z , w )=0 (либо за счет перемещения источника постоянной частоты в глубь плазмы, либо вследствие уменьшения частоты, генерируемой источником). Формула (6.12) позволяет оценить величину электронной концентрации в окрестности источника по наблюдаемой ширине углового спектра излучения на данной частоте.
. Из этого выражения следует, что направленность увеличивается по мере приближения источника к уровню e ( z , w )=0 (либо за счет перемещения источника постоянной частоты в глубь плазмы, либо вследствие уменьшения частоты, генерируемой источником). Формула (6.12) позволяет оценить величину электронной концентрации в окрестности источника по наблюдаемой ширине углового спектра излучения на данной частоте. . (6.13)
. (6.13) , (6.14)
, (6.14)

 (6.15)
(6.15) , то
, то  и тогда траектория луча в полярных координатах R , q:
и тогда траектория луча в полярных координатах R , q: . (6.16)
. (6.16) . (6.17)
. (6.17)

