Многие экономико-управленческие задачи являються многоцелевыми, в силу этого решение по одному критерию может оказаться не наилучшим по другим. Для решен подобн задач исп метод векторн оптимизац.
Множество критериев можно представить в виде векторной целевой ф-ии:
F(x) = (f1(x) f 2 ( x ),…, fk ( x ))
Для минимизации частного критерия fk ( x ) достаточно максимизировать - fk ( x ), т. к.
min fk ( x ) = max (- fk ( x )), поэтому каждый компонент векторного критерия максимизируется.
Задача: 1. max F (x) = (f1(x) f 2 ( x ),…, fk ( x ))
2. φi(x) {<=,=,>=}b, i= 1,n
3. xij >=0, j=1,n
Будем рассматривать эту задачу для случая, когда оптимальные решения xk, k= 1, k , полученные при решении по каждому критерию не совпадают. Найти решения, при которых значения всех критериев одновременно будет наилучшим можно в области компромисса, кот в ОДР.
Решения, которые доставляют критериям наилучшие значения называются – эффективными, компромиссными, оптимальными по Паретто.
План Х1 не хуже плана Х2, если fk(x1)>=fk(x2), k=1,n. Если среди последних неравенств хотя бы одно строгое, то план Х1 называется предпочтительнее плана Х2./ План Х1 оптимален по Паретто, если он допустим и не существует другого плана Х2, для которого fk(x1)>=fk(x2), k=1,n и хотя бы для 1-го критерия выполняется строгое неравенство.
Основные проблемы, возникающие при решении задач векторной оптимизации.
Проблема нормализации. Возникает в связи с тем, что локальные критерии имеют различные ед-цы и масштабы измерения, что делает невозможным их непосредственное сравнение. Для этого приходится приводить их к единому масштабу и безразмерному виду – нормировать. Самые распространённые способы нормирования: - замена абсолютных значений критериев их безразмерными относительными величинами: fk = fk/f*k, k=1,n; - замена абсолютных значений критериев их относительными значениями отклонений от оптимальных значений 
1. Проблема учёта приоритетов критерия. Здесь приходится находить как математическое, так и специальное влияние критерия на решение задачи.
2. Проблема определения области компромисса.
Методы решения многоцелевых задач
Методы решения многоцелевых задач делятся на:
-методы, кот основаны на свёртывании критериев -методы, в кот используются ограничения на критерии, -методы, которые основаны на отыскании компромиссного решения.
Наиболее распространёнными среди них являются:
1.Метод линейной комбинации частных критериев 2.Метод оследовательных уступок 3.Метод ведущего критерия 4.Метод равных и наименьших относительных отклонений
Метод лин.комбинаций част.критериев.
При решении задач данным методом вводится вектор весовых коэф.,кот.характ.важность соотвюкритерия.
α=(α1,α2,…αк), αк>0
Тогда целевая ф-ция будет представлять собой един.частных критериев,умноженных на весовые коэф.При этом критерии обязат.должны быть нормированы.
maxF(x)=Сумм αк*fк(x)
λi(x){<= >=}bi,i=1,m
xj>=0,j=1,n
Метод ведущего критерия.
Этот метод явл.частным случаем метода последовательных уступок.В этом методе все критерии,кроме маиого важного,переводятся в разряд ограничений.
Умножив все критерии минимизации ф-ции на -1 и обозначив через ß=(ß2,ß3..ßк)нижние границы соотв.критериев,тогда модель задачи будет меть вид:
maxF(x)=f1(x)
fk(x)>=ßk, k=2,k
λi(x){<=,=,>=}bi,i=1,m
xj>=0,j=1,n
Будем решать задачу по к критериям:
max f1 = 
max f2 = 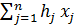
min fk = 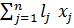 , k=3,k
, k=3,k
 ( ≤ , = , ≥ ) bi , i=1,m
( ≤ , = , ≥ ) bi , i=1,m
xj ≥ 0, j=1,n
Запишем условия равенства относит.отклонений критериев от их экстримальн.значений.
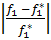 =
=  =…=
=…= 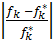
Рассмотрим 4 первых критерия. По условию задачи f1 и f2 максимизир-ся, а f3, f4-минимизир-ся. Проанализируем знач-я 2-х первых критериев.
Если 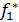 <0 и f*2<0 , то
<0 и f*2<0 , то
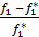 >0 и
>0 и 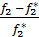 >0 Если f1*>0 и f2*>0 , то
>0 Если f1*>0 и f2*>0 , то 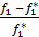 <0 и
<0 и 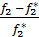 <0.
<0.
Поэтому в равенстве относит.отклонений этих критериев модуль абсолютных величин можно опустить. Тогда получим:
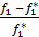 =
= 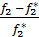 =>
=> 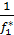 f1-1=
f1-1= 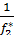 f2-1Введем обознач: d1=
f2-1Введем обознач: d1= 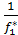 , d2 =
, d2 = 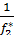 => d1f1-d2f2=0
=> d1f1-d2f2=0
Для критериев f3, f4 получим точно такое же уравнение, т.к. направления их оптимизации совпадают.Рассмотрим критерии с противоположными направлениями оптимизации f1и f3.Если f1*<0,
f3*<0, то 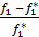 >0,
>0,  <0. Если f1*>0, f3*>0, то
<0. Если f1*>0, f3*>0, то 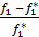 <0,
<0,  >0.
>0.
Поэтому при опускании знака модуль перед одним из выражений надопоставить «-». Получим: 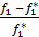 = -
= -  => d1f1+d3f3=2
=> d1f1+d3f3=2
Т.о., для нахождения компромиссного решения методом равных и наим. относ. отклонений необх. оптимизир-е критерии включить в число неизвестных задачи и к основным ограничениям добавить след. ограничения: d1f1-d2f2=0 – для всех fk, кот. как и f1 максимизир-ся; d1f1+d3f3=2 - для всех fk, кот.





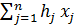
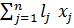 , k=3,k
, k=3,k ( ≤ , = , ≥ ) bi , i=1,m
( ≤ , = , ≥ ) bi , i=1,m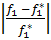 =
=  =…=
=…= 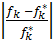
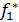 <0 и f*2<0 , то
<0 и f*2<0 , то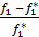 >0 и
>0 и 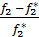 >0 Если f1*>0 и f2*>0 , то
>0 Если f1*>0 и f2*>0 , то 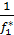 f1-1=
f1-1= 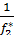 f2-1Введем обознач: d1=
f2-1Введем обознач: d1= 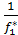 , d2 =
, d2 =  <0. Если f1*>0, f3*>0, то
<0. Если f1*>0, f3*>0, то 


