Понятие и виды коррел. и регресс. Задачи коррел. и регресс. ан-за
В эк-ке между явл. и проц. сущ. 2 вида завис-тей: функц-ная и статистич. 1-ая им. место тогда, когда на исслед. показатель действ. только рассматр. факторы.
В эк-ке между перемен. велич-ми сущ. завис., когда кажд. знач. одной переменной соответ. мн-во знач. др.перем-ой-статистич. завис-ть(стохастич., вероятностная).
В силу неодназнач. стат. завис-ти между Х и У интерес представ. завис-ть как независ. Х влияет на завис. переем. У «в среднем», т.е. завис-ть в измер. мат. ожид. случ. перемен. У, вычесл-го в предполож., что Х приним. знач. х-коррел. завис-ть, кот. можно опис. с пом. ф-ции регрессии У по Х: М(У/Х=х)=М(У/х)=Мх(У)=f(x) (1)
Зависим. перемен. У наз. объясняемой, выходной, эндоген.
Независ. перемен. Х наз. объясняющ., входной, экзаген.
При рассмотр. завис-ти двух случ. величин говор. о парн. завис-ти, а завис-ть мн. перемен. наз. множеств. регрессией М(У/х1,х2,…,хm)=f(х1,х2,…,хm)
Различ. след. виды регрессий:
1)простая (парная)-завис-ть между двумя перемен.
2)множеств.-завис-ть между завис. перемен. и неск. независ.перем.
3)линейн.-опис. лин. ф-цией
4)нелин.-опис. нелин.ф-цией
5)положит.-с увелич. или.сниж. независ. переем. соотв-но увелич. или сниж. зависимая
6)отриц.- с увелич. или.сниж. независ. переем. соотв-носниж.или увелич. зависимая
7)непосредств.-завис. и независ. перемен. связ. между собой
8)косвен.-независ. перем. действ. на завис.через др. переем.
9)ложная-строится, если между перем.отсутств. завис-ть
Задачи регресс. ан-за:
· уст. вида завис-ти между эк. перемен.
· опред. ф-ции регрессии
· опред. неизвест. знач.зависим.перемен.
Корр-ция тесно связ. с регрессией. Если в регресс. ан-зе исслед-ся форма завис-ти , то в коррел.-сила, степень этой завис-ти.
Задачи коррел. ан-за:
· измер. степени завис-ти 2или более эк-ких показат.
· отбор факторов, оказ-х наиболее сильн.влиян. на завис. перем.
· обнаруж. неизвест. завис-тей
Парн. лин. регресс.(ПЛР)
ПЛР- лин. ф-ция между усл. мат. ожид-ем М(У/хi) завис.перем. У и одной независ. переем.Х.
М(У/хi)=β0+β1хi, i=1͞,n, где хi-знач. независ. перем.в i-том наблюд. (1).
Для отраж. факта, что кажд. индивид. знач. уi отклон. от соответ. усл-го мат.ожид.,в формулу (1) необход. ввести случ. слог.εi: уi=М(У/хi)+εi=β0+β1xi+εi, i=1͞,n – теоретич. регресс-ная лин. модель.
β0 и β1- теоретич. коэф.регрес.
εi- теор. случ. отклон.
В общ. виде теор. лин. регресс. модель можно запис.: У=β0+β1Х+ε
По выборке огранич. объема (хi;уi), i=1͞,n можно постр. эмпирич. ур. регресс.:у͞i=в0+в1хi, i=1͞,n,(2) где уi͞͞-оценка усл-го мат. ожид.-М(У/хi), в0 и в1-оц-ки теор. коэф.регрес., кот. наз.эмпирич. коэф-ми => уi=у͞i +ei, i=1͞,n,(3) где еi – оц-ка случ. отклон. εi.
Поскольку генер. сов-ть практич. всегда неизвестна, то оценен. парам. в0 и в1 практич. всегда отлич. от истин. знач. β0 и β1. (рис). Задача сост. в том, чтобы по конкрет. выборке найти такие в0 и в1, чтобы построен. линия регрессии явл. бы наилучш. среди всех др.прямых, т.е. была наиближ. ко всем наблюд. по их сов-сти.
М-д наим. квадратов.
Для нахождения b0 и b1 м. использовать несколько м-дов: МНК, м-д моментов, max-го правдоподобия.
Согласно МНК эмпирические коэф-ты регр. b0 и b1 опр-ются из того факта, что Σ квадратов расстояний эмпирич. Знач-ий зав-мой перем-ой yi от расч. знач-ий yi^ д.б. миним-ой.
Q(b0,b1)=Σ(i=1,n)(yi-yi^)2=Σ(i=1,n)(y1-b0-b1xi)2 → min
Необходимым условием существования min в ф-ии переем-ых явл. равенство 0 ее частных производных по неизвестным параметрам b0 и b1:
Знак с-мы.:δQ/δb0=-2Σ(i=1,n)(y1-b0-b1xi)=0
δQ/δb1=-2Σ(i=1,n)(y1-b0-b1xi)xi=0
δ(частная производная)
З.с.: Σb0+Σb1xi=Σyi
Σb0xi+Σb1x2i=Σxiyi
З.с.: nb0+b1Σxi=Σyi
B0Σxi+b1Σx2i=Σxiyi
Разделим все на n:
Для практич-х расчетов последние ф-лыприменять не рекомендуется, т.к. в них происх. округление данных.
Лучше ипольз-ть след. ф-лы:
b1=(nΣxiyi-ΣxiΣyi)/(nΣx2i-(Σxi)2)
b0=(Σx2iΣyi-ΣxiΣxiyi)/(nΣxi-(Σxi)2).
Коэф-т корреляции
Перейдем к оценке тесноты коррел. зав-ти.
Подставим в знач. b0 из b0=yˉ-b1xˉ в yi^=b0+b1xi, i=1,n.
Получим: yi^=yˉ-b1xˉ+b1xi, yi^-yˉ=b1(xi-xˉ), i=1,n
Коэф-т b1 наз. коэф-том регрессии Y по X, кот. пок-ет насколько единиц в среднем изменяется переменная Y при изменении перем-ой X на 1ед.
В кач-ве пок-ля тесноты связи коэф-та регрессии b1 использовать не рекоменд-ся, т.к. он зав-т от ед-ц измерения, поэтому д/оц-ки тесноты связи исп-ются ср. квадратич. отклон-ие.Коэф-т b1 м. вычислить по ф-ле:
b1=(xy―-x–y–)/(x2–-x–2)=Sxy /S2x, где Sxy=xy―-x–y– – выборочная ковариация (совместное изменение).
Sx=√D=√(x2–-x–2) – выборочное ср. квадратич. отклонение.Тогда м. записать:
b1=Sxy/(Sx·Sy)·Sy/Sx=rxy(Sy/Sx), где rxy=Sxy/(Sx·Sy) – выборочный коэф-т коррел., хар-ет тесноту лин. зав-ти м/д случ. величинами.Для практич. расчетов коэф-т коррел. лучше использ-ть ф-лу:
rxy=(nΣxiyi-ΣxiΣyi)/√(nΣx2i-(Σxi)2)·√(nΣy2i-(Σyi)2).
Коэф-т коррел. изменяется в пределах -1≤rxy≥1
Если коэф-т кор. =0, то это зн., что случ. величины Х и У некоррелированные, если rxy≠0, то тогда случ. величины Х и У наз. коррелировнные. Если rxy=1 (строго), то в этом сл. говорят, что имеет место полная прямая коррел-я.
Если rxy≠1 – полная обратная коррел.
Если 0<rxy<1, то коррел. наз. положительной, это зн., что с возрастанием одной перем-ой вторая т-же возрастает.
Если -1<rxy<0 – отрицательная.
Чем ближе коэф-т коррел. к ±1, тем сильнее лин. зав-ть.
Обратная модель.
Обратной моделью(гипербола) называется модель вида: У= β0+ β1 1/Х + ε. Она сводится к линейной модели заменой 1/Х=Х*.
Данная модель применяется в тех случаях, когда неограниченное увеличение объясняющей переменной Х асимптотически приближает зависимую переменную У к к некоторому пределу β0.
12. Множ.лин.регр-сия.Опред-е парам-в ур-ния регр-сии. На люб.экон.показатель чаще всего оказыв.влияние не 1, а неск.факторов.В этом случ.вместо парной рассм-ся множеств.регр-ссия:М(Y/x1,x2…,xm)=f(x1,x2,…,xm). Ур-ние множ.регр-сии в общ.виде: Y=f(β,X)+ε, где β=( β0, β1,…, βm)-вектор теоретич.коэф-тов,кот.нужно определить. X=(X1,X2,…,Xm)-вектор независ.переменных. Теоретич.лин.ур-ние множ.регр-сии имеет вид:Y= β0+β1X1+β2X2+…+βmXm+ε или в кажд.конкр. случае: yi= β0+ β1xi1+β2xi2+…+ βmxim+εi, i= 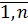 . Число степеней свободы для множ.лин.регр-сии: ѵ=n-m-1. Если n>m+1, то возник-ет необх-сть оценив-ния теорет.коэф-тов регр-сии. Будем исполь-ть метод наим.квадр-в.Должны выполняться предпосылки Гаусса-Маркова и еще 2 предпос-ки:а) отсутствие мультиколлинеарности,т.е. между независ.перемен-ми должна отсутсв-ть сильная лин.завис-сть b)случ.отклонения εi, i=
. Число степеней свободы для множ.лин.регр-сии: ѵ=n-m-1. Если n>m+1, то возник-ет необх-сть оценив-ния теорет.коэф-тов регр-сии. Будем исполь-ть метод наим.квадр-в.Должны выполняться предпосылки Гаусса-Маркова и еще 2 предпос-ки:а) отсутствие мультиколлинеарности,т.е. между независ.перемен-ми должна отсутсв-ть сильная лин.завис-сть b)случ.отклонения εi, i= 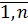 должны иметь норм.распред-ние εi ~ N(0,6). Истинные значения коэф-тов по выборке опред-ть невозможно, поэтому строится импирич.ур-ние регр-сии: Ŷ= b0+b1X1+b2X2+…+bmXm. Для каждого наблюдения мы получим: yi=ŷi+ei, i=
должны иметь норм.распред-ние εi ~ N(0,6). Истинные значения коэф-тов по выборке опред-ть невозможно, поэтому строится импирич.ур-ние регр-сии: Ŷ= b0+b1X1+b2X2+…+bmXm. Для каждого наблюдения мы получим: yi=ŷi+ei, i= 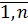 . Для нахождения оценок b0,b1,…,bm исполь-ся ф-ция Q(b0,b1,…,bm)=
. Для нахождения оценок b0,b1,…,bm исполь-ся ф-ция Q(b0,b1,…,bm)=  =
= 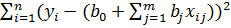 →min. Дан.ф-ция-квадратичная. Необх.условие сущ-ния минимума-рав-во нулю всех ее частн.производных
→min. Дан.ф-ция-квадратичная. Необх.условие сущ-ния минимума-рав-во нулю всех ее частн.производных
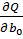 =-2
=-2 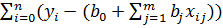 =0, i=
=0, i= 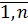
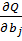 =-2
=-2 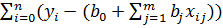 xij=0, j=
xij=0, j= 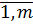 .
.
Статистика Дарбина-Уртсона
Прим-ся для анализа коррелируемости случ. отк-ний. Опр-ся по формуле:
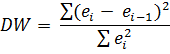
Для больших значений n счит-ся, что 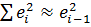 , тогда:
, тогда:
 =
= 
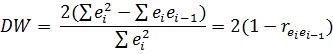
1 случай. Если 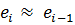 , то
, то  , DW = 0
, DW = 0
2 случай. 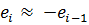 , то
, то 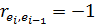 , DW = 4
, DW = 4
3 случай. 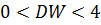
Т.к. абсолютн. значение случ. откл-ний в среднем одинаково, то:

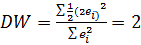
Поэтому необходим. условием незав-ти случ. откл-ний явл-ся близость к 2 значения DW .
“Грубым” правилом можно считать отсутствия автокорр-ции, если 1,5<DW<2,5.
Степенная модель
Степенной моделью называетсямодель вида Y=β0+β1X+β2X2+…+βmXm+ε.
Например, кубическая функция Y=β0+β1X+β2X2+β3X3+ε в микроэкономике моделирует зависимость издержек TC от объёма выпуска Q (рис. а).
Квадратичная функция (парабола) Y=β0+β1X+β2X2 +ε может отражать зависимость между объёмом выпуска Q и средними AC либо предельными MC издержками (рис. б), или между расходами на рекламу C и прибылью P (рис. в) и т.д.
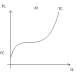
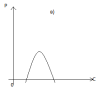

Модель является линейной относительно коэффициентов регрессии β0, β1,…βm.
Следовательно, её можно свести к линейной регрессионной модели. Заменяя X на X1, X2 на X2, Xm на Xm, получаем модель множественной линейной регрессии с m переменными X1, X2,….Xm:
Y=β0+β1X1+β2X2+…+βmXm+ε.
23/Полулогарифмические модели.
Полулогарифмическими моделями называют модели вида:
lnУ=β0+ β1Х+ ε
У= β0+ β1 lnХ+ε.
Такие модели обычно используются в тех случаях, когда необходимо определятьтемп роста или прироста каких-либо экономических показателей.
Лог-линейная модель.Рассмотрим зависимость У=У0 (1+r)t,
Где У0 – начальная величина переменной У (начальный капитал), r – процентная ставка, У1 – значение переменной У в момент времени t. Модель легко сводится к полулогарифмической модели:
lnУ= lnУ0+ t ln(1+r). обозначим lnУ0=β0, ln(1+r)=β1,тогда:lnУt=β0+ β1t+ εt.
случайное слагаемое εt – возможность изменения процентной ставки.
Заменой lnУt=Уt* полулогарифмическая модель легко сводится к линейной модели.
Коэф.β1 имеет смысл темпа прироста переменной У по переменной Х,т.е.характеризует отношение относительного изменения У к абсолютному изменению Х. умножив β1 на 100, получим процентное изменение переменной У. поэтому полулогарифмическая модель обычно используется для измерения темпа прироста экономических показателей.
Показательная модель
Показательная модель: Y=β0eβ1X
Важным её приложением является ситуация, когда анализируется изменение переменной Y с постоянным темпом прироста во времени. В этом случае переменная X символически заменяется переменной t: Y= β0eβ1t . Данная функция путём логарифмирования сводится к лог-линейной модели: lnY=lnβ0+β1t.
В общем случае Y=β0aβ1X , где а – произвольная положительная константа, а≠1.
Данная функция сводится к исходной вследствие тождества: aβ1X=eβ1Xlna.
Ряд экономических показателей моделируется через функции, являющиеся композицией перечисленных функции, что позволяет свести их к линейным. Например, производственная функция Кобба-Дугласа с учётом научно-технического рогресса:
Y=AKaLβeγt
Пролагарифмируем данную функцию, получим соотношение:
lnY=lnA+aLnK+βlnL+γt, которое сводится к линейному заменами. lnY=y, lnA=a, lnK=k, lnL=l
27 - Преобразование случайного отклонения
Как отмечалось ранее, для получения качественных оценок существенную роль играет выполнимость предпосылок МНК для случайных отклонений. Наиболее важные из них требуют, чтобы отклонение εi, являлись нормально распределёнными случайными величинами с нулевым математическим ожиданием и постоянной дисперсией ϭ2, а также не коррелировали друг с другом: εi~N(0, ϭ2), cov(εi ,εj)=0 при i≠j, i,j=1,n. При невыполнимости указанных предпосылок оценки, полученные по МНК, не будут обладать свойствами BLUE-оценок.
В случаях, не требующих совокупного логарифмирования с аддитивным случайным членом, выполнимость предпосылок МНК имеет место, а следовательно, проблем с оцениваем не возникает.
Для описания возможных проблем со случайным отклонением воспользуемся степенной моделью Y=AXβ, выполнив её случайным членом. Рассмотрим три случая:
Y=AXβeε (1)
Y=AXβε (2)
Y=AXβ+ε (3)
Данные модели являются нелинейными относительно параметра β. Прологарифмировав каждое из этих соотношений, получим:
lnY=lnA+βlnX+ε (4)
lnY=lnA+βlnX+lnε (5)
lnY=ln(AXβ+ ε) (6)
Использование (4) для оценки параметров в (1) не вызывает осложнений, связанных со случайным отклонением.
Преобразование (2) в (5) приводит к преобразованию случайных отклонений εi в ln εi . Использование МНК в (5) для нахождения BLUE-оценок параметров требует, чтобы отклонение vi= ln εi, удовлетворяли предпосылкам МНК: vi~ N(0, ϭ2). Но это возможно только в случае логарифмически нормального распределения СВ εi с M(εi)=e^ ϭ2/2 и D(εi)= e^ ϭ2(e^ ϭ2-1) .
Логарифмирование соотношения (6) не приводит к линеаризации соотношения относительно параметров. В этом случае для нахождения оценок необходимо использовать определённые интерационные процедуры оценки нелинейных регрессий.
Таким образом, при использовании преобразований с целью нахождения оценок необходимо особое внимание уделять рассмотрению свойств случайных отклонений, чтобы полученные в результате оценки имели высокую статистическую значимость.
Метод ведущего критерия.
Этот метод явл.частным случаем метода последовательных уступок.В этом методе все критерии,кроме маиого важного,переводятся в разряд ограничений.
Умножив все критерии минимизации ф-ции на -1 и обозначив через ß=(ß2,ß3..ßк)нижние границы соотв.критериев,тогда модель задачи будет меть вид:
maxF(x)=f1(x)
fk(x)>=ßk, k=2,k
λi(x){<=,=,>=}bi,i=1,m
xj>=0,j=1,n
Будем решать задачу по к критериям:
max f1 = 
max f2 = 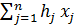
min fk = 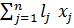 , k=3,k
, k=3,k
 ( ≤ , = , ≥ ) bi , i=1,m
( ≤ , = , ≥ ) bi , i=1,m
xj ≥ 0, j=1,n
Запишем условия равенства относит.отклонений критериев от их экстримальн.значений.
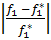 =
=  =…=
=…= 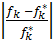
Рассмотрим 4 первых критерия. По условию задачи f1 и f2 максимизир-ся, а f3, f4-минимизир-ся. Проанализируем знач-я 2-х первых критериев.
Если 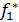 <0 и f*2<0 , то
<0 и f*2<0 , то
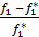 >0 и
>0 и 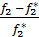 >0 Если f1*>0 и f2*>0 , то
>0 Если f1*>0 и f2*>0 , то 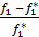 <0 и
<0 и 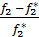 <0.
<0.
Поэтому в равенстве относит.отклонений этих критериев модуль абсолютных величин можно опустить. Тогда получим:
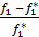 =
= 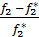 =>
=> 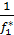 f1-1=
f1-1= 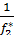 f2-1Введем обознач: d1=
f2-1Введем обознач: d1= 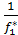 , d2 =
, d2 = 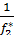 => d1f1-d2f2=0
=> d1f1-d2f2=0
Для критериев f3, f4 получим точно такое же уравнение, т.к. направления их оптимизации совпадают.Рассмотрим критерии с противоположными направлениями оптимизации f1и f3.Если f1*<0,
f3*<0, то 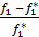 >0,
>0,  <0. Если f1*>0, f3*>0, то
<0. Если f1*>0, f3*>0, то 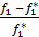 <0,
<0,  >0.
>0.
Поэтому при опускании знака модуль перед одним из выражений надопоставить «-». Получим: 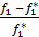 = -
= -  => d1f1+d3f3=2
=> d1f1+d3f3=2
Т.о., для нахождения компромиссного решения методом равных и наим. относ. отклонений необх. оптимизир-е критерии включить в число неизвестных задачи и к основным ограничениям добавить след. ограничения: d1f1-d2f2=0 – для всех fk, кот. как и f1 максимизир-ся; d1f1+d3f3=2 - для всех fk, кот.
Расч. врем. парам. событ.
Ранн. срок совершен. событ. j – t p(j) - самый ранн. момент врем., к к-му заверш. все предшеств. этому событ. раб.
Будем счит. t p(1) =0, а все послед. ранн. срок. событ. будем опред-ть по ф-ле:  ,
, 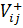 - множ. работ, вход. в j-ое событ.
- множ. работ, вход. в j-ое событ.
Поздн. срок свершен. событ. i, 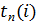 - сам. поздн. мом-т врем, после к-го остает. ровно стольк. врем., скольк. надо для завершен. всех раб. след. за этим событ.
- сам. поздн. мом-т врем, после к-го остает. ровно стольк. врем., скольк. надо для завершен. всех раб. след. за этим событ. 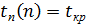 , а все остав-ся определ разност. м/ду
, а все остав-ся определ разност. м/ду 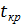 и длин максим из след путей
и длин максим из след путей 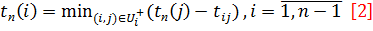 ,
, 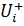 - множ. раб. выход. из i-го событ.
- множ. раб. выход. из i-го событ.
Резерв времен. соб i (R(i)) – разн-ть м/ду поздн и ранн срок. совершен. событ.: 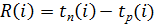
Все раб. событ., лежащ на крит. пути имеют нулев. резерв врем.
При расч времен парамет событ. удобно пользов. 4-х секторн схем .
1. В верхн сектор. проставл № событ.
2. Рассматр-ем событ. в порядке возрастан. № и считая, что t p(1) =0. По ф-ле 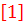 по входящ. в событ. раб. опр-ем
по входящ. в событ. раб. опр-ем 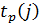 и запис-ем в лев. сектор.
и запис-ем в лев. сектор.
3. Перепис. в заверш. событ. число из лев. сект. в прав. и по обратн. №№ событ. по ф-ле 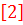 по выходн. раб. опр-ем
по выходн. раб. опр-ем 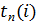 . Там, где R(i)=0 – крит. путь.
. Там, где R(i)=0 – крит. путь.
Расч времен парам раб.
Ранн. срок нач. раб. i,j = ранн. сроку соверш. событ. i :  .
.
Поздн. срок оконч. раб. i,j совпад. с поздн. срок соверш. событ. j:  .
.
Ранн срок. оконч. раб. i,j будем назыв. сумму ранн. срока начал. раб. и его продол-сти.: 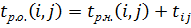 .
.
Поздн. срок. начал. раб. i,j бу-м назыв. разн. м/ду поздн. окончан. данн. раб. и ее продолж-сть: 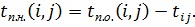
Полн. резер-м времен i,j наз-ся максим. возмож. запас врем., на к-рый можн. отложить нач. раб. или увелич. время ее выполнен. без увеличен. врем. (срока) выполнен. проект.: 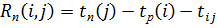 .
.
Понятие и виды коррел. и регресс. Задачи коррел. и регресс. ан-за
В эк-ке между явл. и проц. сущ. 2 вида завис-тей: функц-ная и статистич. 1-ая им. место тогда, когда на исслед. показатель действ. только рассматр. факторы.
В эк-ке между перемен. велич-ми сущ. завис., когда кажд. знач. одной переменной соответ. мн-во знач. др.перем-ой-статистич. завис-ть(стохастич., вероятностная).
В силу неодназнач. стат. завис-ти между Х и У интерес представ. завис-ть как независ. Х влияет на завис. переем. У «в среднем», т.е. завис-ть в измер. мат. ожид. случ. перемен. У, вычесл-го в предполож., что Х приним. знач. х-коррел. завис-ть, кот. можно опис. с пом. ф-ции регрессии У по Х: М(У/Х=х)=М(У/х)=Мх(У)=f(x) (1)
Зависим. перемен. У наз. объясняемой, выходной, эндоген.
Независ. перемен. Х наз. объясняющ., входной, экзаген.
При рассмотр. завис-ти двух случ. величин говор. о парн. завис-ти, а завис-ть мн. перемен. наз. множеств. регрессией М(У/х1,х2,…,хm)=f(х1,х2,…,хm)
Различ. след. виды регрессий:
1)простая (парная)-завис-ть между двумя перемен.
2)множеств.-завис-ть между завис. перемен. и неск. независ.перем.
3)линейн.-опис. лин. ф-цией
4)нелин.-опис. нелин.ф-цией
5)положит.-с увелич. или.сниж. независ. переем. соотв-но увелич. или сниж. зависимая
6)отриц.- с увелич. или.сниж. независ. переем. соотв-носниж.или увелич. зависимая
7)непосредств.-завис. и независ. перемен. связ. между собой
8)косвен.-независ. перем. действ. на завис.через др. переем.
9)ложная-строится, если между перем.отсутств. завис-ть
Задачи регресс. ан-за:
· уст. вида завис-ти между эк. перемен.
· опред. ф-ции регрессии
· опред. неизвест. знач.зависим.перемен.
Корр-ция тесно связ. с регрессией. Если в регресс. ан-зе исслед-ся форма завис-ти , то в коррел.-сила, степень этой завис-ти.
Задачи коррел. ан-за:
· измер. степени завис-ти 2или более эк-ких показат.
· отбор факторов, оказ-х наиболее сильн.влиян. на завис. перем.
· обнаруж. неизвест. завис-тей
Парн. лин. регресс.(ПЛР)
ПЛР- лин. ф-ция между усл. мат. ожид-ем М(У/хi) завис.перем. У и одной независ. переем.Х.
М(У/хi)=β0+β1хi, i=1͞,n, где хi-знач. независ. перем.в i-том наблюд. (1).
Для отраж. факта, что кажд. индивид. знач. уi отклон. от соответ. усл-го мат.ожид.,в формулу (1) необход. ввести случ. слог.εi: уi=М(У/хi)+εi=β0+β1xi+εi, i=1͞,n – теоретич. регресс-ная лин. модель.
β0 и β1- теоретич. коэф.регрес.
εi- теор. случ. отклон.
В общ. виде теор. лин. регресс. модель можно запис.: У=β0+β1Х+ε
По выборке огранич. объема (хi;уi), i=1͞,n можно постр. эмпирич. ур. регресс.:у͞i=в0+в1хi, i=1͞,n,(2) где уi͞͞-оценка усл-го мат. ожид.-М(У/хi), в0 и в1-оц-ки теор. коэф.регрес., кот. наз.эмпирич. коэф-ми => уi=у͞i +ei, i=1͞,n,(3) где еi – оц-ка случ. отклон. εi.
Поскольку генер. сов-ть практич. всегда неизвестна, то оценен. парам. в0 и в1 практич. всегда отлич. от истин. знач. β0 и β1. (рис). Задача сост. в том, чтобы по конкрет. выборке найти такие в0 и в1, чтобы построен. линия регрессии явл. бы наилучш. среди всех др.прямых, т.е. была наиближ. ко всем наблюд. по их сов-сти.
М-д наим. квадратов.
Для нахождения b0 и b1 м. использовать несколько м-дов: МНК, м-д моментов, max-го правдоподобия.
Согласно МНК эмпирические коэф-ты регр. b0 и b1 опр-ются из того факта, что Σ квадратов расстояний эмпирич. Знач-ий зав-мой перем-ой yi от расч. знач-ий yi^ д.б. миним-ой.
Q(b0,b1)=Σ(i=1,n)(yi-yi^)2=Σ(i=1,n)(y1-b0-b1xi)2 → min
Необходимым условием существования min в ф-ии переем-ых явл. равенство 0 ее частных производных по неизвестным параметрам b0 и b1:
Знак с-мы.:δQ/δb0=-2Σ(i=1,n)(y1-b0-b1xi)=0
δQ/δb1=-2Σ(i=1,n)(y1-b0-b1xi)xi=0
δ(частная производная)
З.с.: Σb0+Σb1xi=Σyi
Σb0xi+Σb1x2i=Σxiyi
З.с.: nb0+b1Σxi=Σyi
B0Σxi+b1Σx2i=Σxiyi
Разделим все на n:
Для практич-х расчетов последние ф-лыприменять не рекомендуется, т.к. в них происх. округление данных.
Лучше ипольз-ть след. ф-лы:
b1=(nΣxiyi-ΣxiΣyi)/(nΣx2i-(Σxi)2)
b0=(Σx2iΣyi-ΣxiΣxiyi)/(nΣxi-(Σxi)2).
Коэф-т корреляции
Перейдем к оценке тесноты коррел. зав-ти.
Подставим в знач. b0 из b0=yˉ-b1xˉ в yi^=b0+b1xi, i=1,n.
Получим: yi^=yˉ-b1xˉ+b1xi, yi^-yˉ=b1(xi-xˉ), i=1,n
Коэф-т b1 наз. коэф-том регрессии Y по X, кот. пок-ет насколько единиц в среднем изменяется переменная Y при изменении перем-ой X на 1ед.
В кач-ве пок-ля тесноты связи коэф-та регрессии b1 использовать не рекоменд-ся, т.к. он зав-т от ед-ц измерения, поэтому д/оц-ки тесноты связи исп-ются ср. квадратич. отклон-ие.Коэф-т b1 м. вычислить по ф-ле:
b1=(xy―-x–y–)/(x2–-x–2)=Sxy /S2x, где Sxy=xy―-x–y– – выборочная ковариация (совместное изменение).
Sx=√D=√(x2–-x–2) – выборочное ср. квадратич. отклонение.Тогда м. записать:
b1=Sxy/(Sx·Sy)·Sy/Sx=rxy(Sy/Sx), где rxy=Sxy/(Sx·Sy) – выборочный коэф-т коррел., хар-ет тесноту лин. зав-ти м/д случ. величинами.Для практич. расчетов коэф-т коррел. лучше использ-ть ф-лу:
rxy=(nΣxiyi-ΣxiΣyi)/√(nΣx2i-(Σxi)2)·√(nΣy2i-(Σyi)2).
Коэф-т коррел. изменяется в пределах -1≤rxy≥1
Если коэф-т кор. =0, то это зн., что случ. величины Х и У некоррелированные, если rxy≠0, то тогда случ. величины Х и У наз. коррелировнные. Если rxy=1 (строго), то в этом сл. говорят, что имеет место полная прямая коррел-я.
Если rxy≠1 – полная обратная коррел.
Если 0<rxy<1, то коррел. наз. положительной, это зн., что с возрастанием одной перем-ой вторая т-же возрастает.
Если -1<rxy<0 – отрицательная.
Чем ближе коэф-т коррел. к ±1, тем сильнее лин. зав-ть.



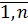 . Число степеней свободы для множ.лин.регр-сии: ѵ=n-m-1. Если n>m+1, то возник-ет необх-сть оценив-ния теорет.коэф-тов регр-сии. Будем исполь-ть метод наим.квадр-в.Должны выполняться предпосылки Гаусса-Маркова и еще 2 предпос-ки:а) отсутствие мультиколлинеарности,т.е. между независ.перемен-ми должна отсутсв-ть сильная лин.завис-сть b)случ.отклонения εi, i=
. Число степеней свободы для множ.лин.регр-сии: ѵ=n-m-1. Если n>m+1, то возник-ет необх-сть оценив-ния теорет.коэф-тов регр-сии. Будем исполь-ть метод наим.квадр-в.Должны выполняться предпосылки Гаусса-Маркова и еще 2 предпос-ки:а) отсутствие мультиколлинеарности,т.е. между независ.перемен-ми должна отсутсв-ть сильная лин.завис-сть b)случ.отклонения εi, i=  =
= 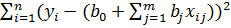 →min. Дан.ф-ция-квадратичная. Необх.условие сущ-ния минимума-рав-во нулю всех ее частн.производных
→min. Дан.ф-ция-квадратичная. Необх.условие сущ-ния минимума-рав-во нулю всех ее частн.производных 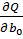 =-2
=-2 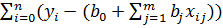 =0, i=
=0, i= 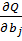 =-2
=-2 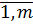 .
.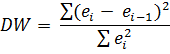
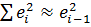 , тогда:
, тогда: =
= 
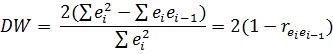
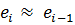 , то
, то  , DW = 0
, DW = 0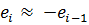 , то
, то 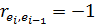 , DW = 4
, DW = 4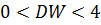

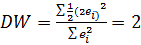




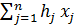
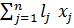 , k=3,k
, k=3,k ( ≤ , = , ≥ ) bi , i=1,m
( ≤ , = , ≥ ) bi , i=1,m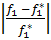 =
=  =…=
=…= 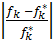
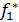 <0 и f*2<0 , то
<0 и f*2<0 , то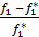 >0 и
>0 и 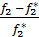 >0 Если f1*>0 и f2*>0 , то
>0 Если f1*>0 и f2*>0 , то 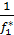 f1-1=
f1-1= 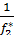 f2-1Введем обознач: d1=
f2-1Введем обознач: d1= 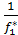 , d2 =
, d2 =  <0. Если f1*>0, f3*>0, то
<0. Если f1*>0, f3*>0, то  ,
, 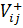 - множ. работ, вход. в j-ое событ.
- множ. работ, вход. в j-ое событ.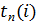 - сам. поздн. мом-т врем, после к-го остает. ровно стольк. врем., скольк. надо для завершен. всех раб. след. за этим событ.
- сам. поздн. мом-т врем, после к-го остает. ровно стольк. врем., скольк. надо для завершен. всех раб. след. за этим событ. 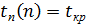 , а все остав-ся определ разност. м/ду
, а все остав-ся определ разност. м/ду 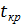 и длин максим из след путей
и длин максим из след путей 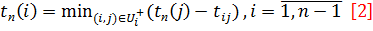 ,
, 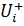 - множ. раб. выход. из i-го событ.
- множ. раб. выход. из i-го событ.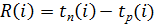
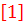 по входящ. в событ. раб. опр-ем
по входящ. в событ. раб. опр-ем 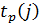 и запис-ем в лев. сектор.
и запис-ем в лев. сектор.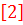 по выходн. раб. опр-ем
по выходн. раб. опр-ем  .
. .
.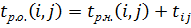 .
.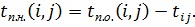
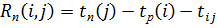 .
. 

