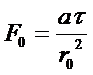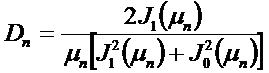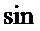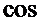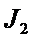Запишем решение нестационарных задач в декартовых координатах.



Начальные условия 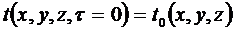 должны быть заданы.
должны быть заданы.
Граничное условие задаётся в виде граничных условий III рода:

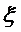 - любая координата (x, y, z).
- любая координата (x, y, z).
Кроме того, мы должны знать внешние параметры, то есть размеры 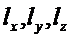
и теплофизические параметры: 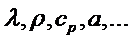
Незнание одного из условий переводит задачу в нерешаемую.
Поместим болванку в печь

- температура на оси или центральной пл-ти
Изменение температур в разных точках тела будет разным. На поверхности температура будет расти сразу, внутри – через некоторое время (время запаздывания). Имеет место разность температур в разных точках тела.
Охлаждение (нагревание) бесконечной пластины.
Задача решается одинаково и для нагрева и для охлаждения.
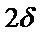

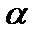
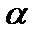



 Будем считать, что пластина бесконечна постоянной толщины
Будем считать, что пластина бесконечна постоянной толщины 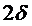 .
.
 Разместим начало координат в серединной плоскости.
Разместим начало координат в серединной плоскости.


Постоянное поле температур в начальный момент времени.
Известно: 

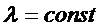
 Задача одномерная, пусть
Задача одномерная, пусть 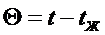
- уравнение теплопроводности
для нестационарной задачи.
Зададим ряд постоянных начальных условий:


Два граничных условия:
1) 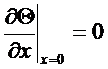 - условие симметрии. Температуры в симметричных точках относительно оси z равны. Будем решать задачу от 0 до
- условие симметрии. Температуры в симметричных точках относительно оси z равны. Будем решать задачу от 0 до  .
.
2) Граничные условия III рода:

Используем метод разделения переменных.
Предположим, что решение может быть представлено как произведение двух функций: одна функция зависит от времени, другая – от координат.

Ищем решение:
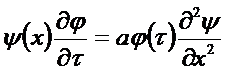
Пусть: 


 (*)
(*)
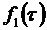
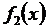
Эти функции могут быть равны, только если (*) = const.
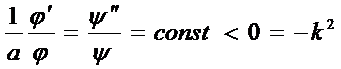
Решение первого уравнения: 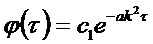
Решение второго уравнения: 
Воспользуемся условием симметрии:
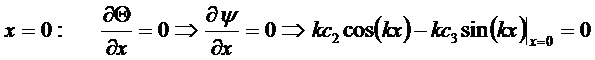
Отсюда 
Итак: 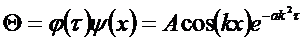 , где:
, где: 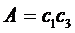 .
.

 Сгруппируем:
Сгруппируем: 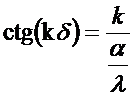 умножим на .
умножим на .
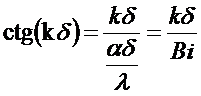
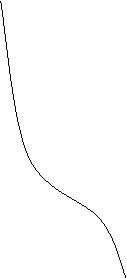
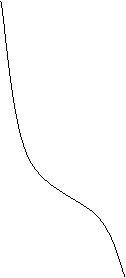
Обозначим: 

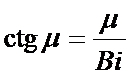
- характеристическое
уравнение для расчёта
корней 
 правая часть
правая часть
левая


 часть
часть
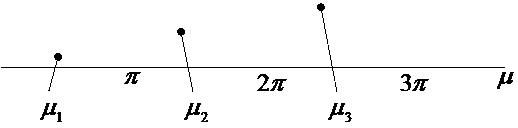
Решений этого характеристического уравнения бесконечное множество. Решению удовлетворяет множество принятых нами значений k.

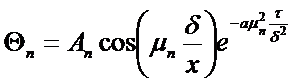
Введём безразмерную координату: 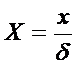
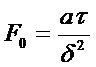 - критерий Фурье или безразмерное время.
- критерий Фурье или безразмерное время.
Общее решение задачи:

где: 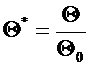 - безразмерное отношение разности температур.
- безразмерное отношение разности температур.
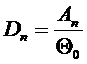
Согласно принятому начальному условию  :
:

через коэффициент А:

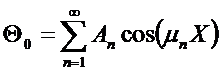 (*)
(*)
Разложение функции в ряд Фурье
(это четная функция)
Если мы возьмём область определения от 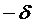 до
до  и проинтегрируем от
и проинтегрируем от  до
до  :
:

Домножим (*) на 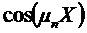 и проинтегрируем:
и проинтегрируем:

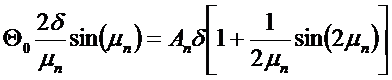
Константа Ап для любого частного решения определяется начальными условиями задачи:


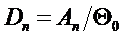
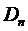
Анализ решения.
Поскольку в решение входит exp с отрицательным показателем, то при больших временах exp – бесконечно малое. Значит, ряд является быстро сходящимся. Если ряд быстро сходящийся, то можно ограничиться только первыми членами ряда. Большим временем можно считать  . Если
. Если  , то ограничиваются только первым членом ряда:
, то ограничиваются только первым членом ряда:




F(Bi) F(Bi,X)
В таблицах и монограммах рассчитано для двух точек (в середине пластины
Х =0 и на поверхности Х =1)

Одна монограмма для Х =0, другая – для Х =1
Случаи вырождения чисел БИО.
Вырождение – достижение некоторых предельных значений. Предельными значениями БИО являются бесконечно большие и бесконечно малые.
1) Бесконечно большое число Bi: 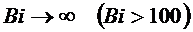 .
.
можно применять предельный подход:
при  :
: 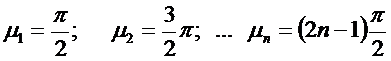
Если мы рассмотрим выражение для 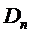 :
:
 причём:
причём: 
так как  , то
, то 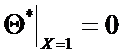
Изобразим это:
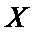
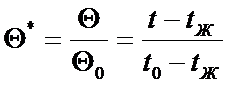
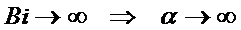
Если поместить пластину в печь, то температура на её поверхности сразу станет равной температуре печи.
Если 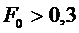 , мы получим:
, мы получим:
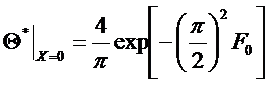 - температура на оси при больших временах.
- температура на оси при больших временах.
Выражая  через
через 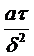 , мы получим:
, мы получим:

Это время достижения заданной температуры в центре пластины.
2) Бесконечно малое Био: 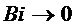
На практике Био вырождено, если 
Корни характеристического уравнения:
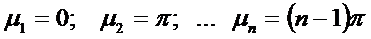
При этом: 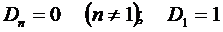
Для тонких тел температура описывается одним членом ряда независимо от числа 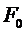 .
.

Определим порядок  при
при  :
:


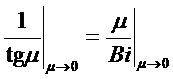

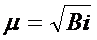
Поэтому для малых Био поле температур описывается одним единственным членом ряда:

Изобразим эту зависимость:





Это означает, что разница температур в центре и на поверхности стремится к нулю.
3) Рассмотрим  :
:

Охлаждение (нагревание) бесконечного цилиндра.
Рассмотрим бесконечный цилиндр радиусом  .
.
Известен материал, 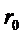 ,
,  . Цилиндр размещён в среде с постоянной
. Цилиндр размещён в среде с постоянной  , коэффициент теплоотдачи
, коэффициент теплоотдачи 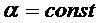 .
.
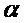
 Начальная температура в любой точке цилиндра
Начальная температура в любой точке цилиндра 
Задача является одномерной.


решением является: 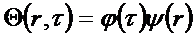

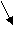





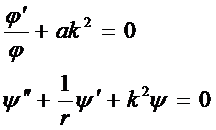
Почти уравнение Бесселя
его решениями являются функции Бесселя 
 - функция Бесселя первого рода нулевого порядка;
- функция Бесселя первого рода нулевого порядка;
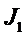 - функция Бесселя первого рода первого порядка.
- функция Бесселя первого рода первого порядка.
Начальные условия: 
Граничные условия:
1) 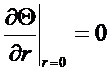 - условие симметрии.
- условие симметрии.
2) 
Общий вид решения:


 - безразмерный радиус.
- безразмерный радиус. 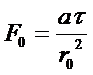
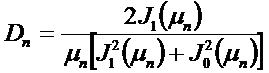
J0 – аналогично 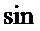
J1 – аналогично 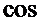






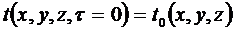 должны быть заданы.
должны быть заданы.
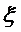 - любая координата (x, y, z).
- любая координата (x, y, z).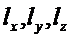
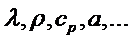





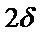

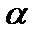



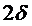 .
. Разместим начало координат в серединной плоскости.
Разместим начало координат в серединной плоскости.



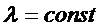
 Задача одномерная, пусть
Задача одномерная, пусть 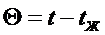


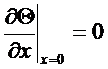 - условие симметрии. Температуры в симметричных точках относительно оси z равны. Будем решать задачу от 0 до
- условие симметрии. Температуры в симметричных точках относительно оси z равны. Будем решать задачу от 0 до  .
.

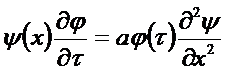



 (*)
(*)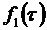
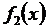
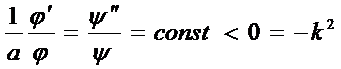
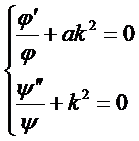
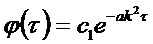

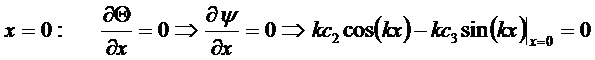

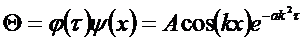 , где:
, где: 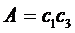 .
.
 Сгруппируем:
Сгруппируем: 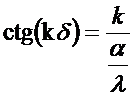 умножим на .
умножим на .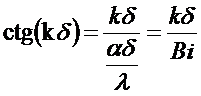


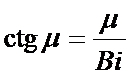





 правая часть
правая часть

 часть
часть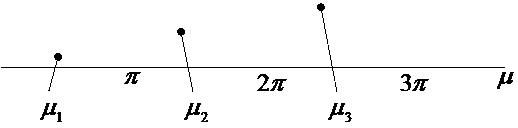

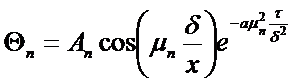
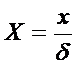
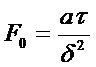 - критерий Фурье или безразмерное время.
- критерий Фурье или безразмерное время.
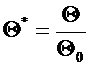 - безразмерное отношение разности температур.
- безразмерное отношение разности температур.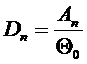
 :
:

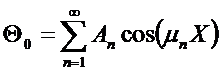 (*)
(*) 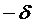 до
до  и проинтегрируем от
и проинтегрируем от  до
до  :
:
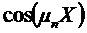 и проинтегрируем:
и проинтегрируем:
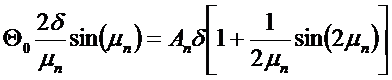


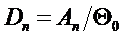
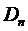
 . Если
. Если 





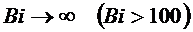 .
. :
: 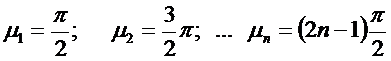
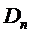 :
: причём:
причём: 
 , то
, то 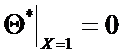



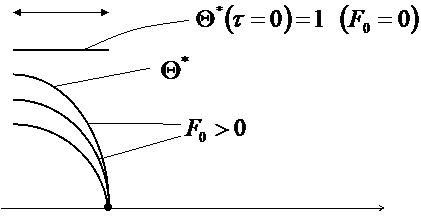
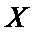
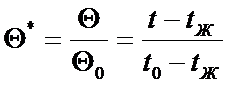
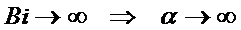
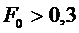 , мы получим:
, мы получим: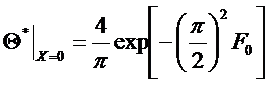 - температура на оси при больших временах.
- температура на оси при больших временах. через
через 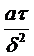 , мы получим:
, мы получим:
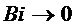

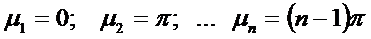
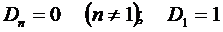
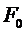 .
.
 при
при  :
:
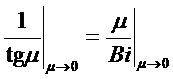

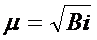







 :
: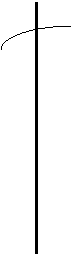

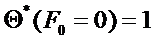

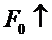



 .
.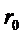 ,
,  . Цилиндр размещён в среде с постоянной
. Цилиндр размещён в среде с постоянной  , коэффициент теплоотдачи
, коэффициент теплоотдачи 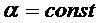 .
.

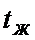
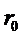
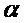
 Начальная температура в любой точке цилиндра
Начальная температура в любой точке цилиндра 


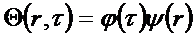

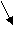




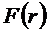


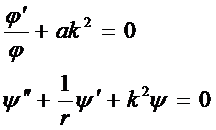

 - функция Бесселя первого рода нулевого порядка;
- функция Бесселя первого рода нулевого порядка;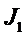 - функция Бесселя первого рода первого порядка.
- функция Бесселя первого рода первого порядка.
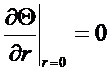 - условие симметрии.
- условие симметрии.


 - безразмерный радиус.
- безразмерный радиус.