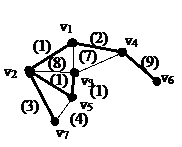G=(V,E) – неорграф
 - вершины графа
- вершины графа
V=VG, E=EG
Эксентреситет вершины Е графа G называется число E от v наибольшее из расстояний от этой вершины до остальных вершин E(v)=max(v,U) 
Рассмотрим r=r(G) граф G назыв наименьший из эксцентриситом его графов r=min E(v) 
Вершина эксцинтрисетет которой равен радиусу называется центральным
Диаметром графа D=D(G) называют наибольший из эксцентрисететов его вершин D(G)=maxE(v) 
Вершина эксцент. Который равен диаметру графа назыв переферийной

| I
| E(vi)
|
| 1
| 4
|
| 2
| 3
|
| 3
| 3
|
| 4
| 3
|
| 5
| 5
|
| 6
| 4
|
| 7
| 5
|
| R(G)
| 3
|
| D(G)
| 5
|
| C=
| {v2,v3,v4}
|

замечание во всяком полном графе r=D
Вершинная и реберная связанность графа.
Рассмотрим два связных графа

нетрудно видеть что степень связанности у этих графоф разная введем характеристики описывающие
числом вершиносвязанности  графа G назовем наименьшее число вершин удаления которых проводит к несвязанному или одновершинному графу
графа G назовем наименьшее число вершин удаления которых проводит к несвязанному или одновершинному графу 

введем сл обозначения: если имеет граф G то будем обозначать G-v-граф полученный удалением вершины v вместе с энцедентными ее ребрами
вершина v в связанном графе G называется точкой сочленения если граф G-v становится несвязанным

число  назыв числом реберной связанности граф G если графа при удалении
назыв числом реберной связанности граф G если графа при удалении  ребе (
ребе ( - минимальное число) становится несвязным (или увеличевается число несвязных компонентов)
- минимальное число) становится несвязным (или увеличевается число несвязных компонентов)



Вершинная реберная связь
Задача о компьютерах сетях
рассмотрим сесь состоящую из нескольких центров хранения и переработки информации и каналов по которым передается информация при этом сущ два способа передачи информации:
I. по началу соеденим два центра
II. через другие центры и каналы их соединяющим
Главная характеристика – ее надежность эта характеристика связанна со способностью функционирования при выходе из строя каких либо центров и каналов.
Такой сети можно поставить в соответствие граф.
Вершины- центры.
Ребра – каналы
Очевидно тенденция надежности является та сеть у которой числа вершин – реберной связанности выше.
Очевидно наиболее уязвимыми учаскамим в цепи будут те которые в графе соответствует мостам и точкам сочленения
Мостом называется ребро удленения которого приводит к увеличению числа связных компонентов.
Т.1(Уитни)/ для любого графа G верны неравенства

Док-во:
I. Докажем что 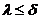
1-й случай: G ребер нет А=0 
2-й случай: G 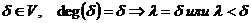
т.е. 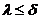
II. Докажем что 
1-й случай:G – не является связным 
2-й случай: G – связен и имеет мост
очевидно 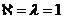
 выполняется
выполняется
3-й случай: G – связен и не имеет моста

из вершин инцидентных ребрам из множества E2 выберем те которые не совпадают с концами ребра ходящего в E2
удалим из G эти  вершин:
вершин:
a) Граф стал не связанным 
b) Граф остался связанным но теперь он имеет мост UV удалим вершину U т.е. граф стал несвязным: тогда 
§3 Деревья и их свойства.
Деревом называется связный граф не содержащий циклов
Произвольный ациклический граф называется лесом
Т.1(о весячей вершине)/ во всяком конечном дереве с числом вершин n>1 существует висячая вершина.
Док-во: Т-дерево;
Найдется вершина v степени 
Возьмем произвольную вершину дерева
Случай 1: v – висячая
Случай 2: v –не висячая 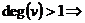 к этой вершине будет смежная с вершинной v. т.е. vv` не
к этой вершине будет смежная с вершинной v. т.е. vv` не 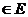
Рассмотрим вершину v`
v`` и т д
т.к. граф цикла не имеет то каждый раз происходит переход в новую нерассматриваемую вершину т.к. граф конечен то и просмотр вершин конечен то рано или поздно попадет висячая вершина.
Чтд
Двигаясь от вершины v в обратном направлении находим хотя бы еще одну висячую вершину.
Пусть G=(V,E) – это (n,m) –граф
Т.2/ для (n,m) графа следующ утверждения эквивалентны:
1. G-дерево
2. G – связный граф и m=n-1
3. G – ациклический граф и m=n-1
4. любые два несовпадающие вершины графа G соединят единственная простая цепь.
5. G- ациклический граф обладающий некоторыми свойствами что если любые две не смежные вершины соеденить ребром то получ граф имеет ровно один цикл.
Док –во:
1à 2 док во от противного
дано: G- дерево
док-ть: m=n-1
воспользуемся теоремой о висячей вершине пусть висячей вершиной является вершина v
будем выполнять просмотр дерева начиная с висячей вершины v, при просмотре добовляем каждый раз одно ребро и одну вершину т.к. циклов нет вершины каждый раз разные выполнив просмотр всего дерева получаем 
чтд
2à 3 дано G – связен m=n-1 док-ть: G – не имеет циклов
док-во:
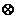 случай первый k<n вершин содержит цикл который содержит цикл
случай первый k<n вершин содержит цикл который содержит цикл
вне цикла: n-k вершин и n-k ребер
всего ребер: k(n-k)=n
т.е. m=n-1 не выполняется т.е. противоречит
случий 2 k=n n=m –ребер входит в цикл а это противоречит условию: m=n-1
чтд
3 à 4 дано: G ациклический и m=n-1докозать: любые две не совпадающие вершины соединяет единственная простая чепь.
Док-во:
Докажем что цепь единственна
Чтобы докозать что такая цепь существует надо док-ть что граф связан
К- связный компонент
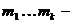 Кол-во ребер
Кол-во ребер 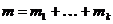
 кол-во вершин
кол-во вершин 
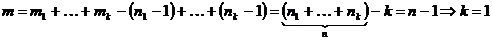
граф имеет к=1 связный компонент т.е. связен
чтд
4à 5
дано: граф G, две вершины.
доказать: если любые две не смежные вершины соеденить ребром то получ граф имеет ровно один цикл.
док-во:
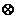 пусть граф G имеет цикл => найдется две вершины соеденяемые по меньшей мере двумя простыми цепями это противоречит условию => циклов в графе нету соеденим вершины u и v ребром по условию они соеденены цепью => получим цикл не трудно видеть этот цикл будет единственным т.к. убрав ребро мы получили бы что в графе еще есть ребра но граф ациклический.
пусть граф G имеет цикл => найдется две вершины соеденяемые по меньшей мере двумя простыми цепями это противоречит условию => циклов в графе нету соеденим вершины u и v ребром по условию они соеденены цепью => получим цикл не трудно видеть этот цикл будет единственным т.к. убрав ребро мы получили бы что в графе еще есть ребра но граф ациклический.
5 à дано: G- ациклич если любые 2 не смежные вершины соединить ребром то получается равно 1 цикл
док-ть: G-дерево
т.е. требуется док-ть связность графа
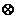 k>1
k>1
возьмем две вершины и соеденим их ребром но не получим цикла
чтд
Остов графа
G=(V,E) пусть Н – суграф графа G суграф Н называют остовым графом G если на каждом связном компоненте порождается дерево
В случае связного графа G остов называют каркасом покрывающим деревом или стягивающим графом
G=(V,E) – это (n,m) – граф
Т.(о циклическом ранге)/
Число ребер которые необходимо удалить в произвольном графе G для получения остова не зависит от последовательности их удаления и равно 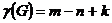 где k – число связанных компонентов.
где k – число связанных компонентов.
(m- число ребер n- число вершин)
Док – во:
а) G – связен тогда k=1 тогда остов есть дерево которое будет содержать n вершин и n-1 ребер тогда m-(n-1)= m-n+1= 
б) G – не связен имеет k>1 связных компонетов => mi – кол-во ребер в i связный компоненте ni – кол-во вершин => 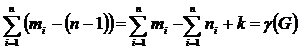
чтд.
Свойство дерева
1. Циклический ранг любого дерева равен нулю. Число  - циклич ранг или цикломатическое число.
- циклич ранг или цикломатическое число.
Т.(о центре дерева)/ Центр любого дерева состоит из одной вершины или двух смежных вершин
Док-во:
G=(V,E) – это (n,n-1) – граф(дерево)
Случай 1 n=1
●- это граф вершина.
центр состоит из одной вершины
теорема выполняется
Случай 2 n=2
 - это граф звено
- это граф звено
в этом случае центр состоит из двух вершин
Случай 3 n>2
По теореме о висячей вершине в дереве есть хотя бы одна висячая вершина. Удалим в дереве все висячие вершины вместе с инцидентными ребрами.
Не трудно видеть что в полученном дереве эксцентриситеты оставшихся вершин уменьшается на единицу. И соотношение между эксцентриситетами сохранится. Центр останется таким же как в исходном графе.
Процесс удаления всяческих вершин пока не останется одна вершина или две вершины соединенные ребром тогда все сводится к первому или второму случаю. Т.е. центр состоит из одной вершины или двух смежных.
Чтд
Т.(Кэли)/ Число помеченных деревьев порядка n равно 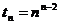 (Кэли для доказательства использовал отобрадение функций) (Кергофпри док-ве этой теоремы использовал последовательности для чисел от 1 до n из множества
(Кэли для доказательства использовал отобрадение функций) (Кергофпри док-ве этой теоремы использовал последовательности для чисел от 1 до n из множества  причем числа могли повторятся.)
причем числа могли повторятся.)
Док- во:
Подсчитаем число различных таких последовательностей.
n – способов поставить на первое место любое число столькоже на второе и тд

Док – во Прюфера:
Далее доказывается взаимнооднозначное соответствие м/у последовательностями указанного вида и помеченными деревьями.
Имеется дерево Т пометим его вершины от 1 до n
Выберем в дереве вершину с наименьшим номером пусть это b1 с ней смежная некоторая
вершина а1 Возьмем ребро e1=b1a1 и рассмотрим дерево Т-e1 полученное дерево обозначим Т1 В этом дереве проделываем ту же процедуру выбор вершины с наименьшим номером и т д продолжая процедуру получим:

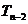 - две вершины соединенных ребром выпишем:
- две вершины соединенных ребром выпишем: 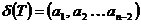 Каждому дереву (помеченному) соответствует единственная числовая последовательность построенная таким образом для каждой послед n-2 соответствует единичное дерево.
Каждому дереву (помеченному) соответствует единственная числовая последовательность построенная таким образом для каждой послед n-2 соответствует единичное дерево.
Чтд
Ориентированное дерево.
 А- предок
А- предок
B…K – потомки вершины А
С,В – непосредственный потомок вершины А(сын)
D,E,F – сын для В
В – непосредственный предок
F для К непосредственный отец
О./ Ориентированный деревом называется симметрический орентированный граф G(V,E)
В катором одна вершина 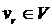 не имеет предков а все остальные вершины имеют только по одному непосредственному предку. Вершины
не имеет предков а все остальные вершины имеют только по одному непосредственному предку. Вершины 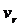 называется корнем дерева
называется корнем дерева
Бинарным деревом называется ордерево в котором каждая вершина имеет не более двух непосредственных потомков.
Полным бинарным деровом называется бинарн дерево в котором каждая вершина не является листом(лист-висячая вершина дерева) имеет ровно два непосредственных потомка.
Взвешенный граф
В реальный задачах часто приходится использовать дополнительную информацию (стоимость проезда расстояние между объектами электроники и т д)
 это (n,m)-граф
это (n,m)-граф
Взвешанным графом назыв пару (G,W) где G-граф а W-функция которая каждому ребру  ставит в соотношение число
ставит в соотношение число 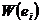 - называемое весом ребра
- называемое весом ребра 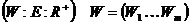 где
где 
Весом графа называют суммарный вес его ребер 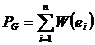
Рассмотрим связный неор граф остов лин веса тогда, остовом является суграф являющийся деревом Для данного взвешенного графа нужно найти остов минимального веса что: 
Применяется для проектирование дорог создание электроники.
1. Выберем  - ребро минимального строим дерево Т1(2 вершины a и bи ребро)
- ребро минимального строим дерево Т1(2 вершины a и bи ребро)
2. На некотором шаге имеем дерева Тk (имеем k+1 вершин) если k+1<n то среди ребер один конец принадлежит Тk а другой не принадлежит Тk выбирается ребро наименьшего веса, если же k+1=n то остов по строению.
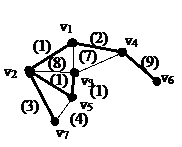
| i
| ei
| W(ei)
|
| 1
| 2.5
| 1
|
| 2
| 2.1
| 1
|
| 3
| 5.3
| 1
|
| 4
| 1.4
| 2
|
| 5
| 2.7
| 3
|
| 6
| 4.6
| 9
|
|
| Ростов=17
|
|
| | | | | |
Обходы
Эйлеровы графы
эйлеровым циклом в графе назыв цикл содержащий ребро графа в точности один раз.
Связный граф имеющий эйлеровый цикл назыв эйлеровым графом
Т./ Связный граф назыв эйлеровым когда степени его вершин четные.
Док – во: (необходимость)
граф Эйлера содержится эйлеровый цикл. Цикл проходя по некоторому ребру и входит в некоторую вершину и выходит по другому ребру поэтому каждой вершине транцидентно четное число ребер => число степени вершин четная
(достаточность)
Возьмем вершину v1 и начнем строить цикл
Случай 1 цикл включает в себя все ребра – эйлеров цикл
Случай 2 в цикл вошли не все ребра тогда среди вершин этого цикла найдется еще одна вершина которой транцидентны другие ребра пусть это вершина v2 у вершины v2 начнем строить цикл затем случай 1
Большой цикл включает все ребра => цикл эйлеров
продолжая этот процесс построения циклов и обьединение их в один цикл получим цикл включающий все ребра => цикл Эйлера
чтд



 - вершины графа
- вершины графа



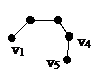

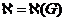 графа G назовем наименьшее число вершин удаления которых проводит к несвязанному или одновершинному графу
графа G назовем наименьшее число вершин удаления которых проводит к несвязанному или одновершинному графу 


 назыв числом реберной связанности граф G если графа при удалении
назыв числом реберной связанности граф G если графа при удалении  ребе (
ребе (


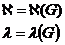

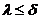

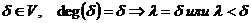


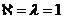

 вершин:
вершин:

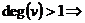 к этой вершине будет смежная с вершинной v. т.е. vv` не
к этой вершине будет смежная с вершинной v. т.е. vv` не 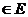

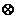 случай первый k<n вершин содержит цикл который содержит цикл
случай первый k<n вершин содержит цикл который содержит цикл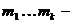 Кол-во ребер
Кол-во ребер 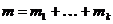
 кол-во вершин
кол-во вершин 
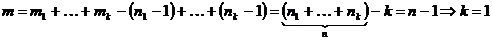
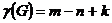 где k – число связанных компонентов.
где k – число связанных компонентов.
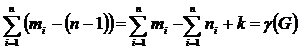
 - это граф звено
- это граф звено (Кэли для доказательства использовал отобрадение функций) (Кергофпри док-ве этой теоремы использовал последовательности для чисел от 1 до n из множества
(Кэли для доказательства использовал отобрадение функций) (Кергофпри док-ве этой теоремы использовал последовательности для чисел от 1 до n из множества  причем числа могли повторятся.)
причем числа могли повторятся.)


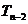 - две вершины соединенных ребром выпишем:
- две вершины соединенных ребром выпишем: 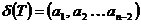 Каждому дереву (помеченному) соответствует единственная числовая последовательность построенная таким образом для каждой послед n-2 соответствует единичное дерево.
Каждому дереву (помеченному) соответствует единственная числовая последовательность построенная таким образом для каждой послед n-2 соответствует единичное дерево. А- предок
А- предок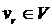 не имеет предков а все остальные вершины имеют только по одному непосредственному предку. Вершины
не имеет предков а все остальные вершины имеют только по одному непосредственному предку. Вершины 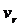 называется корнем дерева
называется корнем дерева это (n,m)-граф
это (n,m)-граф ставит в соотношение число
ставит в соотношение число 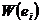 - называемое весом ребра
- называемое весом ребра 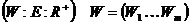 где
где 
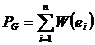

 - ребро минимального строим дерево Т1(2 вершины a и bи ребро)
- ребро минимального строим дерево Т1(2 вершины a и bи ребро)