Раздел I
Основные понятия теории множеств
О/под множеством будем понимать объединение в единое целое определенных вполне различных объектов называемых элементами множества
М – некоторое множество
х- некоторый элемент (х принадлежит М) 
примеры 1,2,3,4
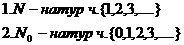
3. множество книжек на книжной полке:
а1,а2,а3,а4
4. множество точек отрезка прямой
равные множества. пустое множество. Подмножества
два множества А и В равны (А=В) если они состоят из одних и тех же эл
если А=В => если  и наоборот
и наоборот
 - пустое множество не имеющее элементов
- пустое множество не имеющее элементов
пусть А,В – множества причем каждый Эл множества А является Эл мн В говорят
 А включается в В, А –подмножество В если
А включается в В, А –подмножество В если  ,
,  то
то  (А- собств подмножество В)
(А- собств подмножество В)
Способы задания множеств
1) Пересечение (или список эл)
2) Порождающая процедура
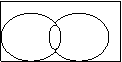
3) Диаграмма Эйлера-Венна
4) Аналитический (с помощью формулы)
1. пусть В – множество имеющее конечное число Эл т.е. конечное множество. Число Эл конечного множества называют мощностью множества и обоз. |В|
пример из пр3
|В|=4
В={ а1,а2,а3,а4}
2. пусть М – конечное множество х – произвольный Эл множества Н(х)свойство кат обладает каждый Эл множества М={х|Н(х)} или М={х: Н(х)}
пр5 М={х:х=2к, 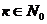 } 1,2,3,…..
} 1,2,3,…..
пр6 А={х:х=n2,  }1,4,9,…
}1,4,9,…
3.







Операции над множествами
1) Пересечение
2) Объединение
3) Дополнение
4) Разность
5) Симметрическая разность
1.  пересечением двух множеств А и В (
пересечением двух множеств А и В ( ) называют множества состоящие из всех тех и только тех Эл кат принадлежат и множеству А и множеству В
) называют множества состоящие из всех тех и только тех Эл кат принадлежат и множеству А и множеству В
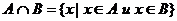
пр7 пусть А={a,b,d}
B={a,b,c,d,e}
 ={b,d}
={b,d}
A1  A2
A2  A3
A3  ….
….  An
An

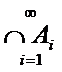
I- индекс 
Обьединением множество( ) называют множество сост. Из Эл принадлежащих хотябы одному из множеств А и В
) называют множество сост. Из Эл принадлежащих хотябы одному из множеств А и В
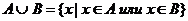
пр А={a,b,d}
B={b,c,d,e}
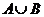 ={a,b,c,d,e}
={a,b,c,d,e}
A1  A2
A2  A3
A3  ….
….  An
An

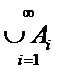
I-идекс 
Пусть имеется некоторое множество М выделим из этого множества подмножества следующим образом:
A1,A2,A3,….,An- множество М
1) 
2) 
каждый Эл поподает в одно и только одно подмножество
подмножества-блоки разбиения
совокупность A1,A2,A3,….,An- разбиение множества М
 О/ обьединение А и В таких х, что
О/ обьединение А и В таких х, что  называется свободным или дизюктивным
называется свободным или дизюктивным
3. пусть U некоторое множество А – его подмножество
дополнением (до U) множества А называют множество всех Эл 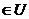 но
но  обозн
обозн 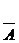

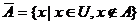
4.  разностью множеств А и В (А\В) называют множество всех тех и только тех Эл кат
разностью множеств А и В (А\В) называют множество всех тех и только тех Эл кат 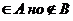

5. сим. разностью двух множеств А и В (обозА+В) называют множество всех Эл принадлежащих в точности только одному из множеств А и В.
Пр. U={a,b,c,d}
A={c}
 ={a,b,d}
={a,b,d}
пр.А и В из пр 7
свойства операций над множествами
1. 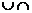
2. дополнение, 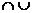

3. разность, 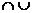

4. +

декартово произведение двух множеств
А,В – множество
Парой назовем символ (а,в)где  упорядоченный парой назовем множество{{a},{b}},
упорядоченный парой назовем множество{{a},{b}}, 
Декартовым произведением АхВ двух множеств А и В называется множество всех упорядоченных пар (а,в) где т.е. АхВ={(a,b):  }
}
декартово произведение n множеств
A1хA2хA3х….хAn-множеств А1,…, Аn называется множество A1хA2хA3х….хAn={(a1…an):a1 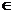 A1… an
A1… an 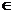 An} где символ (a1…an) называется последующий строка длинны n
An} где символ (a1…an) называется последующий строка длинны n
В частности если A1=A2=A3=….=An= A то декартово произведение Аn-n –ая декартова степень множества А
Функции
Мх и Му – некоторые множества
Мх х Му
Функцией F называется множество  такое что
такое что  найдется не более одного элемента
найдется не более одного элемента 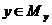 вида
вида  называется всюду определенной.
называется всюду определенной.
Отношения
n-мерным отношением R на непустом множестве А называется подмножества 
Если 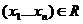 то говорят что отношение R выполняется для n элементов
то говорят что отношение R выполняется для n элементов 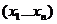 из множества А (обозначение
из множества А (обозначение 
Если 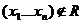 то говорят что отношение n не выполняется
то говорят что отношение n не выполняется
Тривиальный случай
1. R=Аn – полное или универсальное отношение  послед. Множество А выполняется отношение n
послед. Множество А выполняется отношение n
2.  не для каких n элементов
не для каких n элементов  не выполняется отношение n
не выполняется отношение n
3. n=1 – одноместное отношение В этом случае говорят о признаке которым обладает каждый элемент подмножества R множества А
4. n=2 – бинарное отношение
Бинарные отношения и их свойства
Пусть А некоторое множество квадратом множества А называется декартево произведение двух равных между собой множеств А и А; А х А=А2
Бинарным отношением на множестве А называются подмножество его квадратов
(обоз:  но чаще а R b)
но чаще а R b)
Пусть V-множество V2-квадрат этого множества пусть Е – бинарное отношение заданное на этом множестве совокупность множеств V с заданным на нем бинарным отношением называется графом  V-носитель графа(множество вершин) Е-сигнатура графа(мнодество дер.)
V-носитель графа(множество вершин) Е-сигнатура графа(мнодество дер.)
Способы задания бинарных отношений
1. перечислением
2. матрица
3. граф
4. фактор-множества
Свойства бинарных операций
А множество a,b,c –его элементы
1. рефлективность
2. антирефлективность
3. симметричность
4. антисимметричность
5. транзитивность
1. отношением R на множестве называется рефлективность если 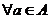 выполняется аRа
выполняется аRа
если рефлективное отношение задано матрицей то в ней на главной диагонали будут еденици
если задано графим то каждая вершина будет иметь петлю «Q»
2. отношением R на множестве называется антирефлективностью если не для каждого элемента выполняется аRа
в матрице описывающей антирефлективность на главной диогонале нет едениц
в графе нет петли
3. отношение R на множестве называется симметричным если для любых элементов  (если аRb то и bRa)
(если аRb то и bRa)
матрица описывающая симметричное отношение симметрична относительно главной диагонали
в графе две вершины соеденены дугой то они соеденены и противоположной дугой
4. отношением R на множестве называется антиимметричным если 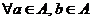 если аRb и bRa то а=b
если аRb и bRa то а=b
матрица описывающая антисимитричность не симметрична относительно диагонали
в графе нет пары дуг
5. отношением R на множестве называется транзитивным если  если aRb и bRc то аRс
если aRb и bRc то аRс
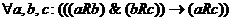
если задано графом то транзитивное замыкание
Отношение эквивалентности. Классы эквивалентности.
Отношение R на множестве А называется отношением эквивалентности если оно рефлексивно, симметрично, транзитивно.
Пусть имеется множество А на катором задано отношение эквивалентности R
Выполним сл построения
А R
 выделим из множества А все элементы множества С образуется С1
выделим из множества А все элементы множества С образуется С1
 и не вошедший в подмножество С1 аналогичным образом образец С2
и не вошедший в подмножество С1 аналогичным образом образец С2
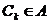
1. С1…Сk нет классов облодающих сл свойствами первая система планов есть разбиение те каждый элемент
2. любые два элемента принадлежащие одному классу эквивалентны
3. любые два элемента не пренадлежащие одному классу не эквивалентны
4. С1…Сk –класс эквивалентности
5. любой элемент принадлежащий некоторому классу эквивалентности называется его представителем
6. множество всех классов эквивалентно на множествое А называется фактором множеством множества А по эквивалентности R
Основы теории графов
Основные понятия и определения
1736 г Эйлер – Кёнигсбергские мосты
Граф – конфигурация из точек и соединяющих их линий (ввел - 1936 г.)
Пусть 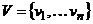 (непустое множество) обозначим через V2 – множество всех его двухэлементных подмножеств.
(непустое множество) обозначим через V2 – множество всех его двухэлементных подмножеств.
Графом G называется пара (V, E),где E – прямоугольное подмножество множества V2 
Если множество V конечно то граф конечен
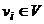 - вершина графов
- вершина графов
 - ребро графа
- ребро графа
 - элементы графа
- элементы графа
 -порядок графа (вершины)
-порядок графа (вершины)
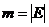 -ребра
-ребра
G – есть (n,m) – граф
V=VG ,E= EG
Две вершины U и V графа G называются смежными, если множество e = {u,v}является ребром.
Если e = {u,v} – есть ребро, то u и v концы ребра.
Два ребра называются смежными если они имеют общий конец.
Вершина v и ребро e графа G называются инцидентными если v является концом ребра e.
Вершина не инцидентна никакому ребру называется изолированной.
Множество всех вершин G смежных со всеми v называются окружениями вершины v и обозначаются N(v)
Граф G полным если любые две его вершины смежны.
Для полного (n,m) графа G число ребер 
Граф можно изобразить на бумаге при этом точкам ставятся соотношения вершины, а соединяющие их линии ребра.
Важно: при изображении графа является ли линии кривыми или прямыми, длинными или короткими, важно что линии соединяют две точки поэтому один и тот же граф может быть представлен различными чертежами.
Графы G1 и G2 изоморфные если существуют такое взаимоодназначное соответствие их вершин V1 и V2 что вершины в одном графе соединены рёбрами тогда и только тогда когда соответствующие им вершины соединяются ребрами в другом графе.
Ориентированный граф
G =(V,E) – это (n,m) – граф, e = a-b, e 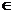 E –ребро графа
E –ребро графа
Если порядок расположения концов ребра не существенен, т.е. e = ab = ba, то говорят что e – не ориентир ребра, если порядок существенен, то e – ориентир ребра (дуга) e = ab ор. ребро.
a в начало и в конец дуги, говорят, что дуга выходит из вершины а и входит в конец в граф называется ориентированным если все его ребра ориентированны, не ориентированным если все его ребра не ориентированы.
 - обратный, получается путём изменения ориентации каждой дуги на противоположный
- обратный, получается путём изменения ориентации каждой дуги на противоположный
Соотнесенный неориентированный граф - получается из ориентир. графа путём отмены ориентации ребер.
Псевдо граф – это граф имеющий петли e=aa
Мульти граф имеющий так называемый кратным ребрами (пара вершин соединяется больше чем одним ребром)
Граф не имеющий петель и кратных ребер называют простым или обыкновенным.
Степенью вершины v графа G называют
1) число инцендентных ей ребер
2) число вершин ее окружения
3) число смежных с ней вершин
Вершина степени 1 называется висячей.
Граф называется однородным степени К(регулярным) если степени всех её вершин одинаковы и равны К.
Лемма: (о рукопожатиях)
Сумма степеней всех вершин графа G равна удвоенному числу ребер.
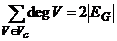
До-во: основано на том что каждое ребро имеет два конца и вносит в эту сумму двойку.
Теорема: Во всяком графе число вершин нечётной степени чётно.
Док-во: Выбросим из графа все нечётные степени то сумма остаётся чётной.
Граф Н называется частью графа G если VH 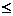 VG, EH
VG, EH 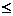 EG
EG
Часть Н графа G называется суграфом, если VH=VG
Помеченный граф
Помеченным графом G называются пара функций F: V →SV; 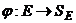 , 1 функция – функция распределения меток вершин,j -я функция распределения меток ребер.
, 1 функция – функция распределения меток вершин,j -я функция распределения меток ребер.
SV,SE – множество меток для вершин и ребер соответственно. Граф имеющий пометку называется помеченным графом.
Замечание. Граф может быть помеченным либо вершинами, либо ребрами.
Структуры данных для представленного графа.
1) Матрица смежности А
2) Матрица инцидентности В
3) Список ребер
Матрица смежности неорентир графа
G = (V,E) это (n,m) граф
Бинарная матрица смежности А графа G, называется матрица m´n где



Свойства матриц
1. матрицы симметричны относительно главной диагонали
2. количество элементов равно n2
3. если в вершине v2 имеется петля аij = 2
Матрица смежности А ориентир графа G называется бинарной матрицей размерности m´n

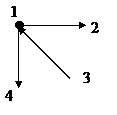 А=
А= 
2. Матрица инцидентности не ориентир графа
Матрица инцидентности В неорент графа G называется бинарная матрица m´n, если

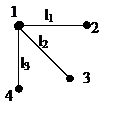 B=
B= 
Матрица инцидентности орентированного графа(орграфа)
М и В орграфа называются прямоугольная матрица nxm такая что



Список Ребер.
Связанный граф.
Связанные компоненты графа.
Пусть G=(V,E) –неорграф
Вершины графа - 
v,w графа G назыв связанным если существует маршрут с концами v и w
v и w – связанные вершины
нетрудно видеть: что если две вершины v, w – связанные то их соединяет простая цепь
Граф G связан если любая его пара вершин х в нем связана
Рассмотрим G=(V,E) – не связанный граф очевидно 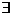 такое разложение множество его вершин на попарно пересекающиеся подмножества
такое разложение множество его вершин на попарно пересекающиеся подмножества 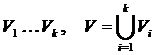 что все вершины в одном подмножестве связаны а вершины из различных подмножеств несвязан тогда граф G разлагается на непересекающиеся связные подграфы называемые связными компонентами графа
что все вершины в одном подмножестве связаны а вершины из различных подмножеств несвязан тогда граф G разлагается на непересекающиеся связные подграфы называемые связными компонентами графа 

Связный ациклический граф называется деревом
 длинна напр количеством в этом маршруте ребер(если некоторое ребро
длинна напр количеством в этом маршруте ребер(если некоторое ребро
повторяется более одного раза то оно учитывается)
Т.1/ Если в графе G равно две вершины имеют нечетную степень то эти вершины связаны.
Док-во:
Используем теорему о том что во всяком графе число вершин нечетной степени четно.
В случае связного графа это очевидно. Рассмотрим случай несвязанного – G U и v – вершины имеющие нечетную степень
Пусть вершина U попала в связную компоненту V1
Т.к. каждая связанная компонента графа тоже есть граф то вторая связная вершина поподает в V1
Чтд.
Расстояние в графе.
G=(V,E); U,v – вершины графа расстояние между U и v в графе G назыв наименьшая длинна простой цепи соеденяющей U и v
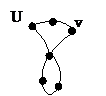
Обознач для расстояния d(U,v)
Для примера d(U,v)=2
Св - ва расстояний
1. 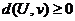 причем d(U,v)=0 тогда и только тогда когда U=v
причем d(U,v)=0 тогда и только тогда когда U=v
2. d(u,v)=d(v,U)
3. 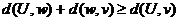
замечание: раст в орграфе можно рассматривать с учетом и без учета орентации
Вершинная реберная связь
Задача о компьютерах сетях
рассмотрим сесь состоящую из нескольких центров хранения и переработки информации и каналов по которым передается информация при этом сущ два способа передачи информации:
I. по началу соеденим два центра
II. через другие центры и каналы их соединяющим
Главная характеристика – ее надежность эта характеристика связанна со способностью функционирования при выходе из строя каких либо центров и каналов.
Такой сети можно поставить в соответствие граф.
Вершины- центры.
Ребра – каналы
Очевидно тенденция надежности является та сеть у которой числа вершин – реберной связанности выше.
Очевидно наиболее уязвимыми учаскамим в цепи будут те которые в графе соответствует мостам и точкам сочленения
Мостом называется ребро удленения которого приводит к увеличению числа связных компонентов.
Т.1(Уитни)/ для любого графа G верны неравенства

Док-во:
I. Докажем что 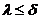
1-й случай: G ребер нет А=0 
2-й случай: G 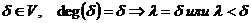
т.е. 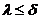
II. Докажем что 
1-й случай:G – не является связным 
2-й случай: G – связен и имеет мост
очевидно 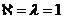
 выполняется
выполняется
3-й случай: G – связен и не имеет моста

из вершин инцидентных ребрам из множества E2 выберем те которые не совпадают с концами ребра ходящего в E2
удалим из G эти  вершин:
вершин:
a) Граф стал не связанным 
b) Граф остался связанным но теперь он имеет мост UV удалим вершину U т.е. граф стал несвязным: тогда 
§3 Деревья и их свойства.
Деревом называется связный граф не содержащий циклов
Произвольный ациклический граф называется лесом
Т.1(о весячей вершине)/ во всяком конечном дереве с числом вершин n>1 существует висячая вершина.
Док-во: Т-дерево;
Найдется вершина v степени 
Возьмем произвольную вершину дерева
Случай 1: v – висячая
Случай 2: v –не висячая 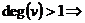 к этой вершине будет смежная с вершинной v. т.е. vv` не
к этой вершине будет смежная с вершинной v. т.е. vv` не 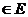
Рассмотрим вершину v`
v`` и т д
т.к. граф цикла не имеет то каждый раз происходит переход в новую нерассматриваемую вершину т.к. граф конечен то и просмотр вершин конечен то рано или поздно попадет висячая вершина.
Чтд
Двигаясь от вершины v в обратном направлении находим хотя бы еще одну висячую вершину.
Пусть G=(V,E) – это (n,m) –граф
Т.2/ для (n,m) графа следующ утверждения эквивалентны:
1. G-дерево
2. G – связный граф и m=n-1
3. G – ациклический граф и m=n-1
4. любые два несовпадающие вершины графа G соединят единственная простая цепь.
5. G- ациклический граф обладающий некоторыми свойствами что если любые две не смежные вершины соеденить ребром то получ граф имеет ровно один цикл.
Док –во:
1à 2 док во от противного
дано: G- дерево
док-ть: m=n-1
воспользуемся теоремой о висячей вершине пусть висячей вершиной является вершина v
будем выполнять просмотр дерева начиная с висячей вершины v, при просмотре добовляем каждый раз одно ребро и одну вершину т.к. циклов нет вершины каждый раз разные выполнив просмотр всего дерева получаем 
чтд
2à 3 дано G – связен m=n-1 док-ть: G – не имеет циклов
док-во:
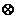 случай первый k<n вершин содержит цикл который содержит цикл
случай первый k<n вершин содержит цикл который содержит цикл
вне цикла: n-k вершин и n-k ребер
всего ребер: k(n-k)=n
т.е. m=n-1 не выполняется т.е. противоречит
случий 2 k=n n=m –ребер входит в цикл а это противоречит условию: m=n-1
чтд
3 à 4 дано: G ациклический и m=n-1докозать: любые две не совпадающие вершины соединяет единственная простая чепь.
Док-во:
Докажем что цепь единственна
Чтобы докозать что такая цепь существует надо док-ть что граф связан
К- связный компонент
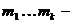 Кол-во ребер
Кол-во ребер 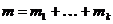
 кол-во вершин
кол-во вершин 
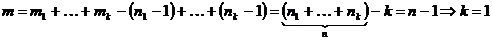
граф имеет к=1 связный компонент т.е. связен
чтд
4à 5
дано: граф G, две вершины.
доказать: если любые две не смежные вершины соеденить ребром то получ граф имеет ровно один цикл.
док-во:
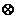 пусть граф G имеет цикл => найдется две вершины соеденяемые по меньшей мере двумя простыми цепями это противоречит условию => циклов в графе нету соеденим вершины u и v ребром по условию они соеденены цепью => получим цикл не трудно видеть этот цикл будет единственным т.к. убрав ребро мы получили бы что в графе еще есть ребра но граф ациклический.
пусть граф G имеет цикл => найдется две вершины соеденяемые по меньшей мере двумя простыми цепями это противоречит условию => циклов в графе нету соеденим вершины u и v ребром по условию они соеденены цепью => получим цикл не трудно видеть этот цикл будет единственным т.к. убрав ребро мы получили бы что в графе еще есть ребра но граф ациклический.
5 à дано: G- ациклич если любые 2 не смежные вершины соединить ребром то получается равно 1 цикл
док-ть: G-дерево
т.е. требуется док-ть связность графа
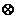 k>1
k>1
возьмем две вершины и соеденим их ребром но не получим цикла
чтд
Остов графа
G=(V,E) пусть Н – суграф графа G суграф Н называют остовым графом G если на каждом связном компоненте порождается дерево
В случае связного графа G остов называют каркасом покрывающим деревом или стягивающим графом
G=(V,E) – это (n,m) – граф
Т.(о циклическом ранге)/
Число ребер которые необходимо удалить в произвольном графе G для получения остова не зависит от последовательности их удаления и равно 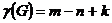 где k – число связанных компонентов.
где k – число связанных компонентов.
(m- число ребер n- число вершин)
Док – во:
а) G – связен тогда k=1 тогда остов есть дерево которое будет содержать n вершин и n-1 ребер тогда m-(n-1)= m-n+1= 
б) G – не связен имеет k>1 связных компонетов => mi – кол-во ребер в i связный компоненте ni – кол-во вершин => 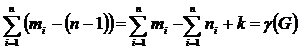
чтд.
Свойство дерева
1. Циклический ранг любого дерева равен нулю. Число  - циклич ранг или цикломатическое число.
- циклич ранг или цикломатическое число.
Т.(о центре дерева)/ Центр любого дерева состоит из одной вершины или двух смежных вершин
Док-во:
G=(V,E) – это (n,n-1) – граф(дерево)
Случай 1 n=1
●- это граф вершина.
центр состоит из одной вершины
теорема выполняется
Случай 2 n=2
 - это граф звено
- это граф звено
в этом случае центр состоит из двух вершин
Случай 3 n>2
По теореме о висячей вершине в дереве есть хотя бы одна висячая вершина. Удалим в дереве все висячие вершины вместе с инцидентными ребрами.
Не трудно видеть что в полученном дереве эксцентриситеты оставшихся вершин уменьшается на единицу. И соотношение между эксцентриситетами сохранится. Центр останется таким же как в исходном графе.
Процесс удаления всяческих вершин пока не останется одна вершина или две вершины соединенные ребром тогда все сводится к первому или второму случаю. Т.е. центр состоит из одной вершины или двух смежных.
Чтд
Т.(Кэли)/ Число помеченных деревьев порядка n равно 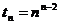 (Кэли для доказательства использовал отобрадение функций) (Кергофпри док-ве этой теоремы использовал последовательности для чисел от 1 до n из множества
(Кэли для доказательства использовал отобрадение функций) (Кергофпри док-ве этой теоремы использовал последовательности для чисел от 1 до n из множества  причем числа могли повторятся.)
причем числа могли повторятся.)
Док- во:
Подсчитаем число различных таких последовательностей.
n – способов поставить на первое место любое число столькоже на второе и тд

Док – во Прюфера:
Далее доказывается взаимнооднозначное соответствие м/у последовательностями указанного вида и помеченными деревьями.
Имеется дерево Т пометим его вершины от 1 до n
Выберем в дереве вершину с наименьшим номером пусть это b1 с ней смежная некоторая
вершина а1 Возьмем ребро e1=b1a1 и рассмотрим дерево Т-e1 полученное дерево обозначим Т1 В этом дереве проделываем ту же процедуру выбор вершины с наименьшим номером и т д продолжая процедуру получим:

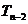 - две вершины соединенных ребром выпишем:
- две вершины соединенных ребром выпишем: 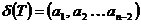 Каждому дереву (помеченному) соответствует единственная числовая последовательность построенная таким образом для каждой послед n-2 соответствует единичное дерево.
Каждому дереву (помеченному) соответствует единственная числовая последовательность построенная таким образом для каждой послед n-2 соответствует единичное дерево.
Чтд
Ориентированное дерево.
 А- предок
А- предок
B…K – потомки вершины А
С,В – непосредственный потомок вершины А(сын)
D,E,F – сын для В
В – непосредственный предок
F для К непосредственный отец
О./ Ориентированный деревом называется симметрический орентированный граф G(V,E)
В катором одна вершина 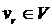 не имеет предков а все остальные вершины имеют только по одному непосредственному предку. Вершины
не имеет предков а все остальные вершины имеют только по одному непосредственному предку. Вершины 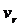 называется корнем дерева
называется корнем дерева
Бинарным деревом называется ордерево в котором каждая вершина имеет не более двух непосредственных потомков.
Полным бинарным деровом называется бинарн дерево в котором каждая вершина не является листом(лист-висячая вершина дерева) имеет ровно два непосредственных потомка.
Взвешенный граф
В реальный задачах часто приходится использовать дополнительную информацию (стоимость проезда расстояние между объектами электроники и т д)
 это (n,m)-граф
это (n,m)-граф
Взвешанным графом назыв пару (G,W) где G-граф а W-функция которая каждому ребру  ставит в соотношение число
ставит в соотношение число 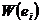 - называемое весом ребра
- называемое весом ребра 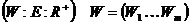 где
где 
Весом графа называют суммарный вес его ребер 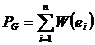
Рассмотрим связный неор граф остов лин веса тогда, остовом является суграф являющийся деревом Для данного взвешенного графа нужно найти остов минимального веса что: 
Применяется для проектирование дорог создание электроники.
1. Выберем  - ребро минимального строим дерево Т1(2 вершины a и bи ребро)
- ребро минимального строим дерево Т1(2 вершины a и bи ребро)
2. На некотором шаге имеем дерева Тk (имеем k+1 вершин) если k+1<n то среди ребер один конец принадлежит Тk а другой не принадлежит Тk выбирается ребро наименьшего веса, если же k+1=n то остов по строению.
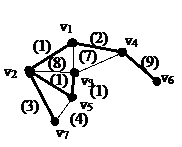
| i
| ei
| W(ei)
|
| 1
| 2.5
| 1
|
| 2
| 2.1
| 1
|
| 3
| 5.3
| 1
|
| 4
| 1.4
| 2
|
| 5
| 2.7
| 3
|
| 6
| 4.6
| 9
|
|
| Ростов=17
|
|
| | | | | |
Обходы
Эйлеровы графы
эйлеровым циклом в графе назыв цикл содержащий ребро графа в точности один раз.
Связный граф имеющий эйлеровый цикл назыв эйлеровым графом
Т./ Связный граф назыв эйлеровым когда степени его вершин четные.
Док – во: (необходимость)
граф Эйлера содержится эйлеровый цикл. Цикл проходя по некоторому ребру и входит в некоторую вершину и выходит по другому ребру поэтому каждой вершине транцидентно четное число ребер => число степени вершин четная
(достаточность)
Возьмем вершину v1 и начнем строить цикл
Случай 1 цикл включает в себя все ребра – эйлеров цикл
Случай 2 в цикл вошли не все ребра тогда среди вершин этого цикла найдется еще одна вершина которой транцидентны другие ребра пусть это вершина v2 у вершины v2 начнем строить цикл затем случай 1
Большой цикл включает все ребра => цикл эйлеров
продолжая этот процесс построения циклов и обьединение их в один цикл получим цикл включающий все ребра => цикл Эйлера
чтд
Алгоритм Фиери.
G=(V,E)
Как занумировать ребра графа таким образом чтобы номер ребра указывал каким по счету это ребро проводится
Правило 1  присвоим ему номер 1 и вычеркнем.
присвоим ему номер 1 и вычеркнем.
Правило 2 Пусть пронумеровано и вычеркнуто k ребер, а W-вершина в которую пришли, тогда среди ребер инцидентных W и не вычеркнутых выбирается любое ребро, выбранному ребру присваивается номер ребра не пронумерованных и не вычеркнутых
Полуэйлеровый граф.
О./ Цепь содержащую все ребра графа в точности по одному разу назыв эйлеровой цепью
Связанный граф имеющий Эйлировы цепь называется полуэйлеровым графом
Т./ Граф G называется полуэйлеровым, тогда когда граф связан и число вершин нечетной степени равное 2.
Док – во: (необходимость)
Связность следует из определения эйлеровой цепи.
Пусть a – начало, а b-конец э.ц., степени остольных вершин должны быть четными, т.к. цепь ребер входящих в одну вершину выходит через др ребро. Причем из вершины а выходит цепь но не завершается в ней поэтому степень вершины а нечетна, аналогично цепь завершается и в вершине b но не начинается там, отсюда => степень b нечетна => в графе две вершины имеют нечетную степень
(достаточность)
Пусть вершины a,b имеют нечетную степень.
Сл 1 вершина a,b смежные, удалим ребро аb тогда получим число вершин четное, строим эйлеровый цикл добавим ребро получим эйлерову цепь
Сл 2 вершины a,b не смежены добавим ребро ab, степени всех вершин четны значит существует эйлерова цепь => строим эйлерову цепь. Удалим ребро аb степень вершин ab нечетна, получаем эйлеровый цикл
Гамельтоновый Граф
Гамельтоновым циклом называют простой цикл содержащий величену графа ровно один раз
граф имеющий Гамельтоновый цикл называется Гамельтоновым графом
Гамельтоновой цепью в графе назыв цепь проходящую через вершину графа 1 раз граф содержащий Гамельтонову цепь называют трассируемым задачи о комивоежоре в полном взвешенном графе G найти Гамельтоновый цикл(цепь наименьшего веса)
к этой задаче в частности сводится задача выборе последовательности заданий на комп(с предварительной настройкой)
для G графов не известно простое необходимое и достаточное условие существования Гамельтоновости, одна из центральных проблем в теории графов. не известен алгоритм который в проверенном графе, с использованием числа шагов ограничен полиномом от размерности задачи.
Проблема существование гамельтонового пути относится к числу № Р – полных задач
Грани плоского графа
Грани плоского графа G назыв часть плоскости ограниченная простым циклом м не содержащая внутри постых циклов каждый граф имеет внешнею грань и некоторое кол – во внутренних.
Границей грани назыв множество вершин и ребер принадлежащих этой грани.
Операция подразбиение ребра
 Пусть в графе G=(V,E)
Пусть в графе G=(V,E) 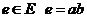 операция подразбиение ребра выполняется следующ образом: 1) ребро е удаляется вместо него вводится новая вершина с и ребра
операция подразбиение ребра выполняется следующ образом: 1) ребро е удаляется вместо него вводится новая вершина с и ребра 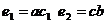

((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228268']=__lxGc__['s']['_228268']||{'b':{}})['b']['_697691']={'i':__lxGc__.b++};




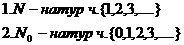
 и наоборот
и наоборот - пустое множество не имеющее элементов
- пустое множество не имеющее элементов А включается в В, А –подмножество В если
А включается в В, А –подмножество В если  то
то  (А- собств подмножество В)
(А- собств подмножество В)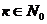 } 1,2,3,…..
} 1,2,3,….. }1,4,9,…
}1,4,9,…






 пересечением двух множеств А и В (
пересечением двух множеств А и В ( ) называют множества состоящие из всех тех и только тех Эл кат принадлежат и множеству А и множеству В
) называют множества состоящие из всех тех и только тех Эл кат принадлежат и множеству А и множеству В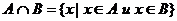
 A2
A2 

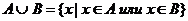
 ={a,b,c,d,e}
={a,b,c,d,e}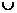 A2
A2 
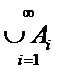



 О/ обьединение А и В таких х, что
О/ обьединение А и В таких х, что  называется свободным или дизюктивным
называется свободным или дизюктивным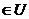 но
но  обозн
обозн 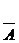

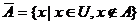
 разностью множеств А и В (А\В) называют множество всех тех и только тех Эл кат
разностью множеств А и В (А\В) называют множество всех тех и только тех Эл кат 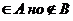

 ={a,b,d}
={a,b,d}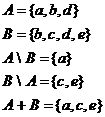
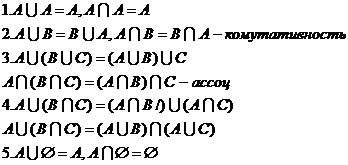



 упорядоченный парой назовем множество{{a},{b}},
упорядоченный парой назовем множество{{a},{b}},  A1… an
A1… an  такое что
такое что  найдется не более одного элемента
найдется не более одного элемента  вида
вида  называется всюду определенной.
называется всюду определенной.
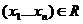 то говорят что отношение R выполняется для n элементов
то говорят что отношение R выполняется для n элементов 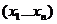 из множества А (обозначение
из множества А (обозначение 
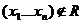 то говорят что отношение n не выполняется
то говорят что отношение n не выполняется послед. Множество А выполняется отношение n
послед. Множество А выполняется отношение n не для каких n элементов
не для каких n элементов  не выполняется отношение n
не выполняется отношение n но чаще а R b)
но чаще а R b) V-носитель графа(множество вершин) Е-сигнатура графа(мнодество дер.)
V-носитель графа(множество вершин) Е-сигнатура графа(мнодество дер.)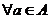 выполняется аRа
выполняется аRа  (если аRb то и bRa)
(если аRb то и bRa)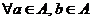 если аRb и bRa то а=b
если аRb и bRa то а=b если aRb и bRc то аRс
если aRb и bRc то аRс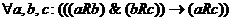
 выделим из множества А все элементы множества С образуется С1
выделим из множества А все элементы множества С образуется С1 и не вошедший в подмножество С1 аналогичным образом образец С2
и не вошедший в подмножество С1 аналогичным образом образец С2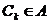
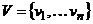 (непустое множество) обозначим через V2 – множество всех его двухэлементных подмножеств.
(непустое множество) обозначим через V2 – множество всех его двухэлементных подмножеств.
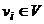 - вершина графов
- вершина графов - ребро графа
- ребро графа - элементы графа
- элементы графа -порядок графа (вершины)
-порядок графа (вершины)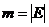 -ребра
-ребра
 - обратный, получается путём изменения ориентации каждой дуги на противоположный
- обратный, получается путём изменения ориентации каждой дуги на противоположный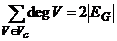
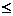 VG, EH
VG, EH 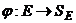 , 1 функция – функция распределения меток вершин,j -я функция распределения меток ребер.
, 1 функция – функция распределения меток вершин,j -я функция распределения меток ребер.



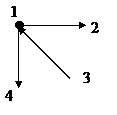 А=
А= 

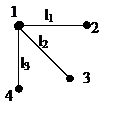 B=
B= 




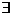 такое разложение множество его вершин на попарно пересекающиеся подмножества
такое разложение множество его вершин на попарно пересекающиеся подмножества 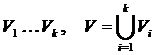 что все вершины в одном подмножестве связаны а вершины из различных подмножеств несвязан тогда граф G разлагается на непересекающиеся связные подграфы называемые связными компонентами графа
что все вершины в одном подмножестве связаны а вершины из различных подмножеств несвязан тогда граф G разлагается на непересекающиеся связные подграфы называемые связными компонентами графа 

 длинна напр количеством в этом маршруте ребер(если некоторое ребро
длинна напр количеством в этом маршруте ребер(если некоторое ребро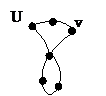
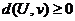 причем d(U,v)=0 тогда и только тогда когда U=v
причем d(U,v)=0 тогда и только тогда когда U=v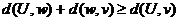
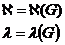

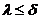

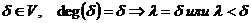


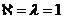

 вершин:
вершин:

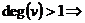 к этой вершине будет смежная с вершинной v. т.е. vv` не
к этой вершине будет смежная с вершинной v. т.е. vv` не 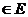

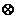 случай первый k<n вершин содержит цикл который содержит цикл
случай первый k<n вершин содержит цикл который содержит цикл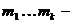 Кол-во ребер
Кол-во ребер 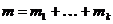
 кол-во вершин
кол-во вершин 
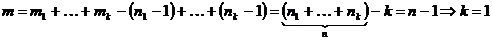
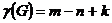 где k – число связанных компонентов.
где k – число связанных компонентов.
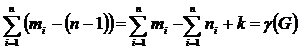
 - это граф звено
- это граф звено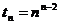 (Кэли для доказательства использовал отобрадение функций) (Кергофпри док-ве этой теоремы использовал последовательности для чисел от 1 до n из множества
(Кэли для доказательства использовал отобрадение функций) (Кергофпри док-ве этой теоремы использовал последовательности для чисел от 1 до n из множества  причем числа могли повторятся.)
причем числа могли повторятся.)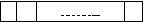


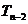 - две вершины соединенных ребром выпишем:
- две вершины соединенных ребром выпишем: 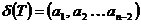 Каждому дереву (помеченному) соответствует единственная числовая последовательность построенная таким образом для каждой послед n-2 соответствует единичное дерево.
Каждому дереву (помеченному) соответствует единственная числовая последовательность построенная таким образом для каждой послед n-2 соответствует единичное дерево. А- предок
А- предок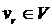 не имеет предков а все остальные вершины имеют только по одному непосредственному предку. Вершины
не имеет предков а все остальные вершины имеют только по одному непосредственному предку. Вершины 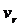 называется корнем дерева
называется корнем дерева это (n,m)-граф
это (n,m)-граф ставит в соотношение число
ставит в соотношение число 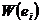 - называемое весом ребра
- называемое весом ребра 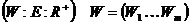 где
где 
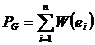

 - ребро минимального строим дерево Т1(2 вершины a и bи ребро)
- ребро минимального строим дерево Т1(2 вершины a и bи ребро)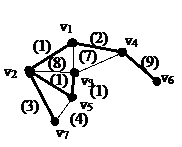
 присвоим ему номер 1 и вычеркнем.
присвоим ему номер 1 и вычеркнем. Пусть в графе G=(V,E)
Пусть в графе G=(V,E) 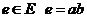 операция подразбиение ребра выполняется следующ образом: 1) ребро е удаляется вместо него вводится новая вершина с и ребра
операция подразбиение ребра выполняется следующ образом: 1) ребро е удаляется вместо него вводится новая вершина с и ребра