Знание точного смысла слов и, или, все, каждый.

Практическое занятие

 

Тема: «Формирование алгоритмического мышления младших

школьников».

План.

1.Обоснуйте взаимосвязь логического и алгоритмического мышления. Какие умения называют алгоритмическими? Назовите основные алгоритмические умения.

Умение последовательно, чётко и непротиворечиво излагать свои мысли, тесно связанные с умением представлять сложное действие в виде организованной последовательности простых действий называется алгоритмическим. Оно находит своё выражение в том, что человек, видя конечную цель, может составить алгоритмическое предписание или алгоритм (если он существует), в результате выполнения которого цель будет достигнута.

Под способностью алгоритмически мыслить понимается умение решать задачи различного происхождения, требующие составления плана действий для достижения желаемого результата.

Основной особенностью алгоритмического мышления считается умение определять последовательность действий (алгоритм), необходимую для решения поставленной задачи. Очевидно, что потребность в подобном умении возникла достаточно давно, однако до ХХ века алгоритмическое мышление не выделялось как отдельный тип мышления. Выделять алгоритмическое мышление в качестве отдельного типа мышления стали сравнительно недавно, толчком к чему, несомненно, послужило развитие вычислительной техники.

Основные логические структуры мышления формируются в возрасте 5-11 лет. Запоздалое формирование этих структур протекает с большими трудностями и часто остаётся незавершённым. Следовательно, обучать детей в этом направлении целесообразно с начальной школы.

Учёт этих возрастных особенностей позволяет успешно развивать у детей алгоритмическое мышление и творческие способности, поддерживать постоянный интерес к предмету, даёт возможность на высоком уровне изучать математику.

Задачей начального курса математики является формирование вычислительной культуры, развитие алгоритмического мышления и творческих способностей младших школьников. Алгоритмическое мышление на уроках математики развивается с помощью игр, сюжет которых основан на известных сказках; творческие способности учащихся развиваются посредством художественной деятельности, при подготовке и проведении викторин, конкурсов рисунков и т.п.

Алгоритмическое мышление, рассматриваемое как представление последовательности действий, наряду с образным и логическим мышлением определяет интеллектуальную мощь человека, его творческий потенциал. Навыки планирования, привычка к точному и полному описанию своих действий помогают школьникам разрабатывать алгоритмы решения задач самого разного происхождения.

Алгоритмическое мышление является необходимой частью научного взгляда на мир. В то же время оно включает и некоторые общие мыслительные навыки, полезные и в более широком контексте.

Алгоритмическое мышление включает в себя ряд особенностей, свойственных логическому мышлению, однако требует и некоторых дополнительных качеств. Основными из них считаются умение находить последовательность действий, необходимых для решения поставленной задачи, и выделение в общей задаче ряда более простых задач, решение которых приведёт к решению исходной задачи. Наличие логического мышления не обязательно (хотя и достаточно часто) предполагает наличие мышления алгоритмического.

На сегодняшний день одна из современных образовательных проблем - проблема «общения» с компьютерной техникой, требует умения понимать различного рода алгоритмические языки, а также наличия определённого уровня сформированности алгоритмического мышления. Отсюда и возникает задача формирования элементов алгоритмической грамотности уже в начальной школе. Большинство программ по математике начальной школы ориентировано на формирование логического и алгоритмического мышления, все они содержат раздел, посвящённый алгоритмам. Ведущая роль в решении сложившейся дидактической проблемы принадлежит учителю, который может организовать работу с алгоритмическими обучающими средствами на уроках математики, способствуя тем самым развитию алгоритмического мышления у младших школьников.

Формирования элементов алгоритмической грамотности, по мнению ведущих педагогов-методистов, должно осуществляться на основе логических знаний и умений учащихся. Так А.И. Газейкина выделяет следующие комплексы методических приёмов, применение которых способствует развитию алгоритмического мышления:

· Создание нового алгоритма, его запись, проверка и исполнение самим обучаемым или выбранным исполнителем.

· Усвоение алгоритмов решения основных типовых задач.

· Поиск и исправление синтаксических и семантических ошибок в алгоритме.

· Оптимизация готового алгоритма.

· Учитывая связи между элементами логической и алгоритмической грамотности, в начальном курсе математики представлен следующий план реализации единой логико-алгоритмической линии:

Логическая:

· Умение узнавать предмет по данным признакам.

· Умение сравнивать.

· Умение распределять предметы по определённым признакам группы.

· Умение устанавливать соотношения общего и частного.

· Понимание смысла слов: и, или, все, каждый, некоторые.

· Умение получать умозаключение.

· Умение обосновывать умозаключение.

· Умение составлять алгоритм.

· Умение проверять правильность алгоритма.

Алгоритмическая:

· Понимание сущности алгоритма, его свойств.

· Умение читать алгоритм.

· Умение четко исполнять алгоритм.

· Знакомство с основными типами алгоритмов.

· Умение преобразовывать алгоритм.

· Умение выбирать рациональный алгоритм.

Умение сравнивать.

Умение составлять алгоритм.

НУМЕРАЦИЯ

 

 

 

Алгоритм написания цифры 5:

 

 

АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ

 

ЗАДАЧИ

Алгоритм осмысления задачи:

1. Прочитай правильно задачу и поставь логическое ударение.

2. Представь ситуацию, описанную в задаче.

3. Разбей задачу на смысловые части.

4. Переформулируй текст задачи:

— замени термин содержательным описанием или замени содержательное описание терминами; — исключи части текста, не влияющие на результат решения;

— измени порядок слов и предложений, дополни текст пояснениями.

5. Построй модель.

Алгоритм решения задачи:

1. Прочитай задачу. Пойми и запомни ее условие и вопрос.

2. Ответь на вопросы: Что известно? Что надо узнать? Можно ли сформулировать задачу иначе, проще?

3. Выполни схематический рисунок (чертеж) к задаче.

4. Подумай, как можно найти неизвестное? Для этого:

а) вспомни нужное правило, формулы;

б) составь план решения задачи.

5. Запиши решение задачи по действиям (с пояснением) или выражением.

6. Проверь решение задачи. Подумай, правдоподобен ли результат; можно ли составить и решить обратную задачу; нельзя ли решить задачу другим способом, проще.

7. Сформулируй и запиши ответ задачи.

Алгоритм решения задачи на движение:

1. Прочитай текст задачи про себя.

2. Прочитай текст задачи вслух. Представь жизненную ситуацию, о ко‑ торой говорится в задаче. Ответь на вопросы:

О ком (чем) говорится в задаче?

Что говорится о направлении движения?

Что показывают числа?

Что нужно узнать в задаче?

3. Выполни иллюстрацию к задаче. Подумай, как обозначить на чертеже:

а) путь, расстояние;

б) направление движения;

в) место встречи? Выполни чертеж.

4. Повтори задачу по иллюстрации.

5. Составь план решения задачи.

6. Запиши решение задачи по действиям (с пояснением) или выражением.

7. Проверь ход и результат решения задачи. Возможны ли другие результаты решения?

8. Сформулируй и запиши ответ задачи.

 

ГЕОМЕТРИЧЕСКИЙ МАТЕРИАЛ

Алгоритм вычитания отрезков:

1) Начертить луч

2) Измерить при помощи циркуля отрезок первый

3) Отложить этот отрезок, выделить его “дугой”

4) Измерить второй отрезок

5) Построить второй отрезок начиная от начала луча, выделить его “дугой.”

6) Выделить оставшуюся часть – отрезок – это будет разностью отрезков

- При вычитании отрезков оба отрезка нужно построить на луче от его начала

План построения прямоугольника:

1) Построить произвольную прямую;

2) Отложить на ней нижнее основание;

3) Принимая его концы за вершины углов, с помощью чертежного треугольника построить прямые углы;

4) На сторонах этих углов от концов нижнего основания от­ложить боковые стороны;

5) Концы боковых сторон соединить отрезком.

 

План построения треугольника:

1) Провести произвольную прямую. Одна из данных сторон принимается за основание будущего треугольника.

2) Затем раствором циркуля равным второй стороне, из точки А как из центра проводится дуга, а раствором циркуля, равным третьей стороне из точки С как из центра проводится вторая дуга.

3) Точка пересечения дуг обозначается буквой В, точка В соединяется отрезками с точками А и С.

Алгоритм построения угла:

1) Начертить луч.

2) Совместить центр транспортира с началом луча так, чтобы луч проходил через начало отсчета на шкале транспортира.

3) Учитывая вид угла, найти на нужном ряду необходимое значение угла и поставить на бумаге точку.

4) Соединить начало луча с отмеченной точкой.

5) Проверить вид угла, который нужно построить. Искомый угол построен.

ВЕЛИЧИНЫ

АЛГЕБРАИЧЕСКИЙ МАТЕРИАЛ

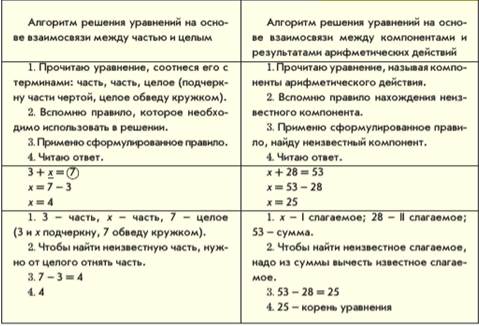
Алгоритм решения уравнений на нахождение неизвестной части через использование предметной иллюстрации

1) Прочитай компоненты уравнения, соотнеся их с понятиями: целое, часть, часть.

2) Зачеркни в целом известную часть.

3) Запиши оставшуюся часть.

I слагаемое – часть,

II слагаемое – часть,

сумма – целое.

 

Алгоритм может быть сформулирован в процессе изучения материала и служит базой для рассуждений при выполнении заданий данного типа.

Составим и решим уравнение, заданное в условиях, отличных от прежних.

Сформулируем алгоритм нахождения корня уравнения, основанный на способе графического моделирования.

Предложим вспомогательные и математические модели уравнений с использованием числового отрезка.

Для обсуждения способа нахождения корня уравнения предложим систему вопросов:

- С какого числа записано уравнение? Почему?

-  Когда в уравнении ставят знак «–», а когда «+»?

- Какое число записывают после знака «=»? Почему?

- Как найти корень уравнения, опираясь на числовой отрезок?

Осуществим план составления уравнения и нахождения его корня.

Алгоритм решения уравнения с помощью числового отрезка

1) Запишу число, от которого направлена стрелка.

2) Поставлю знак арифметического действия (если направление движения влево – «–», вправо – «+»).

3) Обозначу неизвестный компонент буквой х.

4) Запишу знак равенства и число, на котором завершено движение стрелки.

5) Посчитаю, сколько единиц между числами.

6) Запишу ответ.

 

Алгоритм решения уравнений на основе знаний конкретного смысла умножения

1) Заменю сумму одинаковых слагаемых действием умножения.

2) Сравню левую и правую части уравнения.

3) Сделаю вывод.

17 + 17 = 17 ∙ х

17 ∙ 2 = 17 ∙ х

2 = х

Алгоритм можно предлагать в различных формах.

1. Словесная запись предполагает описание последовательности выполнения действий на естественном языке. Например:

Алгоритм решения уравнений через взаимосвязь между компонентами и результатами арифметических действий в две ступени

1) Установлю, какое действие выполняется последним.

2) Установлю, чем выражены компоненты этого действия.

3) Вспомню и применю правило нахождения неизвестного компонента.

4) Преобразую правую часть уравнения.

5) Прочитаю полученное уравнение, называя компоненты.

6) Вспомню и применю правило нахождения неизвестного компонента.

7) Найду корень уравнения.

8) Проверю, сделаю вывод.

(х + 3): 8 = 5

х + 3 = 5 ∙ 8

х + 3 = 40

х = 40 – 3

х = 37

(37 + 3): 8 = 5

2 = 5

 

2. Запись, где алгоритм представлен в виде программы действий. Например:

Программа нахождения неизвестного уменьшаемого

(здесь под знаками     и  подразумеваются численные значения)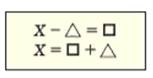

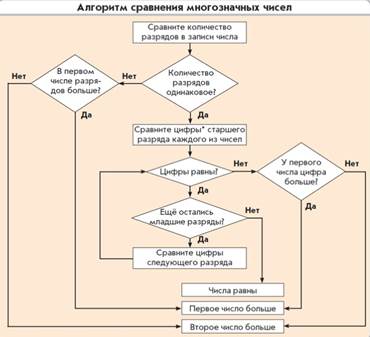
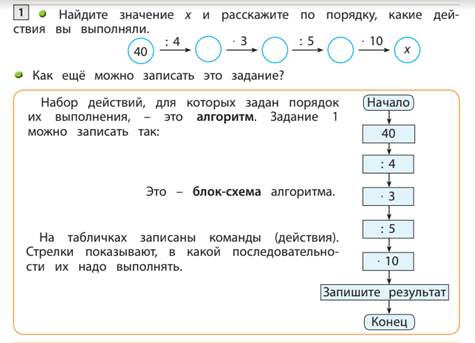
3. Запись алгоритма на языке блок-схем. Они состоят из блоков и стрелок, которые указывают последовательность выполнения действий. Например:

Алгоритм решения уравнений на основе части и целого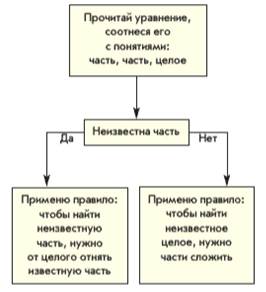

Основной целью обучения составлению алгоритмов и их использования на уроках математики в начальной школе является формирование у детей умения планировать свои действия, осуществлять поиск решения поставленной перед ними задачи. Одновременно дети осваивают соответствующий объём знаний, предусмотренный программой.

4.    Как сформировать умение младших школьников составлять  алгоритмические предписания? Приведите примеры различных упражнений с этой целью.

Составление алгоритмических предписаний (алгоритмов) – сложная задача, поэтому начальный курс математики не ставит своей целью её решение. Но определённую подготовку к её достижению он может и должен взять на себя, способствуя тем самым развитию логического мышления школьников.

Для этого, начиная с 1-го класса, нужно, прежде всего, учить детей «видеть» алгоритмы и осознавать алгоритмическую сущность тех действий, которые они выполняют. Начинать эту работу следует с простейших алгоритмов, доступных и понятных им.

Можно составить алгоритм перехода улицы с нерегулируемым и регулируемым перекрёстком, алгоритмы пользования различными бытовыми приборами, приготовления какого-либо блюда (рецепт приготовления), представить в виде последовательных операций путь от дома до школы, от школы до ближайшей остановки автобуса и т.д.

Способ приготовления кофейного напитка написан на коробке и представляет собой следующий алгоритм:

1. Налить стакан горячей воды в кастрюлю.

2. Взять чайную ложку напитка.

3. Засыпать (всыпать) кофейный напиток в кастрюлю с водой.

4. Нагреть содержимое кастрюли до кипения.

5. Дать напитку отстояться.

6. Налить напиток в стакан.

 

Рассматривая такие инструкции, сам термин «алгоритм» можно не вводить, а говорить о правилах, в которых выделены пункты, указывающие на определённые действия, в результате выполнения которых решается поставленная задача.

Следует заметить, что сам термин «алгоритм» можно употреблять только условно, так как те правила и предписания, которые рассматриваются в курсе математики начальных классов, не обладают всеми свойствами, его характеризующими.

Алгоритмы в начальных классах описывают последовательность действий на конкретном примере не в общем виде, в них находят отражение не все операции, входящие в состав выполняемых действий, поэтому их последовательность строго не определена. Например, последовательность действий при умножении чисел, оканчивающихся нулями, на однозначное число (800 ∙ 4) выполняется так:

1. Представим первый множитель в виде произведения однозначного числа и единицы, оканчивающейся нулями:

               (8 ∙ 100) ∙ 4.

2. Воспользуемся сочетательным свойством умножения:

             (8 ∙ 100) ∙ 4 = 8 ∙ (100 ∙ 4).

3. Воспользуемся переместительным свойством умножения:

8 ∙ (100 ∙ 4) = 8 ∙ (4 ∙ 100).

4.Воспользуемся сочетательным свойством умножения:

8 ∙ (4 ∙ 100) = (8 ∙ 4) ∙ 100.

5.Заменим произведение в скобках его значением:

             (8 ∙ 4) ∙ 100 = 32 ∙ 100.

1. При умножении числа на 1 с нулями нужно приписать к числу столько нулей, сколько их во втором множителе: 32 ∙ 100= 3200.

Безусловно, младшие школьники не могут усвоить последовательность действий в таком виде, но, представляя отчётливо все операции, учитель может предлагать детям различные упражнения, выполнение которых позволит детям осознать способ деятельности. Например:

Можно ли, не выполняя вычислений, утверждать, что значения выражений в каждом столбике одинаковы:

9 ∙ (8 ∙ 100)    800 ∙ 7

(9 ∙ 8) ∙ 100    (8 ∙ 7) ∙ 100

(9 ∙ 100) ∙ 8     8 ∙ (7 ∙ 100)

9∙ 100             8 ∙ 700

72 ∙ 100               56 ∙ 100

Объясни, как получено выражение, записанное справа:

8 ∙ 6 ∙ 10 = 40 ∙ 6 2 ∙ 8 ∙ 10 = 20 ∙ 8

8 ∙ 5 ∙ 10 = 8 ∙ 50 5 ∙ 7 ∙ 10 = 7 ∙ 50

Можно ли утверждать, что значения произведений в каждой паре одинаковы:

45 ∙ 10  54 ∙ 10    32 ∙ 10

9 ∙ 50       60 ∙ 9        8 ∙ 40

Для осознания детьми алгоритмической сути выполняемых ими действий нужно переформулировать данные математические задания в виде определённой программы.

Например, задание «найти 5 чисел, первое из которых равно 3, каждое следующее на 2 больше предыдущего» можно представить в виде алгоритмического предписания так:

2. Запиши число 3.

3. Увеличь его на 2.

4. Полученный результат увеличь на 2.

5. Повторяй операцию 3 до тех пор, пока не запишешь 5 чисел.

Словесное алгоритмическое предписание можно заменить схематическим:

Это позволит учащимся более чётко представить каждую операцию и последовательность их выполнения.

Наряду со словесными и схематическими предписаниями можно задать алгоритм в виде таблицы.

Например, задание: «Запиши числа от 1 до 6. Каждое увеличь: а) на 2; б) на 3» можно представить в такой таблице:

+	1	2	3	4	5	6
2
3

Таким образом, алгоритмические предписания можно задавать словесным способом, схемой и таблицей.

Действуя с конкретными математическими объектами и обобщениями в виде правил, дети овладевают умением выделять элементарные шаги своих действий и определять их последовательность.

Например, правило проверки сложения можно сформулировать в виде алгоритмического предписания следующим образом. Для того чтобы проверить сложение вычитанием, нужно:

1) из суммы вычесть одно из слагаемых;

2) сравнить полученный результат с другим слагаемым;

3) если полученный результат равен другому слагаемому, то сложение выполнено верно;

4) в противном случае ищи ошибку.

Для формирования умения составлять алгоритмы нужно научить детей: находить общий способ действия; выделять основные, элементарные действия, из которых состоит данное; планировать последовательность выделенных действий; правильно записывать алгоритм.

Рассмотрим задания, цель которых – выявление способа действия:

Даны числа (см. рисунок). Составь выражения и найди их значения. Сколько всего примеров на сложение можно составить? Как нужно рассуждать при этом, чтобы не пропустить ни одного случая?

При выполнении данного задания ученики осознают необходимость выделения общего способа действия. Например, фиксировать первое слагаемое 31, в качестве второго прибавлять все числа второго столбика, затем, в качестве первого слагаемого фиксировать, например, число 41 и опять выбирать все числа из второго столбика, и т.д. Можно фиксировать второе слагаемое и перебирать все числа первого столбика. Важно, чтобы ребёнок понял, что, придерживаясь какого-то определённого способа действия, он не упустит ни одного случая и ни один из случаев не запишет дважды.

В зале три люстры и 6 окон. К празднику для украшения от каждой люстры к каждому окну протянули гирлянду. Сколько всего повесили гирлянд? (При решении можно использовать схематический рисунок.)

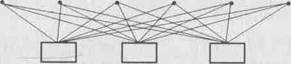
Для формирования у учащихся умения выявлять способ действия полезны комбинаторные задания. Их особенность в том, что они имеют не одно, а множество решений, и при их выполнении необходимо осуществлять перебор в рациональной последовательности. Например:

Сколько различных пятизначных чисел можно записать, используя цифры 55522 (цифру 5 можно повторять три раза, 2 – два раза).

Для решения этой комбинаторной задачи можно воспользоваться построением «дерева возможностей». Выписывается сначала одна цифра, с которой можно начать запись числа. Дальнейший алгоритм действий сводится к записи цифр, которые можно поставить после каждой цифры, пока не получим пятизначное число. Следуя данному алгоритму, необходимо комбинировать и подсчитывать, сколько раз повторились цифры 5 и 2.

Получились «веточки» с различными числами: 55522, 55252, 55225, 52552, 52525, 52255. Затем записывается цифра 2.

Записываем числа, двигаясь по «веточкам»: 22555, 25525, 25552, 25255. Ответ: можно записать 10 чисел.

Программа Петерсон Л. Г.

По данной программе вводится понятие «алгоритм», а также рассматриваются виды алгоритма.

М2П ч.1 с.75

 

М2П ч.2 с.32

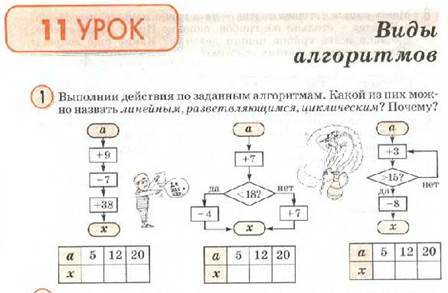
 на страницах учебника рассматриваются следующие алгоритмы:

Например, словесные алгоритмы, типа:

М3П ч.2, с.11

М2П ч.2, с.8

М1П ч.3 с.25

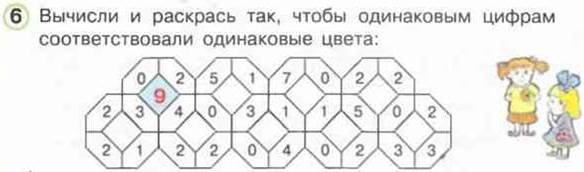
Алгоритмическое предписание:

1) Сложите числа по краям каждой стороны квадрата;

2) Впишите полученный результат в квадрат, стороны которого вы складывали;

3) Раскрасьте квадраты с одинаковыми числами в одинаковые цвета.

 

 

Программа Моро М. И.

По данной программе само понятие «алгоритм» не рассматривается, на страницах учебника даются алгоритмы сложения/ вычитания/ умножения/ деления двузначных/трехзначных/многозначных чисел (Словесные алгоритмы)

Например:

«Сложение двузначных чисел без перехода через разряд»

М2М ч.2 с.4

«Вычитание двузначных чисел без перехода через разряд»

М2М ч.2 с.5

«Деление с остатком»

М3М ч.2, с. 28

«Умножение трехзначного на однозначное»

М3М ч.2 с.89

 

Также, есть задание типа «Вычислительная машина работает так…»

Программа Демидовой Т.Е.

По данной программе рассматриваются понятие «алгоритм», алгоритм с условием

М2Дм ч.3, с.65

М2Дм ч.3, с.68

 

М3Дм ч.2, с. 84

 

5. Опишите методику обучения младших школьников решению комбинаторных задач. Какие способы решения комбинаторных задач вам известны из курса математики? Какими способами решения этих задач могут воспользоваться учащиеся начальных классов? Приведите примеры.  

Обучение решению комбинаторных задач проводится в три этапа:

1. Подготовительный этап, цель которого формирование мыслительных операций в процессе решения комбинаторных задач с помощью хаотического перебора.

На подготовительном этапе предлагаются задачи на развитие познавательных способностей, на активизацию таких мыслительных процессов как анализ, синтез, обобщение и классификация. Это задачи-игры и «жизненные» задачи (задачи, решаемые в повседневной деятельности человека). Например, для обеспечения мотивации решения комбинаторных задач можно предложить детям задачу-игру «День-ночь», «Башенки». Подобные игры с успехом можно проводить во время физминуток.

«Жизненные» задачи», показывающие возможность применения комбинаторики в повседневной деятельности человека также направлены на формирование простых мыслительных операций. Например, интерес у ребят вызывает следующая задача:

«У кассы кинотеатра стоят четверо ребят. У двух из них сторублевые купюры, у других двух – пятидесятирублевые. Как должны расположиться ребята, чтобы никому не пришлось ждать сдачи?» В ходе решения задача обыгрывается: к доске вызываются 4 учеников, получающие модели купюр. Билет в кино стоит 50 рублей. В начале продажи касса пуста. (Вызываю «кассира» и даю ему «билеты»). Находим два возможных варианта решения: 1. – 50 рублей, 100 рублей, 50 рублей, 100 рублей; 2 – 50 рублей, 50 рублей, 100 рублей, 100 рублей. Данные задачи могут предлагаться утомившимся учащимся в конце урока математики.

Таким образом, на подготовительном этапе создается положительная мотивация, происходить эмоциональная подготовка учащихся к дальнейшему решению более сложных комбинаторных задач.

2. Целью второго основного этапа обучения младших школьников решению комбинаторных задач является ознакомление учащихся с новыми видами комбинаторных задач: задачами, решаемыми методом организованного перебора; с помощью таблиц; с помощью графов; с помощью дерева возможных вариантов.

При знакомстве школьников с ходом решения задач методом организационного перебора важно обучить детей выполнять перебор не хаотически, а соблюдая определенную последовательность рассмотрения всех вариантов решений.

Перед тем, как знакомить учащихся с новым способом решения комбинаторных задач – с помощью таблиц, необходимо актуализировать знания детей о таблицах, выделить существенные признаки таблиц и сформулировать определение понятия «таблица», например такое: таблица – это перечень сведений, числовых данных, приведенных в определенную систему и разнесенных по графам (строкам и столбцам).

Примеры задач, решаемых с помощью таблиц:

«Запиши в нужные клетки таблицы следующие числа: 23, 32, 11, 31, 22, 33, 13. Какие числа нужно записать в оставшиеся клетки?»

ед. д.	1	2	3
1
2
3

Перед решением данной задачи необходимо вспомнить с учащимися разрядный состав чисел, используемых в решении задачи.

«Проверь, правильно ли заполнена таблица?»

ед. д.	5	9
2	25	92
7	75	97
1	15	91

 

Как и перед решением предыдущей задачи необходимо вспомнить с учащимися разрядный состав чисел, используемых в решении задачи.

«Для изготовления двуцветных ручек на фабрике использовали красные, желтые, зеленые и синие стержни. Сколько различных видов двуцветных ручек выпускала фабрика? Заполни таблицу и проверь свой ответ. Обведи зеленым цветом клетки таблицы, в которых записаны возможные наборы двуцветных ручек.»

При решении задачи сначала необходимо разгадать правило, по которому составлена таблица и заполнить ее до конца. Составленную таблицу соотнести с условием задачи. Далее обвести зеленым цветом только клетки, в которых показаны ручки разных цветов.

«В одной деревне по сложившейся традиции мужчин называют каким-либо из следующих имен: Иван, Петр, Василий и Михаил. Проживают в этой деревне 15 мужчин. Может ли оказаться так, что в деревне нет мужчин с одинаковым именем и отчеством?»

Для удобства записи данных в таблицу нужно подвести учеников к мысли о том, что имена и отчества можно записывать кратко, используя только первую букву имени и отчества.

 «В танцевальном кружке занимаются пять девочек: Женя, Маша, Катя, Юля и Даша и 5 мальчиков: Олег, Вова, Стас, Андрей и Иван. Сколько различных танцевальных пар можно составить? Заполни таблицу и проверь свой ответ».

Эту задачу предлагаю учащимся в качестве домашнего задания. Таким образом, даю детям возможность самим составить и заполнить таблицу по аналогии.

При решении комбинаторных задач с помощью графов объекты обозначаются точками. Связи между объектами могут обозначаться линиями и стрелками, если нужно показать направление действия или правильную последовательность в изображении объектов.

Новое для школьников понятие «граф» рассматривается на уроке помощью следующей задачи:

«Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий?»

Сначала выясняем с учащимися, как можно обозначить каждого человека (быстрее и удобнее изображать людей точками, которые располагаются примерно по кругу, чтобы записи были понятными и наглядными).

Рукопожатия удобно обозначить черточками. Сначала составить рукопожатия одного человека (точку соединить со всеми остальными), потом перейти к другому человеку. Проведенные линии помогут увидеть, с кем он уже поздоровался, а с кем нет, составить недостающие рукопожатия. Так действовали до тех пор, пока все не поздоровались друг с другом.

Далее учащиеся знакомятся с применением одной из разновидностей графа – деревом возможных вариантов при решении комбинаторных задач.

С детьми выясняем, что данный вид графа, если его перевернуть будет похож на дерево, на котором растут ветки с листьями. Наше дерево отличается тем, что растет сверху вниз, потому что так удобнее располагать объекты в нужной последовательности. Такой вид графа называется деревом возможных вариантов.

Таким образом, на основном этапе дети учатся решать комбинаторные задачи разными способами.

Отработка умения решать комбинаторные задачи логически завершает процесс формирования навыка решения комбинаторных задач в процессе овладения школьниками содержанием начального курса математики. На этапе отработки умений школьникам предлагается решать комбинаторные задачи разными способами (методом организованного перебора, с помощью таблиц, с помощью графов), тем самым, с одной стороны, закрепляя умение решать такие задачи с помощью различных приемов деятельности, с другой – осуществляя действие самоконтроля, являющееся необходимым компонентом учебной деятельности.

Процесс обучения начинается с решения простейших комбинаторных задач, направленных на развитие внимания, наблюдательности, умений анализа, синтеза, сравнения.

К концу обучения в 1 классе учащиеся справляются с решением простых комбинаторных задач способом перебора. Эти задачи развивают наблюдательность, внимание и логическую речь учеников.

Во 2 классе условия задач немного усложняются и требуют от детей внимания, способствуют развитию логического и образного мышления.

В качестве домашнего задания попросить детей попробовать самим составить комбинаторные задачи. Дети составляли их по аналогии с теми, которые решали в классе, например: «Сколько двузначных чисел можно составить из цифр 2,4,0, если цифры не повторяются? Если цифры повторяются?».

В 3 и 4 классах задачи усложняются по содержанию. Они формируют у детей приёмы умственной деятельности, абстрагирования, способствуют развитию произвольного внимания и образного мышления. Дети знакомятся с деревом возможных вариантов, когда способ перебора можно заменить схемой. Схему-дерево возможных вариантов можно располагать по-разному.

Как можно разместить на скамейке Настю, Таню, Мишу и Серёжу, чтобы мальчики и девочки чередовались?

Сначала записываем все возможные варианты расположения детей на скамейке (перебор), потом заменяем схемой.

 

Можно сказать заполнить самостоятельно схему-дерево, если корень дерева расположен вверху.

Такие задачи решить самостоятельно дети затрудняются, поэтому решение задач – коллективное. Составляем таблицу, проводим наблюдения по условию и перебираем варианты.

В учебнике математики за 4 класс более часто встречаются задачи данного вида и решаются они на уроках с подробным разбором.

Большую роль в организации обучения детей решению комбинаторных задач играет процесс дифференциации заданий по уровню сложности. Для учеников, испытывающих особые трудности в решении комбинаторных задач, предлагаются дифференцированные по уровню сложности задания.

1. Сколько четырёхзначных чисел, в которых 6 тысяч, можно записать цифрами 6, 5, 2?

Пониженный уровень: Составить все возможные варианты записи этих чисел.
Повышенный уровень: Заполнить схему-дерево возможных вариантов.

2.В класс пришли четыре новых ученика: Коля, Вася, Саша и Петя. Как учитель может рассадить этих учеников за две свободные парты? Сколько вариантов выбора у него есть?

Пониженный уровень: составить все возможные варианты, пользуясь способом перебора.
Повышенный уровень: Заполнить схему-дерево возможных вариантов.

 

 

Существуют следующие методы решения комбинаторных задач:

Метод перебора (подбираются задачи на развитие мышления)

Табличный метод (здесь все условия вносятся в таблицу, возникает решение)

Дерево вариантов (дети получают начальные знания о графах)

Методы решения комбинаторных задач вводятся по нарастающей траектории от простого к сложному. В 1–2 классе решаются задачи с помощью перебора и таблиц, а в 3–4 с помощью построения дерева вариантов и графов, тем самым позволяя в основной школе при изучении некоторых тем теории вероятности использовать знакомые понятия и способы решения.

Комбинаторные задачи являются средством:

1. Реализации методической концепции, выражающей необходимость целенаправленного и систематического формирования приемов умственной деятельности в процессе усвоения программного содержания.

2. Овладения способом моделирования на доступном для младших школьников уровне.

3. Расширения у учащихся представлений о различных видах математических задач и способах их решения (перебор, таблицы, дерево вариантов)

4. Развития таких свойств мышления как гибкость, вариативность, креативность.

В конце изучения курса математики в начальной школе учащиеся владеют способами решения комбинаторных задач, умеют составлять математически.

Комбинаторные задачи, составленные на жизненном